二维涡旋空间孤子在Kerr型自聚焦介质中的传输及相互作用

李淑青，李 录

（1.太原工业学院 理学系，山西 太原 030008；2.山西大学 物理电子工程学院，山西 太原 030006）

0 引言

当非线性介质的自聚焦效应与光束的衍射发散作用相互平衡时，在介质内无衍射向前传输的光束被称为空间光孤子.近20年来对克尔空间光孤子的研究取得了重大突破，但是克尔空间孤子的形成需要很高的功率，后来人们发现了只需较低功率就可以形成的光折变空间孤子［1-3］.近几年来，涡旋场以其独一无二的特征逐渐被人们所重视，到2009年涡旋空间孤子在实验中被观察到［4-6］.2013年，张解放研究了非线性介质中涡旋孤子的相互作用［7］，之后欧阳世根研究了自散焦介质中涡旋孤子的特性［8］，然而对涡旋空间孤子在克尔性自聚焦介质中的动力学特点，及拓扑荷对涡旋孤子的影响还鲜为人知，因此对涡旋孤子在Kerr型自聚焦介质的动力学研究具有重要的实际意义.

本文对涡旋空间孤子在Kerr自聚焦介质中的演化方程进行了简化，求解了简化后的非线性方程，并导出了振幅的取值范围.采用数值模拟的方法讨论了拓扑荷的值对涡旋孤子的影响，以及拓扑荷和振幅对两涡旋孤子相互作用的影响.

1 二维空间涡旋孤子在Kerr型自聚焦介质中的演化方程

麦克斯韦方程是普遍适用于电磁场和光场中的基本方程.一般情况下，光场中的麦克斯韦方程可以写成下面的波动方程：

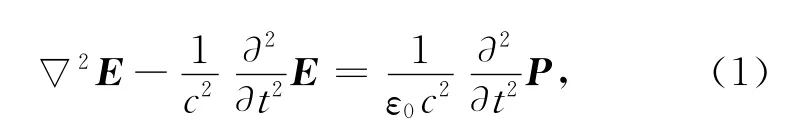
式中：E是电场强度；P是极化矢量；c是真空中的光速；ε0是真空中的介电常数.方程具有E（r，t）＝A（r）exp（iβ0Z）的形式解，其中β0 ＝knn0＝A（X，Y，Z）是演化波包，光沿着Z轴传播，衍射（自聚焦）发生在X，Y轴构成的平面内，在没有衍射和非线性的情况下，A是一个常数.在考虑非线性效应和衍射效应的时候，波包A随着Z变化，并满足非线性方程［9］

在非线性Kerr自聚焦介质中，折射率的改变量满足nnl（I）＝n2I，n2是非线性材料的Kerr系数，对于Kerr自聚焦介质，n2＞0，I是光强，且I＝｜A｜2.引入归一化变量

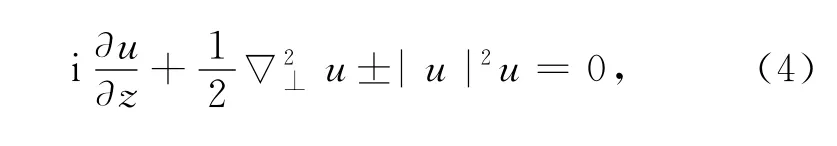
2 二维涡旋孤子解及其特点

关于方程（4）的解R.M.Caplan，Q.E.Hoqb等人已经在2009年求出，形式解可以写成下面的形式［10］：

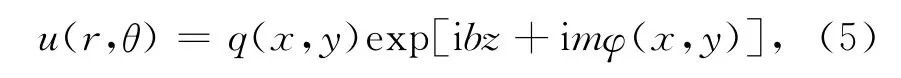
式中：b是演化常数；φ（x，y）为方位角；mφ（x，y）表示横向相位；b是演化常数，一般情况下满足0≤b≤1；m取整数，它满足称为拓扑荷，描述相位绕奇点变化的快慢；q（x，y）为实函数.采用拟解法把方程（5）代入到方程（4）中，即可得到方程（6）.

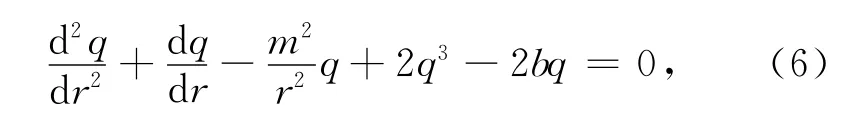
式中：q满足边界条件：q｜r＝0＝0，q｜r→∞＝0，q～r｜m｜（r→0）.为了讨论的一般性，设方程（6）的初始孤子解具有下面的形式：

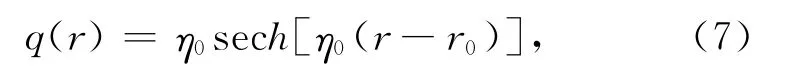
式中：η0表示振幅；r0表示初始时的孤子半径.把上述解代入到方程（6）中，整理后得

根据双曲函数的特性-1＜tanhx＜1，可以得到简化后的参数方程满足

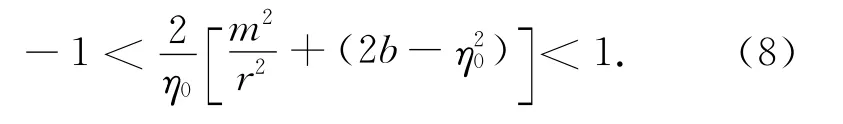
对于不等式（8），尤其当m＝0时即可以求得η0 必须满足方程（9）.

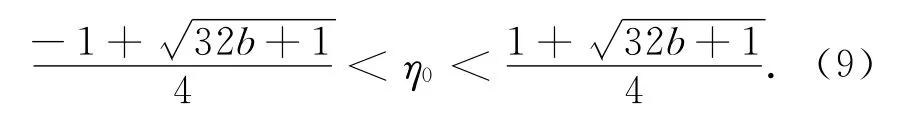
如果m≠0 时，根据η0表示振幅的实际物理意义，可以得到η0 的取值范围为

可见振幅随着拓扑荷与半径的比值变化.

图1 中显示了孤子解

在z＝0，m＝0和m＝±3时的光强分布剖面图，参数为b＝1，r0＝1，η0 ＝1.从图1 中可以看到，当拓扑荷m＝0 的时候，孤子的中心光强最大，就是普通的Kerr 孤子；但是，当拓扑荷m＝±3时，对应的孤子中心光强为零，此时的孤子形成环形涡旋孤子.

图1 x-o-y内孤子的光强图Fig.1 The light intensity of soliton in x-o-y

3 涡旋孤子的传输特点

考虑由硅材料制作的圆形波导，其中：n0＝1.57，表示波导中心光斑通过处的折射率；n1＝1.55，表示波导边缘的折射率.非线性折射率n2＝3 × 10-9m2／W，让 入 射 波 长λ（λ＝512nm）和初始波函数的形式为u（r，θ）＝η0sech［η0（r-r0）］exp（imφ（x，y））的光入射其中，此时光孤子的横向特征长度衍射长度由于方程（4）已经做了归一化处理，因此坐标x，y轴分别以0.2mm 作为单位，z轴以0.7mm 作为单位.孤子的稳定性一直是讨论的重点，那么拓扑荷m对孤子的稳定性有什么影响呢？图2 是在参数满足m＝0，b＝1，r0＝1和η0 ＝0.5，孤子分别在z＝0，z＝75，z＝150时的演化剖面图.从图2 中可以看出，随着孤子的演化，孤子的形状保持不变，但是半径逐渐变小，在孤子传播了150个演化单位时，孤子的形状并没有失真，但是中心光强随距离收缩的很快，说明参数取m＝0时的孤子解不稳定.这种现象归因于在光束的传输过程中，光场强度与自聚焦效应互为因果关系，即光场强度增大会导致自聚焦效应增强，而自聚焦效应增强又会导致光场强度增强，这样自聚焦效应就越来越大于衍射效应，使得光束自囚禁，从而被破坏.

图2 二维涡旋空间孤子传输剖面图（r0＝1，b＝1，η0 ＝0.25，m＝0）Fig.2 The profile of 2Dimensional vortex spatial soliton transmission for different distances（r0＝1，b＝1，η0 ＝0.25，m＝0）

图3显示了拓扑荷取m＝±3，其他参数取r0＝5，b＝1，η0 ＝1时空间涡旋孤子（也就是孤子）分别在z＝0，z＝17.5，z＝35 时传输开始（图3（a）），传输了12.5mm（图3（b））和传输了24.5 mm（图3（c））的演化图.从图中可以看出，m＝±3 的涡旋孤子传输极不稳定，孤子随着传输距离的增加分裂成四孤子团，组成的四个孤子分布在同一个环上，强度分布具有光链的样式，每个波瓣中间都有一个节点，类似于文献［11］中提到的Necklace-ring 涡旋孤子.

图3 x-o-y平面内孤子在不同演化距离时的光强分布（r0＝5，b＝1，η0 ＝1，m＝3）Fig.3 The light intensity of vortex soliton in x-o-yfor different distances（r0＝5，b＝1，η0 ＝1，m＝3）

4 两涡旋孤子的相互作用及其抑制

在文献［7-8］中，作者讨论了涡旋孤子间的相互作用受孤子间距和孤子相位的影响，而且都是针对拓扑荷为2的涡旋孤子进行了讨论，对拓扑荷为其他值及拓扑荷的取值对孤子相互作用的影响没有进行讨论.为了更全面地了解涡旋孤子之间的相互作用，图4 模拟了当两涡旋孤子间的间距为2 mm 时，取不同的拓扑荷m的相互作用图.图4中显示了，当拓扑荷为0时，孤子发生了形变，中心点的光强突然加强，周围的光强突然减弱，已经失去了初始孤子的原貌，可见m＝0时的普通孤子相互作用极不稳定.当｜m｜≥1时，从图5 的（b），（c），（d）中可以看出，随着m的增大，孤子的相互作用增强，孤子相接触的边缘强度增大，这与涡旋孤子的半径随拓扑荷的增大而增大有直接关系，且拓扑荷m＝1 时的涡旋孤子稳定性最高.

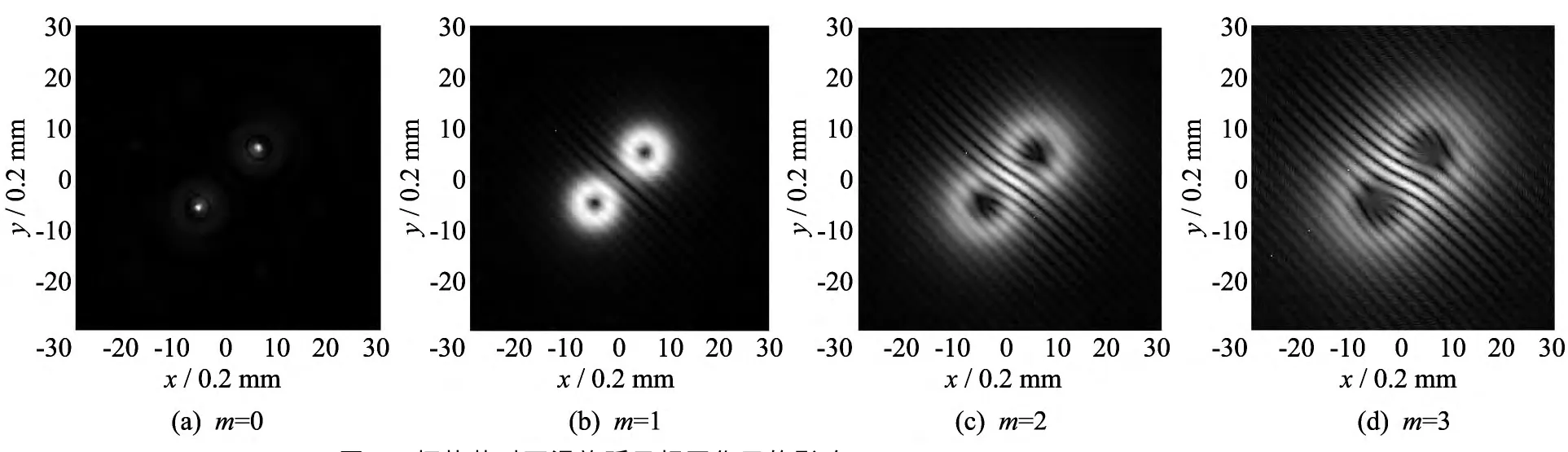
图4 拓扑荷对两涡旋孤子相互作用的影响（r0＝1，b＝1，η0 ＝1，z＝5）Fig.4 The effect of the topological charges to the interaction of two vortex solitons（r0＝1，b＝1，η0 ＝1，z＝5）

作者以拓扑荷值m＝1 为例，研究了振幅对两涡旋孤子相互作用的影响.在一般情况下孤子的相位、振幅比和强度都在一定程度上可以抑制孤子的相互作用，有关相位对孤子相互作用的影响，文献［7-8］中已经讨论过了，这里重点讨论孤子的强度对孤子相互作用的影响.图5 分别显示了当两个涡旋孤子间距为2 mm 时，振幅分别选为η0 ＝0.25，η0 ＝1.5，η0 ＝1.8，η0 ＝1.88，其他参数分别为r0＝1，b＝1，z＝5时的相互作用图.从图5 中和图4（b）这5张图片可以看出，两涡旋孤子的相互作用受振幅的影响很大，当孤子的振幅η0 ＜1.5时，图5（a）和图4（b）所显示的孤子的相互作用较大，孤子的振幅越小孤子的边缘重叠越严重；当孤子的振幅1.5≤η0 ≤1.8时，孤子间的相互作用得到了抑制，孤子无相互作用传输；当孤子的强度η0 ＞1.8时，孤子的相互作用较弱，但是两个涡旋孤子都分裂出了两个旁瓣，出现了失真.可见涡旋孤子的相互作用可以通过调节光孤子的强度来抑制，但是振幅的取值应该有一定的范围，这与本文第2部分讨论的式（10）一致.

图5 振幅对两涡旋孤子相互作用的影响Fig.5 The effect of the amplitude to the interaction of two vortex solitons

5 结论

针对2+1维涡旋空间孤子在Kerr自聚焦介质中的演化进行了讨论，利用拉普拉斯变换简化了演化方程.对它的一种分析解利用拟解法求出了振幅所满足的不等式.用数值模拟的方法分析了拓扑荷的值对涡旋孤子的影响，发现当m＝0时，孤子的形状就是普通的Kerr孤子，孤子在传输时半径随着传输距离的增大均匀地减小，正符合孤子的自相似演化特点.当m＝3时，孤子在相位奇点处振幅为零，变成涡旋孤子，它在传输时分裂成四孤子团.分析了拓扑荷的值和振幅对两相邻涡旋孤子相互作用的影响，发现当m＝1 时孤子的相互作用最弱，并且选择合适的振幅可以抑制涡旋孤子的相互作用.

［1］Towers I，Malomed B A.Stable（2+1）-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity［J］.J.Opt.Soc.Am.B，2002，19：537-543.

［2］Zhao Xuesong，Li Lu，Xu Zhiyong.Dark-soliton stripes on a paraboloidal background in a bulk nonlinear medium［J］.Phys.Rev.A，2009，79：043827.

［3］Li L，Zhao X，Xu Z Y.Dark solitons on an intense parabolic background in nonlinear waveguides［J］.Phys.Rev.A，2008，78：063833.

［4］李海莲，杨德兴，任小元，等.体全息产生光学涡旋的实验研究［J］.光学学报，2010，30（2）：503-507.Li Hailian，Yang Dexing，Ren Xiaoyuan，et al.Experimental investigation of optical vortex Generated by volume holography［J］.Acta Optica Sinica，2010，30（2）：503-507.（in Chinese）

［5］何德，闫红卫，吕百达.厄米高斯涡旋光束形成的合成光涡旋及演化［J］.中国激光，2009，36（8）：2023-2029.He De，Yan Hongwei，Lv Baida.Evolution and composite optical cortices of Hermite Gaussian vortex beams［J］.Chinese J.Lasers，2009，36（8）：2023-2029.（in Chinese）

［6］Rao Lianzhou，Pu Jixiong.Generation of partially coherent vortex bottle beams［J］Chin.Opt.Lett.，2007，5（7）：379-382.

［7］张解放.非均匀非线性波导中涡旋光孤子的相互作用传播［J］.光学学报，2013，33（4）：0419001-1-8.Zhang Jiefang.Interaction propagation of optical vortex solitons in inhomogeneous nonlinear waveguides［J］.Acta.Optica sinica，2013，33（4）：0419001-1-8.（in Chinese）

［8］欧阳世根.自散焦非局域非线性材料中的光学涡旋孤子［J］.物理学报，2013，62（4）：040504-1.Ouyang Shigen.Optical vortex solitons in self-defocusing Kerr-type nonlocal medium［J］.Acta Phys.Sin.，2013，62（4）：040504-1.（in Chinese）

［9］Agrawal G P.Nonlinear Fiber Optics［M］.3rd ed.Academic，San Diego，CA，2001：56.

［10］Caplan R M，Hoqb Q E，Carretero-Gonzalez R，et al.Azimuthal modulation instability of vorieces in the nonlinear Schrodinger equation［J］.Opt.Commun.，2009，282：1399-1405.

［11］Desyatnikov A S，Kivshar Y S.Necklace-ring vector solitons［J］.Phys.Rev.Lett.，2001，87（3）：033901.