利用ARMA模型的直流电机模型的辨识

刘莉欣，曹云峰，庄丽葵，王 彪

(1.南京航空航天大学自动化学院，江苏 南京210016;2.南京航空航天大学 高新技术研究院，江苏南京210016)

四旋翼飞行器是一种具有4个螺旋桨的飞行器，并且4个螺旋桨呈十字形交叉结构，相对的四旋翼具有相同的旋转方向，分2组，2组的旋转方向不同.具有垂直起降稳定悬停和自主巡航能力.与传统的直升机不同，四旋翼直升机能通过改变螺旋桨的速度来实现各种动作.在军事和民事领域具有广阔的应用前景.

微小型四旋翼飞行器的姿态取决于4个直流电机的转速［1］.为了精确控制电机的转速，通常对电机模型的传递函数进行辨识，电机的扭矩和角速度等输出取决于当前输入电压.当然它们的这种相关性取决于电机的电感、电阻、转动惯量以及摩擦因数和载荷等因素.用系统辨识方法确定的传递函数相对比机理建模准确，辨识得到直流电机模型的一种方法是利用递推预报误差方法(RPEM)，该方法利用电压作为输入，位置信息作为输出，有研究者利用一个加有噪声的变化电压作为输入，位置信息作为输出来进行辨识，然而极少能得到准确模型.系统辨识方法也广泛应用于非线性机电一体化系统［2］、异步电机［3］、数控机床［4］和机器人技术［5］方面.本文直流电机模型的辨识将利用脉冲响应来得到输出数据，通过最速下降自回归滑动平均模型算法(ARMA)来将原系统输出角速度和辨识模型的角速度之间的误差降到最小［6］.建立起ARMA模型后通过脉冲响应辨识出系统的Z变换传递函数模型.

1 直流电机模型

对于直流电机，根据机械和电压守恒有以下2个等式:

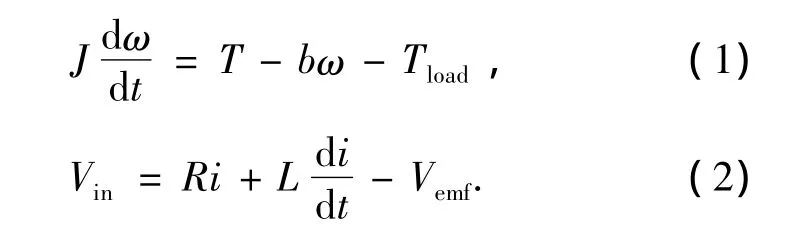
其中T为电机扭矩，Tload为电机载荷扭矩，ω为电机角速度，J为电机转动惯量，b为电机摩擦因数，Vin为电机输入电压值，Vemf为电磁式电压力，i为电机电流，R为电机绕组阻值，L是电机绕组电感.

另外扭矩T和电机当前电流存在比例关系，电磁电压Vemf与电机角速度ω存在比例关系，

其中Km是电机机械常数，Ke为电机电力常数.

另外电机载荷的扭矩可以进一步化成包含载荷转动惯量的形式.

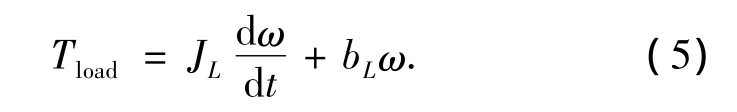
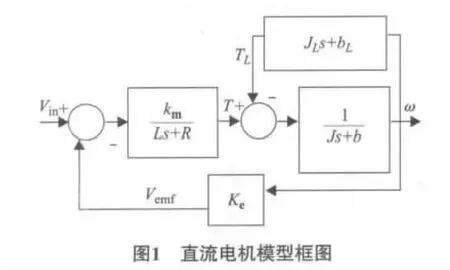
将(3)～(5)式代入(1)、(2)，将输入电压作为输入，电机转速作为输出并且进行拉氏变换，得到电机输入输出模型，如图1所示.

2 ARMA模型和最速下降算法

系统辨识指的是通过实验数据(系统的输入和输出)来确定系统的模型.

在ARMA模型中，假设被辨识的系统满足以下条件:

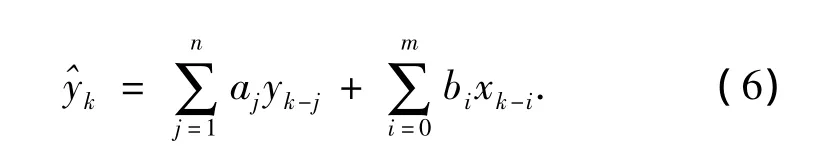
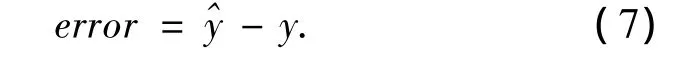
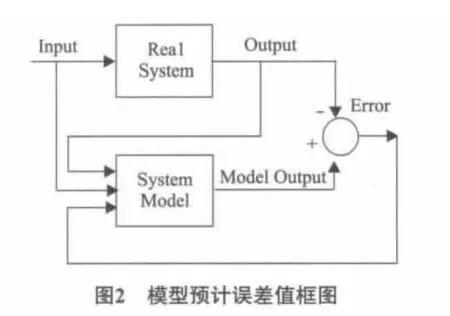
输入输出值可通过待辨识系统的仿真或物理模型的实际测量得到，输入输出在式(6)中用来计算，它们的关系如图2所示，aj和bi随着输入输出的值变化而变化，使得误差最小.

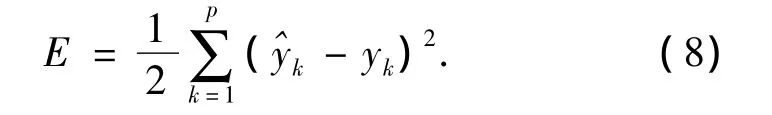
其中p是有效数据采样数，每个序列最小二乘逼近值为:

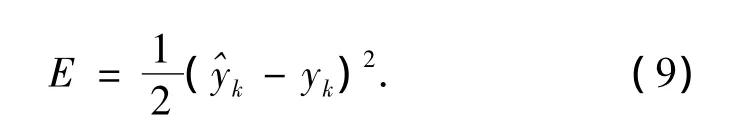
这是我们需要的最小化误差方程.

最速平滑下降算法可以在此处用来计算误差的最小值，通过以下求导可得:

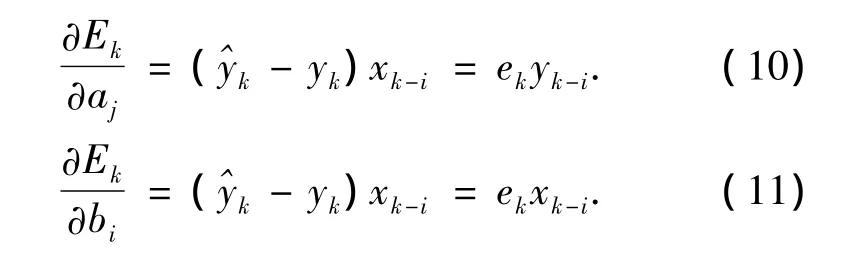
最速下降平滑算法被用来得到以下不断更新的值:

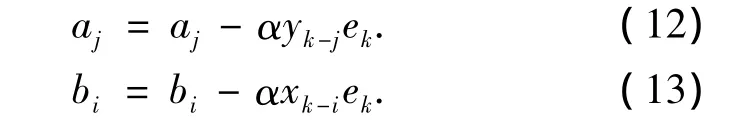
其中α为步长，为了得到最佳步长值，可以利用线性搜索方法，但该方法相对用时较长，参数确定之后，我们就可以利用计算ARMA模型的Z变换来得到待估计模型的传递函数:

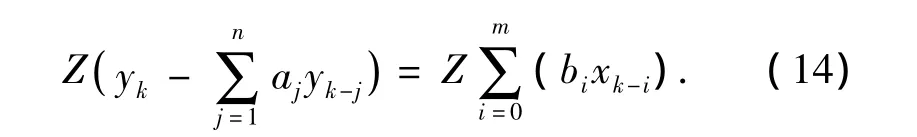
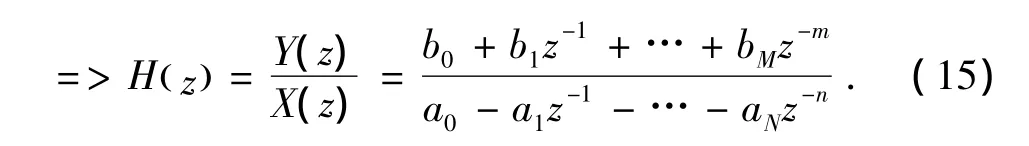
我们知道，当系统的输入为脉冲函数时，系统的输出为y(n)，等于该系统传递函数h(n).因此系统输出的Z变换等于系统传递函数的Z变换值H(z).

3 仿真结果

利用脉冲输入来使得电机模型产生角速度的输出，然后根据已知的输入和电机角速度的输出，利用ARMA算法对模型参数aj和bi进行计算，从而就能得到待辨识的模型.

对实验室飞行器上的电机进行辨识，已知飞行器400个输入数据，400个输出数据，取步长为5×10-7，5 ×10-6，1 ×10-5，辨识模型输入输出如图3 ～5所示，可见步长取5×10-6更加接近电机实际输出模型，步长越小，待辨识模型接近实际模型的速度变慢，而步长过大导致电机待辨识模型噪声过大，最大值与最小值之间差距抖动剧烈，模型结构相对不稳定.因此我们取比较接近实际模型的步长值5×10-6.图6为实际电机模型输出.

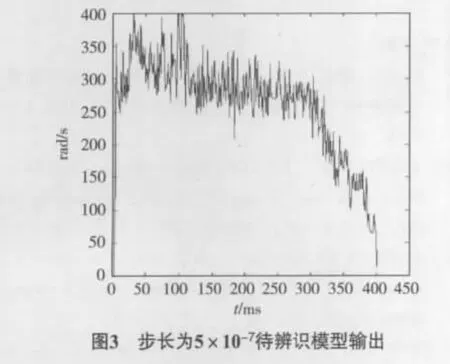
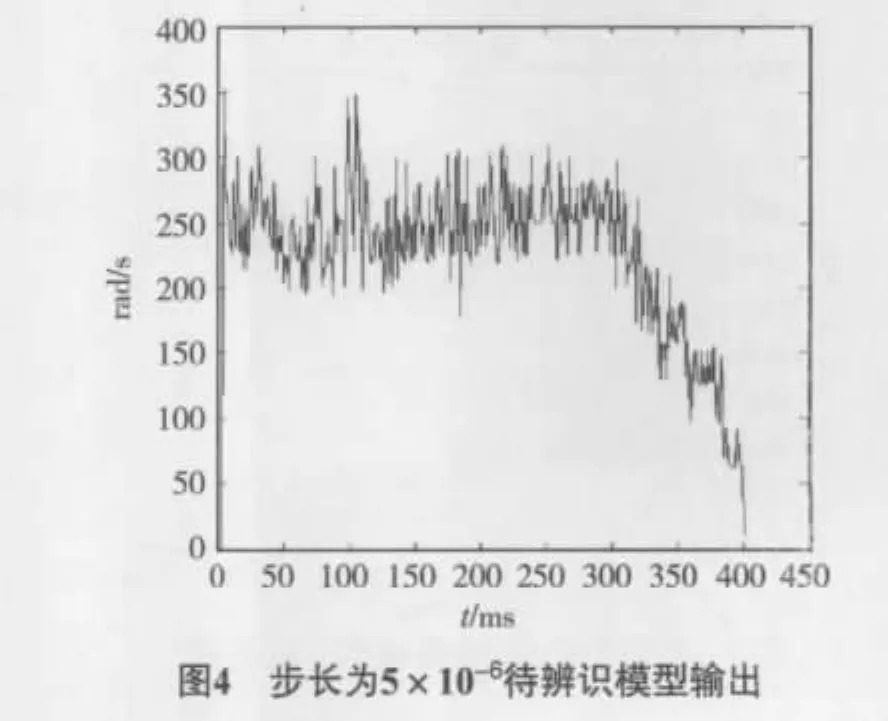
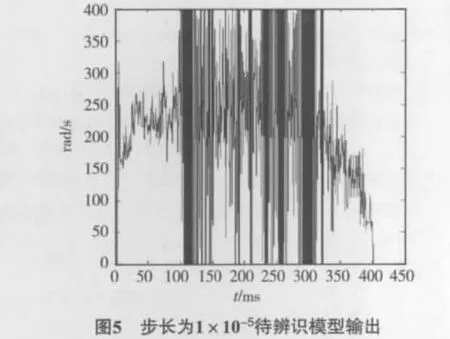
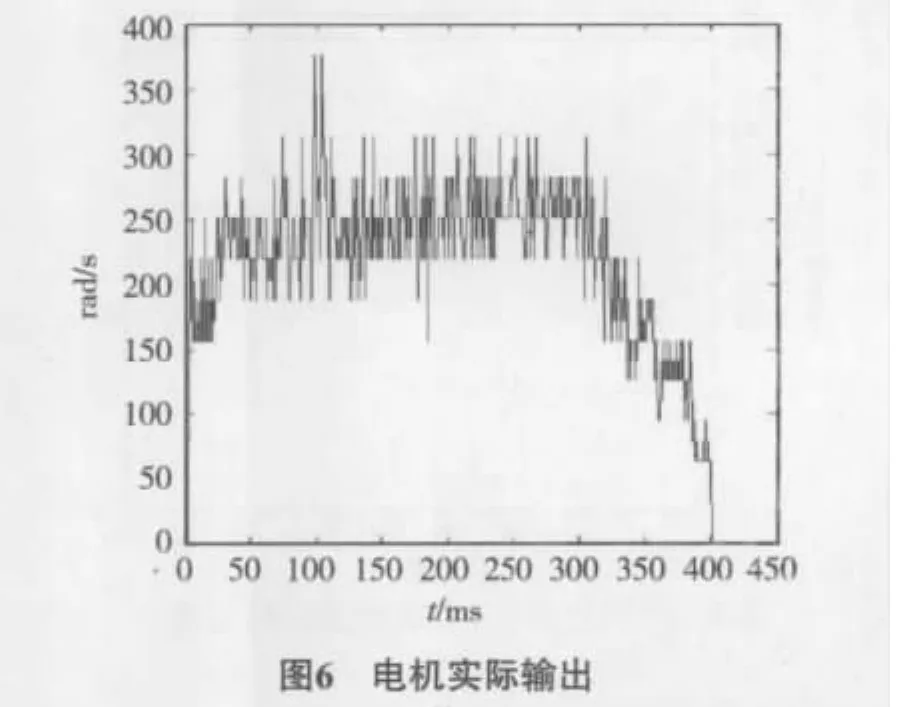
图6与图4很相似，一定程度保证了数据的有效性.通过已知的输入输出和本文第3章介绍的ARMA及最速下降平滑算法，可以计算出aj和bi的值，从而得到系统脉冲传递函数的模型.分别对系统进行3阶、4阶和5阶的脉冲传递函数的计算，结果为

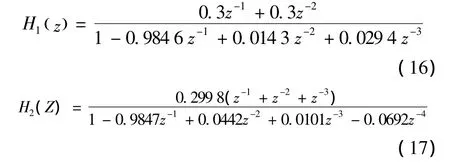
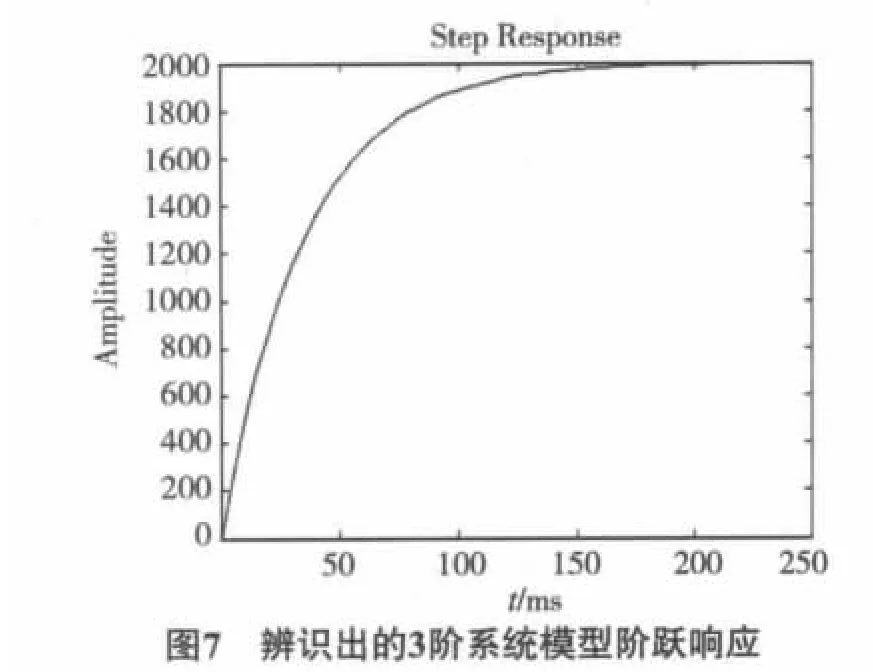
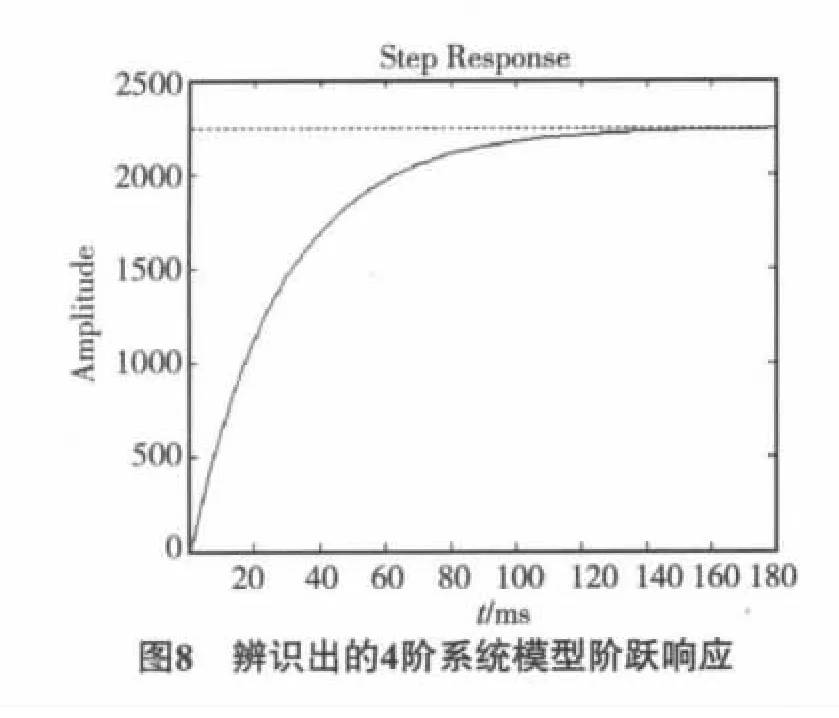
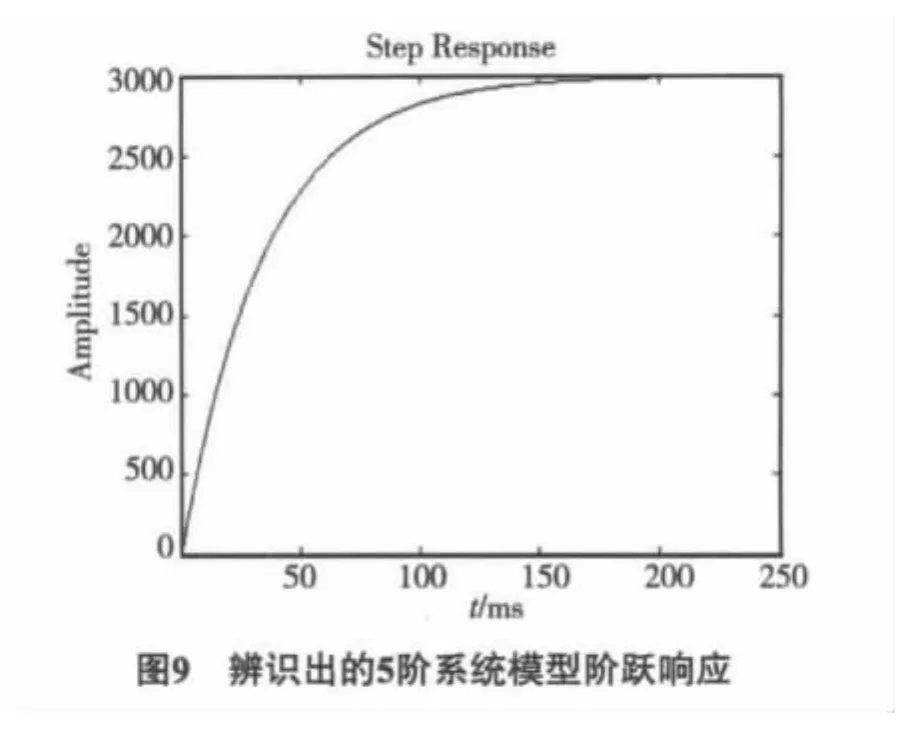
不同阶数脉冲传递函数得到的系统进行阶跃响应，曲线如图7～9所示.

4 结语

阶跃响应输入值为1，而电机采用的输入值为前200个数据是0.15定值，后200个数据是0.图3中可见，前200 ms时系统已达稳定状态，电机输出峰值在300～350 rad/s，部分值接近400 rad/s，我们对辨识出的3阶系统模型进行阶跃输入，可见输出值为2 000左右;对辨识出的4阶系统模型进行阶跃输入，可见输出值为3 000左右;而我们对辨识出的5阶系统模型进行阶跃输入，可见输出值为3 000左右.3阶系统稳定值与电机模型输出输入值相比，比4阶与5阶系统的更接近.可见3阶系统更接近系统真实值.因电机系统本来阶数较小，增大阶数反而引进了不必要的误差，并且阶数越大引入的误差反而越大，未来我们可以对输出信号进行多种阶数的测试，并对电机输出值进行滤波处理，将野值进行剔除，这样所得结果会更准确.

［1］杨成顺，杨忠，张强.一种新型多旋翼飞行器的建模与反演控制［J］.济南大学学报:自然科学版，2013(1):52-58.

［2］ANGERER B T，HINTZ C.Online identification of a nonlinear mechatronic system［J］.Control Engineering Practice，2004，12(11):1465-1478.

［3］KOUBAA Y.Recursive identification of induction motor parameters［J］.Simulation Modelling Practice and Theory，2004，12(5):363-381.

［4］YAN M T，LEE M H，YEN P L.Theory and application of a combined self-tuning adaptive control and crosscoupling control in a retrofit milling machine［J］.Mechatronics，2005，15(2):193-211.

［5］ÖSTRING M，GUNNARSSON S，NORRLÖF M.Closedloop identification of an industrial robot containing flexibilities［J］.Control Engineering Practice，2003，11(3):291-300.

［6］郭永刚，许亮华，水小平.基于脉冲响应数据的ARMA法建模以及模态参数识别［J］.地震工程与工程振动，2006，26(5):167-171.