例谈不同层次学生向量教学的实施策略

叶秋平

(宁德市职业中专学校，福建宁德，352100)

向量是数学地位极其重要的一章，其灵活的变化使得学生对向量的试题往往无从下手。向量试题往往从不同的策略实施下手，代数化策略和图形化策略是最主要的解决策略。笔者发现，成绩较好的学生往往两种策略均能正确掌握，更喜欢图形化策略;对于数学知识能力运用较弱的学生而言，代数化策略是教学的首选，其将向量问题代数化，使得较难的向量问题运用代数的工具进行解决。图形化策略偏重思考、轻运算，代数化策略则恰好反之。

一、多解策略，发散思维

多解策略是解题教学中受教师欢迎的一种策略，该策略注重了学生发散思维的培养，在解决问题的过程中，教师引导学生从不同知识出发，将各种解决手段融合到一起。笔者认为，向量教学中使用这样的方式，既可以围绕向量渗透各种数学基本知识，也能激发学生多思维的策略，对于优等生而言，这是一种极易培养思维发散性、知识整合性的优秀手段。

策略二:既然是代数运算，向量坐标法必定行得通，得出法二:

反思:本题的选择能体现基础与本质的关系，突出了主干，也突出了几何直观。教师先引导学生总结解决此类问题常用的方法:1.坐标法;2.数形结合;3.向量方法的运用。让学生从数学知识整体与方法上全面去认识解题，力求从“一题多解”中学会辨析好与不好的解法，把好方法的选择与解题落实到复习中。以上两种解法从结论出发，执果索因，思路朴实正确;但计算较繁，如果一步出错，满盘皆输。这就对学生的计算能力提出了高要求，做选择题时学生很少能耐着性子算下去。

策略三:对于向量的题目，很多同学还是愿意从向量式的几何意义出发，构建三角形。

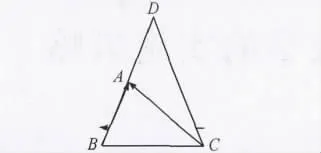
反思:该方法符合学生实际情况，简洁明朗，通俗易懂，将向量问题转化成平面几何问题，计算难度远远小于解法一和二，笔者认为这是本题最好的方法，也是学生最容易想到的方法。

策略四:顺着学生的思路，既然能构建三角形，那么平行四边形中是否也蕴涵着本题的真相。

解法四:通过平行四边形法则及菱形的几何性质得在 Rt△ABC 中，||=|AC|＞|AB|=|+|，故选 C。

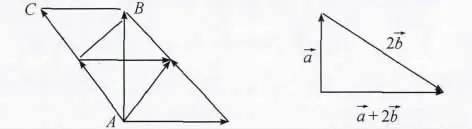
反思:此法还是采用数形结合的思路，有学生想到了此法，上黑板板演，但由于图形相对复杂，学生最终无法解答，主要靠教师讲解分析，学生才勉强接受。此法也让学生重视图形语言，平时多画一些图，既直观又有逻辑，好的数学题都蕴涵着丰富的图形。教师选中此题，可谓用心良苦。当然，要构建直角三角形也可以通过对已知条件的变型，充分发掘题目涵义，如:，则=0，所以如图所示:显然，，此方法体现了数与形的完美结合，值得一提。

策略五:平行四边形是一个重要载体，如果法4的图形有点复杂，巧妙利用一个不等式，很快答案就出来了。

反思:该解法太简洁了，充分体现数形结合的思想，拓展了学生思维。但对于绝对值不等式学生很陌生，很难想到此法。

策略六:本题为模拟试题，参考答案给出了怎样的解法呢?学生很有兴趣知道，故又介绍了第六种解法:

反思:对式子的结构进行变形、拼凑，是学生的一个弱点，此法与解法五一样技巧性太强，不能普及。

策略七:当学生在感叹这么多方法时，(教师接着说:)既然上述方法想不到，对于选择题又有什么特殊的解题技巧呢?

反思:作为教师，我们在处理这样的向量问题时，多一些“一题多解”，少一些“单一重复”，效果会更好。教师应调动学生对向量学习的好奇心，认识数学的奇妙。其实，向量问题是透明的，指向是很明确的。像这样的问题时常出现，它分布在选择题、填空题中，用于考查学生对数学思想方法的理解和运用，通过多样性解决向量问题，开拓优秀学生的解题思路，减少无用功。

二、机械策略，强调运算

向量对于数学能力较弱的学生而言，其对转化、图形等想法较弱，因此教学策略势必向代数化靠拢。代数策略用吴文俊先生的话说，即机械化策略。用机械化策略可以给这些学生一个明确的方向:即少思维、多运算，只要运算细致便能突破向量问题。来看一个代数化案例:

师:本题中我们可以发现题中的几何背景是一个特殊图形:矩形，这样我们就容易想到以矩形的两条相邻直角边作为x轴，y轴建立直角坐标系。这里我们以AB为x轴，AD为y轴建立直角坐标系。(建系)

师:建系后，根据条件分别求出所对应各点的坐 标，A(0，0)，B(，0)，E(，1)，F(x，2)。 (设点)

师:求出各点坐标后，接下来我们把题中的条件进行坐标化，那么我们有·=(，0)·(x，2)=，求出x=1，这样我们就知道了F点的坐标。(条件坐标化)

师:在上述解题过程中，我们根据条件中图形几何的特征建立坐标系，然后设出条件和所求中的点的坐标，通过点的坐标表示出条件和所求，最后通过计算得出答案。上述解题步骤也是利用坐标法解决向量问题的一般步骤，请同学们回想刚才的过程。在这些步骤中，建立坐标系是关键，也是难点。本题坐标系建立比较容易，利用了易知的垂直关系。下面我们来看一道题，请思考本题我们应如何建立坐标系，使我们的解题方便简单。

师:对于本题我们应该如何建立坐标系?在没有现成的图形垂直提示情况下，我们一般应该如何考虑?

生:可以考虑以BC为x轴，过M作BC中垂线为y轴建立坐标系。

师:为什么想到以BC的中垂线为y轴?以其他的为y轴是否可行?

生:以其他的做y轴建立坐标系也是可以的，但是以BC中垂线为y轴，对于下一步求点坐标和条件坐标化的计算有帮助，方便我们计算。

师:想法很正确。和前一题不同，本题没有互相垂直的条件，需要我们自己建立坐标系。通常我们可以从图形对称性等方面尝试建立直角坐标系，这样方便我们的计算。当然有兴趣的同学可以尝试其他的建系方法，如以BC为x轴，过B点做BC垂线为y轴等。

师:下面我们仿照前一题的求解步骤把条件中的点以坐标形式给出:

(可由学生回答)B(－5，0)，M(0，0)，C(5，0)，设A(x，y)，然后把条件坐标化由AM=3得:x2+y2=9，最后得到 和 点积计算可得。

师:本题中我们建系以其中一条已知线段的中垂线做y轴，这样的好处是方便我们的后续求值和计算，这也是我们建系时常见的思考方法。

师:下面给同学们一个思考题，请大家从坐标系的角度去考虑如何求解，加深认知。

说明:对这一内容所选的题目都是经典试题，对程度较弱的学生很有针对性。针对建立坐标系这一难点，3个题目按照由浅入深逐步推进。案例2容易建立坐标系的一个题型，让学生明确抓住图形的几何特征建立坐标系的建系思想;其次让学生感受坐标法的解题过程，明确一般的解题步骤。变式1没有明确的坐标系建系暗示，需要学生自己建立坐标系，这个问题主要是让学生体会恰当建立坐标系可以让解题更加方便，另外也让学生巩固坐标法解题的步骤。最后一问以思考题的形式给出，是坐标法的运用，是对学生在前两例题的基础上的一个提高和自测。对3个题目的处理方式上，案例2主要由教师分析讲解，学生体会。变式1则由学生和教师共同参与，同时教师考查学生的基本认知和掌握情况。思考题则由学生自行解决，是对本方法的课后延伸。

综上，笔者针对不同层次的学生研究了不同的向量问题的解决策略，从上述两个研究案例发现，针对程度较好的学生，教师势必研究向量问题的多样性解决方案。这对于巩固向量的几何本质以及数学思维的培养是有积极作用的。另一方面，笔者也专门就学困生研究了代数化的解决策略。就学生数学能力而言，图形化水准的低下使得这些学生对向量问题的解决方式更倾注于代数化策略。文中案例以层层递进式的不同程度问题展示了向量问题代数化的解决策略，并给出了代数化策略解决的一般性思路。

［1］宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013(5).

［2］方厚石.向量教学诠释思维品质［J］.数学通讯，2014(1).

［3］袁桐.重视“向量方法”［J］.数学教学，2007(9).