基于运动趋势的移动对象位置预测

李雯，夏士雄，刘峰，张磊，袁冠

（1.中国矿业大学 计算机科学与技术学院，江苏 徐州 221116；2.中国煤炭工业协会，北京 100713）

1 引言

移动对象空间定位技术的快速发展极大地推动了基于位置服务的广泛应用，为了使服务具有前瞻性，不仅要对移动对象当前活动的位置进行分析，更要能够对其位置进行预测。移动对象位置预测是一项具有挑战性的工作，主要原因如下：由于GPS等定位设备具有采样盲点，移动对象在封闭空间内的位置信息无法被捕获，造成移动对象轨迹数据的部分缺失，这些缺失的部分往往可能是移动对象活动较为重要的区域，因此，轨迹数据的缺失和不完整，大大增加了移动对象活动的预测难度；移动对象的运动具有不确定性，不同周期内移动对象的活动模式不完全相同；移动对象轨迹的时空信息具有离散性和琐碎性，无法将原始轨迹直接用于移动对象未来位置的预测。

现有的位置预测方法大多在移动对象历史行为模式[1,2]或关联规则[3]的基础上进行位置预测。文献[1]提出基于轨迹模式的位置预测方法WhereNext，考虑移动对象的群体模式，却忽略了对象间的相似性以及相似对象活动模式间的局部匹配性，预测准确性不高。文献[3]使用匹配函数从提取的关联规则中发现最佳规则，进而对位置进行预测。文献[4]中提出HDTP算法考虑移动对象位置的时空信息，使用轨迹常见运动模式对位置进行预测。文献[5]提出 PPM-C算法将移动对象近期活动区域序列与历史活动模式进行完全匹配，发现最长匹配序列，并将匹配序列的后续区域作为未来位置的候选。此外，多种预测模型被应用至位置预测中，例如，贝叶斯网络[6]、马尔可夫[7,8]或隐马尔可夫模型[9]、神经网络方法[10]以及状态预测[11]等方法。文献[12]提出基于对象运动模式预测未来路径和目的地的方法。文献[13]将轨迹定义为移动对象运动时穿过的网格的边的有序集合，在此基础上提出Traj-PrefixSpan算法发现频繁轨迹以及移动对象运动模式，进而进行预测。另外，文献[5,8]中介绍了使用手机基站数据集进行预测的方法，应用熵计算从当前基站到达下一个基站的最大概率上限。

以上文献大多从宏观角度分析移动对象兴趣区域间的转换关系，考虑移动对象兴趣区域间运动的研究不多，这样存在2个问题：1）对象活动模式强调移动对象若干活动间的顺序性，由于运动的不确定性，距离较近的区域间的访问顺序可能不固定；2）在移动对象历史活动记录中，一个兴趣区域之后的候选访问区域可能包含多个，仅依靠兴趣区域间的历史访问习惯很难准确地筛选最佳兴趣区域。

本文提出一种基于运动趋势的移动对象位置预测算法(LP-MT,location prediction algorithm based on movement tendency)，使用基于马尔可夫的移动对象活动模型记录相邻访问区域间的转换关系，在保证区域访问有序性的同时，有效地摆脱对传统模式匹配的依赖，降低运动不确定性带来的影响。另外，由于对象从同一兴趣区域出发，至不同区域间的运动路径不可能完全相同，有各自的运动特征，因此移动对象的运动趋势对位置预测具有指导意义。以往算法仅将历史记录中最近停留区域后的已访问区域作为预测的候选，本文将移动对象的所有历史停留区域作为未来位置的候选，并根据位置的特征，将算法结果分为预测位置和推荐位置。真实数据的实验表明，算法可以对移动对象未来位置进行有效、高效的预测，较同类算法相比，预测精度提高10%左右。

2 基于运动趋势的移动对象位置预测模型

基于运动趋势的移动对象位置预测算法（LP-MT）包括移动对象历史活动模型的训练以及未来位置的预测2个阶段。

在训练阶段（如图 1所示），对移动对象历史活动模式进行学习。首先，采用文献[14]中介绍的基于时间距离约束的网格聚类算法，从原始轨迹中提取历史停留区域集合，集合中的停留位置将作为未来位置的候选，该集合称为潜在停留区域集合（图1中潜在停留区域集合为{A,B,C,D}）。其次，移动对象历史轨迹被表示为潜在停留区域的序列（如图 1 中A-＞B-＞C-＞A-＞B-＞D-＞A），序列反映了移动对象的历史活动模式，访问顺序以及访问次数反映了移动对象运动的规律以及对各区域的喜好程度。最后，以潜在停留区域序列为输入，建立基于马尔可夫的移动对象活动模型。

图1 LP-MT算法训练阶段示意

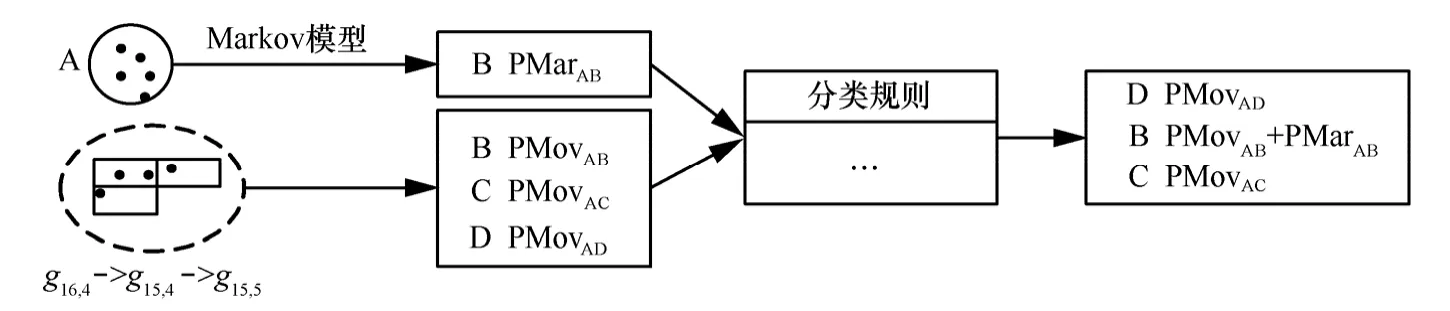
图2 LP-MT算法预测阶段示意

未来位置预测过程（如图2所示）中，首先将移动对象最近停留区域结合基于马尔可夫的移动对象活动模型进行初步预测。其次，将最近停留区域至当前位置间的轨迹段对应至停留区域提取时划分的网格中，将轨迹点序列转换为网格序列（如图 2中g16,4-＞g15,4-＞g15,5），使用网格序列中提取的移动对象运动特征描述移动对象的近期运动趋势，根据运动趋势对移动对象未来位置进行进一步的预测。最后，根据未来位置的分类规则，给出综合预测结果。

2.1 基于移动对象活动模型的预测

目前，移动对象未来位置预测算法大多通过挖掘移动对象轨迹的频繁模式来发现其历史停留区域间的关联关系。在现实世界中，部分停留区域可能较为集中，移动对象对这些区域的访问顺序有很大的随机性。假设3个停留区域A、B、C间的距离较小，D、E为距离A、B、C较远的2个区域，移动对象历史活动模式中包含以下序列：A-＞B-＞C-＞D，A-＞B-＞C-＞E，B-＞A-C-＞E，B-＞C-＞A-＞D。若移动对象的近期停留区域序列为B-＞A-＞C，完全匹配历史活动模式时，预测结果为E。然而，A、B、C间的距离较近，区域访问具有不确定性，因此D作为未来停留区域的概率也较大。另外，对象近期停留区域序列的长度很难选取。本文借鉴马尔可夫模型的思想，提出基于马尔可夫的移动对象活动模型，考虑相邻停留区域间的转换，对移动对象历史活动建模。

马尔可夫模型[15]由一系列状态以及状态转移矩阵组成，第n次转换获得的状态只和第n-1次的状态有关。移动对象的历史停留区域序列SRL={SR1,SR2,…,SRN}可以被表示为状态变量序列XL={X1,X2,…,XN}。若移动对象潜在停留区域的数量为m，则状态空间集合EL=＜E1,E2,…,Em＞，每个停留区域对应一个状态，移动对象在某一时刻只能处于一种状态。根据移动对象的当前状态以及状态间转移关系，可以粗略估计移动对象的后续状态。

若移动对象最近停留区域为SRr，历史记录中区域 SRr后已访问的停留区域集合为SRLN={SRl1,SRl2,…,S Rls}，SRr和SRli是移动对象连续访问区域，SRli称为SRr的后续停留区域，本文将移动对象最近停留区域的后续停留区域集合 SRLN称为预测停留区域集合。最近停留区域SRr在状态空间集合中的对应状态为Er，Er的后续状态集合为ELN={El1,El2,…,Els}。状态 Er至后续状态 Eli的一步转移概率 PMarr,li=P(Er→Eli)=P(Xn+1=Eli|Xn=Er)体现了停留区域 SRli作为停留区域SRr的未来位置的可能性。预测停留区域集合 SRLN中的区域作为最近停留区域SRr的未来位置的概率集合PMarL={PMarr,l1,P Marr,l2,… PMarr,ls}。

2.2 基于移动对象运动趋势的预测

移动对象活动模型从停留区域的角度对移动对象活动习惯进行描述，而对象近期运动趋势也能够指导移动对象未来位置的预测。例如，对象从停留区域A出发可能到达B和C，但B、C分别在区域A的左侧和右侧。若对象从A出发向左走，距离B越来越近，则尽管历史记录中到达C的概率较大，根据移动对象的近期运动趋势可以发现，B更可能为移动对象的未来停留位置。因此本文在考虑停留区域间关系的同时，也考虑移动对象的近期运动趋势，使用移动对象运动方向以及与各潜在停留区域的距离对移动对象运动趋势进行描述。

移动对象轨迹中距离当前时间越近的信息越能反映移动对象的近期运动趋势，对预测结果的影响越大。本文将移动对象最近停留区域至当前位置间的轨迹段转换为网格序列，首先计算网格序列至各潜在停留区域的距离概率和方向概率，然后根据距离权重和方向权重得到综合概率，用来描述运动趋势对各潜在停留区域作为未来位置的影响。

1)至潜在停留区域的距离概率

从宏观角度，移动对象至目标位置的距离应越来越短。本文认为移动对象趋向于向距离当前位置较近的停留区域运动，若一段时间内，移动对象距离区域X越来越近，则移动对象下一个停留区域为X的概率较大。为了将距离标准转换为概率，假设当前网格到各潜在停留区域的最远、最近距离分别为Dmax、Dmin，到达X的距离为DX，则从当前网格到达 X 的概率为Pd(X)=1−(DX−Dmin)/(Dmax−Dmin)。网格序列GL={G1,G2,…,Gs}至潜在停留区域X的距离概率集合为PLd={Pd1(X),Pd2(X),…,Pds(X)},则网格序列至X的综合距离概率为

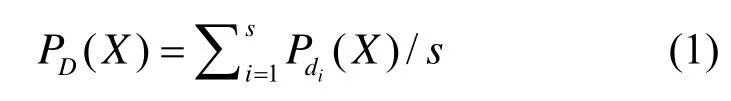
2)至潜在停留区域的方向概率

移动对象向目标位置移动过程中，整体行进方向会趋向于目标位置的方向。当前网格与前一网格以及停留区域代表网格间都存在方向向量。若随对象运动、方向向量间夹角越来越小，则停留区域为目标位置的概率较大。假设当前网格的第一个样本点为pi+1，前一网格中最后一个样本点为pi，则方向向量，区域 X代表网格的中心点为r'=(x,y)，则当前网格至X的方向向量为，当前网格至区域X的方向概率为Pa(X)=cos。网格序列 GL=＜G1,G2,…,Gs＞至区域 X的方向概率集合为PLa=＜Pa1(X),Pa2(X),…,Pas(X))＞，则网格序列至X的综合方向概率为

若综合距离概率和综合方向概率的权重分别为WD和WA，则网格序列至X的综合概率

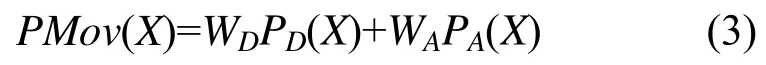
假设移动对象潜在停留区域集合为SRL={SR1,SR2,…,SRm}，反映移动对象近期运动趋势的网格序列GL=＜G1,G2,…,Gs＞，则根据网格序列计算至潜在停留区域集合 SRL中的各个区域的综合概率集合PMovL={PMov1,PMov2,…,PMovm}。

2.3 移动对象未来位置的分类

移动对象未来位置可以分为三类：一是预测停留区域集合中的位置，即历史数据中记录的最近停留区域的后继停留区域；二是潜在停留区域集合中预测停留区域外的其余停留区域，这类区域单纯依靠轨迹模式是无法得到的；最后一类是移动对象未出现过的区域，这类区域无法通过单个对象的历史数据得到，需要分析和当前对象相似的多个对象才能给出合适的结果。本文只考虑前两类位置，即预测位置和推荐位置。

移动对象可能在其历史停留区域集合中的任意位置停留，因此潜在停留区域集合中的区域将作为未来位置的候选。潜在停留区域 X作为移动对象未来位置的可能性大小被定义为区域 X的可达性，表示为PRX。若一段时间内，移动对象到达停留区域 X的可达性都较高，则移动对象运动到区域X的可能性最大。

针对预测位置和推荐位置，LP-MT算法得到预测区域可达性列表和推荐区域可达性列表。预测区域可达性列表对应上述第一类，包含预测区域列表以及各个区域的可达性，其中预测区域列表按照区域可达性递减的顺序排列。通过基于马尔可夫的移动对象活动模型和运动趋势的综合计算可得到预测区域的可达性。推荐区域可达性列表为上述第二类位置，包含推荐区域列表以及各个区域的可达性，其中推荐区域列表按照区域可达性递减的顺序排列。推荐区域的可达性可通过对移动对象近期运动趋势的分析得到。

若移动对象最近停留区域SRr与基于马尔可夫的移动对象活动模型匹配得到的移动对象预测停留区域的概率集合为PMarL={PMarl1,PMarl2,…,PMarls}，根据移动对象近期运动趋势得到的所有潜在停留区域的综合概率集合 PMovL={PMov1,PMov2,…,PMovm}。预测区域列表由预测停留区域集合组成，预测区域可达性列表的概率集合为PRLPre={PRl1,P Rl2,…,P Rls}，其中 PRli=PMarli+PMovli,PRli＞PRli+1,i∈{1,s} 。推荐区域可达性列表集合为SRLCom={SRj| SRj∈SRL∧SRj∉SRLN}，列表中的区域按照可达性递减的顺序排列，区域 SRj的可达性为PRj=PMovj，PRj＞PRj+1。

3 基于运动趋势的移动对象位置预测算法

3.1 算法描述

LP-MT包含2个阶段：1）训练阶段，移动对象历史数据作为训练数据集，提取历史停留区域及历史活动序列，并以此建立基于马尔可夫的移动对象活动模型；2）预测阶段，根据移动对象最近停留区域以及运动趋势进行分步预测。

LP-MT 算法 输入：TTrain(训练轨迹)，TTest(测试轨迹)，Dth(最小距离阈值)，Tth(最小时间阈值)，GHorGVer(网格数量)，WD(距离权重)，WA(方向权重)

输出：SRLPre(预测可达性列表)，SRLCom(推荐可达性列表）

/*训练阶段*/

1)SR=FindStayRegions(TTrain,Dth,Tth,GHor×GVer); /*发现停留区域集合*/

2)SRL=ExtractActivitiesList(SR); /*提取历史活动序列*/

3)MarkovM=BuildMarkovModel(SRL); /*建立基于马尔可夫的移动对象活动模型*//*预测阶段*/

4)SRr=FindRecentSR(TTest,Dth,Tth,GHor×GVer);/*发现移动对象最近停留区域*/

5)GL=AbstractGridsList(TTest,SRr,GHor×GVer);/*提取反映运动趋势的网格序列*/

6)PMarL=CalPredReachList(SRr,MarkovM);/*计算至预测停留区域的概率集合*/

7)PL=CalSynP(GL,SRL ,Wd,Wa); /*计算至潜在停留区域的概率集合*/

8)PMovL=CalPontitalReachList(PL,SRL); /*计算至潜在停留区域可达性*/

9)SRLPre=SynPreReachList(PMarL,PMovL);/*预测可达性列表*/

SRLCom=SynCommReachList(PMovL); /*推荐可达性列表*/

3.2 算法性能分析

LP-MT算法时间主要消耗在移动对象历史活动的发现以及基于对象运动趋势的预测上。历史活动模式发现的时间复杂度为O(n)，n为移动对象训练轨迹样本点数量。利用运动趋势进行预测的时间复杂度为O(ms)，其中m为移动对象历史停留区域的数量，s为最近停留区域至当前位置的网格数量。为确保算法具有较高的时间效率，当真实停留区域确定后，可以对活动模型进行调整和更新。当预测次数小于对象活动模型最大更新上限时，历史活动模式重建的时间被更新对象活动模型的时间代替，对象活动模型更新的时间复杂度为O(m)。

4 实验及分析

为了验证本文提出的基于运动趋势的移动对象位置预测算法，采用Visual C# 2005开发了移动对象未来位置预测系统 LP-MT，轨迹数据存储在SQLServer 2000中。实验进行的软硬件环境包括：Windows XP，Lenovo ThinkCentre (Duro 2，2.8G的CPU，3G内存)。实验数据集使用2007年希腊雅典市区卡车(Trucks)的运动轨迹[16]。

4.1 参数影响

本实验测试网格数量对于基于马尔可夫的移动对象活动模型的健壮性的影响，选取Trucks数据集中ID=900的轨迹进行实验，设定最小距离阈值Dth=400 m，最小时间阈值Tth=5 min，由于对象运动时对方向和距离的无意识性，设定 WD=WA=0.5。图3显示不同网格数量和训练集规模时，马尔可夫模型状态数、网格序列数以及运行时间的变化情况。

通过图3可以看出，基于马尔可夫的对象活动模型的状态数随着网格数量增加而增加，相同网格大小，不同数据样本规模时，对象活动模型的状态数增势平缓；另外，预测时间随网格数量增加略微增加，但增速缓慢。以轨迹10%的数据量为梯度，选择数据量的30%～80%作为预测模型的训练样本，进行6次未来位置的预测。当网格数量为10×10时，共计产生 3次推荐和 3次预测，预测准确率为100%。3次推荐中，真实停留区域分别位于推荐区域可达性列表的1、2、2位，此时状态数较少，因此实验结果较理想。网格数量为30×25时共产生4次预测和2次推荐。4次预测中实际停留区域分别位于预测区域可达性列表的 1、1、2、4位，推荐中实际位置分别位于推荐区域可达性列表的 3、4位。网格数量增加并没有使预测准确率增加，主要原因是：虽然网格数量增加使得对象活动模型更加健壮，但是精细划分的网格使得原本联系紧密的状态被分割，对象很小的动作被分离出来，增加预测误差。而且反映对象运动趋势的网格序列至潜在停留区域的距离以及偏转趋势受网格数量的影响，很小的距离或方向偏差可能对预测结果有很大影响。因此，网格大小的选择应该适中。

图3 不同网格数量和数据规模对LP-MT算法的影响

4.2 预测精度

为了检验预测精度，本文采用增量验证方式，选取Trucks数据集中ID=870的轨迹进行分组实验。为了衡量基于运动趋势的移动对象位置预测算法的准确性，给出评价预测精度的预测准确率和推荐准确率、预测误差率和推荐误差率2组概念。假定预测次数为N，真实停留区域位于预测可达性列表首位的次数为PN，则预测准确率PAPre=PN/N。同理，假设真实停留区域位于推荐可达性列表首位的次数为RN，则推荐准确率 PACom=RN/N。假设移动对象当前位置至真实停留区域的距离为Dc-r，预测位置至真实停留区域的距离为Dp-r，则预测误差率PFPre=Dp-r/Dc-r。同理，若推荐位置至真实停留区域的距离为Drec-r，则推荐误差率PFCom=Drec-r/Dc-r。当前位置至真实停留区域的距离越大，预测产生误差的概率越大，因此根据Dc-r与Dp-r的比值来衡量算法的误差率比较合理。预测误差率或推荐误差率越小，则预测位置或推荐位置越接近真实位置，算法精度越高。

1)不同训练样本比例

该实验主要用于测试在历史数据充分学习的情况下，算法的预测精度。选取整条轨迹30%～85%的数据量作为训练样本，训练样本的结束点作为移动对象的当前位置开始预测。

从表1可以看出，训练样本比例与马尔可夫模型状态数成正比。实验表明马尔可夫模型中10%～20%的状态有3个及3个以上的转换状态，20%～30%的状态有2个转换状态，其余包含一个转换状态，极少数情况下，不包含转换状态，此时，移动对象首次到达该停留区域且没有移动至下一区域。使用不同数据集建立的马尔可夫模型的状态转换情况有所不同。

表1 Truck数据不同训练样本比例对马尔可夫模型状态数量的影响

算法结果由预测可达性列表以及推荐可达性列表共同决定。预测中无法判断真实停留区域位于哪类结果中，因此预测误差率和推荐误差率的最小值决定了算法的综合误差率。图4描述了不同训练样本比例下误差率的变化情况，从图中的曲线可以看出，算法综合误差率基本在0.1以下，预测精度较高。

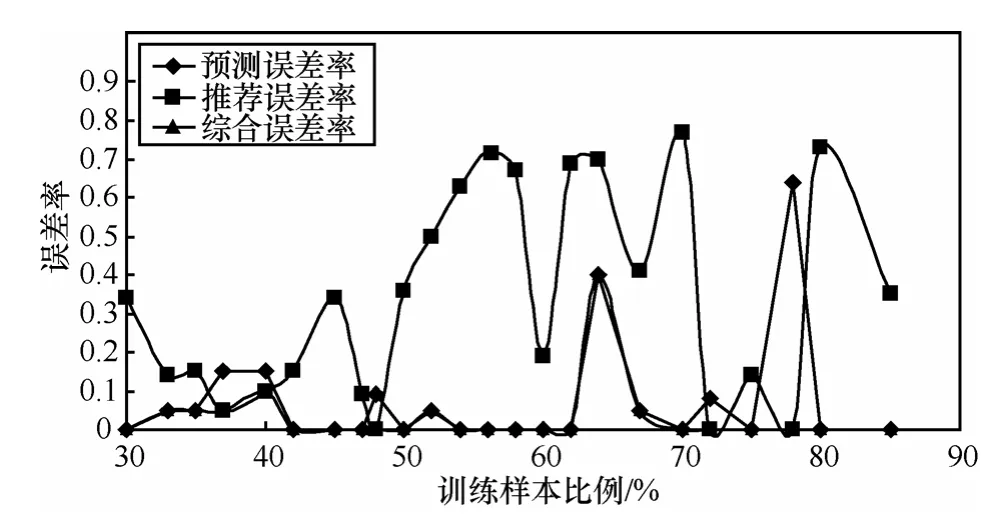
图4 不同训练样本比例下的误差率

以3%的数据集为一个梯度，25次实验中共产生5次推荐和20次预测。推荐准确率达到40%。20次预测结果中，仅根据基于马尔可夫的移动对象活动模型预测的准确率达到50%。增加考虑移动对象运动趋势可提高 24%的预测成功率，其余情况下，结合运动趋势也可以使准确率在简单的一步预测的基础上有显著提高。实验表明算法在不同训练样本比例下都具有较高准确性。

2)训练集规模

该实验主要测试当历史数据量较少时，预测结果的准确性。选取整条轨迹 30%～90%间不同梯度的数据量作为训练样本，以90%处的样本点作为移动对象当前位置。

从图5中的曲线可以看出，训练集规模较小时，推荐结果的准确率较高，这是由于此时移动对象历史数据较少，仅依靠历史停留区域间的转换关系无法准确预测，但是移动对象近期运动趋势能够反映对象活动意图，从而提高推荐准确性。图5显示推荐误差率趋近于 0，表明本文选取距离和方向作为反映运动趋势的标准较为合理。随着训练集规模的增加，预测结果更加准确，综合误差率基本小于0.3。因此，历史数据量较少时，运动趋势能够很好地对未来位置进行推荐，随着历史数据集规模的增大，预测精度则越来越高。

3)学习充分性

该实验用于检验基于马尔可夫的移动对象活动模型能否充分学习对象的历史活动模式。选取整条轨迹50%～100%之间的数据进行训练，从轨迹的45%处开始预测。以5%的数据集为一个梯度，20次实验的预测误差率全部为0，实验表明对象活动模型能够准确、全面地反映移动对象的历史活动模式。

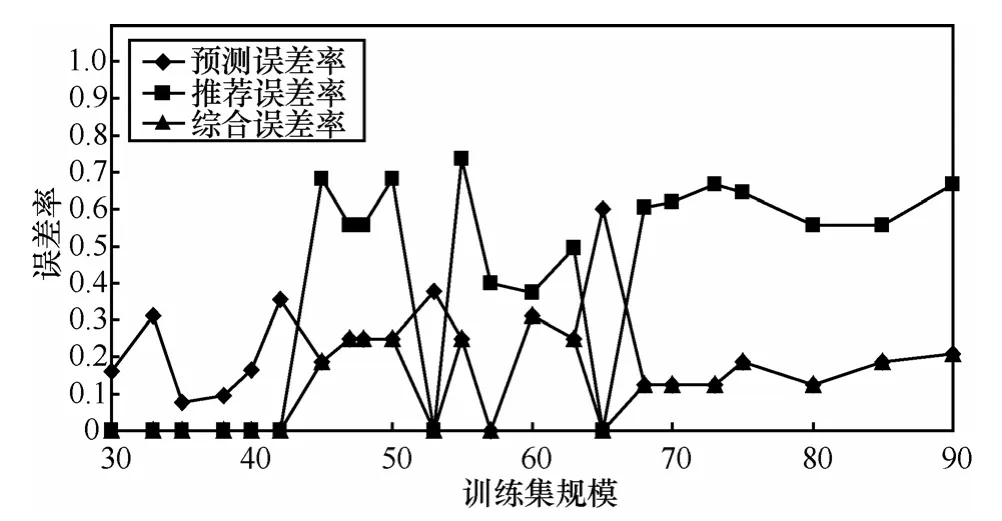
图5 训练集规模与误差率间关系

4)算法稳定性

该实验主要用于测试算法的稳定性。选取整条轨迹为训练集，从轨迹的 30%～90%之间随机选取若干位置作为移动对象的当前位置开始预测。若随机选取一系列位置，误差率集合PFL={PF1,PF2,…,PFn}，则∀1≤i≤n，第 i次预测的平均误差率为。平均误差率反映了算法在多次预测中的持续预测能力，体现了算法的稳定性。图6显示算法的平均综合误差率维持在0.1以下，预测精度较高且较为稳定。另外，对于不同的数据集都有较好的效果，算法的适应性和可移植性较强。

图6 测试位置与平均误差率的关系

4.3 移动对象活动模型的更新有效性

该实验主要测试算法更新的有效性以及最大的更新次数。以50%的数据量为训练数据集对移动对象位置开始连续预测，根据真实停留区域对对象活动模型进行 55次更新。在实际情况中，移动对象的真实停留区域会与历史停留区域有一定的偏差，但如果重叠面积较大，本文认为是同一个停留区域。从图7中的曲线可以看出，前20次更新中，综合误差率基本在0.2以下波动，为可接受的误差范围。然而，在20次更新之后，算法的综合误差率开始增加，甚至达到 0.5。多次更新过程中，移动对象在同一区域出现的位置可能发生变化。因此，更新策略可保证算法在一定次数内的更新是有效的。本实验环境下，20次更新后需要对对象活动进行重新建模。

图7 马尔可夫模型的更新对误差率的影响

4.4 同类算法性能比较

PPM-C算法与LP-MT算法都是对移动对象位置进行预测的方法，在同类算法中，PPM-C算法的性能较好，具有一定代表性。为了比较 LP-MT算法与 PPM-C算法的性能，本文选取整条轨迹数据量的 30%～90%作为训练样本，以 90%处的样本点作为预测起始位置。图8和图9显示与PPM-C算法相比，LP-MT具有较好的预测效果和运行速度。

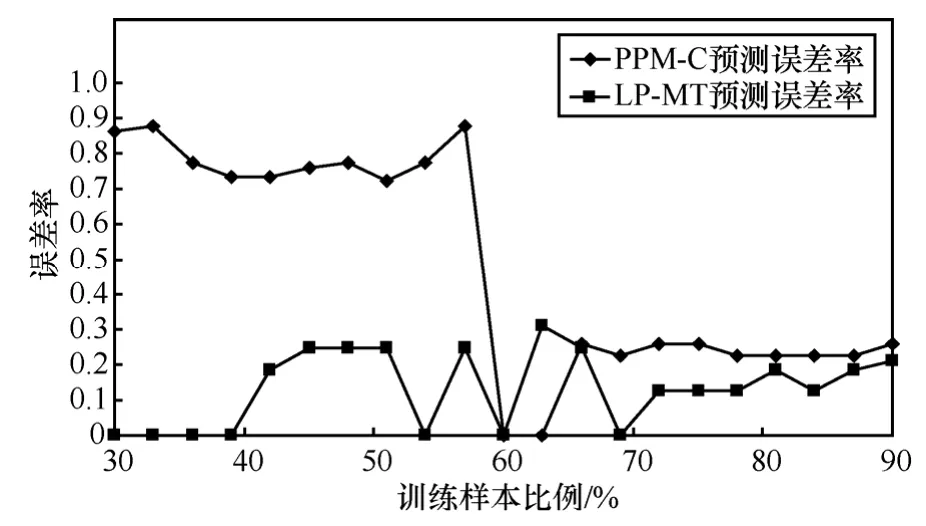
图8 PPM-C与LP-MT算法误差率比较

图9 PPM-C与LP-MT算法运行时间比较

图8比较了LP-MT与PPM-C使用相同训练集，从同一位置开始预测的综合误差率。当训练样本规模占数据集总量的30%～60%时，PPM-C算法的综合误差率基本在0.7以上，同等情况下，LP-MT算法的综合误差率小于0.3。训练样本规模大于数据集总量的70%时，2种算法的综合误差率均小于0.3，LP-MT算法的综合误差率略低。主要由于：1）PPM-C主要依靠学习历史数据来对移动对象未来位置进行预测，当训练样本较小时，PPM-C对历史活动学习不够充分，无法得到较为准确的预测结果，而LP-MT算法在学习不充分时，使用移动对象近期运动趋势对结果进行补充，确保算法具有较好的预测效果；2）PPM-C仅考虑历史数据中最近停留区域的后继停留区域集合，忽略了移动对象运动的不确定性，LP-MT算法在考虑预测停留区域的同时，计算至所有潜在停留区域的可达性，提高预测精度。

图9比较了LP-MT与PPM-C算法的运行时间，PPM-C算法的运行时间随训练样本规模的增大迅速增加，而LP-MT算法的运行时间变化较为平缓。若移动对象潜在停留区域的数量为n，停留区域序列的长度为N(N＞＞n)，PPM-C算法中order表的规模与N成正比，随着训练样本规模的增加，order表的规模迅速增加，而LP-MT只需根据 n个历史停留区域集合进行建模。另外，每次预测时，PPM-C算法依次缩短近期停留区域序列与order表中各层进行完全匹配，使得预测时间较长。因此，训练样本规模较大时，PPM-C算法的运行时间远远大于LP-MT算法的运行时间。

5 结束语

针对目前移动对象位置预测大多只考虑移动对象历史活动模式，导致预测精度不高且预测结果较为局限的问题，提出一种基于运动趋势的移动对象位置预测算法，不仅使用移动对象最近停留区域和移动对象活动模型中存储的移动对象历史活动模式进行匹配给出初步预测，还综合考虑移动对象最近运动趋势，估计各潜在停留区域作为未来位置的概率。根据移动对象未来位置的特征，将潜在停留区域分为预测停留区域以及非预测停留区域，分别对应预测位置和推荐位置。应用真实数据的实验表明，与其他同类算法相比，LP-MT算法预测精度提高近10%。在保证较高时间效率的同时，具有较好的准确性。下一步将在本文研究的基础上，考虑移动对象的群体性以及多移动对象的局部相似性，使用多个对象的轨迹数据对未来位置进行预测。

[1]MONREALE A,PINELLI F,TRASARTI R. Where next: a location predictor on trajectory pattern mining[A]. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C]. New York,2009. 637-646.

[2]YOON H,SHAHABI C. Robust time-referenced segmentation of moving object trajectories[A]. ICDM '08,Eighth IEEE International Conference on Data Mining[C]. 2008. 1121-1126.

[3]MORZY M. Mining frequent trajectories of moving objects for location prediction[A]. Machine Learning and Data Mining in Pattern Recognition[C]. 2007. 667-680.

[4]LI H Y,TANG C J,QIAO S J. Hotspot district trajectory prediction[A]. Web-Age Information Management[C]. 2010. 74-84.

[5]BURBEY I E. Predicting Future Locations and Arrival Times of Individuals[D]. Virginia: Virginia Polytechnic Institute and State University,2011.

[6]PETZOLD J,PIETZOWSKI A,BAGCI F,et al. Prediction of indoor movements using Bayesian networks[A]. Lecture Notes in Computer Science[C]. 2005. 173-184.

[7]彭曲,丁治明,郭黎敏. 基于马尔可夫链的轨迹预测[J]. 计算机科学,2010,37(8): 189-193.PENG Q,DING Z M,GUO L M. Prediction of trajectory based on Markov chains[J]. Computer Science,2010,37(8):189-193.

[8]SONG C M,QU Z H,BLUMM N. Limits of predictability in human mobility[J]. Science,2010,327(5968): 1018-1021.

[9]JEUNG H,SHEN H T,ZHOU X F. Mining trajectory patterns using hidden Markov models[A]. Data Warehousing and Knowledge Discovery[C]. 2009. 470-480.

[10]KOSKELA T,LEHTOKANGAS M,SAARINEN J. Time series prediction with multilayer perceptron,FIR and Elman neural networks[A].Proceedings of the World Congress on Neural Networks[C]. 1996.491-496.

[11]BAGCI P J,TRUMLER F,et al. Global state context prediction techniques applied to a smart office building[A]. The Communication Networks and Distributed Systems Modeling and Simulation Conference[C]. San Diego,2004.

[12]CHEN L,LV M Q,CHEN G C. A system for destination and future route prediction based on trajectory mining [J]. Pervasive and Mobile Computing,2010,6(6): 657-676.

[13]ASHBROOK D,STARNER T. Using GPS to learn significant locations and predict movement across multiple users[J]. Personal and Ubiquitous Computing,2003,(7): 275-286.

[14]ZHENG V W C,ZHENG Y,XIE X. Collaborative location and activity recommendations With GPS history data[A]. Proceeding of International Conference on World Wide Web[C]. 2010. 1029-1038.

[15]http://en.wikipedia.org/wiki/Markov_model[EB/OL]. 2011.

[16]http://www.chorochronos.org/Default.aspx?tabid=75 [EB/OL]. 2012.