带消息填充的29步SM3算法原根和伪碰撞攻击

王高丽，申延召

（1.东华大学 计算机科学与技术学院，上海 201620；2.中国科学院 信息工程研究所 信息安全国家重点实验室，北京 100093）

1 引言

杂凑函数在密码学中具有重要的地位，安全的杂凑函数能够抵抗碰撞攻击、原根攻击和第二原根攻击等。对于杂凑函数的攻击方法有很多，例如基于模差分的碰撞攻击[1,2]方法、基于中间相遇攻击[3]的原根攻击[4]方法等。对于杂凑函数的攻击中最为显著的是王小云等学者提出的对于MD5和SHA-1等国际通用杂凑函数的碰撞攻击[1,2]。随着MD5和SHA-1被破解[1,2]，美国国家标准与技术研究所(NIST)于 2007年启动了新的杂凑函数标准 SHA-3的征集活动[5]，并于2012年10月公布了新一代杂凑函数标准——Keccak算法。

随着SHA-3征集活动的进行，各国都在制定自己的杂凑算法标准。2010年中国国家密码管理局公布了中国商用密码杂凑算法标准——SM3密码杂凑函数[6]。该算法由王小云等学者设计，消息分组长度为512 bit，输出杂凑值长度为256 bit，采用Merkle-Damgard结构。就压缩函数而言，SM3密码杂凑函数与SHA-256具有相似的结构，但是SM3算法的压缩函数的每一步都使用2个消息字，每一步的扩散能力更强。

文献[7]首次给出了对于缩减频数的 SM3算法的原根攻击。其中，对于从第1步开始的28步SM3算法的原根攻击的时间复杂度为2241.5；对于从第7步开始的30步SM3算法的原根攻击的时间复杂度为2249。因为前16步 SM3算法中的函数 FF(·)和 GG(·)均为异或函数，其性质不利于分析的进行，所以文献[7]用到了第 16步以后的函数 FF(·)和 GG(·)的性质，因此，对于 30步 SM3算法的原根攻击不能从第1步开始。文献[8]给出了对于35步SM3算法的飞来去器攻击，其时间复杂度为2117.1，证明了从第1步开始的35步SM3算法是非随机的。文献[9]使用差分—中间相遇攻击给出了对29步、30步、31步和32步SM3算法的原根攻击和伪碰撞攻击，均从第1步开始。但是，文献[9]在构造差分特征时用到了消息填充所需的消息字，因此文献[9]的攻击不能包含有效的消息填充。

在深入分析 SM3算法的特点后，本文提出了一种带消息填充的、从第1步开始的29步SM3算法的原根攻击和伪碰撞攻击方法。本文采用中间相遇技术进行原根攻击，且攻击过程不依赖于 SM3算法中函数 FF(·)和 GG(·)的性质，另外，对于 29步SM3算法的原根攻击可以转化为对于29步SM3算法的伪碰撞攻击。带消息填充的、从第1步开始的29步SM3的原根攻击和伪碰撞攻击的时间复杂度分别为2254和2125。

2 SM3算法

SM3算法将长度为l(l＜264)的消息 M(比特串)进行压缩，输出256 bit的杂凑值。对于消息M，SM3算法首先执行一个消息填充过程，在M 后添加 1个“1”和k个“0”，再添加上64 bit l的二进制表示，k为等式l+k+65≡448mod512的最小正整数解。这样把M填充成长度为512倍数的新消息M'。接着将 M'按照 512 bit进行分组，假定 M'=(B(0),B(1),…,B(n−1))，CF(·)为SM3 算法的压缩函数，则 M杂凑值的计算过程如下

其中，IV为初始值，Vn为M的杂凑值。SM3算法的压缩函数 Vi=CF(Vi−1,B(i−1))由消息扩展过程和变量更新过程组成。

2.1 消息扩展过程

SM3算法的消息扩展过程首先将 B(i−1)分成 16个长度为32 bit的消息字wi，0≤i≤15，然后将其扩展成 68个消息字 wi(0≤i≤67)和 64个消息字wi'(0≤i≤63)。具体过程如下。

i从 16～67:

i从 0～63:

wi'=wi⊕wi+4

其中，P1(X)=X⊕(X＜＜＜15)⊕(X＜＜＜23)。

2.2 变量更新过程

对于给定的初始值 IV=(A0,B0,C0,D0,E0,F0,G0,H0)，SM3算法变量更新的具体过程如下。

对于i从0～63:

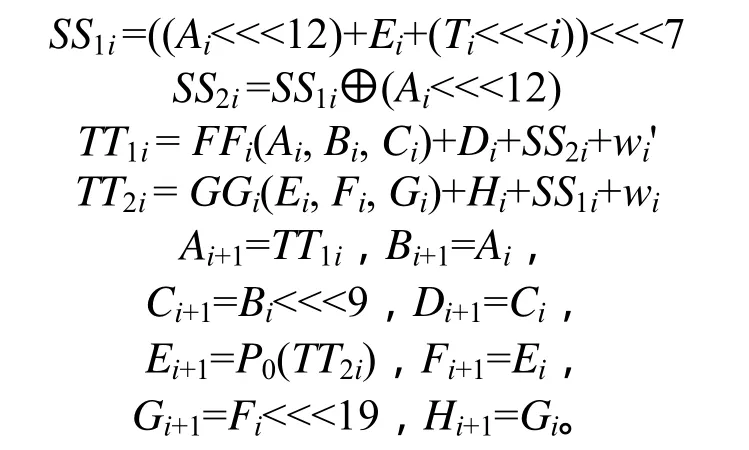
其中，P0(X)=X⊕(X＜＜＜9)⊕(X＜＜＜17)。

FFi(Ai,Bi,Ci)和GGi(Ei,Fi,Gi)的定义如下

2.3 符号说明

以下对本文所使用的符号进行说明。

1)(Ai,Bi,Ci,Di,Ei,Fi,Gi,Hi)表示第 i−1 步的输出变量值。特别地，(A0,B0,C0,D0,E0,F0,G0,H0)表示压缩函数的初始值。

2)pi[a～b]表示32 bit字pi的第a比特到第b比特的值，pi可以为Ai，Bi，Ci，Di，Ei，Fi，Gi，Hi，wi或wi'，0≤a≤b≤31，第0比特为最低位，第31比特为最高位。

3)h=(A,B,C,D,E,F,G,H)表示 256 bit的杂凑值。

4)pi[a～b,c～d]表示 32 比特字 pi的第 a 比特到第b比特和第c比特到第d比特，pi可以为A，B，C，D，E，F，G，H，Ai，Bi，Ci，Di，Ei，Fi，Gi，Hi，wi或 wi'，0≤a≤b≤c≤d≤31。

3 相关技术介绍

3.1 中间相遇攻击

中间相遇攻击由文献[3]提出，文献[4]第一次将中间相遇攻击用于原根攻击，图 1展示了文献[9]中的中间相遇攻击过程，其具体描述如下。

1)选择中立的消息字wf和wb，将压缩函数分为cf和cb两部分，使cf不依赖于wb,cb不依赖于wf。

3)对于所有的 wf，向后计算至相遇点，保存相遇点的变量值，记为Lf。类似地，对于所有的wb，向前计算至相遇点，保存相遇点的变量值，记为Lb。

4)重复步骤2)和步骤3)，直到一个完全匹配产生为止。

图1 中间相遇攻击示意

3.2 伪原根转化为原根

给定压缩值h，若能找到(IV',M')，使得在初始值IV'下压缩M'得到压缩值h，则称M'为h的伪原根，其中，IV'不等于标准初始值IV。文献[10]提出一种将伪原根攻击转化成原根攻击的方法，其基本过程如下：假设杂凑值的长度为n，伪原根攻击的复杂度为2k，一方面，在标准初始值IV下压缩2(n+k)/2个随机的消息，另一方面，计算出压缩值h的2(n−k)/2个伪原根，根据生日攻击可知，中间相遇的期望值的个数是2(n+k)/2×2(n−k)/2/2n=1，从而找到原根的计算复杂度为2(n+k)/2+2(n−k)/2×2k=2(n+k)/2+1次杂凑运算。

3.3 伪原根转化为伪碰撞

记杂凑函数为H，如果能找到(IV,IV',M,M')，使得 H(IV,M)=H(IV',M')，其中，(IV,M)≠(IV',M')，则称找到了杂凑函数 H的伪碰撞。伪原根转化成伪碰撞[11]的方法可以概括为：对于一个输出长度为n的杂凑函数，假定存在一个复杂度为2k、部分匹配为t bit的伪原根攻击，并且部分匹配位于压缩函数的最后一步的输出。对于给定的杂凑值，使用伪原根攻击的方法找到 2(n−t)/2个不同的 t bit部分匹配消息，则根据生日攻击的原理，这些消息以很高的概率存在一个伪碰撞。此时，得到一个伪碰撞所需的复杂度为2(n−t)/2×2k。例如，令部分匹配长度t=6，向前向后计算的过程各进行25次，这样可以得到24(=25+5/26)个6 bit的部分匹配，也就是说，得到一个 6 bit的部分匹配所需的复杂度为2(=25/24)，从而得到一个伪碰撞所需的复杂度为2(n−6)/2×2。

4 29步SM3算法的原根攻击和伪碰撞攻击

对于从第1步开始的29步SM3算法进行原根攻击时，向后的计算过程从第15步到第29步，向前的计算过程从第14步到第1步，这种分割方法使得中间相遇攻击中的部分匹配能够在第 29步进行，从而保证伪碰撞攻击顺利进行，也为中间消息字的选取提供参考。中立的消息字为wb=w13[26～31]，wf=w2[26～31]，这样选择中立消息字的优点在于使抵消中立消息字的条件相对较少，同时这些条件不影响消息的填充过程。其中，在向前的计算过程中，wf=w2[26～31]未知；在向后的计算过程中，wb=w13[26～31]未知。

4.1 设置消息字

根据消息拓展过程可知，w16～w29的拓展过程如下

由上述拓展过程可知，1)从w16～w29首先受到w2影响的消息字为w18，另一方面，在向前的计算过程中，从第14步到第4步不受w2的影响；2)受w13影响的消息字为w16、w19、w22、w26和 w29(w16～w29)，可以通过以下的条件来抵消w13对w16、w19、w22和w26的影响。

由于事故车转弯半径过小，经测量，其弦高h无法准确读出两位有效数字，故使用侧滑速度与车辆碰撞固定物相结合的公式来计算事故车发生侧滑前的行驶速度。

抵消w13对w26的影响。

由于 w26=P1(w10⊕w17⊕(w23＜＜＜15))⊕(w13＜＜＜7)⊕w20，首先用 w10抵消 w13对 w26的影响，需要增加条件

由条件(1)可知w10受到w13的影响，又根据w23的表达式可知，w23受到w13的影响，笔者用条件(2)抵消w13对w23的影响，即

类似地，根据 w20和 w17的表达式可知：w20和 w17受到w13的影响，笔者用条件(3)和条件(4)抵消w20和 w17受到的影响，即

综上可知：w14～w28中除w16、w19和w22之外，其他消息字均不受w13的影响。

抵消w13对w22、w19和w16的影响。根据w22=P1(w6⊕w13⊕(w19＜＜＜15))⊕(w9＜＜＜7)⊕w16，w19=P1(w3⊕w10⊕(w16＜＜＜15))⊕(w6＜＜＜7)⊕ w13，w16=P1(w0⊕w7⊕(w13＜＜＜15))⊕(w3＜＜＜7)⊕ w10，首先用条件(5)抵消w13对w22的影响。

然后用条件(6)抵消w13对w19的影响。

由前面的分析可知：w16表达式中的w3、w7和w10均受到 w13的影响，所以用条件(7)抵消 w13对w16的影响。

综上可知：通过条件(1)到条件(7)对 w0、w1、w3、w4、w6、w7和 w10进行了设定，使得 w14～w28均不受w13的影响。因此，在向后的计算过程中，从第15步到第25步不受w13的影响。其中，C1，…，C7为常数。

4.2 第14步到第1步的计算

因为在向前的计算过程中，w2[26～31]未知，根据消息扩展算法可知，w16和w17已知，w18未知，从而wi和wi'已知(i=3,…,13）,故从分割处的中间变量值(A14,B14,C14,D14,E14,F14,G14,H14)向前逆向计算，可以很容易得到(A3,B3,C3,D3,E3,F3,G3,H3)。由此再向前的计算受w2的影响，其过程如下。首先考虑

由于w2参与此步的运算，且w2[26～31]未知，故可以计算出 A2,B2,C2，D2[0～25],E2,F2,G2和H2[0～25]。然后考虑

根据 SM3算法，易知：A1、B1、C1[0～25]、D1[0～25]、E1、F1、G1[0～25]和 H1[0～25]能够计算出来。最后考虑

根据 SM3 算法，易知：A0、B0[0～16,23～31]、C0[0～25]、D0[0～16]、E0、F0[0～6,13～31]、G0[0～25]和H0[0～6]能够计算出来。

4.3 第15步到第29步的计算

因为在向后的计算过程中，w13[26～31]未知，根据 4.1节消息字的设置可得，wi和 wi'已知(i=14,…,24)，故从分割处的中间变量值(A14,B14,C14,D14,E14,F14,G14,H14)向后计算，很容易得到(A25,B25,C25,D25,E25,F25,G25,H25)的值。

因为参与第26步计算的消息字为w25和w25'=w25⊕w29，而 w29受 w13的影响，所以 A26受 w13的影响，而(B26,C26,D26,E26,F26,G26,H26)不受w13的影响。特别地，E26不受w13的影响，亦即可以得到E26的值，从而根据 SM3算法可知：H29=G28=F27＜＜＜19=E26＜＜＜19 可以计算出来。

综合第14步到第1步的计算过程和第14步到第 29步的计算过程，可以得到部分匹配的检测条件为H0[0～6]⊕H29[0～6]=H[0～6]是否成立。

4.4 29步SM3算法的原根攻击

通过以上的分析可知，为了保证w13对w16、w19、w22和w26不产生影响，需要限定7个消息字w0、w1、w3、w4、w6、w7和w10的条件，一共224(=7×32)bit。对于一个消息分组来说，消息字剩余的自由度为276(=512–224–2×6)，进一步考虑消息填充过程中用到的w13的第0位，w14和w15共65 bit，最终剩余的消息字的自由度为211(=276–65)。另一方面，中间变量(A14,B14,C14,D14,E14,F14,G14,H14)没有任何条件限制，因此可以增加256个自由度，从而可用的自由度为467(=211+256)＞256。显然有足够的自由度来构造出一个有效的对29步SM3算法的伪原根攻击。对于给定的杂凑值h=(A,B,C,D,E,F,G,H)，29步的SM3算法的伪原根攻击过程如下。

1)随机选取中间变量(A14,B14,C14,D14,E14,F14,G14,H14)。对于消息字w0～w15，随机赋值给除w2[26～31]和 w13[26～31]之外的其他消息字，使得 4.1节的条件(1)～条件(7)满足，且消息填充满足。

2)对于所有的 w13[26～31]，向前计算得(A3,B3,C3,D3,E3,F3,G3,H3)。用(w2∧03ffffff)代替 w2向前计算得 (A0,B0,C0,D0,E0,F0,G0,H0)。保存(A3,B3,C3,D3,E3,F3,G3,H3,H0,w13[26～31])到列表Lb中。

3)对于所有的 w2[26～31]，向后计算得 (A25,B25,C25,D25,E25,F25,G25,H25)。在第26步，计算E26的值。保存(A25,B25,C25,D25,E25,F25,G25,H25,E26＜＜＜19,w2[26～31])到列表 Lf中。

4)判断 H0[0～6]⊕H29[0～6]是否等于 H[0～6]。若相等，则使用相应的(A3,B3,C3,D3,E3,F3,G3,H3)和w2[26～31]向前计算得(A0,B0,C0,D0,E0,F0,G0,H0)；使用相应的(A25,B25,C25,D25,E25,F25,G25,H25)和w13[26～31]向后计算得(A29,B29,C29,D29,E29,F29,G29,H29)。

5)判断(A0,B0,C0,D0,E0,F0,G0,H0)⊕(A29,B29,C29,D29,E29,F29,G29,H29)是否等于h。若相等，则相应的消息分组(w0,…,w15)即为29步 SM3算法的一个伪原根。若不相等，则重复步骤1)～步骤4)，直到找到一个29步SM3的伪原根。

上述攻击的时间复杂度估计如下：由步骤2)和步骤3)可知，共有26×26=212个组合，而步骤4)“中间相遇”的概率是 2−7，故做一次步骤2)和步骤3)可以得到 212−7=25个“中间相遇”，而做一次步骤2)和步骤3)的复杂度约为26次29步SM3算法压缩操作，故得到 7 bit“中间相遇”值的复杂度是26/25=2。从而29步SM3算法的伪原根攻击的复杂度为2256−7×2=2250。

使用伪原根攻击转化原根攻击的方法(见 3.2节)，可以得到对29步SM3算法的原根攻击，其时间复杂度为2254(=2256+250)/2+1)。

4.5 29步SM3算法的伪碰撞攻击

根据伪原根攻击转化为伪碰撞攻击的方法(见3.3节)，为了提高效率，把伪原根攻击中部分匹配的判断条件改为H0[0～5]⊕H29[0～5]是否等于 H[0～5]，可以得到29步SM3算法的伪碰撞攻击，其时间复杂度为2125=2(256−6)/2×20，具体 SM3算法的攻击结果如表1所示。

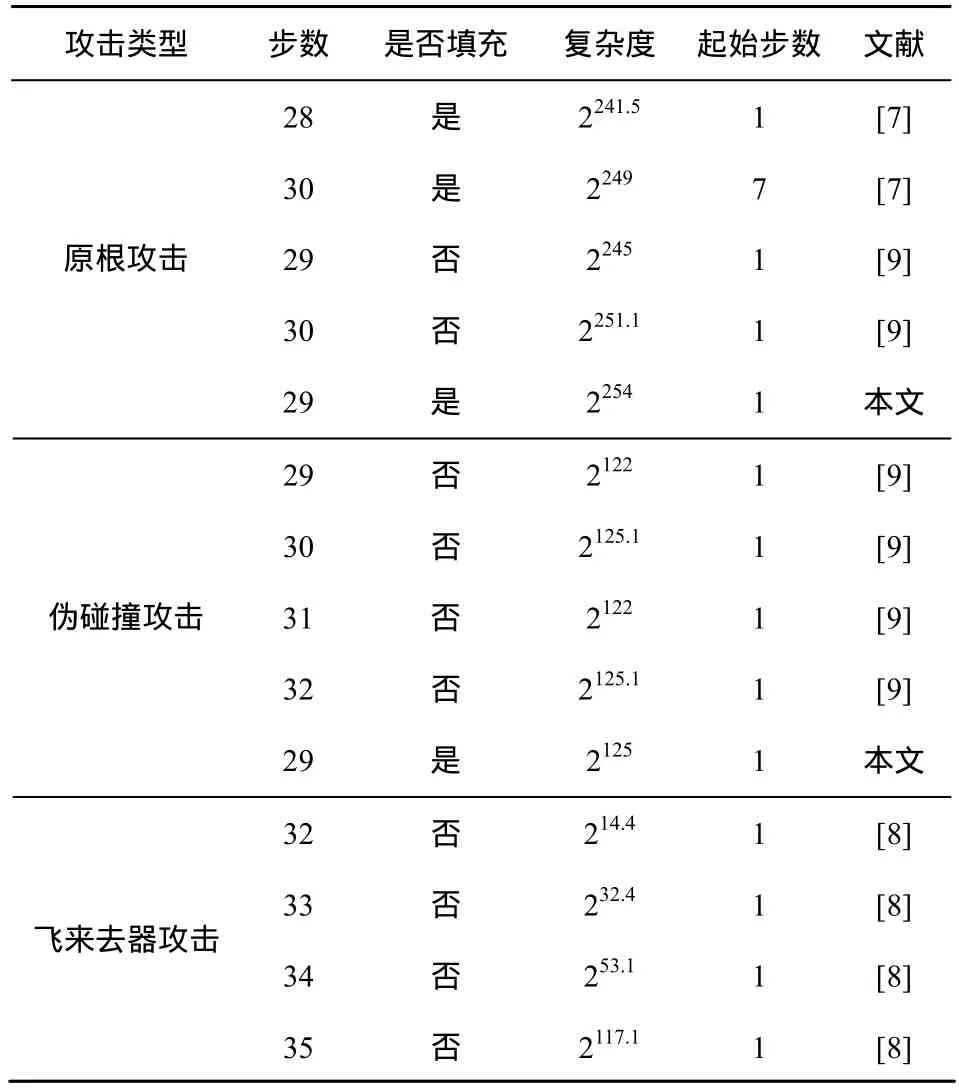
表1 SM3算法的攻击结果

5 结束语

本文给出了29步SM3算法的原根攻击，并把它转化为对29步SM3算法的伪碰撞攻击。与已知的攻击结果相比，本文的攻击是从第1步开始的，且满足消息填充。表1给出了SM3算法的攻击结果比较。虽然从第1步开始的29步SM3算法不能有效地抵抗原根攻击和伪碰撞攻击，但是由于SM3算法的快速扩散能力，完整的 SM3算法仍具有抵抗各种已知攻击的能力，具有非常高的安全性。如何发现并利用 SM3的其他特点来分析更多步数的算法是下一步的研究重点。

[1]WANG X,YU H. How to break MD5 and other hash functions[A].EUROCRYPT 2005[C]. Aarhus,Denmark,2005. 19-35.

[2]WANG X,YIN Y,YU H. Finding collisions in the full SHA-1[A].CRYPTO 2005[C]. Santa Barbara,California,USA,2005. 17-36.

[3]DIFFIE W,HELLMAN M. Exhaustive cryptanalysis of the NBS data encryption standard[J]. Computer,1977,10(6):74-84.

[4]AOKI K,SASAKI Y. Preimage attacks on one-block MD4,63-step MD5 and more[A]. SAC 2008[C]. New Brunswick,Canada,2008.103-119.

[5]National Institute of Standards and Technology. Announcing request for candidate algorithm nominations for a new cryptographic hash algorithm (SHA-3)family[EB/OL]. http://csrc.nist.gov/ groups/ST/hash/documents/ FR_ Notice_Nov07.pdf,2008.

[6]SM3 hash function[EB/OL]. http://www.oscca.gov.cn/UpFile/20101222141857786.pdf/,2010.

[7]ZOU J,WU W,WU S,et al. Preimage attacks on step-reduced SM3 hash function[A]. ICISC 2011[C]. Seoul Korea,2011.375-390.

[8]KIRCANSKI A,SHEN Y,WANG G,et al. Boomerang and sliderotational analysis of SM3 hash function[A]. SAC 2012[C]. Windsor,Canada,2012.305-321.

[9]WANG G,SHEN Y. Preimage and pseudo-collision attacks on stepreduced SM3 hash function[EB/OL]. http://eprint.iacr.org/2012/640/,2012.

[10]MENEZES A J,OORSCHOT P C,VANSTONE S. Handbook of Applied Cryptography[M]. CRC Press,1996.

[11]LI J,ISOBE T,SHIBUTANI K. Converting meetin-the-middle preimage attack into pseudo collision attack: application to SHA-2[A].FSE 2012[C]. Washington DC,USA,2012.264-286.