基于轻量云模型的WSN不确定性信任表示方法

徐晓斌，张光卫，王尚广，孙其博，杨放春

（北京邮电大学 网络与交换技术国家重点实验室，北京 100876）

1 引言

无线传感器网络（WSN,wireless sensor network）是物联网感知层的一种典型应用。WSN是一个动态的开放网络，通常部署于外界，易于出现突发故障或者遭遇敌手的恶意攻击，WSN节点的安全保护在WSN应用中尤为重要[1,2]。由于 WSN节点硬件通常较为廉价，计算能力较弱，难于实现较复杂的加密算法，仅通过传统的加密方式不足以保护WSN的安全[3]。作为对WSN传统加密安全策略的有效补充，信任管理对节点行为进行分析，使用信任值描述节点行为的可靠性，为WSN的路由选择、数据融合等提供支持，从而保证在出现攻击时，WSN能够保持可靠的运作。基于信任的WSN安全保护通常有2个主要目标：入侵的识别与入侵的容忍。入侵的识别要求信任的变化对于入侵行为有较高的敏感度，以便及时发现入侵行为；入侵的容忍要求在出现入侵行为时，尽可能不影响原有信任情况，以便顺利完成原定任务。二者存在矛盾关系。

1996年，B1aze等人首先提出了信任管理的概念[4]。之后，信任管理被应用于WSN、ad hoc等多种场景。在现有信任管理方法中，对信任的表示通常有2种方式：一种方式使用信任等级来表示节点是否可信[5]，另一种表示方式在业界应用较多，通过对节点的行为、数据等因素进行计算，使用[0,1]之间的数值表示信任。Ganeriwal等人提出的RFSN系统[6]是一个较为完整的基于信誉的无线传感器网络信任管理的框架，该方法使用直接信息和间接信息来计算信誉。然而由于对信誉的表示过于简单，该算法不具备恶嘴攻击的容忍能力。Klasniewski等人提出的 TIBFIT模型[7]参照信任值进行数据的融合，以减小误差。然而这种模型仍然无法准确描述节点信任的不确定性，灵活性较差。Momani等人提出了无线传感器网络中的贝叶斯网络信任模型(BNWSN)[8]，通过贝叶斯网络，对节点通信信任和数据信任进行整和，从而评估节点之间的信任关系，不同信任组件可以便捷的添加或删除。肖德琴等人探讨了一种基于高斯分布的传感器网络信誉模型(GRFSN)[9]，并通过仿真实验，说明了高斯分布可更好地保持信誉稳定性。杨光等人提出了一种WSN节点行为评测模型MA&TP-BRSN，将节点评价行为与通信行为区分开来，建立了对第三方节点恶意评价行为的具体测评方法[10]，该方法能在一定程度上消除高信誉节点的恶意诽谤行，然而由于最终的信任情况仅用一个数字表示，恶意诽谤识别的敏感度较低。蔡绍滨等人在信任模型和云理论的研究基础上，构建了基于云理论的无线传感器网络信任模型——云信任模型(CTM)，并将之运用到了恶意节点识别中[11]。此模型中，云模型被用做计算一次信任值的工具，信任值仍然使用一个数字表示，该方法未能很好地利用云模型解决入侵识别的敏感度与入侵容忍之间的矛盾。Bao等人提出了一个高度可扩展的集群层次信任管理无线传感器网络协议[12]，通过多种信任属性，总体评价一个传感器节点的信任，并将之应用于地理路由及其入侵检测中。现有的WSN信任管理模型大多将多种类型的行为整合为一个信任值，使用此单一数值表征节点信任情况，使用此方法可能遇到如下情况：当节点出现噪声、遭遇入侵或恶意诋毁时，若该节点信任值降低程度较高，则入侵识别敏感度较高，而入侵容忍能力相对不足，该节点将在长时间内无法按照原定计划完成任务；若信任值减低程度较低，则入侵容忍程度较高，而入侵识别敏感度相对不足，难于及时发现恶意攻击。因此，如何设计一种信任表示方法，既保证异常行为的敏感度，又实现噪声及入侵的容忍是信任评估的核心问题。

本文在已有信任管理方法研究的基础上，在不确定性定性定量转换模型——云模型[13]基础上，提出了计算简单，适用于WSN的轻量云模型。轻量云模型主要包括轻量云的表示、轻量正向云算子、轻量逆向云算子、轻量云相似度算子。使用轻量云，表征节点之间的信任关系，既描述了节点的整体信任情况，又对信任的不确定度进行了量化评估；在信任值计算时，对节点直接交互情况和邻居节点的推荐情况进行分别评估，全面表示网络中节点间的信任情况；提出了 WSN中轻量云信任(LCT，lightweight-cloud trust for sensor network)的概念，并给出了信任管理中常见的直接信任、间接信任、推荐行为信任的表示和计算方法，实现了WSN中节点信任度全面的不确定性描述。

经过仿真实验，证明了这种表示方法对于噪声和入侵既有较强的容忍能力，又有较敏感的识别能力。为WSN应用中的可信路由选择及可靠数据融合提供了基础。

2 轻量云信任

由于WSN节点硬件计算存储能力较弱，且电能受限，因此传统信息安全相关技术在WSN中不再适用，WSN应用中节点能力具备不确定性，使用云模型对WSN节点进行信任评价，能够量化评估节点信任的不确定性，既可以保证信任情况的相对稳定，又可以实现较敏感的异常行为发现。在WSN的信任管理中，如何降低算法的复杂度是一个重要问题，基于此，本文在云模型的基础上，提出了计算简单高效，且性能与云模型接近的轻量云模型，并将之运用于WSN信任表示中。

2.1 云模型

云模型是定性概念与其数值表示之间的不确定性转换模型，由我国工程院院士李德毅教授于1995年正式提出。至今云模型已成功应用到数据挖掘、智能控制、图像处理等众多领域。

定义1 云和云滴 设U是一个用数值表示的定量论域，C是U上的定性概念，若定量值x∈U是定性概念 C的一次随机实现，x对 C的确定度μ(x)∈[0,1]是有稳定倾向的随机数。

μ:U→[0,1]∀x∈Ux→μ(x)，则x在论域U上的分布称为云，记为云C(X)。每一个x称为一个云滴[13]。

正态云模型是最重要的一种云模型，可以表征自然科学、社会科学中大量的不确定现象。以云的数字特征——期望Ex、熵En和超熵He表示定量数据的定性特征，用以表示数据的整体水平、离散程度及不确定度，记做C(Ex,En,He)，称为云的特征向量。

通过正向云算法可以把定性概念的整体特征变换为定量数值表示；通过逆向云算法可以实现从定量值到定性概念的转换，将一组定量数据转换为以数字特征{Ex,En,He}表示的定性概念。

2.2 轻量云模型

在WSN中，节点计算能力有限，因而在设计WSN中算法时，应尽量以加减法为主，尽可能减少乘除法，尽量避免较复杂的计算，如开方、求对数等。WSN中计算的开销往往以乘除法的次数衡量。基于此，在云模型的基础上，提出适合 WSN中信任表示及计算的轻量云模型(LCM,lightweight cloud model)，其表示方法如下。

定义2 轻量云模型的定性 表示轻量云模型的定性表示是由2个数字特征构成的元组LC=(Ex,En)，其中，Ex(expected value)是云滴在论域空间分布的期望；En(entropy)表示熵，是定性概念随机性的度量，反映了能够代表这个定性概念的云滴的离散程度；另一方面又是定性概念亦此亦彼性的度量，反映了在论域空间可被概念接受的云滴的取值范围。

在轻量云模型中，正向云算子实现定性概念向定量数据的转换，逆向云算子实现定量数据想定性概念的转换，云相似度算子实现了2个概念之间的相似度比较。3个算子定义如下。

定义3 轻量正向云算子 轻量正向云算子ArForward(L C(E x,E n))是一个把轻量云模型的定性表示变换为定量数据集合的映射π:LC→S，满足：

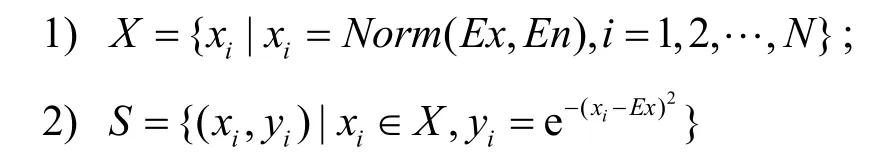
定义4 轻量逆向云算子 轻量逆向云算子ArBackward(S)是一个把定量数据集合变换为轻量云模型的定性表示的映射π:S→LC，满足：

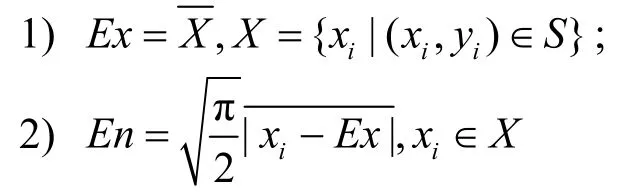
定义5 轻量云相似度算子 轻量云相似度算子 Arlikeness(L Ci(E xi,E ni),L Cj(Exj,Enj))是一个把 2个轻量云模型变换为二者相似度表示的映射π:(LCi,L Cj)→sim(i,j )，满足：

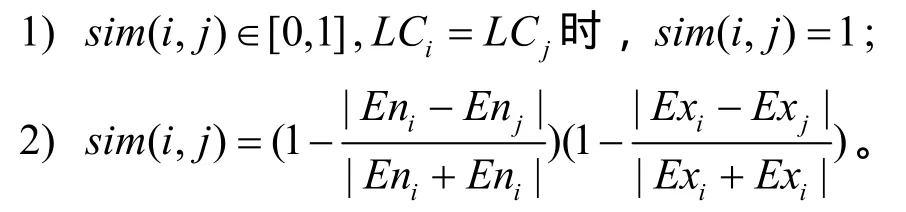
使用轻量云模型表示信任，即可以反映信任的整体水平，还能表示信任的不确定性，当信任度改变时，整体水平的变化较平缓，而不确定度的变化较剧烈。使用轻量逆向云算子，可以实现定量的信任值向定性的信任情况的映射，使用轻量云相似度算子，可以实现2个定性信任情况的相似度比较。

3 基于轻量云模型的WSN信任表示方法

信任指标是对信任值计算的基础与目标。本文综合了当前信任管理框架中的主要信任元素，提出了较为全面的信任指标，并定义了各指标的轻量云表示，在此基础上，提出了信任云算法。

3.1 信任指标及其轻量云信任

在信任管理体系中，评估信任情况的指标通常有直接信任、间接信任、推荐行为的信任等。现给出3个指标的定义如下。

定义6 直接信任 WSN中，节点根据直接交互行为得到的另一节点信任情况称为直接信任。直接信任可以通过对通信情况、数据可靠程度的分析得到。节点i对节点j的直接信任用Tij表示。

定义7 间接信任 节点通过其他节点的推荐行为得到的另一节点的信任情况称为间接信任。节点i对节点j的间接信任用STij表示。

定义8 推荐行为的信任 节点对推荐行为评估得到的信任情况称为推荐行为的信任。节点i对节点j推荐行为的信任用RTij表示。

传统的WSN信任管理模型通常将多次计算的不同信任值整合为一个信任值，这种方法往往无法兼顾入侵识别的敏感度与入侵的容忍。使用轻量云，使用二元组表示各信任指标：Tij(E x,E n)、STij(E x,E n)、 RTij(E x,E n)，以轻量云的期望作为整体信任情况，熵作为信任的不确定性。信任值改变时，期望会较为稳定，而熵对于变化较为敏感，可以兼顾入侵的容忍与入侵识别的敏感度，用户可根据应用的场景与需要，综合分析2个参数的变化，制定管理策略。这种信任表示方法称为轻量云信任(LCT,lightweight-cloud trust for sensor network)。

3.2 轻量云信任算法

直接信任、间接信任、推荐行为的信任均可通过轻量云模型中的算子进行计算，算法如下。

算法1 WSN直接信任算法

输入：节点i对节点j直接信任值{t1,t2,…,tn},n∈N*

输出：直接信任Tij

step 1：令 S={t1,t2,…,tn},n∈N*;

step 2：LC=ArBackward(S );

step 3：Tij=LC。

直接信任算法使用逆向云算子，只需2次除法1次乘法，计算较为简单，适用于WSN节点。

算法2 WSN间接信任算法

输入：节点集{k1,k2,…,kn},n∈N*向节点i推荐的节点j信任

输出：间接信任STij

step 2：Ex={e xi|(e xi,e ni)∈S},i=1,2,…,n ；

step 3：En={e ni|(e xi,e ni)∈S},i=1,2,…,n ；

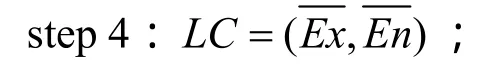
step 5：STij=LC。

间接信任算法只需2次除法，计算较为简单，适用于WSN节点。

算法3 WSN推荐行为信任算法

输出：推荐行为的信任RTij

step 2：S={simt},t=1,2,…,n ；

step 3：LC=ArBackward(S)；

step 4：RTij=LC。

推荐行为信任算法使用云相似度算子及逆向云算子，只需4次除法2次乘法，计算较为简单，适用于WSN节点。

使用LCT，直接信任、间接信任、推荐行为的信任计算与更新条件与具体安全策略有关。一般情况下，直接信任的计算与更新在与目标节点交互后开始；当节点第一次与目标节点交互，未存储其直接信任时，需要进行信任的推荐，计算间接信任；推荐成功后，与目标节点进行交互，并进行推荐行为信任的评估。

4 仿真实验

基于LCT的信任表示方法，既可以实现对入侵识别的敏感度，还可以实现对多种入侵的容忍。通过对WSN中场景进行模拟，对多种入侵情况下节点的 3个信任指标进行计算，并与文献[11]中提出的CTM进行了对比分析，验证LCT的有效性。

4.1 实验设计

实验使用的无线节点由SoC zigbee芯片CC2530、加速度传感器、PCB天线、电源电路以及JTAG调试接口组成。对实验场景进行定制设计：WSN中共有150个节点，协议使用802.15.4，节点间平均距离10 m，节点工作的占空比为5%。选取实验场景中一个节点i与室内新节点j以及室外旧节点k通信情况进行分析，每小时统计一次数据发送成功率。对20次数据发送成功率使用正态分布进行统计，如表1所示。

表1 节点通信成功率

基于以上实验结果中的数据，设计仿真实验，对信任指标进行分析。仿真环境建立的PC机配置为：Intel(R)i5-2450M CPU @ 2.50 GHz，RAM=2 GB，Windows 7操作系统。所采用的仿真环境为Matlab2011Rb。以2个节点间直接信任数据为基础，模拟推荐数据及攻击数据，在以上环境中进行多种场景下信任指标的仿真，并对结果进行分析。

4.2 多攻击场景入侵容忍及识别

4.2.1 On-Off攻击容忍及识别

On-Off攻击首先通过正常的行为积累信任度，之后进行恶意攻击。这种攻击方式利用了信任的评价，是较典型的针对信誉系统的攻击[11]。假设攻击节点 j与i进行交互，前50个小时进行正常数据发送，积累信任，之后按照正态分布 N(0.5,0.16)进行选择性转发，此时信任大大降低。在这组仿真实验中，直接信任在最近20次信任值的基础上进行计算，间接信任在5个邻居节点直接信任的基础上进行计算，仿真得到直接信任、间接信任曲线，如图1所示。

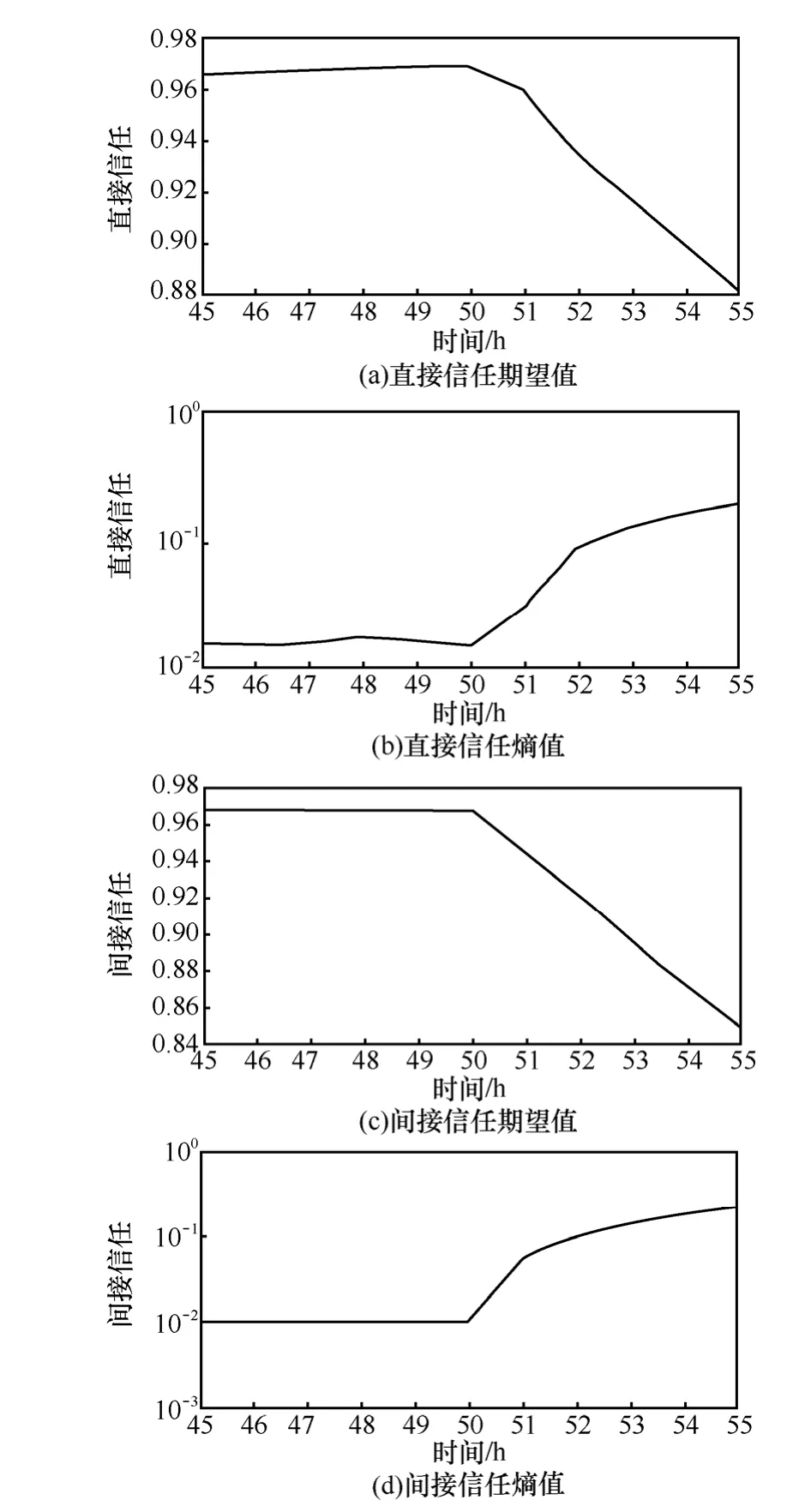
图1 j遭遇On-Off攻击，Tij及STij变化曲线

从图 1中可以看出，使用 LCT，WSN遭遇On-Off攻击时，信任的期望降低，说明信任整体水平下降；信任的熵增高，说明信任的不确定度变大。间接信任相比直接信任变化更为明显。

为了进一步验证 LCT在入侵容忍与入侵识别敏感度方面的作用，在相同的场景下，使用 CTM进行信任评估。采取文献[11]中的参数设置，节点i、j共同邻居数为5个，直接信任与间接信任的权值w1，w2分别为定义为0.8和0.2，衰减因子w为0.3，上升幅度m为1，下降幅度n为2，仿真得到信任变化曲线如图2所示。

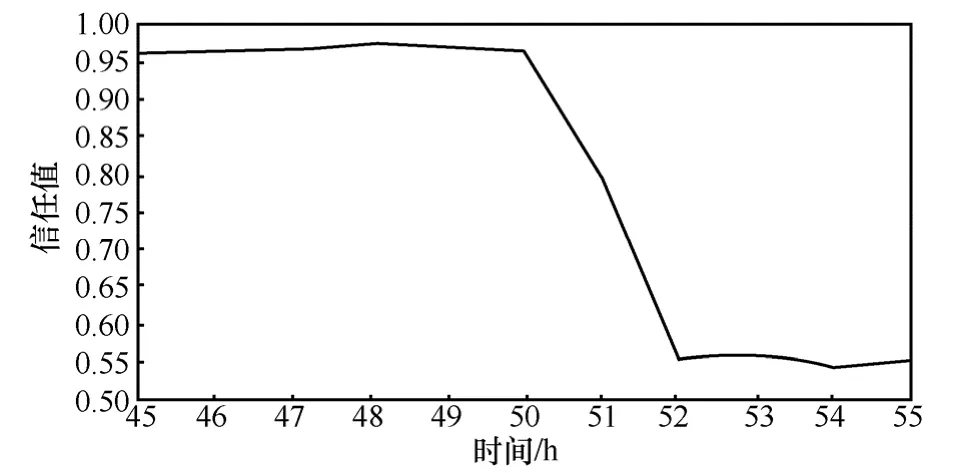
图2 j遭遇On-Off攻击，CTM信任值变化曲线

从直观上看，使用LCT，当On-Off攻击出现时，轻量云信任直接信任、间接信任的期望降低均较平缓，能够保证入侵的容忍；而熵数值的增加较剧烈，能够保证入侵行为的敏感识别；而使用CTM计算信任值，入侵识别敏感度与入侵容忍能力的平衡由下降幅度n决定[11]，无法兼顾二者。使用变化幅度dv量化评估信任指标变化的剧烈程度，dv计算公式为dv=(Vnew-Vold)/Vold，当dv大于0时，指标上升，小于0时，指标下降，dv绝对值越大，信任指标变化越剧烈，对入侵的敏感度越高，绝对值越低，信任指标变化越平缓，入侵容忍能力较高。在第51个小时，攻击刚刚出现时，LCT与CTM信任指标的变化幅度对比如表2所示。

表2 On-Off攻击出现时，LCT与CTM信任指标变化幅度对比

根据表2，当On-Off攻击出现时，LCT直接信任、间接信任期望降低程度分别为CTM降低程度的1/20、1/7左右，对入侵的容忍能力较高；而LCT直接信任、间接信任熵的增加程度分别为CTM降低程度的6倍、26倍左右，识别入侵的敏感度较高。在LCT中，直接信任相比间接信任入侵容忍能力较高，而入侵识别的敏感度较低。在第 51小时，发现节点j信任的变化时，若在应用中需要对信任的变化具备一定容忍能力，则可基于信任指标的期望制定应对策略，若需要及时发现入侵，则可基于信任指标的熵制定应对策略。

根据上述实验对比及分析，可知使用LCT，在WSN中出现入侵时，用户易于根据应用的需要，综合应用LCT的信任参数，制定更多的应对策略。

4.2.2 恶嘴攻击容忍及识别

如果WSN节点被敌手捕获，内部程序被修改，修改后的节点并不进行直接的恶意攻击，而是在推荐过程中，篡改信任数据，对目标节点进行恶嘴攻击，诋毁其信任。在此情况下，进行信任管理框架下的仿真实验。

假设节点在运行50个小时后，遭遇恶嘴攻击，在节点i要求对节点j进行推荐时，5个邻居中k对j发起恶嘴攻击，按照正态分布N(0.5,0.16)伪造节点j信任值，并将伪造的信任值发送给i。仿真得到间接信任、推荐行为的信任的曲线，如图3所示。

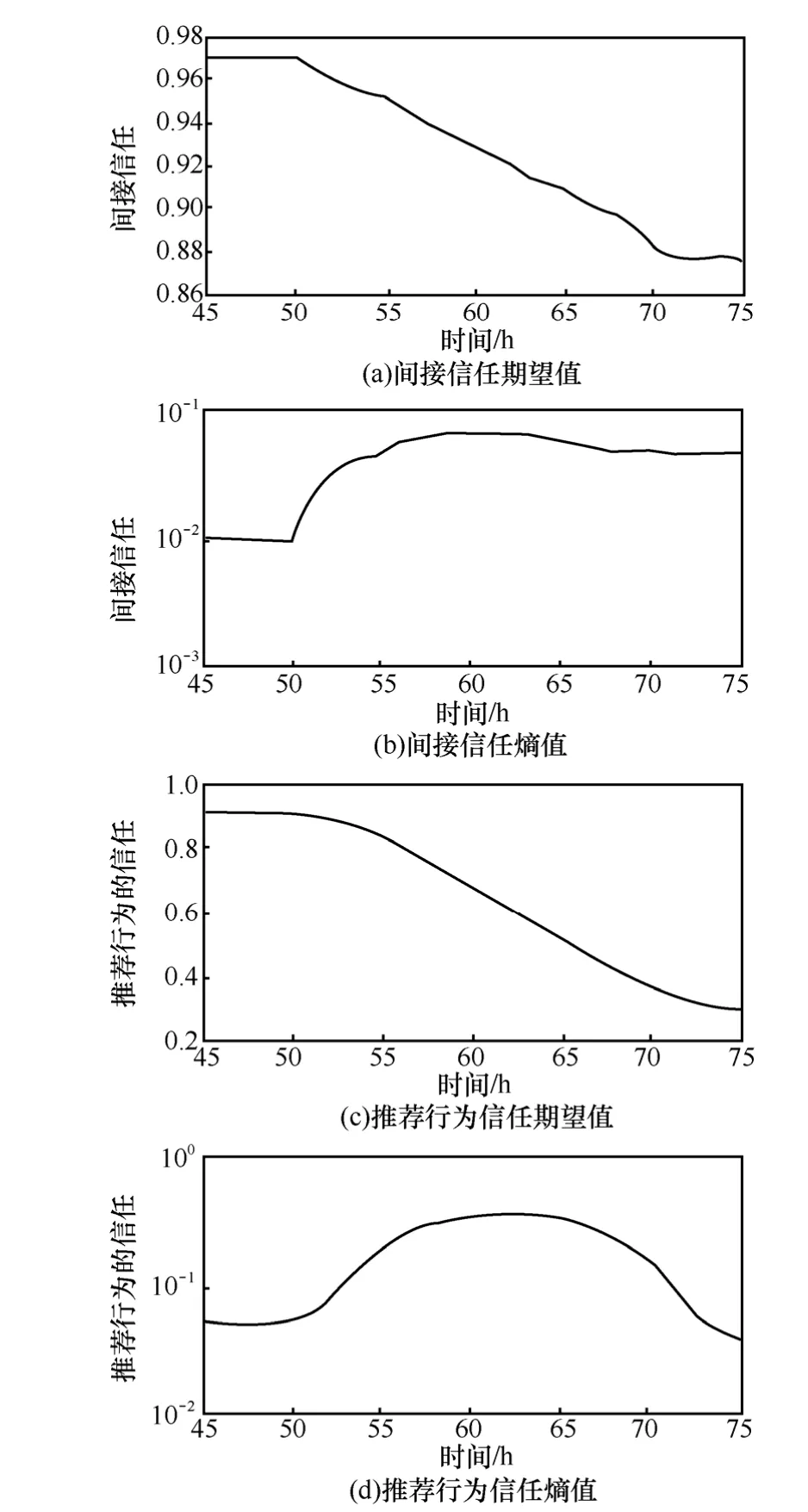
图3 j遭遇k恶嘴攻击，STij及RTij变化曲线

从图3中可以看出，当出现恶嘴攻击时，间接信任的期望降低，然而减低速度较平缓，最终信任值仍与实际信任值较接近，具备对恶嘴攻击的容忍能力；而此时间接信任的熵骤增，用户易于判断，WSN中可能存在攻击行为；同时，节点k推荐行为的信任期望骤降，熵骤增，且期望最终降低为0.4以下，用户可判断出节点j遭遇节点k恶嘴攻击。节点信任指标的变化既保证了对恶嘴入侵的容忍，又敏感地识别了攻击行为。在相同场景下使用 LCT进行仿真实验，参数设置与上组实验相同。仿真结果如图4所示。

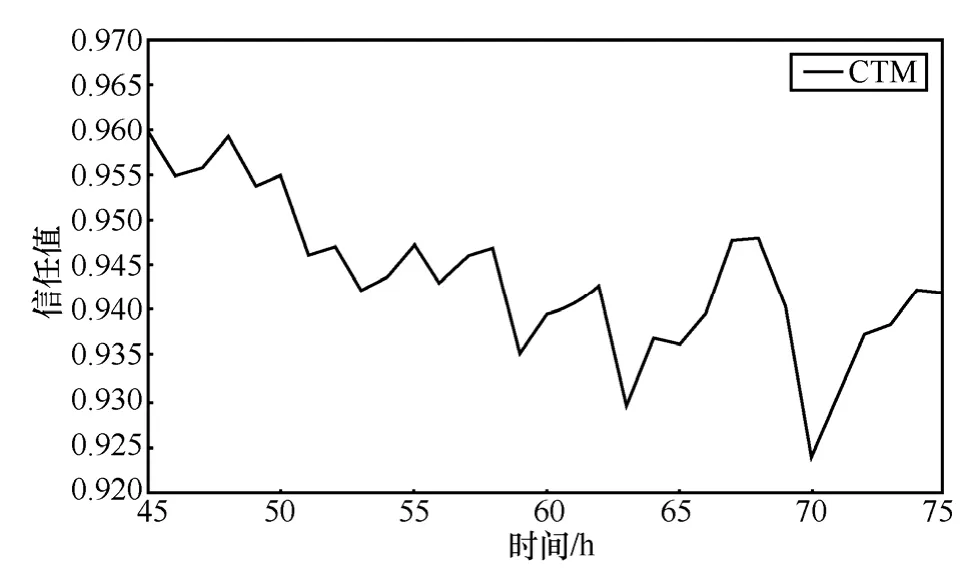
图4 j遭遇k恶嘴攻击，CTM信任值变化曲线

根据图4可以看出，当出现恶嘴攻击时，CTM信任值变化较小，最终信任值仍然高于0.92，对于恶嘴攻击的容忍度较高，然而由于信任值变化的不明显，用户无法发现恶意节点 k，在这种场景下，CTM对入侵的容忍能力较高，然而入侵识别的敏感度较弱，无法兼顾二者。

4.3 开销分析

由于WSN中，节点电能有限，在制定安全策略与算法时，还需要考虑算法的开销，并分析对节点寿命的影响。由于WSN中加减法时间复杂度远小于乘除法、开平方复杂度，因此计算开销仅仅比较乘除法及开平方次数。当一个节点平均具有5 个邻居节点，簇的平均大小为20，并且每个节点根据最近10次信任计算信任云时,统计LCT与CTM更新平均所需的乘除法以及次数，如表3所示。

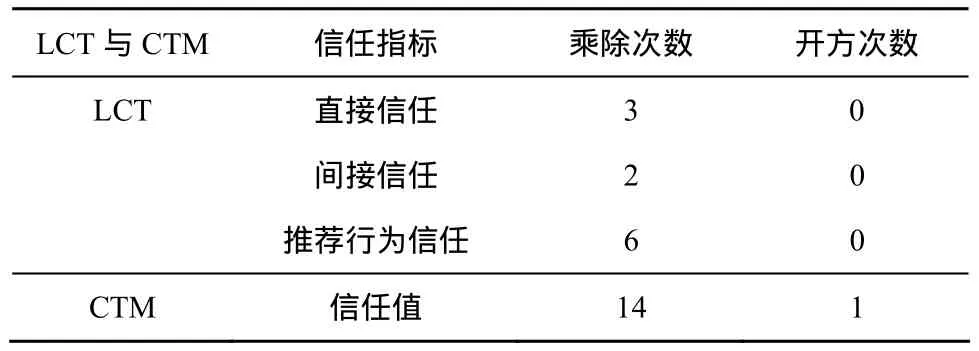
表3 LCT与CTM计算开销对比

在仿真实验的应用场景中，每个节点第一次交互需要计算间接信任，之后需要建立直接信任云，并计算推荐行为的信任，第一次交互需要11次乘除法计算，之后每次交互只需更新直接信任即可，每次只需3次乘除法计算，远小于CTM的开销。当用户制定复杂的信任管理策略，发起更多信任计算要求时，计算开销会增大，然而由于WSN节点执行每条指令所消耗的电量为发送1 bit数据所消耗电量的1/1000[14]，一般情况下，使用LCT对节点寿命的影响可以忽略不计。

5 结束语

本文根据对WSN应用特点及场景的分析，提出了信任管理中入侵容忍能力与入侵识别的敏感度是2个重要且存在矛盾的目标，为了克服2个目标之间的矛盾，实现既具备容忍能力，又具有入侵识别敏感度的信任管理，设计了基于轻量云模型的信任表示方法。并根据典型的WSN应用场景，对此信任表示方法进行了仿真实验，实验结果证明，在WSN中出现On-Off攻击、恶嘴攻击时，使用该方法，既能保证入侵的容忍，又能实现入侵行为的敏感识别。LCT算法简单，对WSN寿命的影响可以忽略，具有较高的可用性。

下一步的研究工作为：搭建大规模的物理实验网络，在其基础上，使用基于轻量云模型的信任表示方法构建WSN的安全与信任网络，并研究基于信任的增强路由协议、数据融合算法等。

[1]PERRIG A,SZEWCZYK R,WEN V,et al. SPINS: security protocols for sensor networks[J]. Wireless Networks,2002,8(5): 521-534.

[2]WATRO R,KONG D,CUTI S F,et al. TinyPK: securing sensor networks with public key technology[A]. Proceedings of the 2nd ACM Workshop on Security of Ad hoc and Sensor Networks[C]. New York,USA,2004.59-64.

[3]荆琦,唐礼勇,陈钟. 无线传感器网络中的信任管理[J]. 软件学报,2008,19(7):1716-1730.JING Q,TANG L Y,CHEN Z. Trust management in wireless sensor networks[J]. Journal of Software,2008,19(7):1716-1730.

[4]BLAZE M,FEIGENBAUM J,LACY J. Decentralized trust management[A]. IEEE Conference on Security and Privacy[C]. Oakland,California,USA,1996.164-173.

[5]GANERIWAL S,BALZANO L K,SRIVASTAVA M B. Reputation-based framework for high integrity sensor networks[J]. ACM Transactions on Sensor Networks,2008,4(3): 15.

[6]黄海生,王汝传. 基于隶属云理论的主观信任评估模型研究[J]. 通信学报,2008,29(4):13-19.HUANG H S,WANG R C. Subjective trust evaluation model based on membership cloud theory[J]. Journal on Communications,2008,29(4):13-19.

[7]KRANSNIEWSKI M D,VARADHARAJAN P,RABELER B,et al.TIBFIT:trust index based fault tolerance for data faults in sensor network[A]. International Conference on Dependable Systems and Networks[C]. Washington DC,USA,2005.672-681.

[8]MOMANI M,CHALLA S,ALHMOUZ R. BNWSN: Bayesian network trust model for wireless sensor networks[A]. Mosharaka International Conference on Communications,Computers and Applications[C]. Amman,Jordan,2008.110-115.

[9]肖德琴,冯健昭,周权等. 基于高斯分布的传感器网络的信誉模型[J]. 通信学报,2008,29(3):47-53.XIAO D Q,FENG J Z,ZHOU Q,et al. Gauss reputation framework for sensor networks[J]. Journal on Communications,2008,29(3): 47-53.

[10]杨光,印桂生,杨武等. 无线传感器网络基于节点行为的信誉评测模型[J]. 通信学报,2009,30(12): 18-26.YANG G,YIN G S,YANG W,et al. Reputation model based on behaviors of sensor nodes in WSN[J]. Journal on Communications,2009,30(12): 18-26.

[11]蔡绍滨,韩启龙,高振国等. 基于云模型的无线传感器网络恶意节点识别技术的研究[J]. 电子学报,2012,40(11):2232-2238.CAI S B,HAN Q L,GAO Z G ,et al. Research on cloud trust model for malicious node detection in wireless sensor network[J]. Acta Electronica Sinica,2011,40(11):2232-2238.

[12]BAO F,CHEN R,CHANG M J,et al. Hierarchical trust management for wireless sensor networks and its applications to trust-based routing and intrusion detection[J]. IEEE Transactions on Network and Service Management,2012,9(2): 169-183.

[13]李德毅,杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社,2005.LID Y,DU Y. Artificial Intelligence with Uncertainty[M]. Beijing:National Defence Industry Press,2005.

[14]CHENG S,LI J,REN Q,et al. Bernoulli sampling based (ε,δ)-approximate aggregation in large-scale sensor networks[A]. Proc of the 29th IEEE INFOCOM[C]. San Diego,CA,USA,2010.1181-1189.