预学·导学·善学

洪菲菲+陈志良

摘 要：“预学·导学·善学”模式在小学数学教学中的运用有良好的效果。预学是在新授课之前，学生在教师指导下开展的预习；导学是在学生预习基础上进行针对性的引导，并给予学生充分的学习时空；善学是引导学生提炼数学方法、领悟数学思想，掌握数学技能，使之成为学生的学习能力。

关键词：小学数学；“三学”模式；预学；导学；善学

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2014）17-0067-03

自上世纪90年代，洋思中学、杜郎口中学开展“先学后教”教学改革实验大获成功之后，“先学后教”模式在全国各地刮起一阵效仿风潮。不可否认，“先学后教”模式符合“实践——认识——再实践——再认识”的认识论基本规律，尊重了学生个体的差异性和独特性，彰显了学生的主体角色。然而，在实际操作中，该模式也不可避免地存在着一些弊端。例如，教学目标实现上，片面追求“立体式、大容量、快节奏”的技能训练，可能导致智能的“窄化”和情意的“剥落”；教学过程中，“学”与“教”被机械地分割，可能导致“先学”与“后教”的断裂与错位等等。我校自2011年开始进行“三学”课堂教学模式的实践与探索，试图在激发学生学习自主性、提升课堂效率上做文章，取得了一定成效。

一、预学——简而精

在预学上，我们采用了“三个一”的操作方式，即“每日一提醒、每日一问题、每日一练习”。“每日一提醒”是教师对学生自学新课内容时提出的建议，或提示预习的方法，或提醒新课内容与旧知识之间的联系，或点明新课中的几个知识点。一言以蔽之，就是先让学生对新课内容有个大致的了解，对如何预习有个方向。“每日一问题”是预习的“主心骨”，教师要针对新课内容，提出一个最核心、最有价值的问题，使学生在问题的导引下，对新课内容进行学习和思考，想明白了该问题对新课知识也就有了一定的理解和掌握。这是学生预学的“拐杖”，也是预学过程中的一盏“航标灯”。“每日一练习”是针对新课内容设计的一至两道练习，意在让学生通过练习自行检测预习效果，同时也是教师了解学生预习情况的一个凭借。练习的题量要精简，设计要精心，指向要精准。要从简单的练习中反映出学生预学中已掌握的内容并暴露出存在的问题。例如，在“分数四则混合运算”一课中，布置了这样的预习作业：

每日一提醒：在学习新课之前，先复习一下整数四则混合运算的运算顺序。

每日一问题：通过自学课本，你能说说分数四则混合运算的运算顺序是怎样的吗？

每日一练习：请试着完成下面两道题目

在“每日一提醒”中，教师对学生提出了复习旧知的要求，暗示了新知与旧知之间的联系，帮助学生“以旧引新”。“每日一问题”中，设计了本节课内容的核心问题，给予学生明确的预习指引，防止学生模糊预习焦点。在“每日一练习”中，第一道题目考查学生对于分数四则混合运算的掌握情况；第二道题目考查学生是否会因为数据特点的影响而动摇了运算顺序的认知。简单的“三个一”，高度浓缩了预习的要求，达到了简洁、有效的预学效果。

二、导学——准而巧

学生通过预学，对新知有所了解掌握。教师要尽可能了解学生的预学情况，在学生认知的新起点上展开教学。了解学生的预学情况可以通过三个途径，一是课前快速浏览学生的预习作业；二是上课伊始，先让学生汇报预习情况，充分表达他们在预学中的所得和所思；三是教师通过解读教材和学生，预测学生预学后可能存在的问题。“三学”课堂的初衷是调动学生学习的自主性，因此，课堂实施的关键不在于“教”，而在于“导”。教师要善于做学生的“大同学”和“引路人”，继续给予学生充分的学习时空。

（一）导在“未明”处

学生预学之后，对于一些简单的、操作性强的学习技能掌握较好，但对于内隐的知识难点、数学思想方法等难以参透。学生不懂的地方，正是教师“导”的地方。这需要教师对学生的学情“把脉”，有的放矢地进行引导。例如，人教版五年级下册“最大公因数”一课，因之前有因数、倍数等知识作铺垫，预学后学生对于什么是公因数和最大公因数，怎么找最大公因数都有了比较好的掌握。在学生汇报预学情况之后，教师出示题目：“有一张长方形纸，长70厘米，宽50厘米。如果要剪成若干个同样大小的正方形而没有剩余，剪出的最大的小正方形边长是几厘米？”引导学生理解题意并尝试作答。教师注重启发学生思考：这道题求的是什么？怎么理解求最大的小正方形的边长就是求70厘米和50厘米的最大公因数？学生结合画草图、小组讨论等途径，理解了最大公因数在实际生活中的运用，建立最大公因数的生活原型。在这里，教师没有在学生掌握较好的“找最大公因数”上大做文章，而是准确抓住了学生预学之后认知模糊的地方，即不能理解找到最大公因数在生活中的实际应用这个“未明”处展开教学。“打蛇打七寸”，找到了学生预学中存在的困惑并着重引导，才能实现有效教学。

（二）导在“关键”处

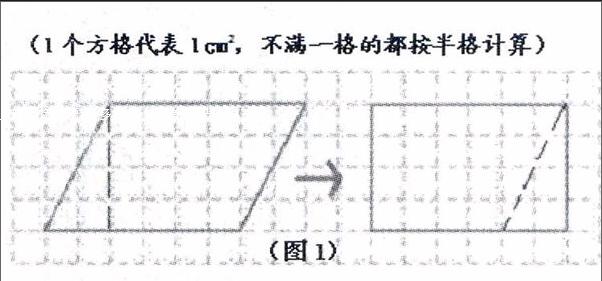
在预学汇报中，学生往往能“依葫芦画瓢”，说出不少门道来。这时，教师切不可被表面的“繁荣”所迷惑。学生的理解往往浮于表面，教师要紧紧抓住新知中的“关键”点，引导学生在理解上进行深挖，以达到突出重点、突破难点的目的。例如，在“平行四边形的面积”一课中，学生通过预学大都能通过割补法将平行四边形剪拼成长方形，并找到平行四边形的底和高与转化之后的长方形的长和宽之间的关系，从而推导出求平行四边形面积的方法。表面上看，学生似乎已经掌握了所有知识点，其实学生此时的操作、认识都仅停留在表面模仿的阶段。在教学过程中，教师仍要抓住“数方格”的方法进一步展开教学（如图1）。从“割补法”回到“数方格”，看似教学思维走向发生了回转，其实这是引导学生由表入里的关键一步。通过“数方格”，不仅可以找到将平行四边形转化为长方形的直观依据（通过剪拼，将不满1格的部分拼成整格），而且有助于学生重温“面积”的含义（即图形中包含几个面积单位）。平行四边形的面积不再是虚无缥缈的概念，而能实实在在地呈现在学生面前。在直观感受面积意义的情况下，重新理解平行四边形与转化之后的长方形之间的关系，使学生对于平行四边形面积公式推导有了直观的支撑和深入的认识。

（三）导在“衔接”处

数学知识不是以“点状”的形式存在，而是有着横向或纵向的联系，并形成有严密逻辑的知识网络。学生在预学中，多以“点”的视角看待新知，体察不到新知与旧知之间的联系，教师在课堂上要有意识地点拨引导。例如，在学习“最小公倍数”之后，教师启发学生思考：求两个数的最小公倍数和最大公因数有哪些联系和区别？通过讨论，学生们发现了两个数的公因数是有限的，而公倍数是无限的。当两个数成倍数关系时，较小数是它们的最大公因数，较大数是它们的最小公倍数；当两个数成互质数关系时，它们的最大公因数是1，最小公倍数是两个数的乘积。教师引导学生在知识的衔接点进行了无缝链接，使原本零散的知识碎片有机整合，有利于学生对新知的重组和掌握。

三、善学——凝而深

“三学”课堂是否高效，很大程度上取决于学生的预学情况。而预学效果与学生的自学能力息息相关。引导学生总结学习经验，提升学习能力，是三学课堂的另一价值追求。在课的最后，教师要带领学生梳理知识，回顾预学和课堂学习过程，从中发现隐匿在知识背后的数学思想，提炼好的学习方法，以推进学习能力的不断发展。例如，在学习“3的倍数特征”之后，教师带领学生重温整个学习过程，提炼出“发现问题——提出猜想——验证猜想——得出结论——应用结论”的学习方法，并联系“商的变化规律”等旧有知识，使学生感受到这种探究思路在数学学习中的广泛应用。又如，学习分数乘除法应用题之后，学生对于用线段图帮助厘清解题思路有了更深的体会。如果将画线段图仅作为解决问题的一个工具，也就大大削弱了其价值。教师应当引导学生感受“数形结合”的优势，进一步发展“数形结合”思想，这对学生的后续学习将产生更加深远的影响。在学习知识的同时，注重学习方法的提炼，数学思想的渗透，这是“三学”课堂给教师的教学行为带来的新变化。

纵观“三学”课堂模式，其主旨是将学习活动前置，调动学生的学习主动性，使学生能以主人翁的姿态积极参与课堂学习。由于有了“预学”的铺垫，课堂效率大大提升，实现了教师的“精讲”和学生的“多练”，使当堂的巩固反馈得以实现。课后，学生不必再为繁复的练习作业所牵绊，能腾出更多的时间投入对新知的预学中。这是一个良性循环，促使着师生以更加积极的心态参与教学活动，在一定程度上实现了“减负提质”。

参考文献：

[1]屠锦红，李如密.“先学后教”教学模式：学理分析、价值透视及实践反思[J].课程·教材·教法，2013，3：24～29.

[2]韩立福.“先教后学”、“先学后教”和“先学后导”的教学思维探析[J].教育理论与实践，2012，35：48～50.