对一道沿绳加速度问题的深入研究

陆天明

（南京师范大学附属中学江宁分校，江苏 南京 211102）

紧绷轻绳上的各点沿绳方向上的速度是相等的，这是一个在中学阶段非常有用的结论.我们能否据此认为沿紧绷绳的加速度也一定相等呢？让我们先来看高中物理竞赛教材或参考书都会选用的一个问题.

如图1所示，长为L的杆AO用铰链固定在O点，以角速度ω围绕O点转动，在O点的正上方有一个很小的定滑轮B.一根轻绳绕过滑轮B，一端固定在杆的A端，另一端悬挂一质量为m的重物C，O、B之间的距离为h，求：当AB绳与竖直方向成θ角时，绳上的张力.

图1

图2

文献一般都会提供如下解法.

如图2所示，A点的速度为

设∠AOB＝α，在△OAB中，

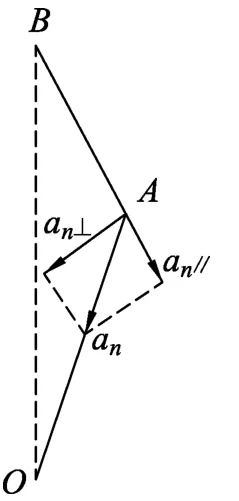
图3

把（1）、（3）式代入（4）式可得

因为OA杆做匀角速度转动，所以A点相对O点只有向心的加速度为an＝ω2L.如图3所示，将此加速度分解成沿BA方向的加速度an∥和垂直于BA方向的加速度an⊥两个分量.

考虑到（2）式，可得

这也是C上升的加速度aC，再由T-mg＝maC，可得绳上的张力

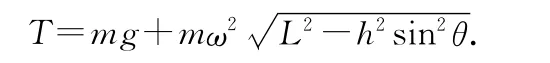
以上求解看起来非常严密，但实际上是错误的．错误的根源在于解题者想当然地认为绳上各点沿紧绷绳的加速度一定是相等的．虽然紧绷轻绳上的各点沿绳方向上的速度是相等的，但我们不能据此认为沿紧绷绳的加速度也一定相等．

B C段沿直线运动，绳上加速度处处相等，而A B的运动情况与B C段的运动方式不同．A B绳子上各点沿绳方向的加速度即径向加速度，来源于两个方面：一个是由于速度方向变化而产生的指向B点的向心加速度a1，在A B绳上的不同点这个加速度的大小是不同的；另一个是由于沿绳方向上速度大小发生变化而产生的加速度a2，在绳子的不同地方，这个加速度的大小是相等的．所以，总的看来A B绳上不同点的径向加速度是不同的．不难看出，a2才是物体C向上运动的加速度．如何求出a2呢？

设任一时刻绳子A B的长度为Lx，在△A O B中，

可以解出

A点由于速度方向变化而产生的指向B点的向心加速度大小a1为

这才是正确的结论．

其实，本题可以直接利用高等数学．将（5）式对时间求导，可得

将（7）式对时间求导可得

化简得

与（5）式比较可得

把（13）式代入（12）式同样可以得到（10）式.

最后让我们用理论力学中相关知识加以验证.

A点的沿绳子方向上的加速度即径向加速度的极坐标表达式为

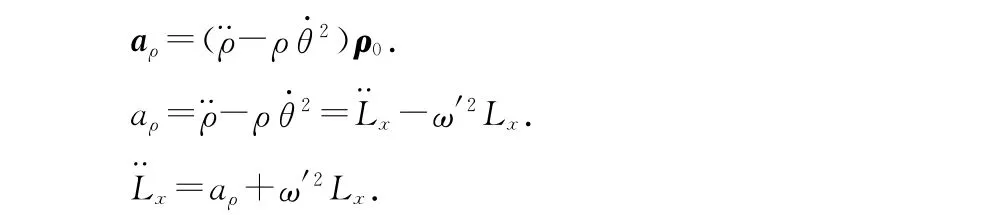
aρ就是（6）式中的an∥，所以

物体C的加速度是由于绳子的长度的变长而产生的，

将（6）、（7）、（13）式代入，便得到（10）式.

实际上，θ对应的绳与杆所成的角既可以是钝角，也可以是锐角.以上只讨论了绳与杆成钝角的情形，对于成锐角的情形，讨论方法同上，不再赘述.

总之，虽然绳上各点沿绳的速度相等，但我们绝不能据此认为这些点沿绳子方向的加速度也相等，因为绳子的转动也会产生一个沿着绳子方向的加速度，而且不同点的这个加速度又不同，所以，绳子上的各点沿着绳子方向上的加速度一般是不等的.

1 庞泽俊.评析一道物理竞赛题的解法［J］.物理教师，2008，29（8）：63-65.

2 陆天明.荣誉物理（力学部分）［M］.南京：东南大学出版社，2013：128-129.