点击几何光学难题的求解策略
杨丽芬 孙国标
(1.绍兴市鲁迅中学,浙江 绍兴 312030;2.绍兴市柯桥中学,浙江 绍兴 312030)
几何光学试题通常以折射率为核心,考查光的反射、折射、全反射、色散等知识.在高三复习中,笔者发现有些光学试题综合度大,数学要求高、灵活性强,学生求解较为困难.下面笔者归纳了求解几何光学难题的4种策略,但求予读者以点滴启发.
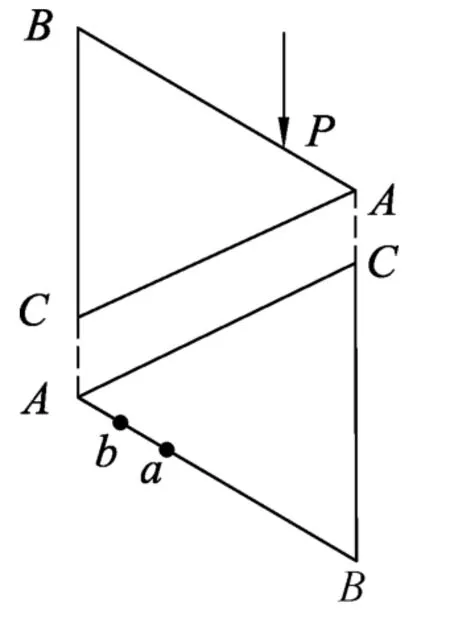
图1
1 勤作光路,寻求角度关系
例1.如图1所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后,变为从a、b两点射出的单色光,对于这两束单色光
(A)红光在玻璃中传播速度比蓝光大.
(B)从a点射出的为红光,从b点射出的为蓝光.
(C)从a、b两点射出的单色光不平行.
(D)从a、b两点射出的单色光仍平行,且平行于BC.
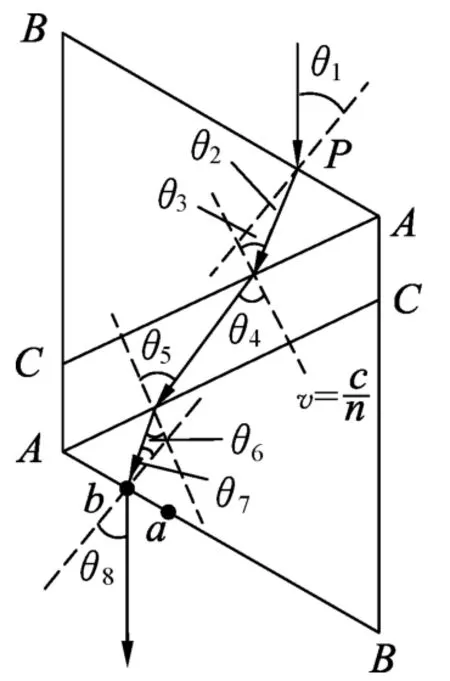
图2
解析:由于红光在玻璃中的折射率小于蓝光的折射率,在玻璃中传播速度为v=,因此(A)选项不难判断是正确的.本题的难点在于:红光与蓝光出射时是否平行?直接观察不易得到结果,但若能作出光路图,找到角度关系,问题便迎刃而解.
作出某一颜色光的光路如图2所示,由几何关系得,θ2+θ3=∠A,θ6+θ7=∠A,又因为sinθ1=nsinθ2,nsinθ3=sinθ4,θ4=θ5,sinθ5=nsinθ6,nsinθ7=sinθ8,从而得到θ3=θ6,θ2=θ7,θ1=θ8,即出射光与入射光平行.又因为蓝光折射率大,因此出射时红光应在蓝光的右侧且平行射出,故正确选项为(A)、(B)、(D).
思路点拨:画光路图是求解几何光学的问题的基本策略,而且应“边作图边找几何关系”.
2 巧用对称,转换光路
例2.截面为等腰直角三角形的棱镜称为全反射棱镜,如图3所示,由a、b两束单色光组成的复色 光沿PO方向斜射向一全反射棱镜ABC的BC面,经AB、AC面反射后从BC面射出.已知a光的频率小于b光的频率,棱镜对a、b单色光的折射率均大于.则下列说法正确的是
(A)经BC面射出的a、b光一定都与OP方向平行.
(B)经BC面射出的a光位置比b光更靠近O点.
(C)a、b光在AB、AC面上一定都会发生全反射.
(D)a、b两束光从BC射入到BC射出的路程相同.
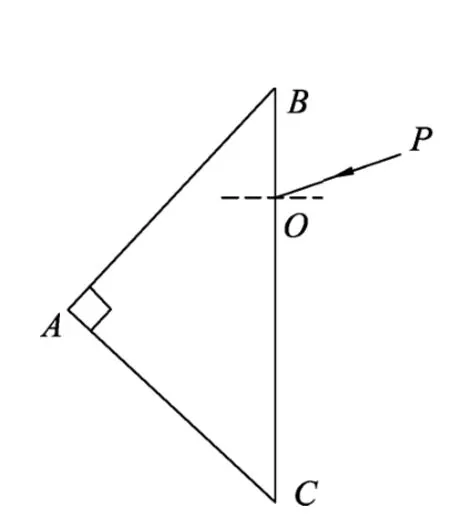
图3
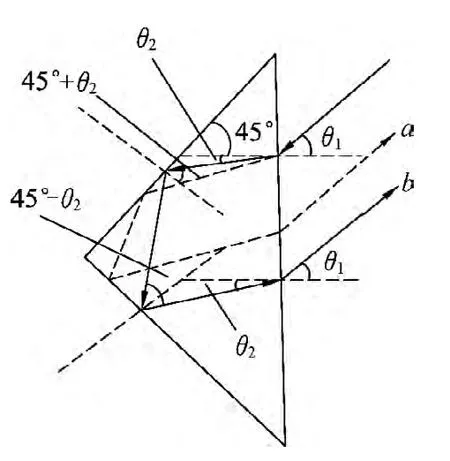
图4
解析:与上例的方法相同,根据几何关系,作光路如图4所示,第1次折射的折射光线应与第2次折射的入射光线平行,则得到出射光线应与入射光线平行,且a光的折射率小于b光的折射率,因此a光第一次折射的折射角应大于b光,作出光路如图4中虚线所示,故a更靠近O点,故(A)(B)正确.而各色光在全反射棱镜的的临界角均小于45°,故AB面反射时的入射角为45°+θ2,可以发生全反射,而AC面反射时的入射角为45°-θ2,不一定可以发生全反射,故(C)选项错误.
但本题的难点在于(D)选项,a、b两束光从BC射入到BC射出的路程是否相同?有学生从光路图中粗略地可以看出两路程不相同,但没有根据.其实,如果我们利用对称性,转换光路,问题便迎刃而解.
如图5所示,作△AB′C,使其与△ABC关于AC 对称,作△BB′C′,使其与△BB′C 关于BB′对称.对b光而言,将DE光线延长交B′C于G,由几何关系不难证明EF和EG关于AC对称,因此可以将光线DEF等效为DEG,同理将OD延长,交B′C′于H点,由几何关系得DH与DG关于BB′对称,因此可以将光线ODEG等效为ODH,同理a光走过的路程可以等效为OH′,所以a光走过的路程长,(D)选项错误.
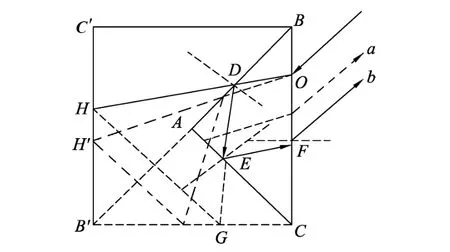
图5
思路点拨:在研究光的反射时,利用对称性,将反射光线作镜面对称,可以将光线等效成直线传播,在研究镜面间多次反射问题时极为方便.
3 分析特殊光线,明确光路走向
例3.如图6所示,半径为R的1/4透明圆柱体固定于地面上,透明体对红光的折射率为n.今让一束平行于地面的红光射向圆柱体的左侧,经折射后红光照射到圆柱体右侧的地面上.下列说法中正确的是
(A)红光能从圆柱体的右侧的圆弧面上的任一点射出,因为折射,出射后的光线不是平行光.
(B)从圆柱体的圆弧面上射出的光线能将圆柱体右侧的地面照亮,且照亮的区域比阴影长度长.
(C)折射率n越小,圆柱体右侧地面上的阴影长度越长.
(D)折射率n越大,圆柱体右侧地面上的阴影长度越长.

图6
解析:作光路如图7所示,但解本题的困惑在于:入射角小于临界角C的入射光,折射角应小于90°,那折射光与地面的交点应在A点的右侧还是左侧?从图7分析似乎都是可以的,那(B)、(C)、(D)3选项便无法确定.其实,我们可以分析一些特殊光线,便可明确光路走向.我们来分析入射角趋向于0°的光线,其折射角也应趋向于0°,即光射向无穷远,因此说明入射角越小,射到地面上越远,因此照亮地面的区域应在A的右侧,阴影区域应A的左侧,正确光路为图7(a)所示.故(B)选项错误;而且n越小,临界角越大,阴影长度越长.故正确选项为(C).
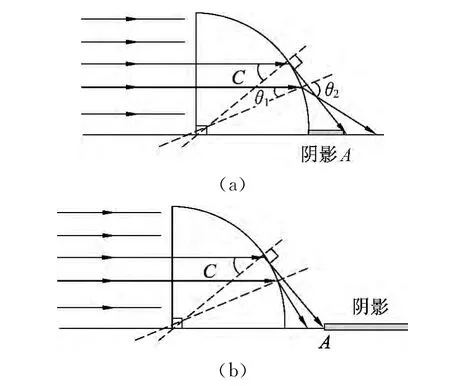
图7
思路点拨:一束光在传播时,其边界光线因处于特殊位置而成为我们关注的点.当涉及求光照范围或宽度等问题时,瞄准边界光线常常为我们快速解题打开方便之门.
4 定量分析,显现渐变过程
例4.一束由红、蓝两单色光组成的光线从一平板玻璃砖的上表面以入射角θ射入,穿过玻璃砖自下表面射出.已知该玻璃对红光的折射率为1.5.设红光与蓝光穿过玻璃砖所用的时间分别为t1和t2,则在θ从0°逐渐增大至90°的过程中
(A)t1始终大于t2.
(B)t1始终小于t2.
(C)t1先大于后小于t2.
(D)t1先小于后大于t2.
解析:作出光路图如图8所示,出射光线与入射光线平行,而且红光在玻璃中走过的路程长,但红光在玻璃中的传播速度也比蓝光大,因此在玻璃中的传播时间没法比较.当然,我们可以采用上例的方法,考虑特殊光线,当入射角为0°时,折射角也为0°,因此光走过的路程相同,则红光在玻璃中的传播时间小于蓝光的传播时间,但是否当入射角增大的过程中一直如此呢?仅对特殊光线的分析不能得到清晰的答案,因此我们必须定量分析,给出传播时间t关于入射角的函数表达式,然后进行比较.

图8
设入射角为θ1,折射角为θ2,玻璃砖的厚度为d,某一色光在玻璃中的折射率为n,因此光在玻璃中传播的时间为
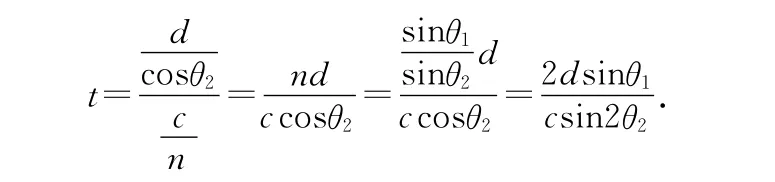
因为已知该玻璃对红光的折射率为1.5,当然玻璃对蓝光的折射率应大于1.5.因为由折射定律得sinθ1=nsinθ2.因为n>,所以θ2<45°,所以θ越大,sin2θ2越大.
对于同样的入射角,n越大,θ越小,时间就越长,因此在θ从0°逐渐增大至90°的过程中,红光的传播时间始终小于蓝光的传播时间,故(B)选项正确.
思路点拨:在几何光学中,经常研究某些极值或者两种色光比较等问题,我们可以写出所求量与变量之间的函数关系,利用函数的单调性和极值进行求解.

