随机变量序列部分和之和的完全收敛性

兰冲锋，吴群英

(1.阜阳师范学院 数学与计算科学学院，安徽 阜阳 236041；2.桂林理工大学 理学院，广西 桂林 541004）

0 引言

Resnick[1]以及Arnold[2]等在研究记录值之和的极限理论时，发现了有必要研究形如 的极限定理.而在实际问题中，如破产理论、随机游动以及时间序列分析理论中均有必要研究部分和之和的极限定理.基于此，苏淳，江涛[3，4]等研究了i.i.d.随机变量序列部分和之和的大数定律和中心极限定理；兰冲锋和吴群英[5]给出了i.i.d.随机变量序列部分和之和的完全收敛性的等价条件；宇世航[6～8]等将其推广到NA列，得到了部分和之和Tn的强、弱大数定律的条件，同时给出强平稳NA列部分和之和Tn的中心极限定理存在的条件.而对于更广泛的一般的随机变量序列部分和之和Tn的完全收敛性讨论,还未见文献记载。

许宝禄和Robbins[9]在1947年引入完全收敛性的概念以来，在i.i.d.情形下关于部分和Sn的完全收敛性最经典的结果应首推Baum和Katz[10]型定理，本文将在文献[5]的基础上，通过引入慢变化函数将i.i.d.随机变量序列部分和之和Tn的完全收敛性推广到一般的随机变量序列，以期随机变量序列部分和之和的极限定理作一个补充。

1 引理

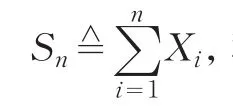
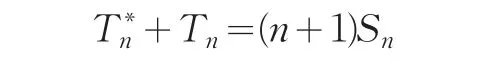
本文一律以“≪”表示通常的大“O”，以C记与n无关的正常数，在不同之处可以取不同的值.本文研究一般的更广泛的随机变量，设{Xn;n≥1}满足如下条件：

存在常数C，对任何单调函数f，若Varf(X1)＜∞,则有

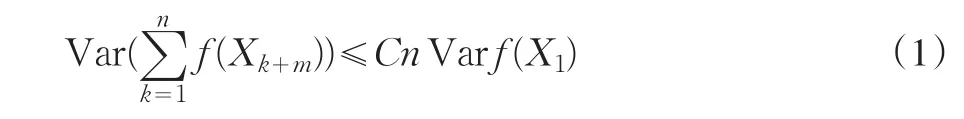
为证明本文的结论，先给出以下引理。

引理 1[11]假设g(a,k)是Xa+1,Xa+2,…,Xa+k的联合分布的泛函（a≥0,k≥1），满足

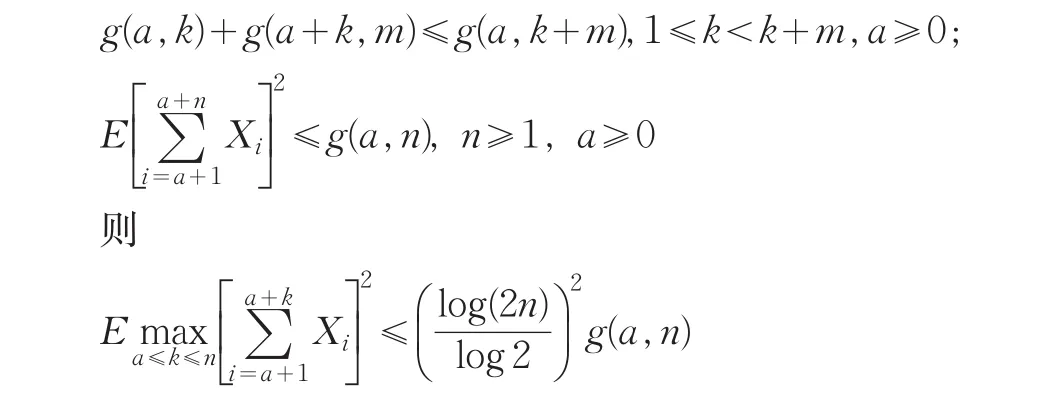
引理2设{Xn;n≥1}是同分布序列且满足条件（1.1）,对任何单调函数f，若Varf(X1)＜∞,有

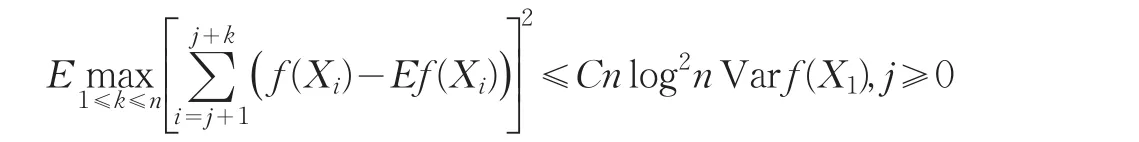
证：由条件（1）式得即得证。

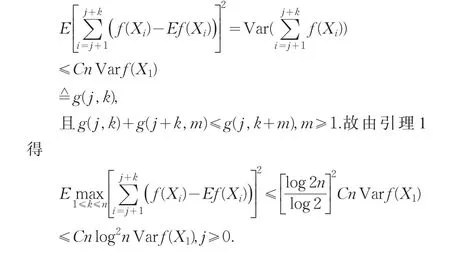
引理3[12]设{Xn;n≥1}是同分布序列且满足条件（1.1）,则对∀x≥0,有

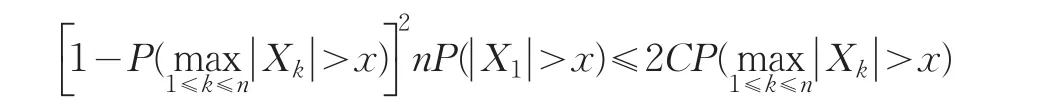
对于慢变化函数，有如下性质：如果l(x)＞0为x→+∞时的慢变化函数，则

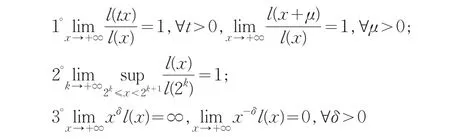
2 主要结果

定理1设{Xn;n≥1}是同分布随机变量序列且满足条件（1.1），αp＞1,p＜2,l(x)＞0为当x→+∞的单调不减慢变化函数，那么下列三式等价：

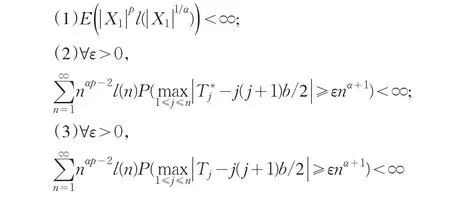
其中，b=0,若0＜p＜1；b=EX1，若1≤p＜2。

若{Xn;n≥1}是i.i.d.随机变量序列且取l(x)=1，此时显然条件（1）式成立，则有如下推论。

推论1：设{Xn;n≥1}是i.i.d.随机变量序列，αp＞1,p＜2,那么下列三式等价：

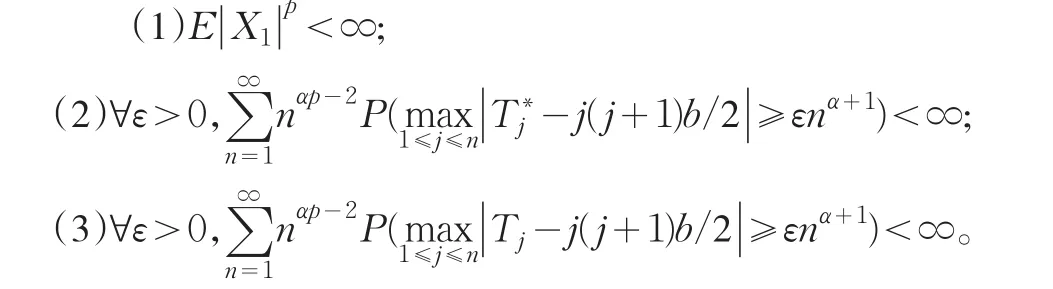
其中，b=0,若0＜p＜1；b=EX1，若1≤p＜2。

此推论即类似于著名的i.i.d.随机变量序列的Baum和Katz型完全收敛性定理。

在文献[5]中的我们曾经得到如下定理2。

定理2 设0＜p＜2，{Xn;n≥1}是i.i.d.r.v.序列，那么下列条件等价：

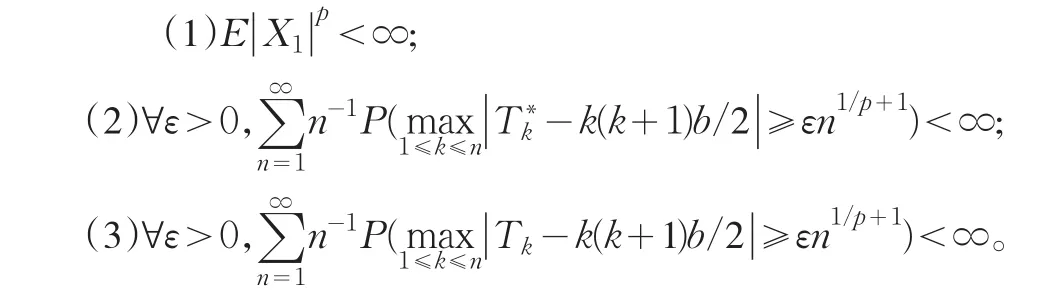
其中，b=0,若0＜p＜1；b=EX1，若1≤p＜2。

可见推论1的结论把文献[5]中定理2的条件由αp=1推广到了αp＞1的情形。

3 定理的证明

先证(1)⇒(2).对0≤a≤∞，记 f1(x)=f1(x,a)=(-a)∨(x∧a),x+=0∨x,x-=-(0∧x)，f2(x)=x-f1(x)，则 f1(x),f2(x),x+,x-都是x的单调函数，取q,使(1+1/αp)/2＜q＜1，令

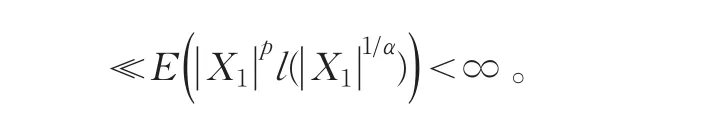
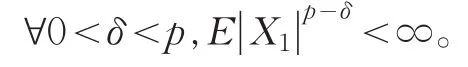
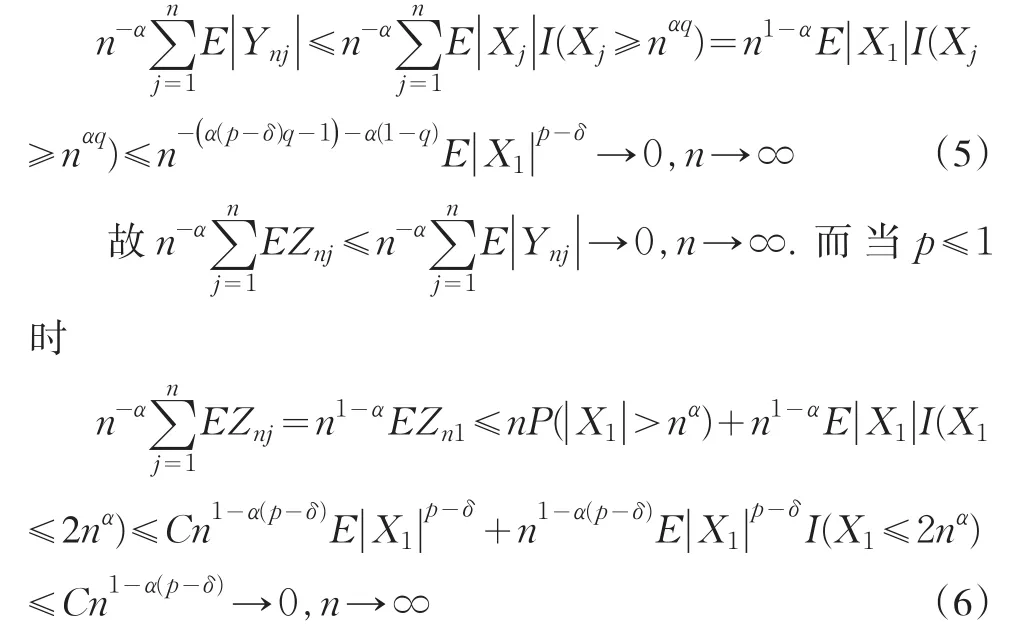
再由条件（1）式得

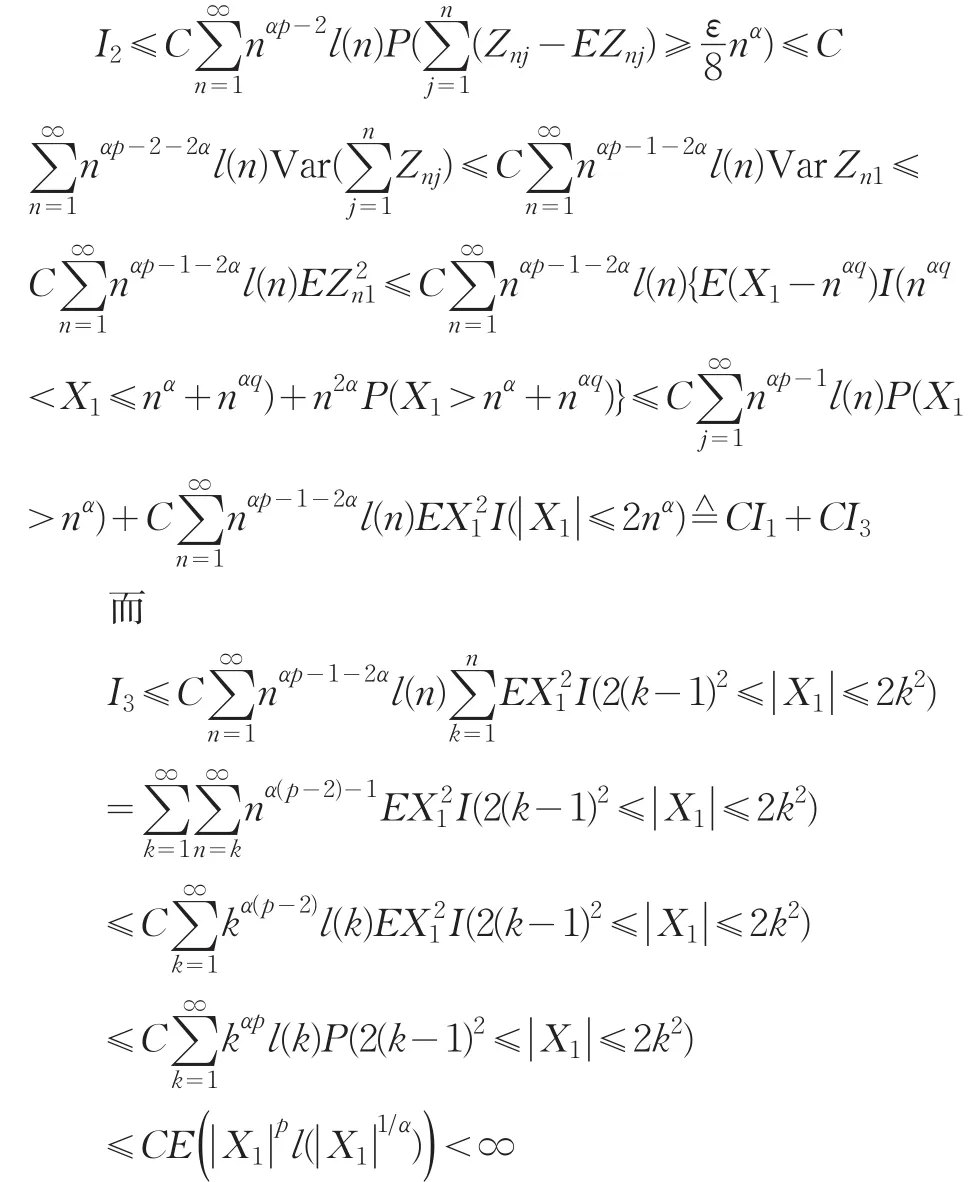
故I2＜∞。（2）得证。下证（4）成立,为此先证

当α≤1时，由αp＞1得p＞1。并注意EX1=0。由（5）得

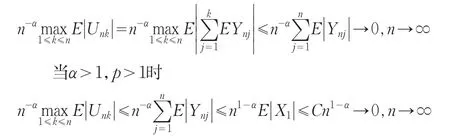
当α＞1，p≤1时，与（6）式类似地有

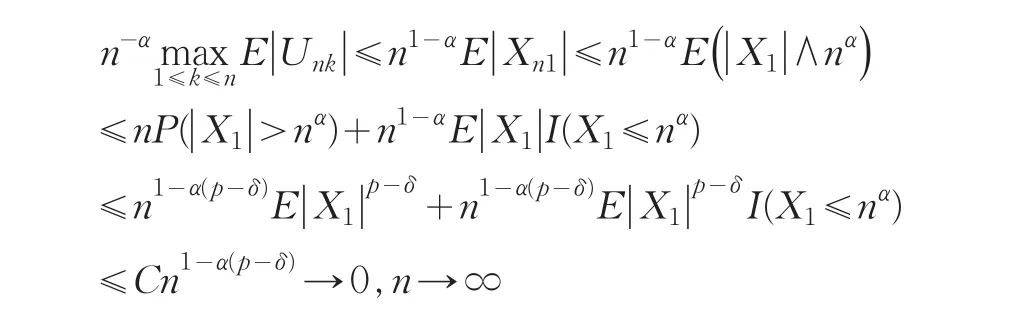
从而（7）式得证。

现取0＜δ＜p,使得2-p+δ＞0,qδ≤(2-p)(1-q),由（7）、引理2及条件（1）得

此即（2）成立。

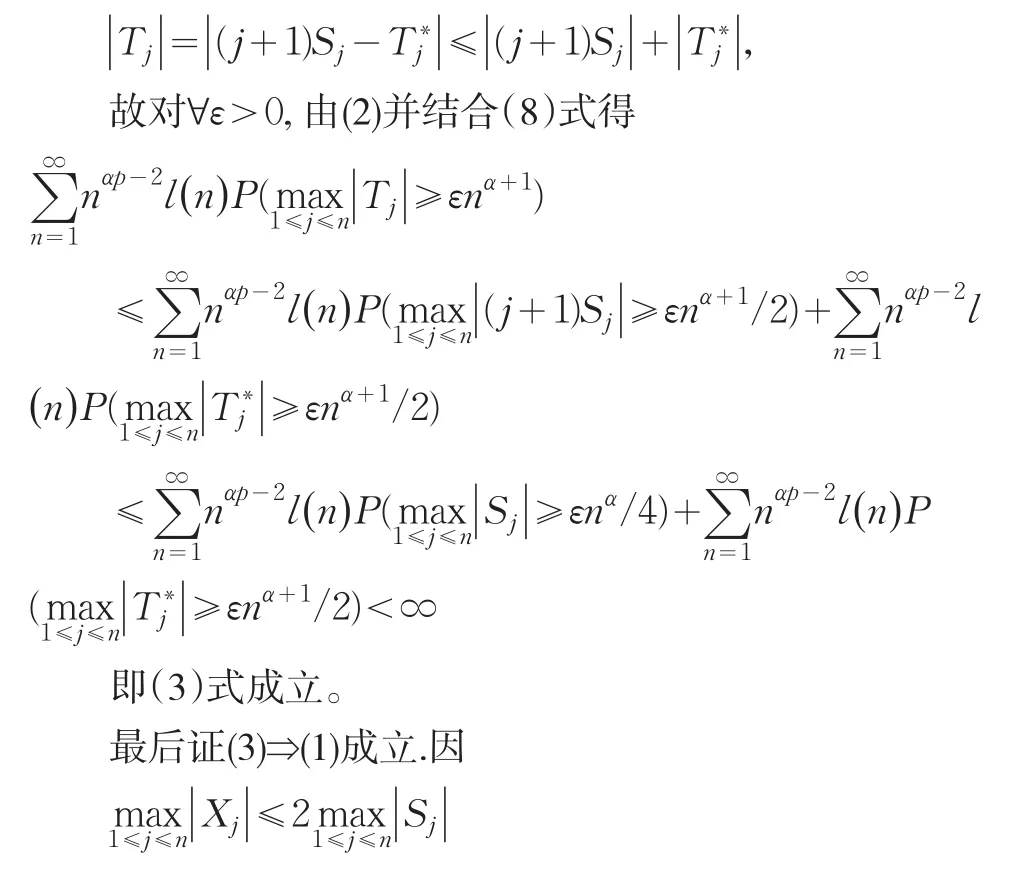
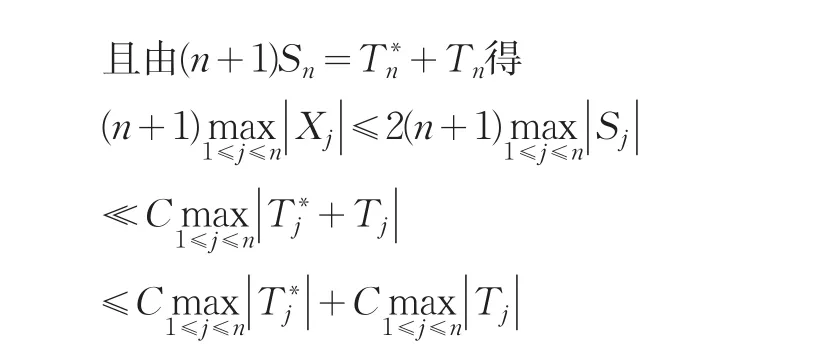
类比(2)⇒(3)的方式可以由（3）式推出（2）式成立.故由（2）式和（3）式可知

由上式并注意到αp-2＞-1,可知故（1）成立。证毕。

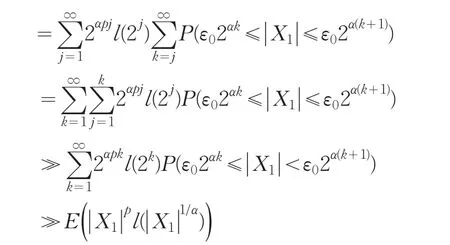
[1]Resnick S L.Limit Laws for Record Values[J].Stochastic Processes and Their Applications,1973,1(1).

[2]Arnold B C,Villasenor J A.The Asymptotic Distributions of Sums of Records[J].Extremes.，1998,1(3).

[3]江涛,苏淳,唐启鹤.I.I.D随机变量部分和之随机和的极限定理[J].中国科技大学学报,2001,31(4).

[4]江涛,林日其.I.I.D随机变量部分和之和的极限定理[J].淮南工业学院学报,2002,22(2).

[5]兰冲锋，吴群英.I.I.D.随机变量部分和之和的完全收敛性[J].吉林大学学报（理学版），2012,50(3).

[6]宇世航.同分布NA序列部分和之和的强大数定律[J].山东大学学报:理学版，2008，43（4）.

[7]宇世航.同分布NA序列部分和之和的弱大数定律[J].哈尔滨师范大学自然科学学报，2004，20（4）.

[8]宇世航,张锐梅.NA序列部分和之和的中心极限定理[J].高师理科学刊，2007，27（3）.

[9]Hsu P L,Robbins H.Complete Convergence and the Law of Large Numbers[J].Proc.Nat.Acad.Sci.USA,1947,（33）.

[10]Baum L E,Katz M.Convergence Rates in the Law of Large Numbers[J].Trars Amer.Math.Soc.,1965,(120).

[11]吴群英.混合序列的概率极限理论[M].北京：科学出版社，2006.

[12]张立新，王江峰.两两NQD序列的完全收敛性的一个注记[J].高校应用数学学报A辑，2004，19（2）.