具有纵向可比性的三维动态灰关联模型及其应用

赵 凯，门可佩，蒋 勇

(南京信息工程大学数学与统计学院，南京 210044)

0 引言

灰色系统理论是邓聚龙教授于1982年首先提出来的，其实质为对部分信息已知部分信息未知的系统的定量分析[1-3]。灰色关联分析[1,2]是灰色系统理论的两大基石之一，它并不深究系统的运行机制和物理模型，而是在距离空间与拓扑空间的基础上[4]，对系统的时间序列或截面数据建立关联分析模型，以量化系统运行状态。

目前常用的灰色关联度模型主要有：邓聚龙提出的邓氏灰关联度[1]，从曲线间的接近性或相似性来考虑量化；王清印的灰色B型关联度和C型关联度[5，6]，从位移、速度、加速度的角度来考虑量化；刘思峰的广义灰关联度[7]，从两条序列折线所夹的面积大小来考虑量化；李学全的灰色斜率关联度[8]主要从因素序列曲线的平均相对变化态势来考虑量化关联度。现有的计算模型的建立是基于充分考虑系统在发展过程中的相近性，全面考虑事物之间发展过程的异同性。但是，上述关联度模型给出的是静态的模型值，在纵向上变化发展的动态综合评价问题中，不同时间截面的关联度则不具有可比性。本文从纵向角度出发，给出一种具有动态可比性的三维灰关联模型，同时给出应用实例。

1 灰关联分析模型及其纵向可比性探讨

记评价系统为X={Xi=(xi(1),xi(2),...,xi(N))|i=0,1,2,...,m}，其中，m代表系统个数，N代表时间长度，并满足灰色关联四公理：

(1)规范性：0＜γ(X0,Xi)≤1，γ(X0,Xi)=1⇔Xi=aX0+b。

其中，i=1,2,...,m为评价序列的下标，a和b为常数。

(2)整体性：∀Xi,Xj(i≠j)∈X⇒γ(Xi,Xj)≠γ(Xj,Xi)。

(3)偶对称性：∀Xi,Xj(i≠j)∈X,γ(Xi,Xj)=γ(Xj,Xi)⇔X={Xi,Xj}。

(4)接近性：|X0(t)-Xi(t)|越小，则γ(X0(t),Xi(t))越大。

称无量纲数γ(X0,Xi)为系统Xi与参照系统X0之间的灰色关联度，γ(X0(t),Xi(t))为系统Xi与参照系统X0在t时刻的灰色关联系数。邓氏灰关联度定义为

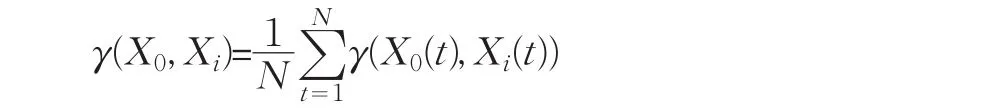
该定义默认系统行为序列是个一维时间序列，没有考虑动态多指标的问题。另外，在点关联系数有显著差异的情况下，邓氏灰关联度也有其缺陷，详见文献[9]。

按上面的定义，邓氏灰关联分析的计算步骤如下:

(1)确定参考序列和比较序列。在m个系统、N个时间长度的条件下，令参考序列与比较序列分别如下：

X0=(x0(1),x0(2),...,x0(N))，Xi=(xi(1),xi(2),...,xi(N))

(2)求各序列的初值像。为消除量纲的影响，设

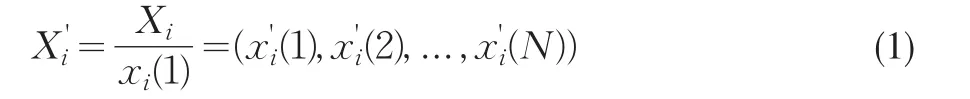
(3)求两级最大差和最小差。记

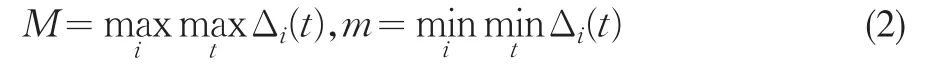
(4)求关联系数

其中，分辨系数ρ∈(0,1)，通常取ρ=0.5。

(5)计算关联度上述关联度的定义，是针对多系统、单指标的时间序列定量化评价问题。对于多系统、多指标的评价问题{xij(t)∈(Si,Xj,Tt)|i=0,1,2,...,m;j=1,2,...,n;t=1,2,...,N}，其中，m是系统的个数，n是评价指标的个数，N为时间长度，该评价问题的信息矩阵为

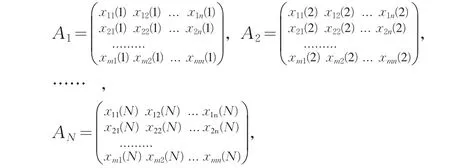
可以证明，对于上述动态评价问题，由(4)式定义的灰色关联度不具有纵向可比性。

但在应用灰色关联度进行动态多系统、多指标评价问题时，构造参考序列，使得该参考序列包含所有时间的信息，则所得的灰色关联度在横向和纵向上都具有可比性。

2 基于时间维度的参考序列选择及其关联度的可比性

对于多系统、多指标评价系统

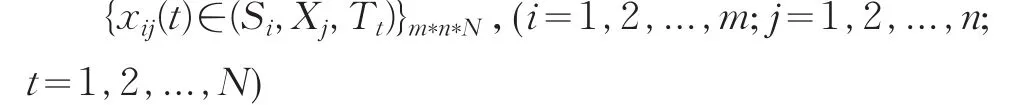
其不同时刻所有系统的信息矩阵为

(1)时间维度上的最大均值

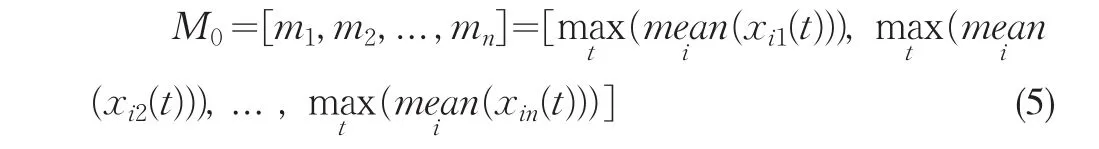
(2)数据无量纲化处理

(3)令动态参考序列为

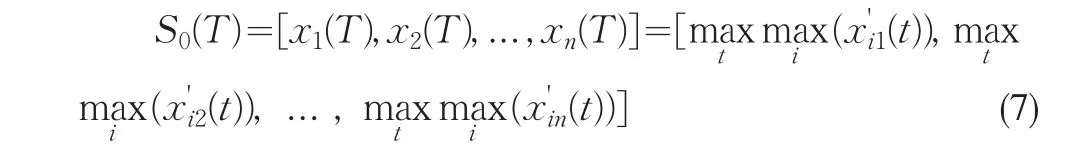
利用邓氏灰色关联度模型的(2)～(4)式，计算各个时间、各个系统与参考系统S0(T)之间的灰色关联度。由该方法计算出的关联度，不但继承了传统灰色关联模型可以横向比较的特性，而且还可以进行纵向比较分析，这在多系统、多指标、动态综合评价问题中可以取得很好的效果，同时也大大简化了计算。由于不同时刻各系统的信息矩阵已经进行过M0的均值化处理，所以无需再由(1)式对数据做无量纲化处理。

文献[11]给出的三维灰色关联模型，是对各个时刻的灰色关联度求均值，这是一个总体值，不同时刻的关联度仍然不能做纵向的比较。

3 应用实例

运用本文给出的新型灰色关联分析模型，对江苏省13个城市分别在“九五”末、“十五”末、“十一五”末的经济社会发展状况进行综合评价，也就是对2001、2006、2010年的运行状况进行综合评价，其评价系统为{xij(t)∈(Si,Xj,Tt)}13*5*3，系统信息、指标信息、时间信息和信息矩阵分别列于表1至表4所示。

表4给出2001、2006、2010年各个系统、各个指标经过本文定义的数据无量纲化后的数值，其具体趋势见图1至图3所示。经计算，时间维度上的最大均值序列为

M0=[m1,m2,m3,m4,m5]=[40054.270,37.900,80.543,390.886,131.520]；

其动态参考序列为

S0(T)=[x1(T),x2(T),x3(T),x4(T),x5(T)]=[1.792,3.523,4.199,3.116,7.656]。

表1 系统信息表

表2 指标信息表

表3 时间信息表

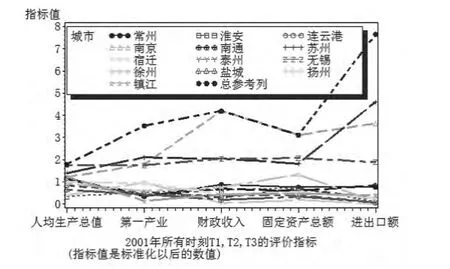
图1 2001年江苏各系统经过最大均值序列无量纲化后的状态

图2 2006年江苏各系统经过最大均值序列无量纲化后的状态

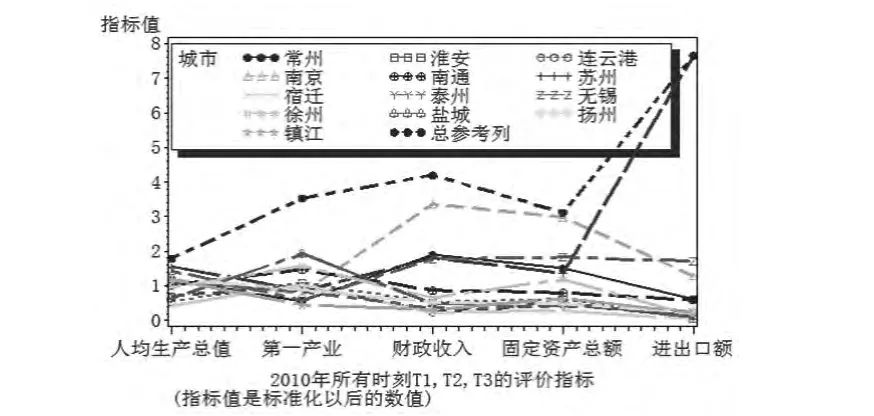
图3 2010年江苏各系统经过最大均值序列无量纲化后的状态

由(7)式得到的动态参考序列，结合(2)—(4)式则可计算出动态灰关联度值，如图4和图5所示。上述所求出的灰色关联度加入了时间信息，继承了传统灰色关联度的横向可比性，同时也具有纵向可比性。在考察系统与系统运行之间的相互关系的同时，可以考察同一系统在不同时间的运行状况。由图4，从时序纵向上比较灰色关联度，比如就苏州而言，2001、2006、2010年与动态参考序列的灰色关联度分别为0.7153、0.7639、0.7659，这说明苏州发展态势逐年提升，接近于参考系统的发展水平，而无锡则相反，徐州则有波动。从横向上比较灰色关联度，由图5可以看出，灰色关联度按照：＞2.0,(1.7,2.0),＜1.7的标准，可依次划分为三大方阵：第一方阵3个城市：南京、苏州、无锡；第二方阵6个城市：常州、淮安、南通、徐州、扬州、镇江；第三方阵4个城市：连云港、宿迁、泰州、盐城。该评价符合江苏经济社会发展的实际。

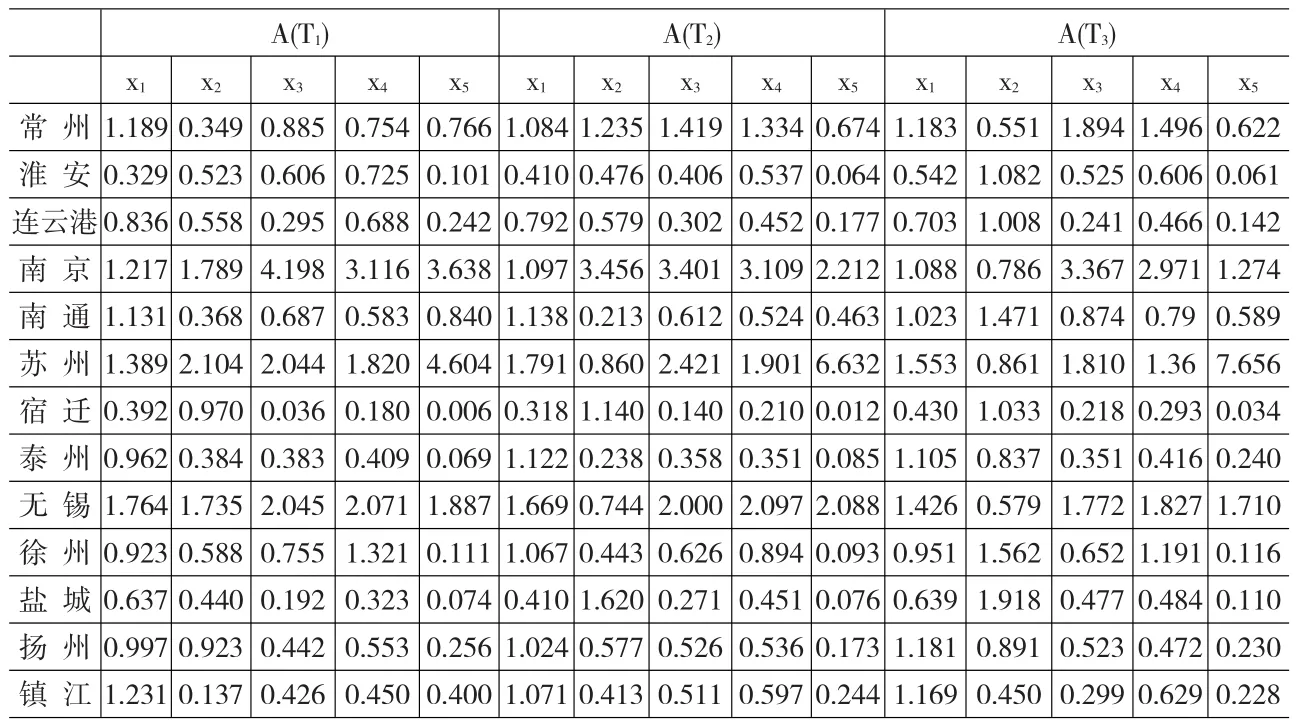
表4 经过M0无量纲化后的信息矩阵*

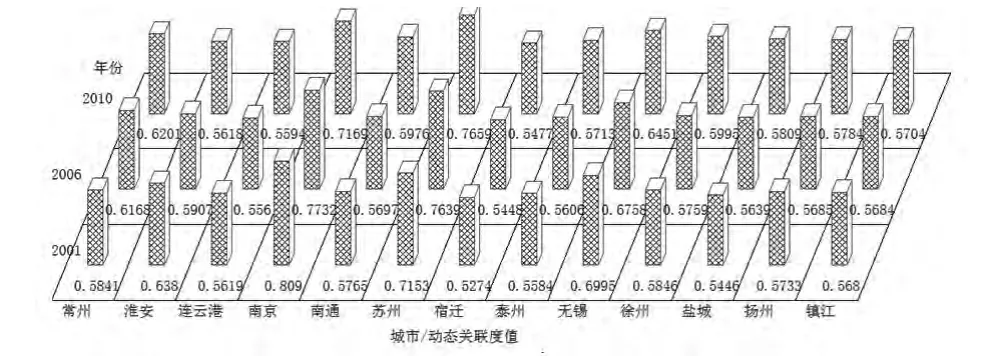
图4 2001、2006、2010年江苏13个城市与动态参考序列灰关联度

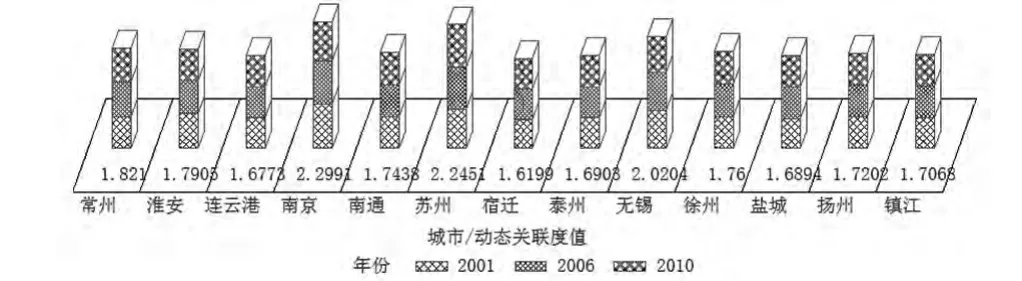
图6 江苏13个城市与动态参考序列灰关联度的3年总和

4 结论

本文在邓氏灰关联分析模型考虑多系统、单指标时间序列之间相关程度的基础上，构建三维动态多系统、多指标系统综合评价问题的灰关联度模型，其实质是在关于数据无量纲化处理的过程中，引入时间维度上的最大均值组M0=[m1,m2,...,mn]，并在选择动态参考序列S0(T)=[x1(T),x2(T),...,xn(T)]的时候引入时间维度，使得最后计算出来的灰色关联度同时具有横向和纵向的比较特性，可以更真实地反映系统的运行特点。相对于利用回归分析、主成份分析等方法而言，采用本文提出的基于动态参考序列的灰色关联度模型综合评价，其评价结果更为合理，失真度较小，且具有方便易行，计算量小等优点。因此，本文提出的方法不仅在社会经济统计等领域，而且在气象与空间统计领域也大有用武之地。

[1]邓聚龙.灰色控制系统[M].武汉:华中理工大学出版社,1995.

[2]邓聚龙.灰理论基础[M].武汉:华中理工大学出版社,2002.

[3]邓聚龙,党耀国,方志耕.灰色理论及其应用（第三版）[M].北京:科学出版社,2004.

[4]曹明霞,党耀国.灰色关联分析模型及其应用的研究[D].南京：南京航空航天大学硕士学位论文,2007.

[5]王清印.灰色B型关联分析[J].华中理工大学学报,1987,17(6).

[6]王清印,赵秀恒.C型关联分析[Z].华中理工大学学报,1999,27(3).

[7]Liu Sifeng.Generalized Degree of Grey Incidence[M].Information and Systems,Dalian DMU Publishing House,1992.

[8]李学全.灰色关联度模型的进一步研究[J].系统工程,1995,13(6).

[9]崔杰.点关联系数由显著性差异下灰色关联分析模型的改进[J].统计与决策,2008,(24).

[10]周亚,张骏.多属性决策中的TOPSIS法研究[D].武汉：武汉理工大学硕学位论文,2009.

[11]王正新,党耀国,沈春光.三维灰色关联模型及其应用[J].统计与决策,2011,(15).

[12]江苏省统计局.江苏统计年鉴（2002～2011）[M].北京:中国统计出版社,2002～2011.