引入二级贸易信贷政策和价格协商的集成存货模型

滕 颖

（浙江工商职业技术学院商学院，浙江 宁波 315010）

0 引言

传统库存模型一般会考虑买方或卖方总成本最小化。某些研究从供应链管理角度出发，将卖方和买方看作是一个整体，以做出双赢并且信息完全共享的生产或订购决策，进而实现总成本的最小化。Goyal最先提出最小化单一卖方和单一买方的总成本，Banerjee基于逐批订购法考虑了卖方生产率确定时该问题的求解，Goyal在放松Banerjee对逐批生产政策假设的情况下，考虑了卖方在单位生产运行中生产买方订单的整数倍问题。随后，其他很多学者也提出了同等订单量的集成卖方-买方模型。从以上研究可以发现，集成卖方-买方模型中卖方成本与卖方和买方的总成本均小于非集成卖方-买方模型中相应的成本；但买方成本却有所增加。基于互惠互利原则，卖方会采取一些激励策略来弥补买方损失，进而鼓励它们加强合作关系。其中一个方法是给到买方一定的价格折扣。

Teng和Chang在2009年通过对Teng和Goyal的研究进行扩展，在模型中引入了二阶信用政策。Chen和Kang在2007年提出了可允许延期支付的集成卖方-买方模型，该模型中需求具有确定性并给出了延长延迟期的处理过程以实现买卖双方储蓄的平衡。

在确立贸易双方的长期合作关系时，合作文化的某些因素在供应链管理中起着非常重要的作用，包括信任、相互性、信息交换、开放性和沟通等。Lee等提出供应链的有效合作关系须建立在信任与承诺的基础之上，互惠互利及信息共享对维持长期的稳定关系十分重要。贸易伙伴间开放性与广泛沟通的文化氛围可以增进彼此间的信任和信息共享，并加深对彼此的了解。在上述合作因素的接受性方面，本文通过考虑二阶信用交易政策放松了Chen和Kang在集成模型问题上的研究，从而构建了集成库存数学模型。为了使卖方价格适应买方价格，本文建立了谈判系统来达到双赢目的。特别是本文中的集成库存模型具有以下特征，即同时考虑了价格敏感需求的二阶信用交易政策和谈判系统。

1 变量界定与假设的提出

为便于开发模型和定理，本文使用以下符号，并做了如下假设。

符号定义：A表示买方每张订单的准备成本；S表示卖方每次生产运行的准备成本；F表示卖方处理每张订单的固定加工成本；rb表示买方除去利息费用外单位时间每单位储存成本率；rv表示卖方单位时间每单位储存成本率；v表示卖方单位商品的生产成本；c表示买方单位商品的采购成本；cd表示卖方实行谈判方案中的价格策略时买方的采购单价(cd=c-d,d＞0)；pbi表示在模型 i中(i=1,2,3)买方单位商品的售价(pbi＞c＞cd＞v)。D表示买方的年需求率，是关于买方售价的递减函数(D=,k＞0,β＞1)；w表示需求率(D)对生产率(P)的比率(P)，0＜w＜1；Ti表示在模型i中(i=1,2,3),买方每年的补充时间间隔期限；N表示买方所提供的付款期限；Id表示买方存款的年利率；Ic表示每美金存货需支付给银行的年利息费用；Iv表示用于计算延期付款给卖方所造成的机会利息损失的年利率；ni表示在模型i中(i=1,2,3)，卖方在生产运行期间买方的补充次数；TPBi(Ti,pbi)表示在模型i中(i=1,2,3)，买方每单位时间的利润总额(也表示为TPBi)；TPVi(Ti,ni,pbi)表示在模型i中(i=1,2,3)，卖方每单位时间的利润总额(也表示为TPVi)；TPi(Ti,ni,pbi)表示在模型i中(i=1,2,3)，由TPBi和TPVi相加所得的每单位时间的利润总额。

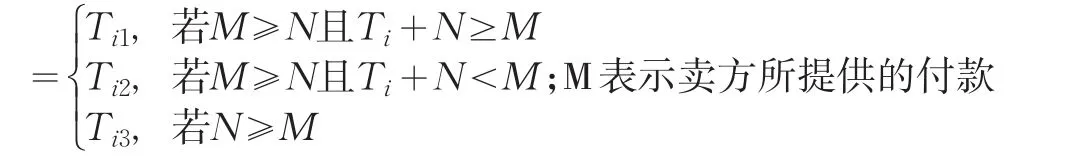
2 集成存货模型构建

为建立长期合作关系，将卖方与买方看作是一个统一体，买卖双方必须确定最优生产及订货策略以达到利润的最大化。基于这些考虑及假设，最后的客户需求对采购价十分敏感，并给出了集成卖方-买方模型的每单位时间的利润总额。以下将在T2、M和N的不同条件基础上确定模型中单位时间的利润总额。

2.1 模型构建

由上式可知，关于T2，TP21的二阶导数小于0，即

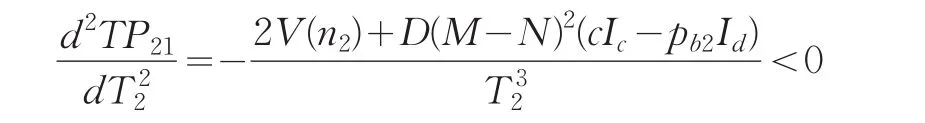
同样，固定n2，关于T2，TP22和TP23的一阶导数分别为

2.2 最优补充时间间隔

从以上各式可得到两种情况的最优补充时间间隔为

显然，TP2j,j=1,2,3是T2的凹函数，T2具有唯一最优解。

2.3 模型的解

在经营时，客户需求通常会随买方价格而发生变化。为增加利润总额，一个有效的方法就是确定买方最优定价。要做到这一点，本文给出了以下求解过程来确定最优价格、补充时间间隔以及买方订单每一生产运行的次数。求解过程包含两个部分。首先，给出了递归法来求解模型中两种情况的最优解，共产生了三个解集合；然后提出了从这三个解集合中挑选最优解的有效方法，来实现每单位时间利润总额的最大化。

3 数据实例

3.1 数据实例及参数设置

本节通过数例对该模型进行例证，其参数设置如下：A=100，c=5，rb=rv=0.1，S=1200，F=100，Id=Iv=0.02，Ic=0.06，v=2.5，k=300,000，β=1.245，w=0.8，M=0.1，e=0.01。此外，由于二阶信用交易政策对于N=0.0的设置将退化为一般的一阶政策，为便于问题的说明，将买方所提供的付款期限N设置成0.0或0.05。同样的，可将传统信用交易政策看作是本文模型的一个特例。

3.2 求解过程

步骤0：设置n0=1；

步骤1：对于j=1,2,3；

压力容器支座是在主梁上支撑罐体的主要部件，将支撑垫板、支座和连接块作为一个焊接组合体来考虑在观察各部件变形的同时也可观察到焊接部位的受力情况，方便对整体的把握。图13所示的是追尾车辆与车架开始碰撞瞬间组合体整体的应力云图，经过观察碰撞动画与应力的动态关系，发现组合体此时所受的应力是最大的，故主要研究组合体此时的应力形变。

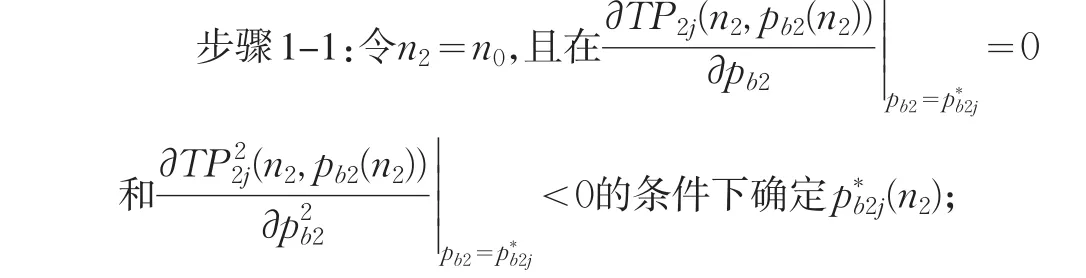
步骤2：将步骤1中的三个解集合代入，就可找到最优解，进而获得以下每单位时间的最大利润总额。对于M≥N，若，则每单位时间的最大利润总额可确定为否则，设置同样地，若，则每单位时间的最大利润总额可确定为否则，设置

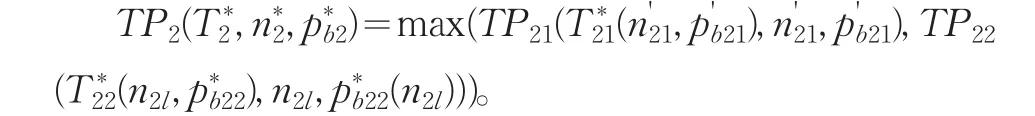
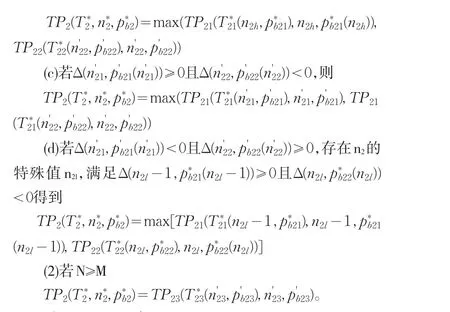
3.3 实验结果及分析

表1基于求解过程和价格谈判系统列出了带有谈判因子a(a=1)的模型的最优解。对于N=0.0，与非集成模型相比，集成卖方-买方模型的每单位时间的利润总额增加了5.0%(PTPG2)。表1也显示了当实行谈判系统时PTPG3通过0.14%的增量增加到5.16%。对于N=0.05，表1表示这三种模型对二阶信用交易政策的应用与N=0.0时的结果相似。

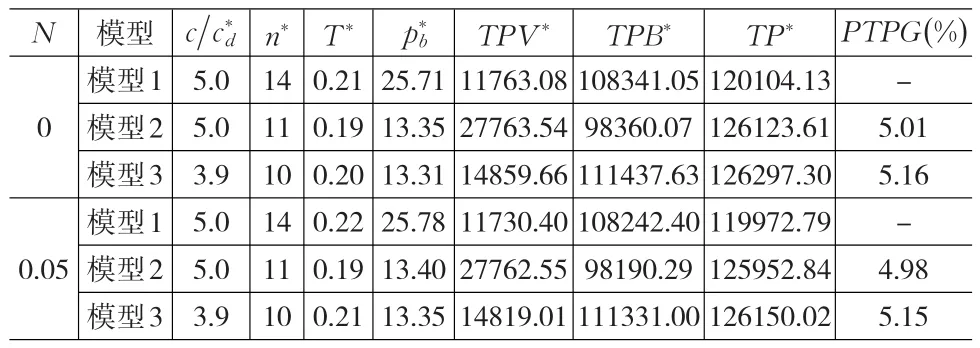
表1 需求量对pb敏感且客户具有不同付款期限的三种模型的最优解

通过实行谈判方案，对关于谈判因子a的最优解进行敏感度分析。基于VI=α×BI，当N=0时，来自该集成的总收益增量必定属于买方，其中α=0，BI=6236.98。换而言之，α值越大，卖方的利润越多。α值的增加将使得买方每单位采购成本和每单位售价稍高。α值的减小会使总利润率(GMR)增加，这样有利于买方。因此，α值大于1时对卖方有利。此外，当考虑买卖双方的谈判时PTPG会不断增加。关于N=0.05的二阶信用交易政策，在不同的α值下会产生相似的结果。另外，买卖双方的利润总额和PTPG的各项指标略小于N=0.0时的相应指标；但是，由于二阶信用交易政策的应用，买方每单位的采购成本、每单位售价及总利润率却相反。

4 结论

本文放松了Chen和Kang对客户需求确定性的假设，在集成模型中基于对价格敏感需求及买方向客户提供付款期限的考虑，客户必须在购买商品时付清货款，这被称为二阶信用交易政策。文中这类考虑在已有文献中的研究较少。考虑到二阶信用交易政策，我们指出，买方的最优定价、补充时间间隔和买方订单的每生产运行次数均有唯一解。为了确定集成模型中的最优解，提出了递归求解过程。由于合作关系对买方不利，为了弥补买方的损失，通过考虑卖方向买方提供一定的价格折扣，给出了谈判系统。建立价格谈判程序来确定买卖双方的最优定价、订购/生产战略等。考虑到传统及二阶信用交易政策，我们通过数例对该模型进行了说明，并对谈判因子进行了敏感度分析，从而研究了买方和卖方的利润总额、PTPG、买方售价、卖方价格(买方的采购成本)、买方总利润率等的变化。

从实证中可以获得以下结果。如谈判方案所设计的，当谈判因子a增加时，买方(卖方)的利润总额会减少(增加)。当应用二阶信用交易政策时(数例中M=0.1，N=0.05)，买方和卖方的利润总额比使用传统信用交易政策(M=0.1，N=0.0)时的利润总额略小，而无论谈判因子α的值多大，买方的每单位售价每单位采购成本和总利润率却刚好相反。虽然M=0.1，N=0.05时的比M=0.1，N=0.0时的大些，但买卖双方的利润总额却减少了，主要原因是利息收益和总需求量减少了。尽管如此，对于M=0.1，N=0.0和M=0.1，N=0.05这两种情况，虽然卖方会向买方提供一定的价格折扣，但集成模型的利润总额还是会通过谈判系统增加。

本文在对其它合作因素(如信任、开放性和沟通等)进行假设的前提下，考虑了集成模型中贸易双方间的互惠互利、信息共享等问题，因此，不需要考虑机会主义行为的风险。在未来的研究中，需要对所有合作因素进行进一步的研究，进而研究集成库存模型在实际应用中引入这些因素的方法。另外，跨职能合作问题在供应链问题中十分重要，进一步研究该问题可以实现集成模型的公式化。

[1]Abad,P.L.,Jaggi,C.K.A Joint Approach for Setting Unit Price and the Length of the Credit Period for Seller when End Demand is Price Sensitive[J].International Journal of Production Economics,2003,83.

[2]Barratt,M.Understanding the Meaning of Collaboration in the Supply Chain[J].Supply Chain Management,2004,9(1).

[3]Chang,H.C.,Ouyang,L.Y.Wu,K.S.,Ho,C.H.Integrated Vendor-buyer Cooperative Inventory Models with Controllable Lead Time and Ordering Cost Reduction[J].European Journal of Operational Research,2006,170.

[4]Chen,L.H.,Kang,F.S.Integrated Vendor-buyer Cooperative Inventory Models with Variant Permissible Delay in Payments[J].European Journal of Operational Research,2007,183.

[5]Jaggi,C.K.,Goyal,S.K.Goel,S.K.Retailer,s Optimal Replenishment Decisions with Credit-linked Demand under Permissible Delay in Payments[J].European Journal of Operational Research,2008,190.

[6]Ouyang,L.Y.,Wu,K.S.,Ho,C.H.Integrated Vendor-buyer Cooperative Models with Stochastic Demand in Controllable Lead Time[J].International Journal of Production Economics,2004,92.

[7]Ouyang,L.Y.,Ho,C.H.Su,C.H.,Optimal Strategy for an Integrated System with Variable Production Rate when the Freight Rate and Trade Credit are Both Linked to the Order Quantity[J].International Journal of Production Economics,2008,115.