基于改进模拟退火算法的模糊回归参数估计

彭宇文，郭莉莎，毛 超

（1.湖南师范大学 商学院，长沙 410000；2.湖南大学 工商管理学院，长沙 410082）

0 引言

在现实生活中，统计对象的某些特性使得一些统计数据往往难以准确的记录或收集。例如，在测量河流水位高低时，会由于波浪使水位在一定范围内波动，而不是停留在某个具体的数值上，样本数据具有一定的模糊性。在研究对象的观测值具有模糊性时，模糊集理论成为重要的方法。Zadeh(1965)首次提出了模糊集理论[1]，Tanaka等(1982)在此基础上，提出了模糊数据回归问题。模糊回归在许多领域得到了广泛的应用[2]。

国内外对模糊回归的研究包括对线性和非线性回归模型的研究，总体上可分为三类：第一类是变量之间关系是具有模糊性，即需求解的回归系数是模糊的；第二类是因变量、自变量中的部分或者全部具有模糊性，即变量本身具有模糊性；第三类是变量与系数均具有模糊性。由于第三类较复杂，大多数研究集中在第一类和第二类。

第一类和第二类模糊回归问题是第三类模糊回归问题的特殊情形，因此，探索更具一般性的模糊回归方法具有重要意义。本文讨论第三类模糊回归问题的参数估计，其变量与系数均具有模糊性的回归模型。

1 模糊回归模型

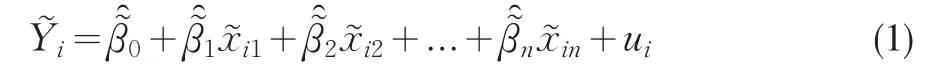
非线性回归的目标是对下述模糊非线性模型的参数进行估计：

模糊非线性回归模型可通过取对数转化为模糊线性规划模型如下：

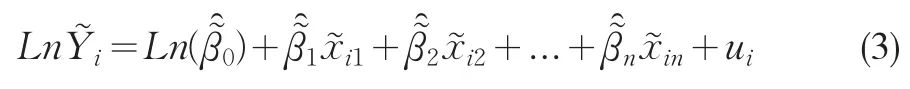
2 基于模拟退火算法的模糊回归参数估计

2.1 拟合效果的评价

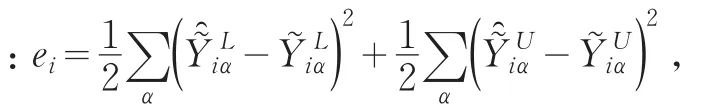
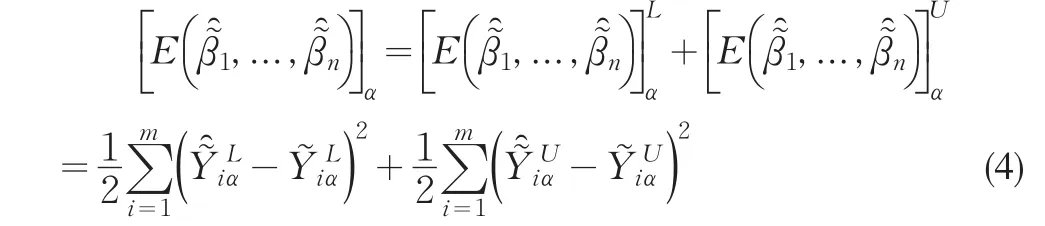
与隶属度关联的总误差可以表示为：

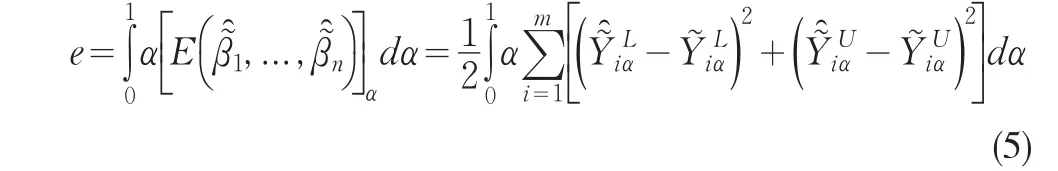
为简化运算，将(8)式改写为离散形式并将样本值代入，可得：

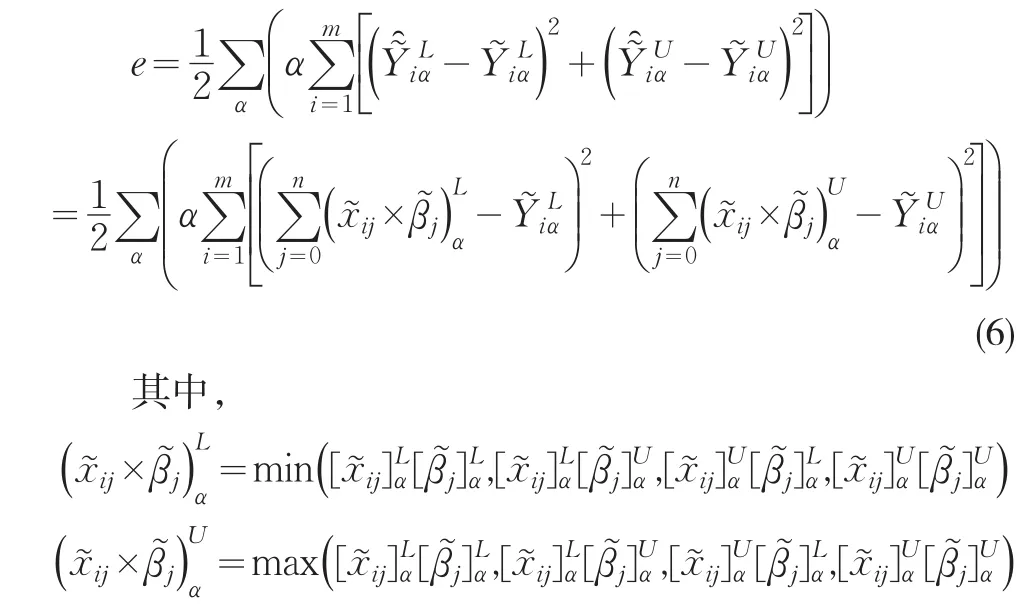
2.2 算法设计

式(6)的最小值是一个无约束二次函数最值问题，但由于模糊运算的复杂性，无法直接求出其最优解。采用启发式算法进行求解成为重要思路，模拟退火算法具有对初始可行解要求低，通过Metropolis接受准则避免陷入局部最优等优点[5]，本文对传统模拟退火算法进行改进以获得最佳的参数估计值。

(1)算法流程。参数估计的模拟退火算法具体步骤为：

①获取一个初始可行解x0=，设定初始温度t0，令当前解xi=x0，当前迭代步数k=0，当前温度tk=t0。

②若在该温度达到内循环停止条件，则转第③步；否则，从邻域N(xi)中随机选择一个邻解xj，并计算两个解对应的拟合效果之差ΔEij=E(xj)-E(xi)。若ΔEij≤0，则 xi=xj；否则，若 exp(-ΔEij/t)＞rand(0,1)(rand(0,1)表示一个0到1之间的均匀随机数)，则xi=xj，重复第②步。

③k=k+1，tk+1=y(tk)(温度控制函数)，若满足终止条件，转第④步；否则，转第（2）步。

④输出计算结果，算法停止。

内循环为第②步，它表示在同一个温度下进行随机搜索。外循环主要包括第③步的温度下降变化，迭代步数的增加和停止准则。

(2)初始解的构造。为获得初始解，本文用所有模糊样本的左边界、右边界、以及隶属度为1时的样本取值分别进行回归，将各参数的回归系数中的最小值作为模糊系数的左边界，最大值作为模糊系数的右边界，中间值作为模糊系数隶属度为1时的值。

(3)邻域操作。为获得更优的解，设计了多层次邻域操作方法。以三角模糊数为例，各参数的形式为首先，随机选取个系数作为需要调整的对象；其次，N个对象分别随机选定中的一个作为要调整的部分；最后，确定需要调整的幅度：若调整，则调整的幅度为否则，调整幅度为其中，K的取值与的数量级相关，K由小到大依次确定解的粗调整、二次调整和微调整的幅度。可根据试探性运算的结果，确定k1值，使得当连续k1次目标函数值得不到改善时，改变K的取值，进入下一层邻域操作。其他类型的模糊数同样可按此思路进行多层次邻域操作。

(4)终止准则与结果输出。采用双终止准则，第一，完成三层邻域操作后，仍然出现了连续k2次目标函数值得不到改善，则终止程序，输出结果；第二，温度t下降到预先设定的某个值，则终止程序，输出结果。为获得该次运算的最优结果，在外循环中增加变量记录每次目标函数得到了改进的解。

3 算例及结果分析

3.1 算例分析

为了说明拟合效果评价方法与求解算法的有效性，采用文献[6]的算例作为模糊线性回归算例，对文献[4]的模糊非线性规划算例的自变量模糊化，作为模糊非线性回归算例。

3.1.1 线性回归算例

文献[6]设计的算例具有一个模糊因变量和两个模糊自变量，共有15对样本。采用本文的算法求解时，算法参数的设定对结果的优劣有一定的影响，本文通过多次调整和运算来获取相对最佳参数，对模拟退火算法参数设定如下：马尔科夫链长度取200，初始温度取100，衰减因子为0.98。 K 值依次取500、1000、1500。初始解取：x0=((3 .0450,3.6524,4.0531),(0 .4937,0.4970,0.4986),(0.0089,0.0092,0.0097))。求解得到的模糊线性回归方程为如下：

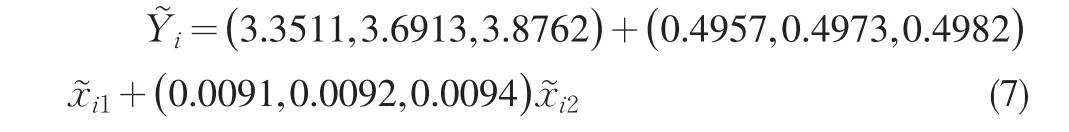
图1为退火过程，图2对拟合值与样本值进行了比较。

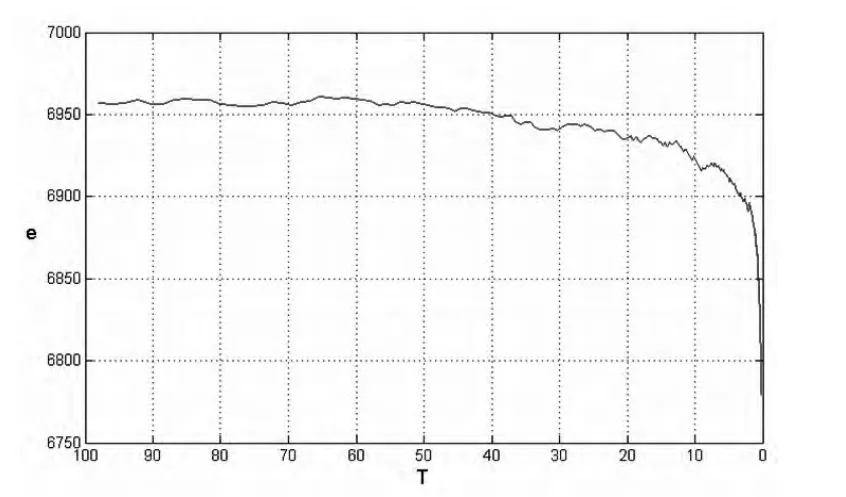
图1 算例1的退火图

图2 算例1的样本值与拟合值比较

3.1.2 非线性回归算例

对文献[4]的模糊非线性规划算例的自变量进行模糊化，得到模糊非线性回归样本值如表2。

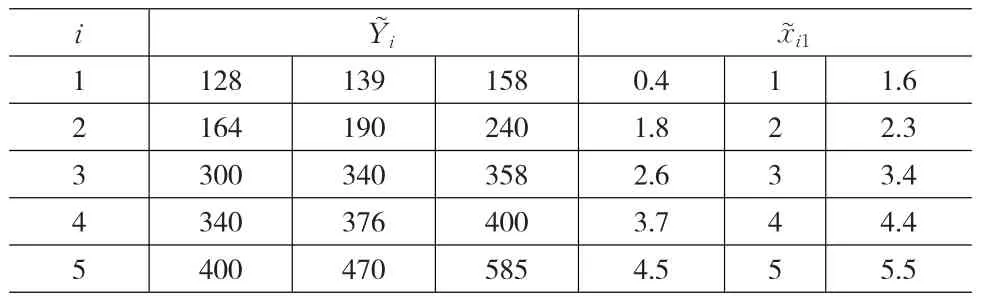
表2 模糊非线性回归样本值

调用模拟退火算法，马尔科夫链长度取200，初始温度取100，衰减因子为0.98。 K 值依次取100、500、1000。分别对左边界、中间值和右边界进行非线性回归，得到初始解：x0=((118.6336,124.0292,)125.8052,(0.2679,0.2705,0.2895))。

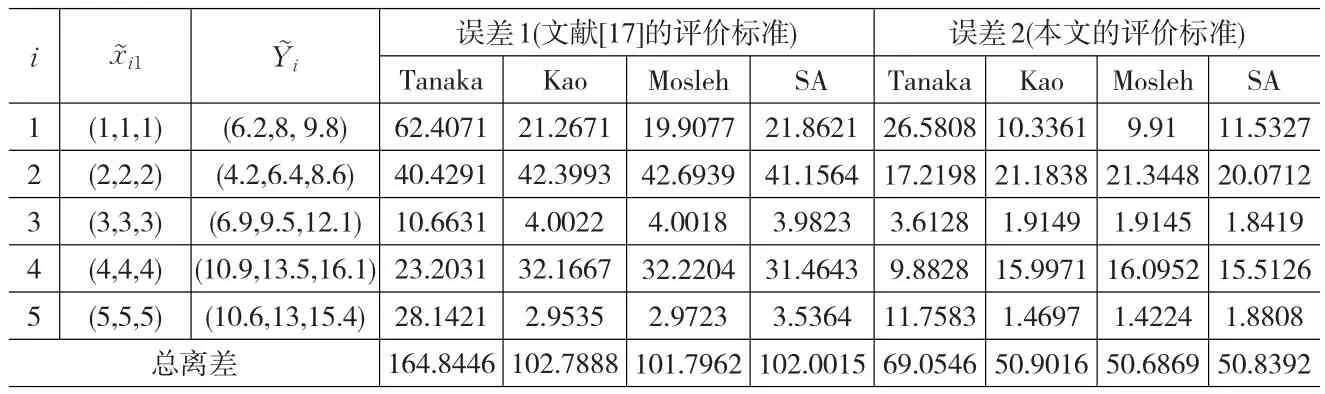
表3 不同模糊回归方法的比较

求解得到的模糊线性回归方程如下：

图3对拟合值与样本值进行了比较。

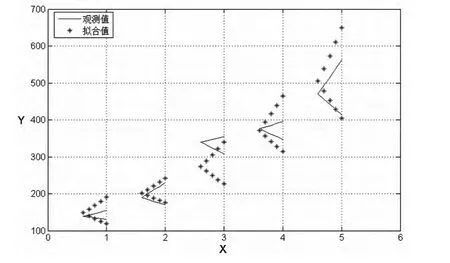
图3 算例2的样本值与拟合值比较

3.2 比较分析

本文采用 Tanaka等(1989)、Kao等(2003)、Mosleh 等(2010)共同用来说明各自模糊回归方法的算例进行比较分析[4,7,8]。算例与计算结果见表3。

Tanaka等(1989)的最终回归方程为：

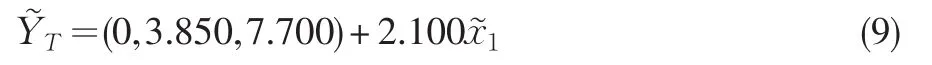
Kao等(2003)的最终回归方程为：

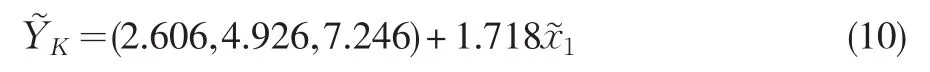
Mosleh等(2010)采用神经网络方法获得的最终回归方程为：

各种方法的拟合效果比较见图4。

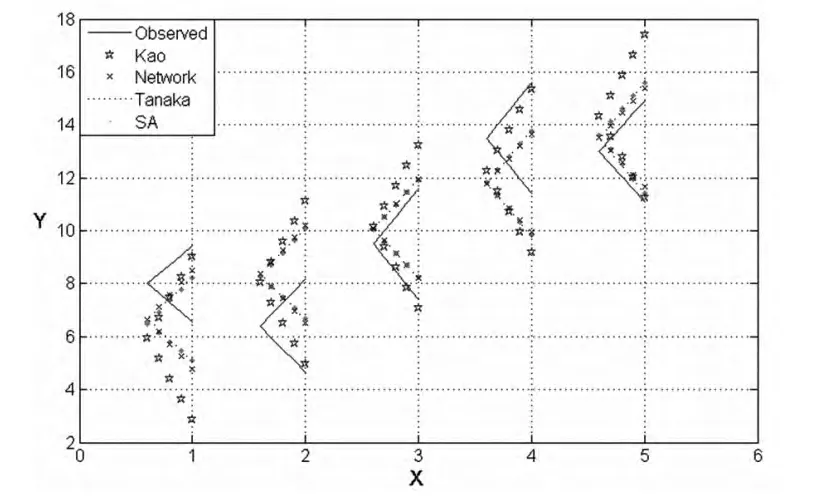
图4 Tanaka方法、Kao方法、Mosleh方法与SA方法的拟合效果

从图4可以看出，基于多层次邻域操作的模拟退火算法的模糊回归方法拟合效果要优于Tanaka等(1989)、Kao等(2003)的方法，非常接近Mosleh等(2010)的方法。Mosleh等(2010)是通过构造模糊神经网络，采用的梯度下降法进行求解的，虽然其结果较好，但其计算过程只适用于三角模糊数以及输入为精确数的模糊回归模型。而本文的方法可在获得近似最优解的前提下，处理各种类型的模糊数据以及输入、输出和系数均为模糊数的回归模型。

4 结论

模糊回归分析是分析模糊数据之间关系的一种有效方法，其在处理一些无法获得精确数，只能得到可能性数据的对象时发挥了重要作用。本文考虑了模糊数据的回归中不同隶属度下误差的模糊性，认为不同隶属度下的误差对总误差的贡献不同，提出了与隶属度关联的拟合效果评价方法。从启发式算法入手，采用模拟退火算法并进行相应的改进，达到了在获得近似最优解的前提下，克服了以往仅考虑系数和变量中的一种具有模糊性的局限性，给出了能处理各类模糊观测值以及系数和变量均具模糊性的线性和非线性回归模型的启发式求解思路。对拟合系数显著性的检验、模糊回归与时间序列分析的融合以及模糊样条回归方法等是模糊回归的进一步研究方向。

[1]Zadeh L.A.Fuzzy Sets[J].Information and Control,1965,8(3).

[2]Tanaka H,Uejima S,Asia K.Linear Regression Analysis with Fuzzy Model[J].Ieee Trans.Sys.Man and Cyber.Smc.,1982,12(6).

[3]李竹渝,张成.模糊数据的回归模型结构分析[J].统计研究,2008,25(8).

[4]M.Mosleha,M.Otadi,S.Abbasbandyb.Evaluation of Fuzzy Regression Models by Fuzzy Neural Network[J].Journal of Computational and Applied Mathematics,2010,234(3).

[5]康立山,谢云,尤矢勇等.非数值并行计算,模拟退火算法(第一册)[M].北京:科学出版社,1997.

[6]Hsien-Chung Wu.Fuzzy Estimates of Regression Parameters in linear Regression Models for Imprecise Input and Output Data[J].Computational Statistics&Data Analysis,2003,42(1～2).

[7]H.Tanaka,I.Hayashi,J.Watada.Possibilistic Linear Regression Analysis for Fuzzy Data[J].European Journal of Operational Research,1989,40(3).

[8]C.Kao,C.L.Chyu.Least-squares Estimates in Fuzzy Regression Analysis[J].European Journal of Operational Research,2003,148(2).