Kemeny社会选择函数的0-1规划算法
吴祥标
(遵义师范学院数学与计算科学学院,贵州遵义563002)
Kemeny社会选择函数的0-1规划算法
吴祥标
(遵义师范学院数学与计算科学学院,贵州遵义563002)
Kemeny函数是群决策中的一种社会选择函数,作者将Kemeny函数的计算过程转化成整数规划模型的求解,并提出了一种有效的算法。
Kemeny函数;社会选择函数;群决策;整数规划
群决策中的Kemeny函数是J GKemeny(1972)提出的一种社会选择函数,这种社会选择函数要使社会的排序与投票人对各方案的偏好序有最大的一致性。Kemeny函数为所有方案的每一个可能的排序赋予一个函数值来表示该排序与投票人的个体排序之间的一致性,并将最大的函数值所对应的排序作为群的排序。
当方案的比较多时,用穷举法计算量太大。穷举法不是一种有效的算法,因此提出了计算Kemeny函数的0-1规划算法。
1 Kemeny函数
为了方便表述,先引入如下符号:
N={1,2,…,n}表示群,即投票人的集合;
A={a1,a2,…,am}表示备选方案(候选人)集合;
njk或表示群中认为aj优于ak的成员数。
采用上述标记,过半数规则可以表示为:对aj,ak∈A,若njk>nkj,则;若njk=nkj,则ajGak。
Kemeny函数的计算过程分为以下几个步骤:
社会选择的排序矩阵L={ljk},j,k=1,2…m,其中上的线性序都有相应的矩阵。
(3)计算Kemeny函数
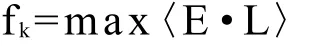
2 Kemeny函数算法的分析
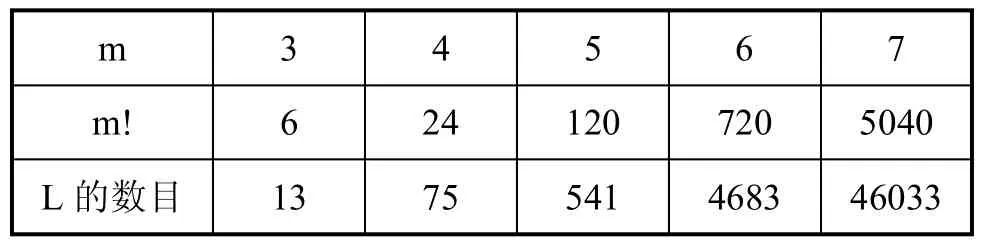
表1 m=3~7时L的数目
从上表可以看出,利用Kemeny函数进行群决策最大的困难是计算量较大。因此,有必要对Kemeny函数的算法进行一些改进。
定理1一定存在一个传递的强序,使得Kemeny函数取得极大值。
按照步骤一,得到新的排序的Kemeny函数值fk=〈E·L〉+ejk,因而有〈E·L〉≤〈E·L0〉。
所有传递的强序矩阵中的Kemeny函数的值最大的排序矩阵,则这个排序可以使得Kemeny函数取得最大值。证毕。
由定理1可以知道,我们只需要对传递的强排序进行比较,就能找出最优的排序。对于存在无差异关系的情况,会在本文的后面进行讨论。
3 整数规划算法
(1)ljk∈{-1,1}, j≠k
(2)ljk=-lkj,j,k
(3)-1≤lhj+ljk+lkh≤1,h≠j≠k
条件(1)和(2)很清楚,条件(3)可以保证传递性的需要。若ah,aj,ak非传递,必有lhj,ljk,lkh同号,则lhj+ ljk+lkh=-3或lhj+ljk+lkh=3。ah,aj,ak满足传递性,则lhj+ljk+lkh=-1或lhj+ljk+lkh=1,由于lhj,ljk,lkh都为奇数,所以约束条件(3)能保证满足传递性。

(1)ljk∈{-1,1}, j≠k
(2)-1≤lhj+ljk-lhk≤1h<j<k
Kemeny函数可用如下整数模型求解:
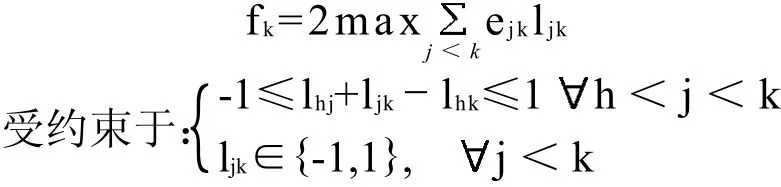
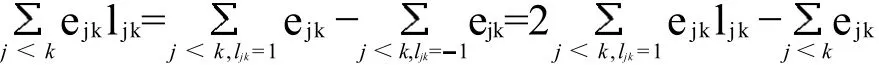
令L=ljk,其中
(1)ljk∈{0,1},≠
(2)ljk+lkj=1,j,k
(3)lhj+ljk+lkh≤2,h,j,k
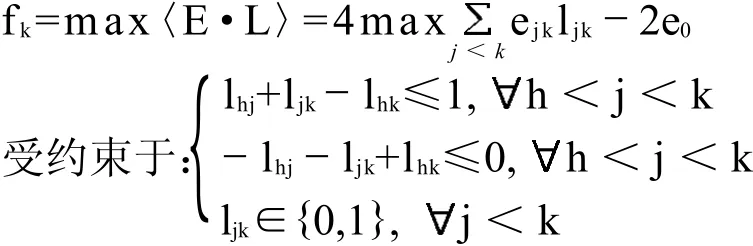
4 关于无差异的分析
在群决策中,如果只存在两个方案,而支持这两个的相同,我们认为这两个方案是无差异的。那么,在存在多个方案时,会不会存在这种无差异的情况呢?
比如某个群对三个备选方案a,b,c进行排序,群中成员可能会有如下6种观点:
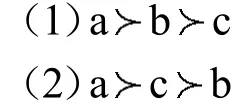
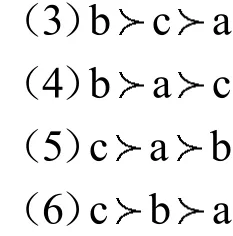
假设群中有六个成员,分别支持以上6种观点,或者2个支持观点(1)、2个支持观点(2)、2个支持观点(3)。群中各成员的权力相同,因此很难确定方案a,b,c的优劣次序,在这两种情形下,我们有理由认为方案a,b,c是无差异的。
同样,用Kemeny社会选择函数得出的社会总体排序也会出现这样的无差异关系。在前文中,为了减少计算量,我们忽略了含有无差异关系的社会排序,但是无差异关系是存在的。例如,在某个群决策中,排序矩阵使得Kemeny函数取得极大值。假设在这个排序中,排在第 位和第 +1位的方案分别为ai和ai+1,且两两比较的结果是ai≈Gai+1。则将排序矩阵L中aiGai+1变成ai≈Gai+1其它排序保持不变的得到的新的排序矩阵L0。排序矩阵0也使得Kemeny函数取得极大值,因此我们认为方案 和 是无差异的。
用整数规划算法求解时,如果最优解不唯一,说明社会排序存在无差异关系。若排序和排序…(i<j)都能使得Kemeny函数取得极大值,则可以认为方案ai,ai+1,…, aj-1,aj是无差异的,因为排序也能使得Kemeny函数取得极大值。
5 示例
示例1参考文献[1]中的例11.6
投票矩阵为:
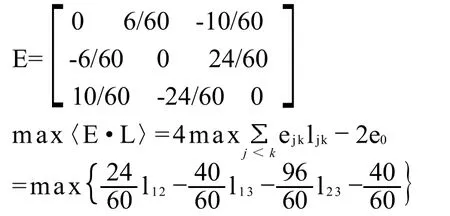
受约束于:
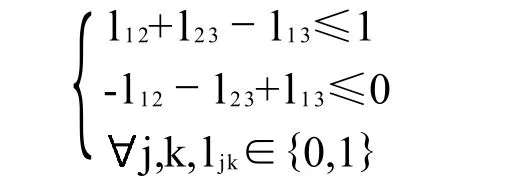
用整数规划法求得最优解为: l12=l13=0,l23=1,社会选择的排序是
实例2参考文献[1]中的例11.7
投票矩阵为:
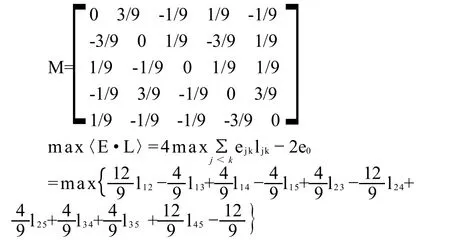
受约束于:
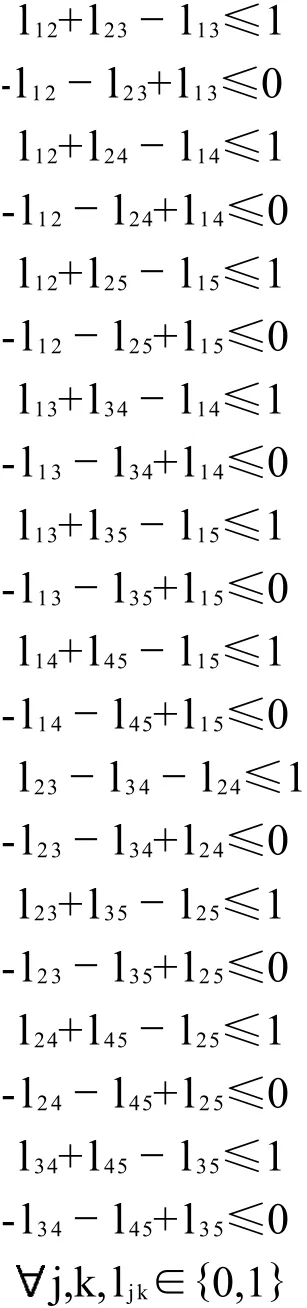
最优解为:l12=l14=l15=l25=l34=l35=l45=1,l13= l23=l24=0,max〈E·L〉社会选择的排序是
[1]岳超源.决策理论与方法[M].北京:科学出版社,2004.
[2]胡运权.运筹学教程[M].北京:清华大学出版社,1998.
[3]徐小湛.Kemeny社会选择函数的一种改进算法[J].西南民族大学学报(自然科学版),2003,29(6):655-659.
0-1 programming algorithm of Kemeny social choice function
WU Xiang-biao
(School of Mathematics and Computation Science,Zunyi Nomal College,Zunyi 563002,China)
Kemeny is a function of a social choice function in group decision making,and this paper will calculate the Kemeny function into solving integer programming model,and proposes an effective algorithm.
Kemeny function;social choice function;group decision making;integer programming
C934
A
1009-3583(2014)01-0081-03
2013-11-05
吴祥标,男,湖北仙桃人,遵义师范学院数学与计算科学学院讲师,硕士。
朱 彬)

