Menelauss定理在解析几何中的应用

邓小华

（四川广播电视大学，四川成都610073）

Menelauss定理在解析几何中的应用

邓小华

（四川广播电视大学，四川成都610073）

Menelauss定理往往应用在平面几何和立体几何中，在解析几何中的应用却很少见。作者介绍了Menelauss定理，并将其应用到解析几何中，使解析几何问题得到大大简化，体现了该定理应用的针对性与广泛性。

解析几何；Menelauss定理;圆锥曲线.

早在公元1世纪，古希腊数学家和天文学家梅涅劳斯（Menelauss）解决了初等几何和近世几何中一个非常重要的问题——共线点问题。他提出了一个应用非常广泛的古典定理——Menelauss定理。但随着希腊奴隶社会的崩溃,欧洲封建宗教的残酷统治使梅涅劳斯定理被世人遗忘了一千多年，直到十七世纪欧洲文艺复兴时期，才被意大利数学家兼水利工程师塞瓦重新发现而流传于世。该定理不仅叙述简单，而且形式优美，曾吸引了不少人的兴趣。

近年来，对Menelauss定理及其变形的证明和应用在竞赛数学中研究非常广泛。赵卫东研究了Menelauss定理的推广及其应用[1]，他将Menelauss定理推广到三角形内线段之比，并举例应用于解有关三角形内线段之比的中学数学竞赛题；湖北省武穴师范的洪凰翔、杨利民分析了四面体中的Menelaus定理；临沂师范学院数学系的焦圣华研究了Menelauss定理在平面几何中的应用，他举例说明了用Menelauss定理来解决平面几何中的有关问题，尤其是在中学数学竞赛中的三点共线、两角相等、直线平行等题目，能使解答简化。

人们对于Menelauss定理的应用往往都在平面几何和立体几何方面，在解析几何中的应用却很少。其实，Menelauss定理也可以应用于解析几何中，运用恰当，在解决问题时可达到事半功倍的效果。

1 准备知识

1.1 Menelauss定理

1.2 Menelauss定理的逆定理

2 Menelauss定理在解析几何中的应用

首先，用Menelauss定理证明解析几何中圆锥曲线的一个优美性质[2]：

定理：P为椭圆外一点，过P任意作两条直线，分别与椭圆相交于A、B和C、D，直线AD、BC和AC、BD分别相交于T、S两点，椭圆的弦AB、CD（及其延长线）与TS分别相交于G、H两点。过P点作直线TS的平行线PMN与直线AD、BC相交于M、N两点，与直线AC、BD相交于M′、N′两点。则：P点与G点、P点与H点分别调和分割椭圆的弦AB、CD，且PM=PN，PM′=PN′。

下面，用Menelauss定理证明此结论。

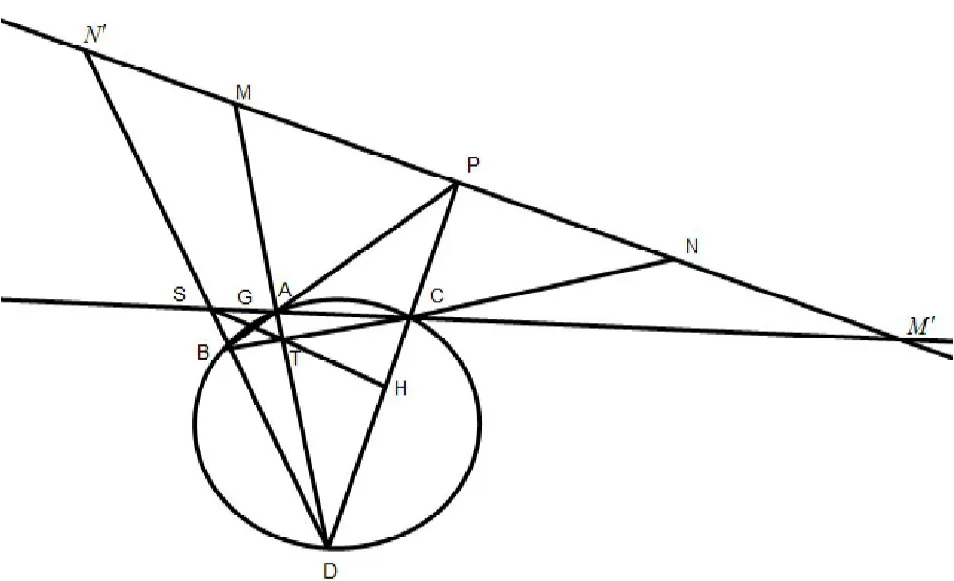
图1

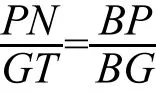
以上结论是P点在椭圆外的情形，同理可以证明P点在椭圆内也有同样的结论。事实上，这个结论可以推广到双曲线和抛物线，用Menelauss定理证明，过程类似。

下面我们研究两个具体的问题：

（1）求椭圆C的方程；

（2）若AB为垂直于x轴的动弦，直线l:x=4与x轴交于点N，直线AF与BN交于点M.

1)求证：点M恒在椭圆C上；

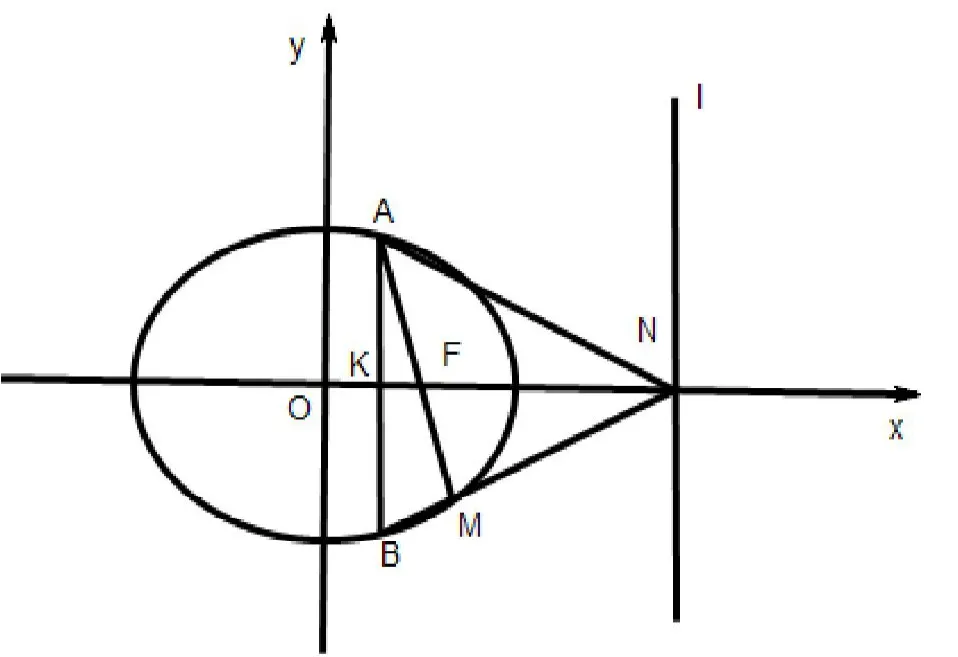
图2

下面我们着重分析第二问：这也是一道十分具有几何特色的圆锥曲线问题，背景是椭圆的几何性质。题目中直线l是椭圆的准线，要证明点M恒在椭圆 C上，只要证明其符合椭圆定义即可。三角形ABM中的三边及其延长线交x轴于点K、F、N，由Menelauss定理

故点M恒在椭圆C上。

运用Menelauss定理解决点恒在曲线上的问题，避开了大量的计算，给解题带来了极大方便。下面再通过一个例子说明定理的妙用。

图3

上述方法是解答本题的常规方法，但计算量大，容易出错。一般地，容易想到的方法，解答的过程和计算量都会很大，而巧解的方法却能大大地减少计算量，节约做题的时间。下面用Menelauss定理解答本题。

又B1、B2关于x轴对称，则

又|HB1|=|HB2|，那么

设B(x1,y1)、B2(x2,y2)到左准线的距离分别为d1= a+ex1、d2=a+ex2，过H作直线l垂直于x轴，垂足H，B、B2到直线l的距离分别为d3、d4，则d1+d2=d3+d4=| x1-x2|,

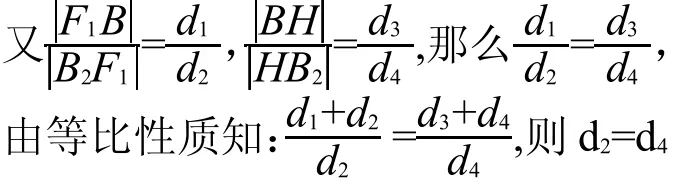
即双曲线的左准线与直线l重合。于是，点H为左准线与x轴的交点。故点H的横坐标

从上面的解法不难看出，应用Menelauss定理解答本题可以避开大量的运算，很容易操作。

3 小结

总之，Menelauss定理不仅在解决有关“点的共线性”时是一个有力的工具，在研究解析几何中的问题时，它也会给我们带来许多方便。由于定理本身的种种优点，运用它并不困难，所以介绍给中学生能给中学生解题带来很大的方便。

[1]洪凰翔,杨利民.四面体中的Menelaus定理[J].中学数学, 1999,(10):21.

[2]姜坤崇.圆锥曲线的一个优美性质[J].中学数学,2005,(10):11.

[3]赵卫东.梅涅劳(Menelaus)定理的推广及其应用[J].咸宁师专学报,2001,(10):58.

[4]焦圣华.梅涅劳斯定理在平面几何中的应用[J].科技资讯科技资讯,2008,(20):40.

[5]仉晋平.梅涅劳斯定理的等价三角形式及其应用[J].中学数学参考,1996,(11):23.

[6]朱家海.梅涅劳斯定理的变形在解竞赛题中的应用[J].中学数学教学参考,1996,(6):35.

Application of Menelauss Theorem in Analytic Geometry

DENG Xiao-hua

(Sichuan Radio and TV University,Chengdu 610073,China)

The Menelauss theorem often occurs in the plane geometry and solid geometry,but it may be seldom applied in analytic geometry.In the paper,the Menelauss theorem was introduced and applied in analytic geometry,which simplify the way to solve the relevant questions in analytic geometry.It is indicated that the Menelauss theorem can be applied specifically and widely.

analytic geometry;Menelauss theorem;conic curve

G633.6

C

1009-3583（2014）01-0084-03

2013-11-13

邓小华，女，四川遂宁人，四川广播电视大学教师，硕士，主要从事数学教学研究。

朱 彬）