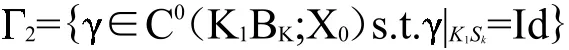半线性分数阶椭圆型算子方程近共振问题的多重解

郭灵钟，姚 娟，索洪敏，张 鹏

（1.贵州民族大学理学院，贵州贵阳550025；2.遵义师范学院数学与计算科学学院，贵州遵义563002）

半线性分数阶椭圆型算子方程近共振问题的多重解

郭灵钟1，姚 娟1，索洪敏1，张 鹏2

（1.贵州民族大学理学院，贵州贵阳550025；2.遵义师范学院数学与计算科学学院，贵州遵义563002）

利用临界点理论中的环绕定理研究分数阶椭圆型算子，得到了半线性分数阶椭圆型算子方程在非主特征值处近共振问题的存在性和多重解结果。

分数阶椭圆型算子；近共振；高阶特征值；解的多重性；环绕定理

本文研究下面半线性分数阶椭圆型算子方程：

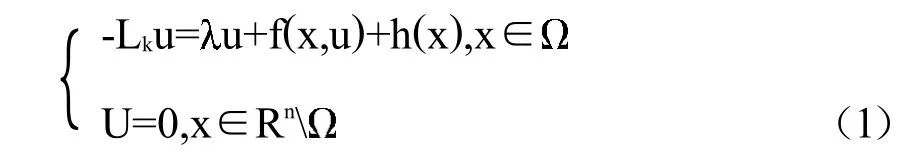
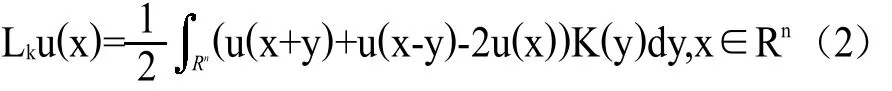
这里的K：Rn{0}→(0,+∞)是一个函数，且满足以下三个条件：

（1）mK∈L1(Rn)，m（x）=min{|x|2，1}；

(f1)对所有一致成立，且对任意的M>0，存在函数，使得对所有的和所有的

特别地，方程（1）的特殊情况如下：

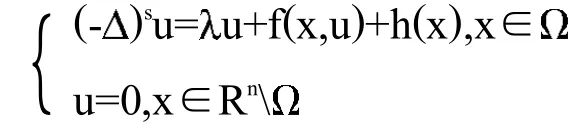
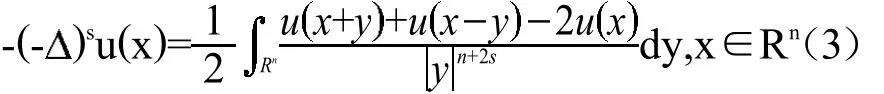
方程（1）对应的半线性椭圆方程

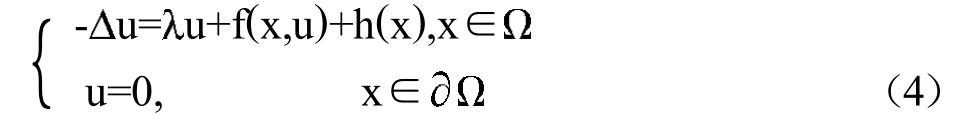
其主特征值的近共振解的存在性与多解性问题,已有很多结果[1-10],这些结果是基于分岐理论和度理论,也有很多结果是基于变分方法.而对于高阶特征值情形,当时有唯一解，当且hkdx=0(k∈Ek)时方程有无穷多解.而当非线性项满足恰当的条件,充分接近k时泛函的几何结构很快改变.所以如果给扰动项f恰当的条件就可以有多解的存在性.FanciscoOdiardePaiva和EugnioMassa在文献[11]中考虑了当f次线性且在无穷远处满足一定的条件时利用环绕定理给出了高阶特征值的近共振问题解的多重性,利用该文的基本思想,本文将相关结果推广到分数阶椭圆型算子方程(1)，得到了f在无穷远处次线性时高阶特征值处的近共振问题解的多重性。

1 有关预备知识及结果

方程[1]的弱解可通过下面方程给出

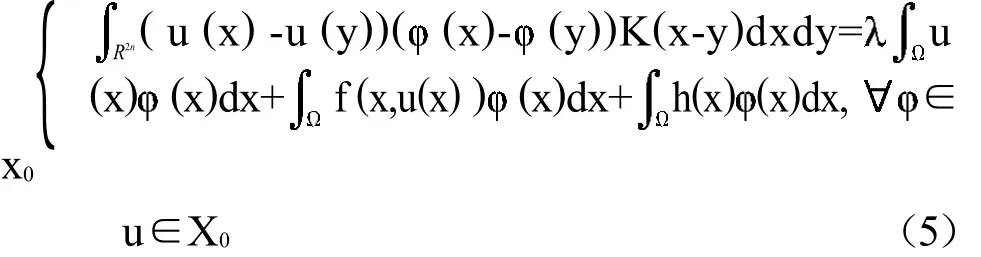
这里，X是一个Rn到R的Lebesgue可测函数空间，X中任意函数属于L2()，且映射 (x,y)(g(x)-g属于

X0={g∈X:g=0,a.e.在Rn中}是一Hilbert空间（详见文献[15]）。其上范数定义为：

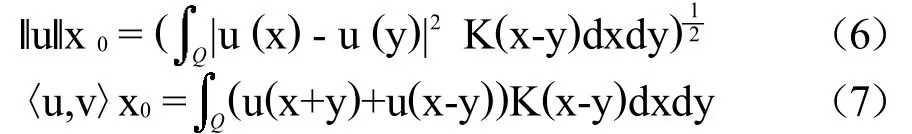
考虑泛函J:X0→R:

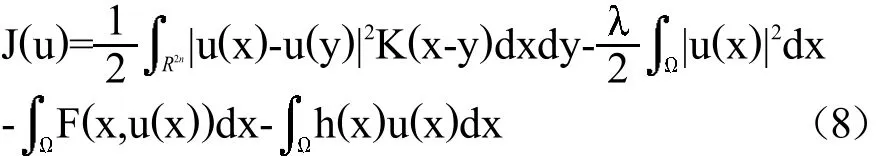
由给定条件知u∈X0是方程(1)的弱解当且仅当u是泛函J的临界点。

定义：Bk-1={u∈Hk-1:ux0≤1},Bk={u∈Hk:ux0≤1},,Sk-1,Sk,分别表示Bk-1,Bk,的球面。

由假设(f1)对任意的>0，存在M>0和gM∈L2，使得：

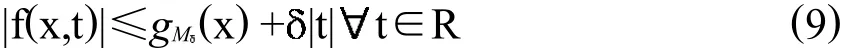
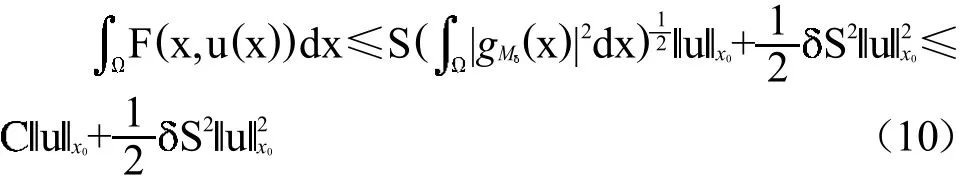
其中S是X0嵌入到L2()的最佳常数

对于特征值空间的分解，通过简单计算就有如下标准不等式：

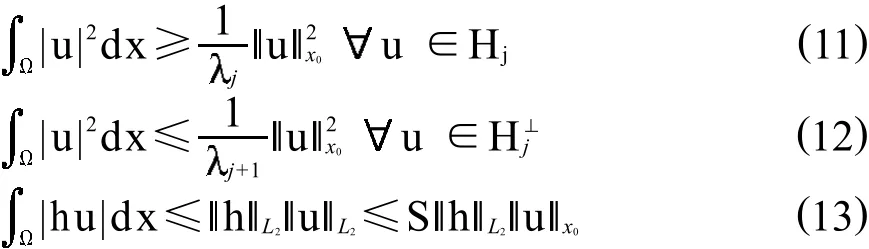
现给出本论文的主要结果：

（H1）（f2）:lim f(x,t)=±∞关于x∈一致成立;

(H2)(f3):limF(x,t)=+∞关于x∈一致成立；

2 定理的证明

定理的证明：先证明泛函J满足PS条件.

设{Un}X0满足{J(Un)}是有界的且{J′(Un)→0, (n→∞),则可证{Un}有界。假设令un=vn+wn∈其中vHk-1,wn∈由(11)和(12)得

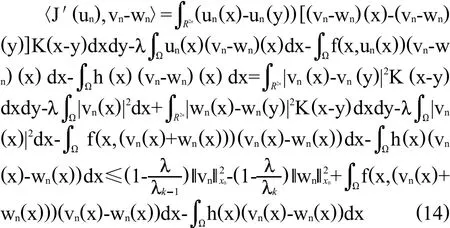
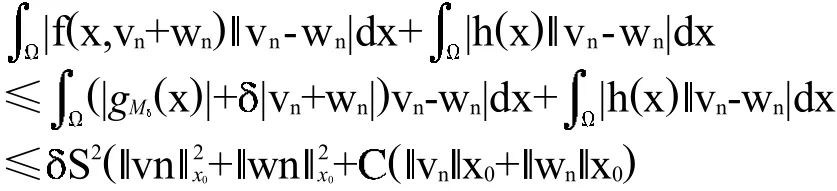
因为J′(un)→0(n→∞),因此存在n>0,使得对所有n>N,有

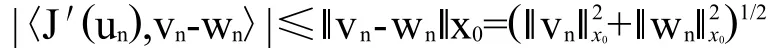
于是对所有n>N,由不等式(14)得到

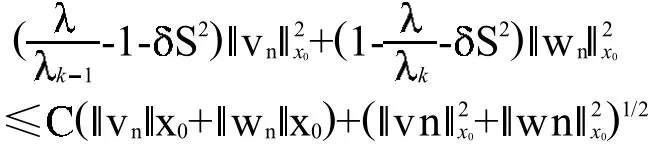
下证un有收敛的子列。

由于un是中的有界子列，X0是自反的（因为X0是一Hilbert空间），所以存在子列，我们仍记为un，有u∞∈X0使得

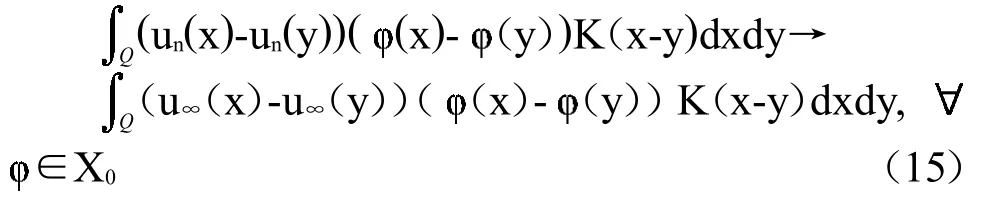
当n→+∞通过文献[15]引理8，有

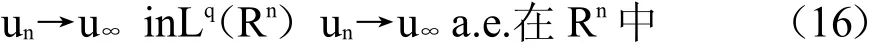
当n→+∞.并且，这里存在∈Lq（Rn）使得

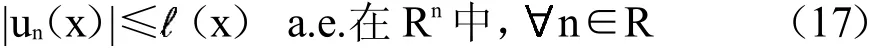
显然映射tf（·,t）是连续的，由控制收敛定理可得

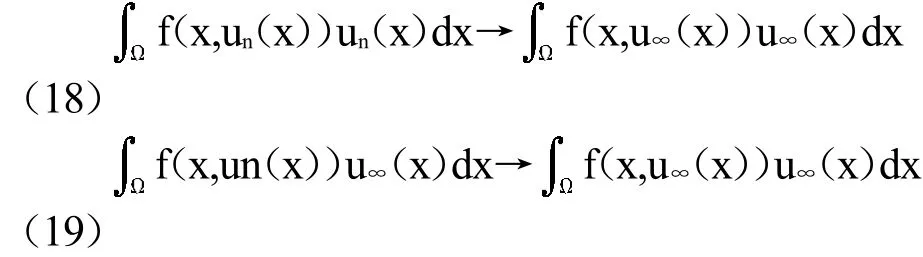
当n→+∞又

由（18）式，我们得

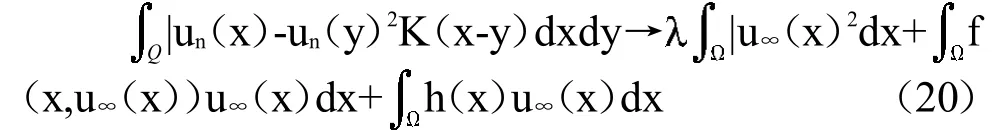
当n→+∞并且,

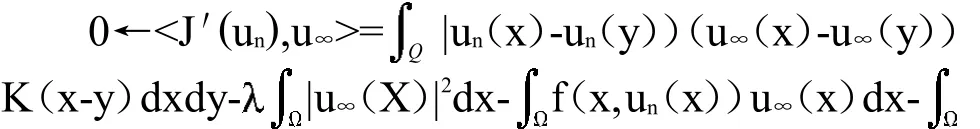
当n→+∞由（15）,（19）和（21）式，得

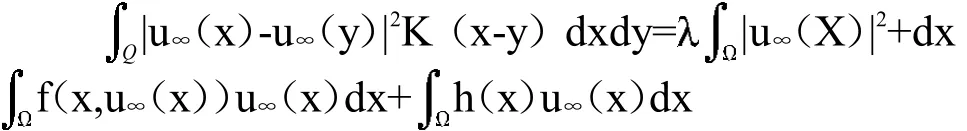
而由（20）和（22）式可得

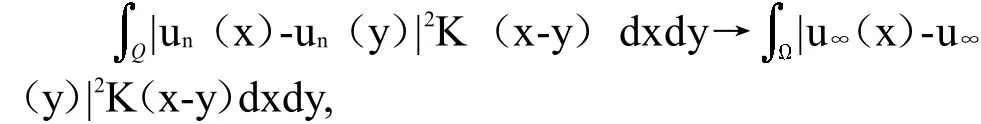
因此

最后，有

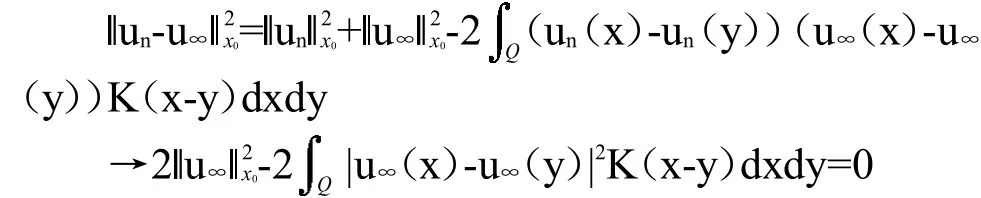
当n→∞综上，un存在收敛的子列，故J满足（PS）条件.

下面利用环绕定理得到方程（1）的第一个解.

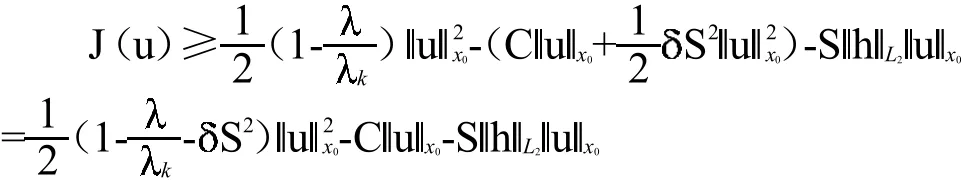
另一方面对u∈HK-1利用（10），（11），（13）得到

所以对任意给定的K（这里取K为下面引理2的K1），能找到充分大的（ >K）使得对任意的

为了得到第二个解，需要下面的引理.

引理1假设（f1）和（f3）成立，则存在一个非减函数D:（0,+∞）→R使得

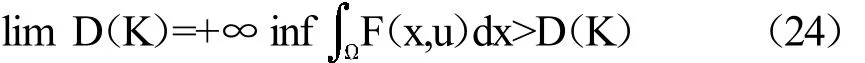
证明:由（f3），存在t0使得对所有|s|>t0，F（x,s）≥M关于所有X∈一致地成立.

由（9），对于|t|≤t0，有

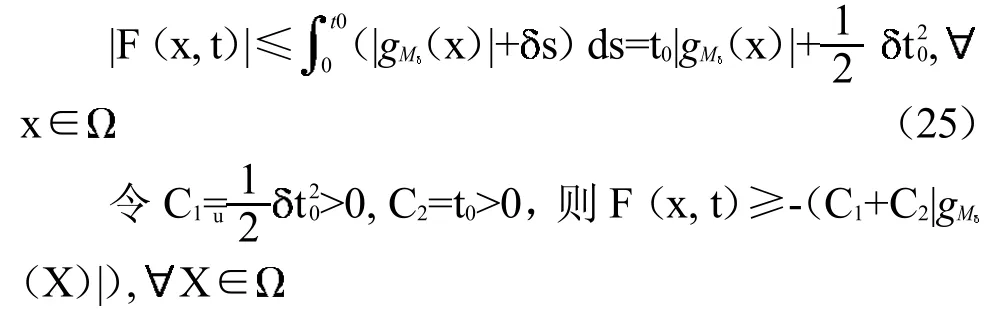
事实上，u∈L∞（详见文献[16]），即|u（x）|≤esssup|u（x）|，X∈其中esssup|u（x）|表示函数u（x）的绝对值的本性上确界.而由（11）有假设这样的不存在，于是对一列存在un∈Sk使得，于是有由un本性有界知道等式右边收敛于0，矛盾.下面取，

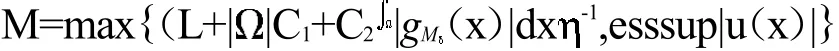
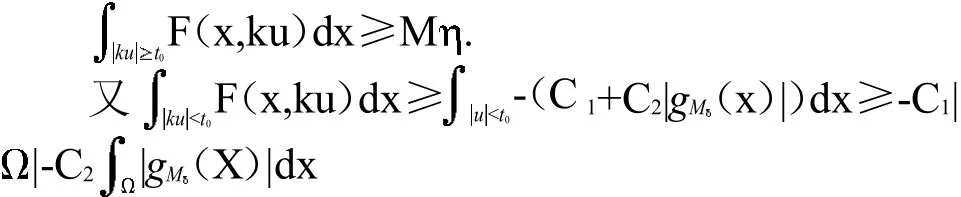
于是得到：

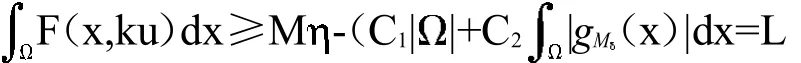
引理2如果（f1）以及假设（H1）和（H2）之一满足，则存在证明：设u∈H┴k:利用（9）,（10）,（12）和（13）得到如下不等式：

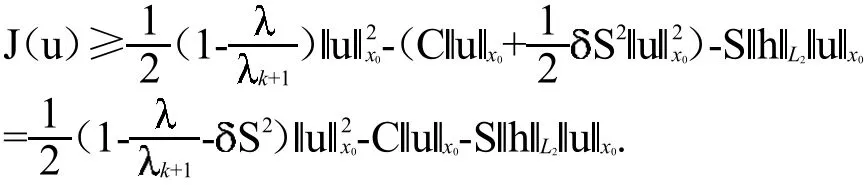
先考虑（H1）和（f1）的情形.通过简单计算可得：对任意给定的M>0，

存在常数C3,C4和gM∈L（2），使得F（x,t）≥M|t|

下面令.M=1+s hL2

设u∈KSHk，在有限维子空间中，所有范数等价，所以令

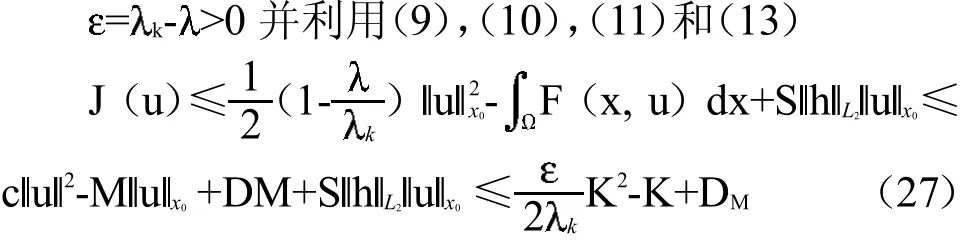
现在考虑（H2）满足情形，设D（K）是引理1中的函数；对 ux0

=K，

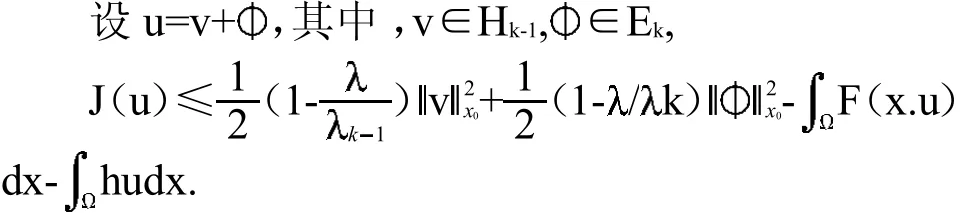
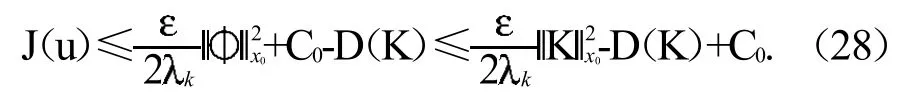
由（24）知lim D（K）=+∞，固定K1使得C0-D（K1）

令

因为K1Sk与环绕，由环绕定理和引理2得到第二个解记为uk,对应的临界值为（v））为了完成定理的证明，需要给出上面的两个解是不同的.

由引理2知道 Ck≥D1，接着构造一个连续映射→X0如下：

其中ek∈Ek且.ekx0=1.

[1]J Mawhin,K Schmitt.Nonlinear eigenvalue problems with the parameter near resonance[J].Ann Polon Math,1990,(51): 241-248.

[2]D Lupo,M Ramos.Some multiplicity results for two-point boundary value problems near resonance[J].Rend Sem.Mat. 1990,48(2):125-135.

[3]T F Ma,M Ramos,L Sanchez.Multiple solutions for a class of nonlinear boundary value problems near resonance:a variational approach.Proceedings of the Second World Congress ofNonlinearAnalysts[J].NonlinearAnal,1997,30(6):3301-3311.

[4]M Ramos,L Sanchez.A variational approach to multiplicity in elliptic problems near resonance[J].Proc Roy Soc Edinburgh,1997,Sect A 127(2):385-394.

[5]J Mawhin,K Schmitt.Landesman-Lazer type problems at an eigenvalue of odd multiplicity[J].Results Math,1988,14(1-2): 138-146.

[6]E Jannelli.The role played by space dimension in elliptic critical problems[J].J Differential Equations,1999,(156): 407-426.

[7]P de Nápoli,M Mariani.Three solutions for quasilinear equations in near resonance.Proceedings of the USA-Chile Workshop on Nonlinear Analysis[M].Vina del Mar-Valparaiso, 2000.131-140.

[8]S Wu,HYang.A class of resonant elliptic problems with sublinear nonlinearity at origin and at infinity[J].Nonlinear Anal, 2001,45(7):925-935.

[9]T F Ma,M L Pelicer.Perturbations near resonance for the

p-Laplacianin RN[J].Abstr Appl Anal,2002,7(6):323-334.

[10]Z-Q Ou,C-L Tang.Existence and multiplicity results for

some elliptic systems at resonance[J].Nonlinear Anal,2009, (71):2660-2666.

[11]F O de Paiva,E Massa.Semilinear eliptic problems near resonance with a nonprincipal eigenvalue[J].J Math Anal Appl, 2008,(342):638-650.

[12]陆文端.微分方程中的变分法(修订版)[M].北京：科学出版社，2003.

[13]Hong-Min Suo,Chun-Lei Tang.Multiplicity results for some elliptic systems near resonance with a Nonprincipal eigenvalue[J].Nonlinear Analysis,2010,(73):1909-1920.

[14]E Di Nezza,G Palatucci,E Valdinoci.Hitchhiker’s guide to thefractionalSobolev spaces[J].BullSciMath,2012,136(5): 521-573.

[15]RServadei,EValdinoci.Mountain passsolutions fornon-local elliptic operators[J].J Math Anal Appl,2012,389(2): 887-898.

[16]Aliang Xia,Jianfu Yang.Regularity of nonlinear equations for fractional Laplacian[J].Proceedings of the American Mathematical Society,2013,S 0002-9939 11734-X.

The multiple Solutions to the Near Resonance Problems of Semi-linear Fractional Order Elliptic Operator Equation

GUO Ling-zhong1,YAO Juan1,SUO Hong-min1,ZHANG Peng2

(1.School of the Science,Guizhou Minzu University,Guiyang 550025,China 2.Department of Mathematies,Zunyi Normal College, Zunyi 563002,China)

The linking theoremin the critical point theory is used to study fractional orderelliptic operator,and we can obtain the existence and multiple solutions about the near resonance problem of the non-principal eigenvalue for the semi-linear fractional order elliptic operator equation.

fractional order elliptic operator;near resonance;high order eigenvalue;multiplicity of solution;linking theorem

O175.25

A

1009-3583（2014）01-0087-05

2013-11-04

贵州省科学技术基金资助项目（黔科合J字[2013]2141号，黔科合J字LKM[2011]31号）；贵州民族大学2013年科研项目

郭灵钟，男，贵州纳雍人，贵州民族大学理学院硕士研究生。研究方向：非线性泛函分析。

朱 彬）