改进的一站固定式双基SAR频域成像方法
金日初 王 宇 邓云凯 邵云峰② 赵 硕②
①(中国科学院电子学研究所 北京 100190)
②(中国科学院大学 北京 100049)
1 引言
双基合成孔径雷达(Bistatic Synthetic Aperture Radar,BiSAR)相比于传统的单基SAR有以下优点:隐蔽性好、抗干扰强、生存能力强;可获得地物非后向散射系数;可以进行前视成像;可提高系统信噪比;利用多个不同基线的双基SAR可进行干涉测量等等[1-3]。一站固定式是一种特殊的双基模式,该模式是将双基中的一个基站固定,而令另一个基站运动。这种模式的双基SAR组建起来比较容易,而且应用灵活,因此有着广泛的应用前景[4]。
一站固定式虽然构造简单,但是因为其特殊的几何构型,其信号具有极强的2维空变性,给成像处理带来了极大的困难[5]。目前,应用最为广泛的是时域BP成像算法[6],该算法可以较好地解决2维空变性问题,但是其运算量巨大,虽然最近提出了一些快速算法[7,8],但是相对于传统的频域算法,仍需要较长的处理时间,所以不适合进行实时成像处理;另一种比较实用的算法是NLCS算法,该算法的提出最初是为了缓解单站 SAR中距离调频率的空变问题,后来被应用到移不变模式的双基成像中[9],并取得了很好的效果,但是该方法在一站固定模式下,无法有效地解决方位向的空变性问题;文献[10]对NLCS算法进行了修改,修改后的算法能较好地解决一站固定式模式下的2维空变性,但是其推导过程比较复杂而且使用了大量的近似,使用范围受到一定的限制。相比以上两种方法,文献[11]提出的基于分块和插值的方法推导过程比较简单,容易理解,而且具有较好的成像效果,但是由于其分块是在插值之前进行,很难保证插值后每块边缘点处的聚焦效果。本文在该方法的基础上,通过计算出双基与场景位置的准确关系,采用类似于 BP的逆向法进行分块,可以有效地解决边缘点的问题;同时提出更为准确的插值关系,消除了由固定端斜距引入的图像几何形变,得到类似单基的斜距图像。
本文主要分成4个部分:首先介绍一站固定模式的几何模型,并推导出双基和目标点位置间的准确关系;接着介绍改进后的算法,包括新的分块方法以及新的插值关系;然后是仿真以及实测数据的处理;最后对该改进算法进行总结得出相关结论。
2 一站固定模式的几何模型
一站固定式双基SAR要求一个基站是运动的,另一个基站是固定不变的。为了叙述简便,本文令发射端运动,而接收端固定不变,其几何模型如图1所示。
在图1中,我们用Y轴表示发射端的运动方向,用Z轴表示高度,lT为发射端的轨道,lR为接收端的等效轨道(因为接收端不运动,所以这个轨道并非真实存在),显然,lT,lR与 Y轴相互平行。目标点在坐标系中的位置为(xp,yp,zp),发射端在坐标系中的位置为(xT,yT,zT),接收端在坐标系中的位置为(xR,yR,zR)。r0T为目标到lT的最近距离,r0R为目标到lR的最近距离。因为r0T垂直于lT,r0R垂直于lR,所以r0T与r0R同时垂直于Y轴,即位于垂直于Y轴的同一平面内。Vr为发射端的等效速度。
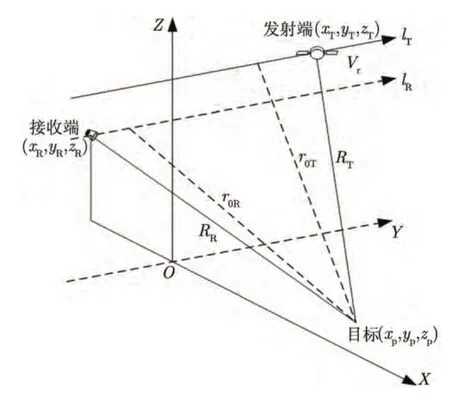
图1 一站固定模式成像几何模型Fig.1 The geometry model in the one-stationary mode
根据图 1所示的几何关系,如果用η表示发射端运动的时间,并令 yT=Vr⋅η,定义η的零点为发射端与接收端相距最近的时刻,即 yT=yR的时刻,ηp为发射端与目标点最近的时刻,即 yT=yp的时刻,这样有 yR=Vr⋅0,yp=Vr⋅ηp,那么目标到发射端的斜距可以表示为:

目标到接收端的斜距可以表示为:

因此,回波信号的总斜距为:

通过式(3),我们发现双基回波信号的斜距历程除了由发射端斜距 RT(η;r0T,ηp) 引入的距离徙动之外,还有由接收端斜距 RR(r0R,ηp) 引入的距离偏移。图2显示了具有相同r0T的不同目标点的斜距历程,其中图 2(a)显示了目标点P1到P5的成像几何模型,图2(b)则显示了这些目标点的信号轨迹。
距离偏移的存在使一站固定模式的回波信号具有2维空变性,这大大增加了成像处理的难度。我们发现距离徙动与r0T有关,而距离偏移与r0R有关,如果能找到r0T和r0R之间的关系,便可以设法将距离徙动和距离偏移统一起来,降低处理的难度。观察图 1,可以发现由于发射端轨道和接收端轨道的位置是相对固定的,因此r0T和r0R之间存在一定的关系,且根据前面的分析,r0T与r0R位于垂直于 Y轴的同一平面内,如图3所示,这样就可以找到r0T和r0R之间的关系。
图3中,HT和HR是发射端和接收端相对于目标的高度,可以表示为:

rgT和rgR是r0T和r0R在 XY 平面上的投影,rΔ=rgT−rgR,这样可以很容易得到r0T和r0R之间的关系为:

通过式(5)可知,如果已知发射端和接收端相对于目标的高度HT和HR以及发射端和接收端在XY平面投影的最近距离rΔ,那么便可以准确地建立r0T和r0R之间的关系,而在实际情况下,这些参数都是很容易获得的。因此式(2),式(3)中与r0R有关的变量RR(r0R,ηp)和R(η;r0T,r0R,ηp)都可以改写成与r0T有关的形式,即 RR(r0T,ηp)和R(η;r0T,ηp)。本文就是利用式(5)所示的关系来进一步完善分块和插值过程的,这一点将在下一节进行仔细描述。

图2 目标点斜距历程示意图Fig.2 Range history of one point target

图3 垂直于Y轴的截面图Fig.3 The image of cross section vertical to axis Y
3 改进的频域成像算法
3.1 频域成像算法的基本流程
针对一站固定式双基信号具有2维空变性的特点,文献[1]提出了一种基于分块和插值的方法。该方法的处理流程如图4所示。
在该算法中,将位于(r0T,ηp)点目标的回波数据表达式记为:


图4 基于分块和插值的频域成像算法流程图Fig.4 The flow chart of the frequency method based on blocks and interpolation
其中τ为距离向时间,η 为方位向时间,σ(r0T,ηp)为目标点的散射系数,Kr为信号的距离向调频率,R(η;r0T,ηp)为式(3)所示的斜距。
通过2维FFT之后,回波信号变换到2维频域,其表达式为:

其中

参考函数H1为:

其中rm为参考斜距,可以取场景中心到发射端的最近斜距。然后将参考函数H1与回波信号的2维频谱相乘,可以得到:

其中,pr(⋅)表示距离向脉冲压缩后得到的包络。此时,完成了一致RCMC以及距离向压缩。
为了消除残余的距离徙动,将距离压缩后的图像沿距离向进行分块,然后在每一小块中选取参考斜距rn,构造参考函数Hn,即:

这时将每一小块经过距离向FFT再变回2维频域,然后与参考函数Hn相乘,可以得到:
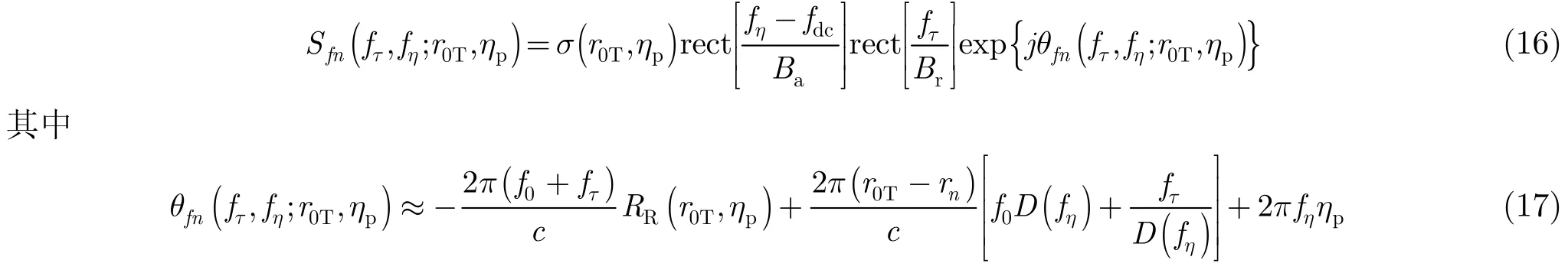
接下来是对每一块进行2维IFFT变换到2维时域。首先,通过距离向IFFT,将信号变换到距离多普勒域,得到的信号可以表示为:

由于 RR(r0T,ηp)引入的距离偏移的存在,同一r0T的目标点分布在不同的距离门上,因此无法在距离多普勒域上直接去除掉方位向残余相位 2π(r0T−rn)f0D(fη)/c 。为了去除这一项,必须首先去除距离偏移,使具有同一r0T的目标点分布在相同的距离门上。我们发现,如果满足:

其中δR表示距离单元的大小,即残余距离徙动的大小不超过半个距离单元的长度,并忽略方位向上的残余相位,那么在方位向上进行IFFT之后的信号可以表示为:

由于分块操作,使方位向残余相位的值大幅度降低,目标点的能量在粗聚焦之后还是大部分集中在了聚焦位置。因此,可以通过插值来完成距离偏移的校正。在文献[1]中,是通过构造以下映射来完成插值操作的:

插值之后信号变为:
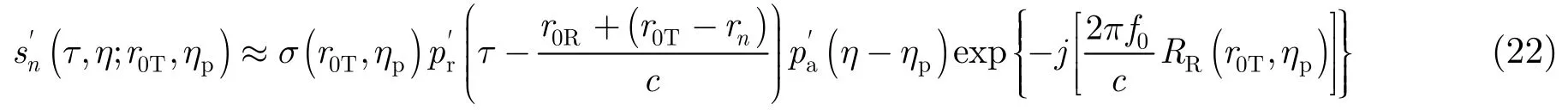
进行方位FFT后,其信号变为:

由于具有同一r0T的目标点具有相同的r0R,因此可以认为具有同一r0T的目标点分布在同一距离门上,因此可以构造参考函数,即:

3.2 改进的频域算法
在 3.1节中叙述的成像算法可以很好地解决一站固定式双基信号中的2维空变性问题,而且步骤简单,易于实现。但是在其处理过程中,并没有考虑r0T和r0R的关系,因此其分块操作以及插值操作处理得并不精细,这会对成像结果产生影响,本文提出的改进算法主要是在这两方面提出了相应的改进。
3.2.1 分块操作的改进 根据图 4所示的处理流程以及3.1节的分析,分块操作是在完成一致RCMC和距离向压缩后进行的。此时,位于(r0T,ηp)的目标点的回波在距离向上被压缩到了

将式(2)代入,可得:

在原方法中,由于不清楚r0T和r0R的关系,所以无法确定Rrd和r0T之间的关系,因此在分块时只能通过一个给定的r0R,然后粗略地找出Rrd和r0T之间的对应关系。由于残存距离徙动的存在,这种粗略的分块很容易漏掉边缘点的部分信息,进而影响到后面的插值操作,最终影响到边缘点的聚焦效果。解决这个问题通常采用的方法是在原有分块大小的基础上增加重叠区域,这样无疑会大幅增加计算量,而且因为Rrd和r0T之间关系的不确定性,在子块拼接时也会出现问题。
在本文中,根据一站固定式双基成像的几何模型,设法找出了r0T和r0R的关系,如式(5)所示,将其代入式(26),便得到了Rrd和r0T之间准确的对应关系,即:

结合式(27)和式(29),可以得到更为精细的分块方法如下所示:
(1) 利用式(29),根据Rrd的分布范围来求出r0T的分布范围;
(2) 根据式(19)确定每块大小,然后在r0T上进行分块,总的块数记为Nblock,其中每一小块标记为k (k=1,2,…,Nblock);
(3) 利用式(27)找出r0T上每一块对应的Rrd的分布范围,完成在Rrd上的分块。
值得注意的是,虽然式(29)是通过近似得到的,但是它仅仅被用于求解r0T整体的分布范围,并不影响分块操作,在分块时采用的是式(27)来寻找子块r0T对应的Rrd,而式(27)是精确的,因此其可以确保在r0T上的子块中的每一个点的信息都包含在Rrd上的子块中。
由于最终要在r0T上进行成像,所以该方法有些类似于BP由图像域的分布反推信号域分布的过程。可以用图5来表示改进后的分块过程。
3.2.2 插值操作的改进 在原方法中,插值是在式(21)所示的映射下进行的,通过该映射关系,原来分布在不同距离门的具有相同r0T的目标点被重新对齐到同一距离门下,从而使方位向上残余相位的校正成为了可能。但是由于不清楚r0T和r0R的关系,在实际操作中,也只能假设一组r0R,然后进行映射。这样做的结果存在两个问题,一是假设的r0R可能与实际情况存在偏差,导致后续的插值以及残余相位补偿不彻底,影响聚焦效果;二是在实际操作中,假设的r0R是均匀采样的,但是由于r0T和r0R之间的关系是非线性的,导致最终的结果 r0R+(r0T−rn)是非均匀采样的,以致最终得到的图像存在畸变。

图5 分块操作示意图Fig.5 The operation of dividing blocks
为了解决这两个问题,利用式(5)所示r0T和r0R的关系,重新构造映射关系为:

式(33)和式(34)反映了新的映射关系下,R0和r0T之间的关系,通过这个关系,可以完成插值操作。由于r0T是根据R0计算出来的,不存在对r0R的假设,因此解决了第1个问题。最终得到的图像是基于r0T轴的,与r0R无关,因此可以通过对r0T进行均匀采样,来得到分布均匀的图像,于是解决了第2个问题。
4 处理结果及分析
为了验证算法的正确性,选择一个3×7的点阵来进行仿真处理。仿真时选用的参数如表1所示。

表1 仿真系统参数表Tab.1 Parameters in simulation
仿真结果如图6所示,其中图6(a)是粗聚焦后的结果,图6(b)是通过插值完成精聚焦后的结果。比较发现,本文提出的新的插值映射关系能够有效地校正接收端斜距引入的距离偏移,而且得到的点阵是均匀排列的,没有出现不均匀采样的现象。
为了更清晰地看到成像效果,对点阵左上角的点进行了点目标分析,其结果如图7和图8所示。
通过点目标分析,可以得到粗聚焦和精聚焦后点目标的峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)如表2所示。

表2 点目标分析结果Tab.2 Point target analysis result
比较图7和图8以及参考表2,可以发现精聚焦之后方位向的聚焦效果有了明显的提升,由此可见本文提出的新分块和插值方法是正确的。
为了比较改进方法相对于原方法在成像质量方面的提升,挑选了某一子块的边缘点,对其成像质量进行分析。其插值后的图像如图9所示。

图6 仿真结果Fig.6 Simulation results

图7 粗聚焦后点目标分析结果示意图(输出为归一化值)Fig.7 Point target analysis after coarse focus (output is normalized)

图8 精聚焦后点目标分析结果示意图(输出为归一化值)Fig.8 Point target analysis after precise focus (output is normalized)
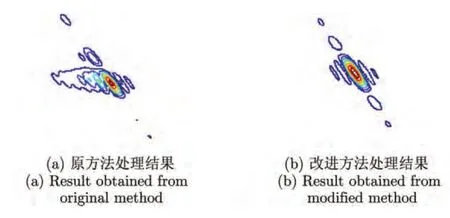
图9 边缘点成像结果示意图Fig.9 Imaging result for one edge point
从图9可以发现,用原方法处理时,点目标插值后的结果出现了明显的扭曲,而采用改进后的方法处理可以得到理想的聚焦效果。因此,改进方法在对边缘点的处理上要优于原方法。
为了进一步验证改进方法的实用性,本文利用该方法对双基实验得到的数据进行了处理,该实验采用TerraSAR-X作为发射端,然后采用固定的接收端去接收回波信号[12]。处理后的图像如图 10所示。

图10 双基实验数据成像结果Fig.10 Imaging result from the bistatic SAR experiment
在图10中,图10(a)为从Google Earth截取的光学图像,图10(b)为利用BP算法成像的结果,图10(c)为采用本文算法的成像结果。比较图 10(b)和图10(c),可以发现本文算法对实测数据的成像效果基本与BP算法一致,但因为本文算法是在频域进行处理,成像时间要明显短于 BP算法,因此本文算法在对实测数据成像方面实用性更强。
5 总结
一站固定式双基 SAR因为其特有的几何构型使其回波具有很强的2维空变性,导致传统的成像算法很难被直接应用。文献[1]提出了一种基于分块和插值的方法,可以很好地解决2维空变性的问题,而且推导过程简单,容易实现。但是在该方法中并没有明确接收端最近斜距和发射端最近斜距之间的关系,因此其分块和插值操作处理得并不精细,导致子块边缘点聚焦效果并不理想,而且由于不均匀采样导致所得图像会存在畸变。本文通过对接收端最近斜距和发射端最近斜距之间关系的准确推导,提出了一种新的分块方法和插值关系。通过仿真及对实测数据进行成像,可以证实,应用本文提出的改进方法,可以很好地解决上述两个问题。
[1]Krieger G and Moreira A.Spaceborne bi- and multistatic SAR: Potential and challenges[J].IEE Proceedings-Radar,Sonar and Navigation,2006,153(3): 184-198.
[2]Massonnet D.Capabilities and limitations of the interferometric cart-wheel[J].IEEE Transactions on Geoscience and Remote Sensing,2002,39(3): 506-520.
[3]Walterschied I,Ender J H G,and Loffeld O.Bistatic image processing for a hybrid SAR experiment between TerraSARX and PAMIR[C].IEEE International Conference on Geoscience and Remote Sensing Symposium,Denver,CO,2006: 1934-1937.
[4]Qiu Xiao-lan,Hu Dong-hui,and Ding Chi-biao.Non-linear chirp scaling algorithm for one-stationary bistatic SAR[C].1st Asian and Pacific Conference on Synthetic Aperture Radar,Huangshan,China,2007: 111-114.
[5]仇晓兰,丁赤飚,胡东辉.双站SAR成像处理技术[M].北京:科学出版社,2010: 148-163.
[6]Mehrdad S.Synthetic Aperture Radar Signal Processing with Matlab Algorithms[M].New York: John Wiley & Sons,INC,1999: 212-214.
[7]Ulander L M H,Hellsten H,and Stenstrom G.Synthetic-Aperture Radar processing using fast factorized backprojection[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(3): 760-776.
[8]Shao Yun-feng,Wang R,Deng Yun-kai,et al..Fast backprojection algorithm for bistatic SAR imaging[J].IEEE Geoscience and Remote Sensing Letters,2012,9(3): 507-511.
[9]Wong F H,Cumming I G,and Neo Y L.Focusing bistatic SAR data using the nonlinear chirp scaling algorithm[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(9): 2493-2505.
[10]Zeng T,Wang R,Li F,et al..A modified nonlinear chirp scaling algorithm for spaceborne/stationary bistatic SAR based on series reversion[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(5): 3108-3118.
[11]Wang R,Loffeld O,Neo Y L,et al..Focusing bistatic SAR data in airborne/stationary configuration[J]. IEEE Transactions on Geoscience and Remote Sensing,2010,48(1):452-465.
[12]Wang R,Deng Y,Zhang Z,et al..Double-channel bistatic SAR system with spaceborne illuminator for 2-D and 3-D SAR remote sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(8): 4496-4507.

