一种自适应迭代的非局部干涉相位滤波方法
林 雪 李曾玺 李芳芳 胡东辉 丁赤飚
①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)
②(中国科学院电子学研究所 北京 100190)
③(中国科学院大学 北京 100190)
④(中国科学技术大学 合肥 230027)
1 引言
干涉 SAR利用两个通道雷达回波的干涉相位信息提取地形高程、运动目标速度、地表形变等各种信息,将SAR的测量拓展到3维空间[1]。在获取相位信息的过程中,干涉相位会受到热噪声去相干、基线或几何去相干、时间去相干等随机误差的影响[2-4],具体表现为相位噪声。低质量的干涉条纹将会影响后续的干涉相位展开及DEM 反演的准确性,最终给高程测量带来误差,影响测绘精度。因此,为获取高质量的干涉相位,必须对干涉条纹进行滤波处理。
针对该问题,前人提出了多种相位滤波方法,这些算法可以分为两类:空域滤波算法,如圆周期均值滤波[5]、圆周期中值滤波[6]、Lee滤波[7]等,以及变换域滤波算法,如Goldstein滤波[8]、小波变换滤波[9]等。其中,变换域滤波算法在实际中应用更为广泛,其基于信号与噪声在变换域中所处的位置不同这一假设来进行噪声抑制,在很多情况下可以得到满意结果。然而,在相干性较差或地形变化剧烈的情况下,由于细节信息与噪声信息在变换域中所处位置无法完全区分,因此上述算法不能同时满足去除噪声和保持相位细节两方面的要求。为得到高质量的干涉相位,有必要研究一种适用于低相干及地形变化剧烈区域的相位滤波方法。
2005年,Buades等人[10]提出了一种非局部平均去噪方法,该方法与以往算法的区别在于其并非基于单个像素点进行处理,而是基于整幅图像或区域,利用了图像的纹理等冗余信息来滤除噪声,从而在滤除噪声的同时更好地保留了图像细节。目前已有许多研究者对该方法进行了改进与拓展,这种非局部去噪的思想在图像/视频处理[11-13]、医学影像[14,15]等多个领域都已得到应用。本文基于上述非局部去噪的思想,提出了一种自适应迭代的非局部干涉相位滤波方法,该方法利用干涉相位概率分布的特点对滤波过程中采用的参数进行自适应,并通过自动迭代完成整个滤波过程。实验表明,该方法在去除噪声和保持相位细节方面都能得到令人满意的结果,在低相干及地形变化剧烈的情况下依然有效。
本文内容安排如下:第1节简单介绍了干涉相位滤波的研究背景及现状;第2节对非局部均值滤波方法的基本原理进行简单阐述;第3节详细介绍了本文提出的自适应迭代的非局部干涉相位滤波算法,给出了该算法的流程框架;第4节通过采用仿真及实测数据对几种现存算法与本文算法进行了对比分析,验证了本文算法的有效性;最后总结全文。
2 非局部均值滤波算法
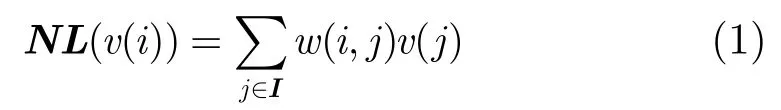
其中w(i,j)表示为恢复像素值v(i)而对像素v(j)赋予的权值,该权值依赖于以像素v(i)和v(j)为中心的邻域像素块Ni与Nj的相似性,且满足条件w(i,j)∈[0,1]以及 ∑j∈Iw(i,j)=1。算法利用两像素块之间的欧氏距离来计算权值函数,即
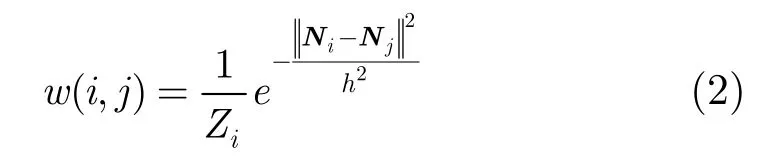
3 非局部干涉相位滤波算法
针对干涉相位自身的特性,本文提出了一种自适应迭代的非局部干涉相位滤波方法。本节首先对权值计算中衰减参数的自适应选择进行说明,之后描述了非局部算法的自动迭代过程,在迭代过程中,调节搜索窗口和邻域窗口使得结果更为精确,接下来给出了自适应迭代的非局部干涉相位滤波算法的整体流程,最后对算法的快速实现进行了简单表述。
3.1 自适应衰减参数选择
衰减参数的选择直接影响权值函数的取值,该参数越大,滤波平滑效果越明显。对于2维灰度图像的经典衰减参数取值为10σn[10],其中σn表示噪声标准差,但该取值在许多情况下并非最优解。研究表明,衰减参数的大小不仅取决于噪声方差大小,且与邻域窗口大小有关[13,16]。因此,可以将衰减参数用噪声方差和邻域窗口大小进行表示。

根据干涉相位的概率密度分布函数[18,19],可以得到干涉相位的噪声方差如式(4)所示,其中Li2(⋅)表示欧拉以2为底的对数,pdf(⋅)表示概率密度分布函数。多视情况下,该表达式的值可以通过数值方法求解获得。
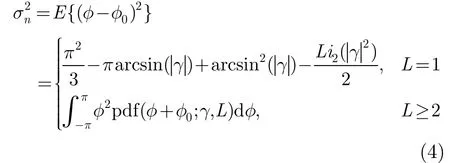
为了尽快促进统计人员熟悉和掌握业务知识,他制定统计管理制度,对统计人员定期进行考核,帮助他们熟悉统计业务,不让他们走弯路。
为得到最优衰减参数的表达式,我们对不同条件下的干涉相位进行了一系列实验。图1(a),图1(b)给出了不同相干系数和邻域窗口条件下,理想相位与滤波相位之间的均方误差(MSE)随衰减参数h变化的曲线,其中,右上角标注的数字表示邻域窗口大小N。这两幅图证明了最优衰减参数值与邻域窗口大小及相干系数有关,且衰减参数值在最优值附近一个较宽的范围内得到的滤波结果变化不大,即具有一定的鲁棒性,为后面的表达式近似提供了条件。图 1(c)给出了最优衰减参数值随邻域窗口大小变化的曲线,其中,左上角标注的数字表示搜索窗口大小,实线对应相干系数为 0.5时的情况,虚线对应相干系数为0.9时的情况。由图1(c)可以看出,最优衰减参数值与邻域窗口大小近似呈线性,拟合得到的线性函数其斜率变化不大,常数项主要受噪声水平影响,搜索窗口对其也有一定影响。图1(d)给出了最优衰减参数值随噪声标准差变化的曲线,其中左上角标注的数字表示邻域窗口大小,实线表示搜索窗口取15×15时的情况,虚线表示搜索窗口取19×19时的情况。由图1(d)可以看出,对于固定的邻域窗口,最优衰减参数值与噪声标准差也近似呈线性,拟合得到的线性函数其斜率基本不变,常数项主要与邻域窗口有关,也受搜索窗口一定影响。根据上述结果,认为最优衰减函数是噪声水平及邻域窗口的线性函数,通过多项式拟合,最优衰减参数可以表示为:
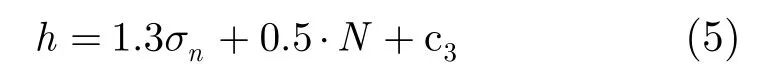
其中c3为常数项,其随干涉条纹疏密程度有所变化。实验得到,在条纹较稀疏的情况下,衰减参数值在相当大的范围内得到的滤波结果变化不大,因此可以简单取值为经典值10σn,而当条纹较密集时,c3取值在−0.5到−1 时通常能得到令人满意的结果。
3.2 自动迭代的非局部滤波算法
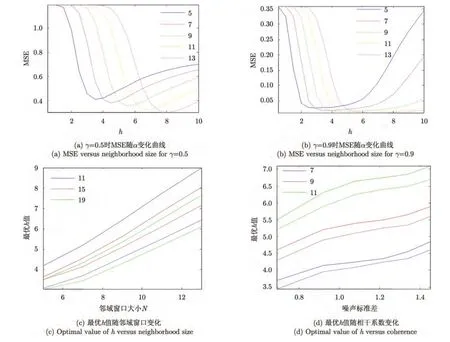
图1 衰减参数曲线Fig.1 Curves of smoothing parameter
搜索窗口与邻域窗口大小的选择直接影响到滤波结果[10,20],其中,搜索窗口对滤波结果的影响尤为明显,图2给出了理想相位与滤波相位之间的均方误差及滤波后干涉相位的残差点数随搜索窗口变化的曲线。可以看出,搜索窗口对滤波结果的影响较大,且滤波结果随搜索窗口尺寸的增大呈现先变好后变差的趋势,这是由于搜索窗口的增大在增加相似纹理区域的同时也增加了所引入的不相似像素块。邻域窗口对滤波结果也有所影响,较小的邻域窗口对高频噪声滤除效果较好,而较大的邻域窗口对低频噪声有良好的滤除作用[21-23]。
文献[24,25]表明,迭代非局部滤波得到的滤波结果较非迭代滤波而言,噪声得到了更好的去除,且图像质量也更为优秀。每次迭代都降低了噪声方差,从而使得权值估计更为准确,最终表现为去噪效果的改善。从最优化角度讲,非局部均值滤波相当于采用Jacobi最优化算法估计理想图像的第1次迭代结果,而多次迭代会进一步降低代价函数,从而达到更好的滤波效果[26]。因此,对干涉相位进行迭代滤波是获取精确相位的有效手段。
由于本文针对的是相干性较差、地形较为复杂区域的干涉相位,因此迭代初始应选择较小的搜索窗口,从而避免引入过多的不相似像素块而影响滤波效果。随着迭代次数的增加,相位噪声逐渐减小,此时逐步增大搜索窗口可以更好地利用纹理冗余信息,从而得到更为准确的滤波结果。而对于每一次搜索窗口大小的取值,不同邻域窗口大小对滤波结果也有所影响,因此,对每一搜索窗口大小的取值,将不同邻域窗口大小得到的结果进行对比,选取最优结果进入下一次迭代,由此实现了搜索窗口和邻域窗口的综合最佳选择。对于仿真干涉相位,可以采用均方误差来评判滤波相位与理想相位之间的差异,而对于实际干涉相位数据,由于无法获取理想相位信息,因此采用残差点数作为衡量滤波结果优劣的指标,由图2可以看出,残差点数的评价效果与均方误差基本是一致的。
为实现算法的自动迭代,采用以下方案进行计算,其中,搜索窗口表示为(2S+1)×(2S+1),邻域窗口表示为(2N+1)×(2N+1)。由于搜索窗口对滤波结果影响相对较大,因此每次迭代的增长步长设为1,邻域窗口对滤波结果影响相对较小,因此步长可较搜索窗口略大,设为2。
步骤1 初始化,分别令(S,N) = (1,1),(1,2),(1,3),对数据进行滤波处理,选出最优结果;
步骤3 S=S0 ≥ 3时,对上一次迭代得到的最优结果分别计算(S,N)=(S0,n),(S0,n+2),(S0,n+4)时的滤波结果,确定本次最优结果对应的参数 N,设为N0;
步骤4 若 N 0 ≠n+4,本次迭代结束,转到步骤5。若N0=n+4,则继续考察N>N0时的滤波结果以获取最佳邻域窗口值,具体操作为:计算(S0,n+k)(k>4且为偶数)时的滤波结果,更新 N0值,直至满足N0≠n+k(即最优结果对应的邻域窗口大小不是目前的最大值)或者N=n+k,n+(k−2),n+(k−4)时的残差点数目不变(即随邻域窗口增大,滤波效果基本不变)这两者中的任一条件时,本次迭代结束,转到步骤5;
步骤5 判断是否继续迭代。具体操作为:若4≤S<10且前后两次迭代的最小残差点数目RES1,RES2满足:(RES1−RES2)/RES1<C,其中,C为常数,且0 <C <0.5(本文实验中取 0.2),即满足前后两次迭代的滤波效果差别不大时,停止迭代;或当S≥10时,停止迭代;否则,S0= S0+1,n=N0,转到步骤3。
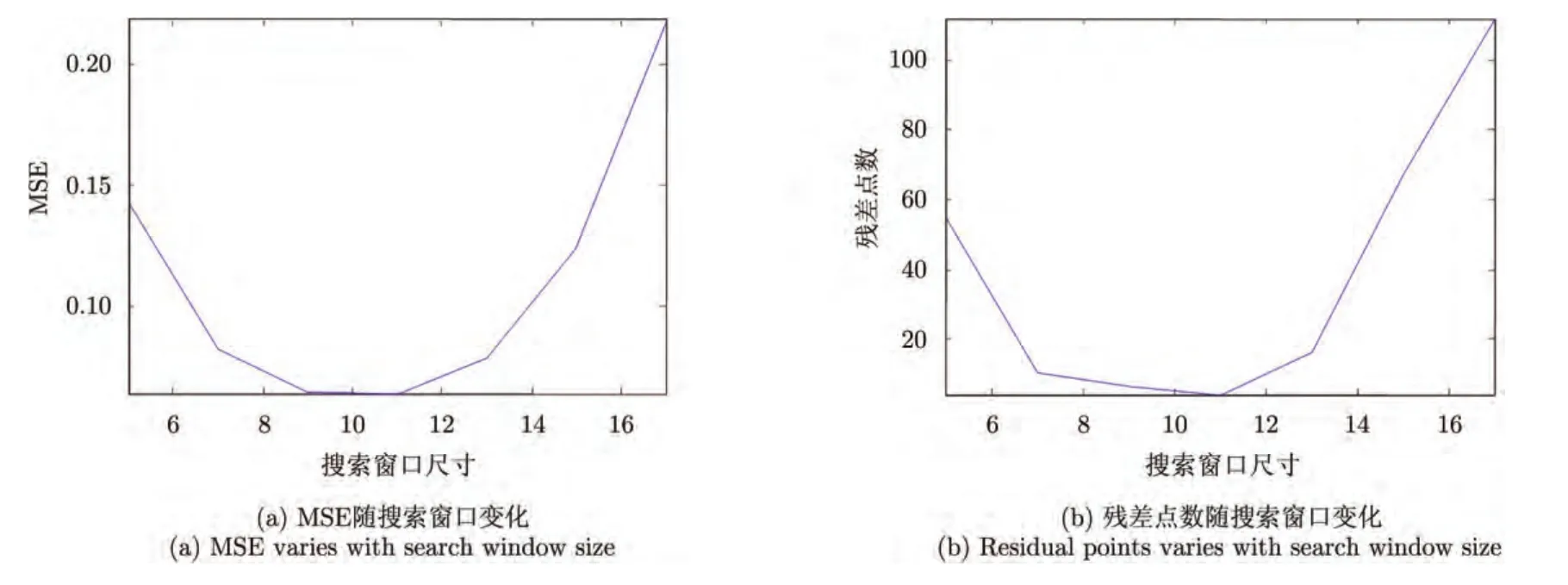
图2 滤波结果随搜索窗口尺寸变化曲线Fig.2 Curves of filtering results versus search window size
3.3 迭代的非局部干涉相位滤波算法
干涉相位的取值范围在(−π,π)之间,并由于相位缠绕存在−π 到π的跳变,直接采用非局部均值滤波算法对干涉相位进行滤波会出现边缘模糊问题(如图3(a)所示)[27,28]。干涉相位在复数域可表示为ejφ=cosφ+j sinφ,其实部Re{ejφ}=cos φ和虚部Im{ejφ}=sinφ 在整个空间内一般是连续的,因此,我们通过对干涉复图像的实虚部分别进行滤波[9],来避免跳变所带来的问题,之后将滤波得到的实虚部合并,最终得到滤波后的干涉相位如图3(b)所示。
综合前文内容,图4给出了本文所提出的迭代非局部干涉相位滤波方法的整体流程框架。其中,为提高算法效率,在计算权值时使用了快速实现的方法,具体方法在下一小节中单独给出。
3.4 算法的快速实现
非局部均值滤波算法的一大问题在于其计算效率低下,针对该问题,目前已有多种提高计算效率的方法被提出[14,17,22,29-33]。本文采用了文献[34]提出的快速计算方法,其利用SSI (Summed Square Image)和FFT实现欧氏距离的快速计算,将计算量由O(M2S2N2)降低到了 O(M2S2)。此外,根据欧式距离的对称性,可进一步降低计算量[31]。同时,对于干涉复图像的实虚部及各次迭代中不同邻域窗口大小的计算可以通过并行处理得以实现,从而使得计算速度进一步提高。
相对于地形变化而言,通常SAR图像具有较高的分辨率,因此进行一定程度的降采样之后仍然可以保持相位纹理。已知非局部算法的计算量与图像尺寸有关,针对结构纹理大于分辨率的干涉相位,本文提出了一种基于降采样的快速实现算法。其具体实现步骤为:
(1) 对原始图像进行n倍降采样,得到n2幅低分辨率的子图像;
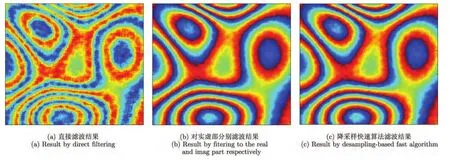
图3 干涉相位滤波结果Fig.3 Interferometric phase filtering results
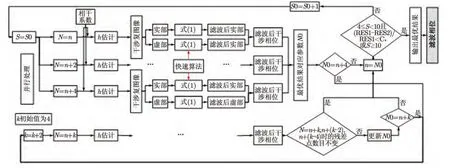
图4 算法流程图Fig.4 Algorithm scheme
(2) 分别对各子图像进行滤波处理,所采用的搜索窗口及邻域窗口大小相应变为原来的1/n;
(3) 对各滤波结果插值使其尺寸达到原始图像大小,此时每点处有n2个滤波结果;
(4) 对这些滤波结果取平均,从而得到该点的最终滤波值。
该基于降采样的快速实现方法使计算量降低为原始算法的1/n4,一定程度上提高了计算速度,且由该算法得到的滤波结果与未采用降采样而得到的滤波结果基本一致(如图3(b),图3(c)所示)。
对于一幅大小为512×512的相位图像,搜索和邻域窗口分别取17×17以及7×7时,采用MATLAB程序处理,原始非局部均值滤波算法时间为1769.30 s,采用基于降采样的快速实现方法,且降采样倍数设为2时,运行时间为467.85 s,速度提高了3.78倍,与理论值有所差距的原因可能在于 MATLAB在矩阵点乘运算中所需时间与计算量不是线性关系;综合采用上述几种快速实现方法,且降采样倍数设为2时,快速实现运行时间为10.47 s,速度提高了约169倍。
4 实验与分析
4.1 仿真数据分析
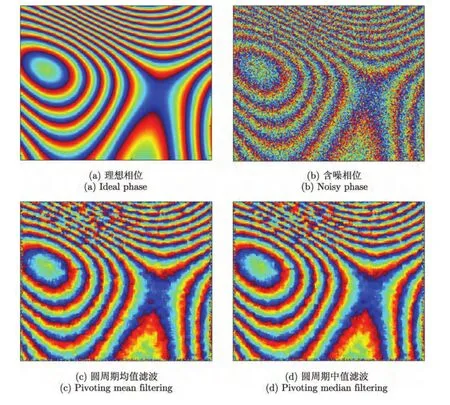
本小节通过对比已有算法与本文算法对仿真干涉相位的滤波效果,验证了本文所提出滤波算法的有效性。根据干涉相位概率密度函数[18,19]仿真生成的理想和含噪干涉相位分别如图5(a),图5(b)所示,本次仿真中,视数L取值为1,相干系数取值为0.5,场景大小为 256×256,条纹密集处每个相位周期变化仅有几个像素。
图5(c)~图5(g)分别表示采用圆周期均值滤波、圆周期中值滤波、Goldstein滤波、Brana滤波、离散小波变换(DWT)滤波所得到的滤波结果,其中圆周期均值、中值滤波采用窗口为7×7,Goldstein滤波及Brana滤波分块为32×32,离散小波变换滤波所采用小波分解层级为 2。表 1给出了采用不同滤波算法滤波前后干涉相位的残差点数及与理想干涉相位之间的均方误差。结合滤波结果和表1中的参数指标可知,上述滤波方法不能很好地平衡滤除噪声和保持相位细节信息二者之间的关系。图5(h)给出了采用本文提出的滤波算法所得到的滤波相位。从直观上看,在所有滤波结果中,其与理想相位最为接近,从表1给出的评价指标看,其残差点数表明噪声得到了很好的滤除,且均方误差很小,表明其与理想相位非常接近,很好地保持了相位细节。综上所述,本文算法在滤除噪声和保持相位细节方面都得到了令人满意的结果。
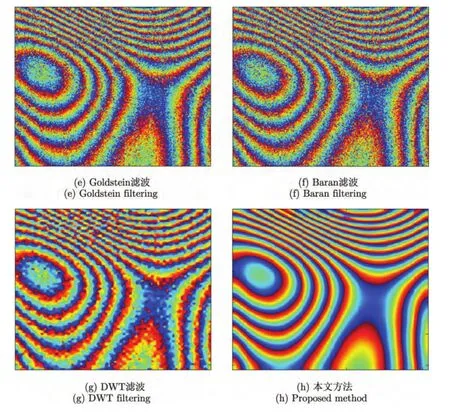
图5 仿真相位及滤波结果Fig.5 Filtered results of simulated data

表1 不同滤波方法效果比较Tab.1 Performance comparison of different methods
运算效率方面,本文算法在3.2节所示的步骤4中消耗时间较多,虽然可通过增大迭代时的增长步长及步骤3中N的取值予以改善,但总体效率较其他算法而言仍相对较低,有待进一步改进。考虑到本文算法主要应用于相干性差、地形变化剧烈的局部区域,该类区域场景大小一般不会很大,另外,即便需处理较大的场景,也可利用分块并行进行处理,因此目前本文算法的运算效率是可以接受的。
4.2 实测数据分析
本小节通过实测干涉相位验证本文所提出的滤波算法的有效性。实验中采用的干涉相位来源于意大利Etna火山(如图6(a)所示),条纹密集处同样只有几个像素,其相干系数如图6(b)所示。图6(c)~图6(h)分别给出了采用圆周期均值滤波、圆周期中值滤波、Goldstein滤波、Brana滤波、离散小波变换滤波以及本文滤波算法所得到的滤波结果,各算法参数设置与4.1节相同。表2给出了滤波前后干涉相位的残差点数及相位标准偏差值(PSD)。从上述结果可以看出,其他算法或者不能很好地滤除噪声,或者在条纹密集处出现交叠等现象,破坏了相位细节,而本文算法在良好地滤除噪声同时,也很好地保持了条纹细节,由此证明了本文算法的有效性。
5 结束语
本文基于非局部去噪的思想,根据干涉相位的自身特性,提出了一种自适应迭代的非局部干涉相位滤波方法。该方法首先利用干涉相位概率分布函数对权值计算中的衰减系数进行估计,实现了衰减系数的自适应,之后通过调节窗口尺寸及自动迭代,最终获取滤波相位。通过仿真与实测数据验证了本文算法的有效性,与目前已有滤波算法对比,其在去除噪声和保持相位细节方面都能得到令人满意的结果。
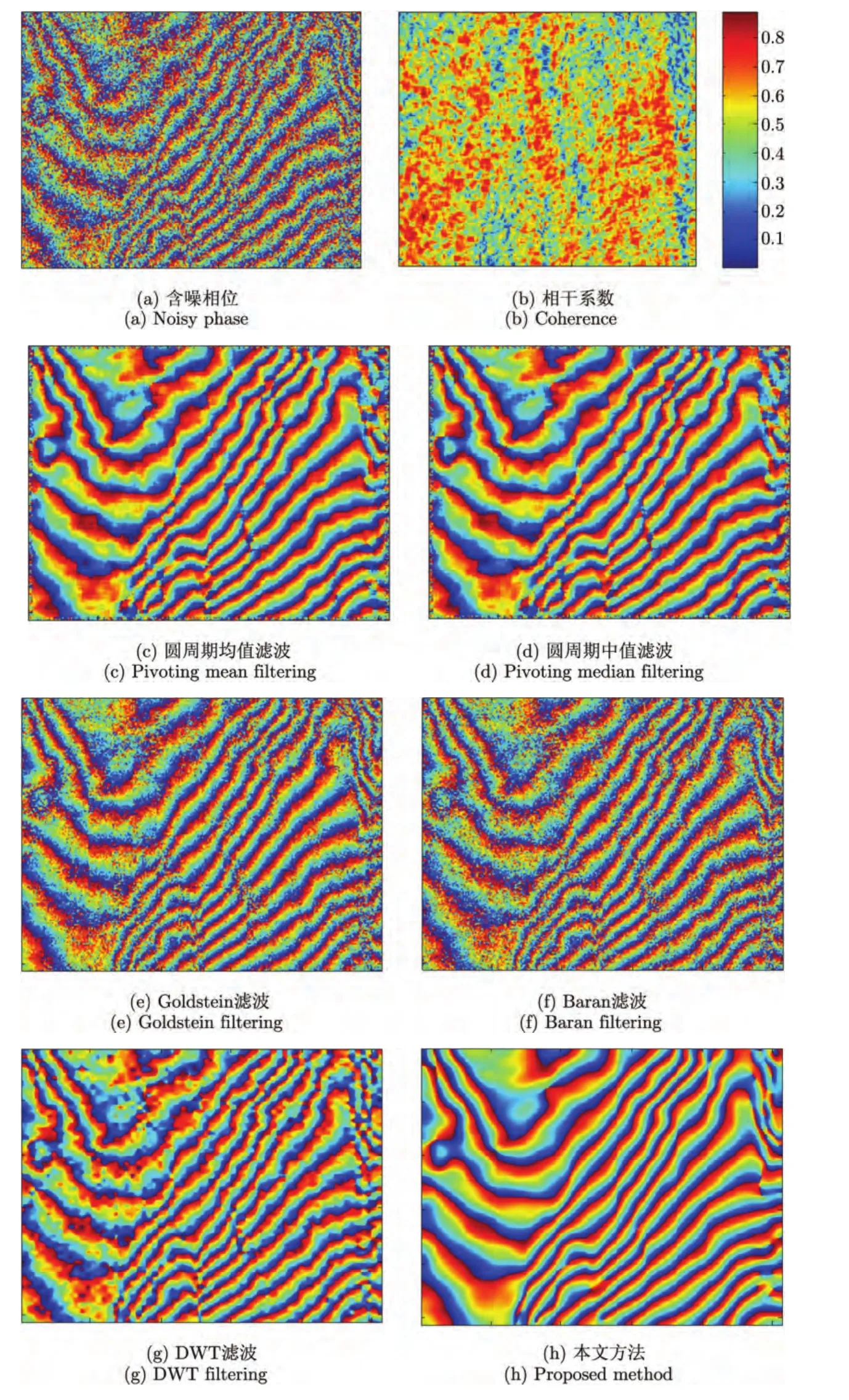
图6 实际干涉相位及滤波结果Fig.6 Filtered results of real data

表2 不同滤波方法效果比较Tab.2 Performance comparison of different methods
[1]Rosen P A,Hensley S,Joughin I R,et al..Synthetic aperture radar interferometry[J].Proceedings of the IEEE,2000,88(3):333-382.
[2]王超,张红,刘智.星载合成孔径雷达干涉测量[M].北京: 科学出版社,2002: 2-17.Wang C,Zhang H,and Liu Z.Spaceborne Synthetic Aperture Radar Interferometry[M].Beijing: Science Press,2002: 2-17.
[3]丁斌,向茂生,梁兴东.射频干扰对机载 P波段重复轨道InSAR系统的影响分析[J].雷达学报,2012,1(1): 82-90.Ding Bin,Xiang Mao-sheng,and Liang Xing-dong.Analysis of the effect of radio frequency interference on repeat track airborne InSAR system[J].Journal of Radars,2012,1(1):82-90.
[4]李焱磊,梁兴东,丁赤飚.机载差分干涉 SAR 双轨法和三轨法的误差比较分析[J].雷达学报,2013,2(3): 326-333.Li Yan-lei,Liang Xing-dong,and Ding Chi-biao.Error comparison and analysis of the two-pass and three-pass approaches in airborne D-InSAR[J].Journal of Radars,2013,2(3): 326-333.
[5]Eichel P H,Ghiglia D C,Jakowatz C V Jr.,et al..Spotlight SAR interferometry for terrain elevation mapping and interferometric change detection[R].Sandia National Labs Tech Report,Washingdon DC,1993,US-DOE.
[6]Lanari R,Fornaro G,Riccio D,et al..Generation of digital elevation models by using SIR-C/X-SAR multifrequency two-pass interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing,1996,34(5): 1097-1114.
[7]Lee J S,Papathanassiou P,Ainsworth T L,et al..A new technique for noise filtering of SAR interferometric phase images[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(5): 1456-1465.
[8]Goldstein R M and Werner C L.Radar interferogram filtering for geophysical applications[J]. Geophysical Research Letter,1998,25(21): 4035-4038.
[9]Martinez C L and Fabregas X.Modeling and reduction of SAR interferometric phase noise in the wavelet domain[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(12): 2553-2566.
[10]Buades A,Coll B,and Morel J M.A review of image denoising algorithms,with a new one[J].Multiscale Modeling& Simulation,2005,4(2): 490-530.
[11]Dabov K,Foi A,Katkovnik V,et al..Image denoising by sparse 3-D transform-domain collaborative filtering[J].IEEE Transactions on Image Processing,2007,16(8): 2080-2095.
[12]Maggioni M,Boracchi G,Foi A,et al..Video denoising,deblocking and enhancement through separable 4-D nonlocal spatiotemporal transforms[J].IEEE Transactions on Image Processing,2012,21(9): 3952-3966.
[13]Tasdizen T.Principal neighborhood dictionaries for nonlocal means image denoising[J].IEEE Transactions on Image Processing,2009,18(12): 2649-2660.
[14]Coupé P,Yger P,Barillot C,et al..Fast nonlocal means denosing for 3D MR images[C].International Conference on Medical Image Computing and Computer-Assisted Intervention,Berlin,Germany,2006: 33-40.
[15]Boulanger J,Kervrann C,Bouthemy P,et al..Patch-based nonlocal functional for denoising fluorescence microscopy image sequences[J].IEEE Transactions on Medical Imaging,2010,29(2): 442-454.
[16]Buades A,Coll B,and Morel J M.Nonlocal image and movie denoising[J].International Journal of Computer Vision,2008,76(2): 123-139.
[17]Coupé P,Yger P,Prima S,et al..An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonane images[J].IEEE Transactions on Medical Imaging,2008,27(4): 425-441.
[18]Lee J S,Hoppel K W,Mango S A,et al..Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing,1994,32(5): 1017-1028.
[19]Tough R J,Blacknell D,and Quegan S.A statistical description of polarimetric and interferometric synthetic aperture radar data[J].The Royal Society A: Mathematical,Physical and Engineering Sciences,1995,449(1937):567-589.
[20]Kervrann C and Boulanger J.Optimal spatial adaptation for patch-based image denoising[J].IEEE Transactions on Image Processing,2006,15(10): 2866-2878.
[21]Lukin A.A multiresoulution approach for improving quality of image denoising algorithms[C].IEEE International Conference on Acoustics,Speech and Signal Processing,Toulouse,France,2006,2: II.
[22]Liu Y L,Wang J,Chen X,et al..A robust and fast non-local means algorithm for image denoising[J].Journal of Computer Science and Technology,2008,23(2): 270-279.
[23]Karnati V,Uliyar M,and Dey S.Fast non-local algorithm for image denoising[C].16th IEEE International Conference on Image Processing,Cairo,Egypt,2009: 3873-3876.
[24]Brox T and Cremers D.Iterated nonlocal means for texture restoration[C].First International Conference on Scale Space and Variational Methods in Computer Vision,Ischia,Italy,2007: 13-24.
[25]Brox T,Kleinschmidt O,and Cremers D.Efficient nonlocal means for denoising of textural patterns[J].IEEE Transactions on Image Processing,2008,17(7): 1083-1092.
[26]Goossens B,Luong H,Pizurica A,et al..An improved non-local denoising algorithm[C].International Workshop on Local and Non-Local Approximation in Image Processing(LNLA),2008: 143-156.
[27]Tahmouresi A A,Saryazdi S,and Seydnejad S R.Non-local means denoising using an adaptive kernel[C].20th Iranian Conference on Electrical Engineering (ICEE2012),Tehran,Iran,2012: 1436-1441.
[28]Salmon J and YannStrozecki.Patch reprojections for Non-Local methods[J].Signal Processing,2012,92(2):477-489.
[29]Dore V and Cheriet M.Robust NL-means filter with optimal pixel-wise smoothing parameter for statistical image denoising[J].IEEE Transactions on Signal Processing,2009,57(5): 1703-1716.
[30]Mahmoudi M and Sapiro G.Fast image and video denoisingvia nonlocal means of similar neighborhoods[J].IEEE Signal Processing Letters,2005,12(12): 839-842.
[31]Dauwe A,Goossens B,Luong H,et al..A fast non-local image denoising algorithm[C].SPIE Electron.Image Processing:Algorithms and Systems VI,San Jose,CA,2008:681210-681210-8.
[32]Orchard J,Ebrahimi M,and Wong A.Efficient nonlocalmeans denoising using the SVD[C].IEEE International Conference on Image Processing (ICIP),San Diego,CA,2008:1732-1735.
[33]Vignesh R,Oh B T,and Kuo C C J.Fast non-local means(NLM) computation with probabilistic early termination[J].IEEE Signal Processing Letters,2010,17(3): 277-280.
[34]Wang J,Guo Y W,Ying Y T,et al..Fast non-local algorithm for image denoising[C].IEEE International Conference on Image Processing (ICIP),Atlanta,GA,2006: 1429-1432.

