利用发射角度的双基地MIMO雷达杂波抑制方法
李 军 党 博 刘长赞 廖桂生
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
双基地雷达发射机可以置于敌方不易攻击的地方,接收机搭载在无人机上靠近感兴趣区域隐蔽侦查。这种配置使雷达具有较好的战场生存能力,接收机也不容易被敌方发现并干扰,同时双基地雷达散射截面积也有利于对隐身目标的探测[1]。双基地雷达的潜在优势使它在军民用雷达中占有重要地位。近年来,随着卫星导航技术的发展,困扰双基地雷达的时间同步和相位同步等问题逐渐变得易于实现,双基地雷达将有更加广泛的应用。双基地空时自适应处理技术自上世纪90年代末开始成为研究热点,其研究主要集中在收发分置造成的杂波角度多普勒2维谱非独立同分布问题。这是因为双基机载结构下的地面杂波谱(指地杂波相对于接收载机的方位-多普勒谱)形状复杂,并随检测距离发生不规则变化,距离越近,谱变化越剧烈。目前解决双基STAP的杂波非独立同分布问题的核心问题是杂波谱如何对齐。杂波谱对齐的方法主要可以分为两类:第1类通过在多普勒域或角度域补偿训练样本,使其和待检测单元分布相同。这类算法包括多普勒移位法(Doppler Warping,DW)[2];角度-多普勒补偿法(Angle Doppler Compensation,ADC)[2];基于配准的方法(Registration Based Method,RBM)[3]等。这些方法都需要估计或计算杂波多普勒或角度参数,非常复杂。第2类方法利用插值矩阵把杂波样本映射到参考空间,以消除杂波的距离依赖[4]。但要获得插值矩阵,仍需要较大的计算量。近年来不断有新的改进算法提出,以改善上述方法的运算复杂度[5,6]和杂波抑制性能[7,8]。
传统双基地雷达对发射端信息的获取和利用很不充分。发射端信息主要包括发射波形和目标/杂波相对于发射阵列的角度信息。文献[9]提出在双基地雷达中引入多输入多输出(MIMO)技术,从接收数据中同时获取目标相对于接收阵列和发射阵列的角度,从而实现无需距离测量的多目标定位。随后,大量文献对双基地雷达收发角度联合估计方法进行了研究[10-19]。文献[20]进一步把空时自适应处理(STAP)用于双基地MIMO雷达系统中,获得发射空间-接收空间-多普勒3维杂波谱结构,并指出当发射天线和接收天线都是正侧视时,所有距离门的杂波谱聚集在同一个3维平面上。利用正侧视双基地MIMO雷达的杂波共面特性,双基地雷达杂波抑制可以更为简单、灵活。正侧视双基地MIMO雷达可以通过在杂波所在平面形成凹口,以实现空时3维自适应处理(3D-STAP)。这样的3D-STAP滤波器一方面可以直接在杂波所在平面选取样本,从而避免了杂波距离依赖性的补偿问题;另一方面,由于所有距离门的杂波都在同一个平面上,因此这样的滤波器能够有效解决距离模糊对杂波抑制的影响。文献[21-26]分别提出了一些利用双基地MIMO雷达3维杂波共面特征抑制由双基地构形引起的距离依赖杂波的方法。
双基地MIMO雷达也存在一些不利因素:一方面,这一杂波特性的建立在MIMO技术多通道能够理想分离的前提下,要求波形具有理想的自相关与互相关性,但实际上这种理想的波形是不存在;另一方面,MIMO技术带来的虚拟通道数、自由度倍增在提高雷达系统性能的同时,也会导致STAP技术的运算量和需求的样本数倍增,使得双基地MIMOSTAP在实际中很难得到应用。因此,研究双基地MIMO雷达的波形设计以及降维杂波抑制,对于双基地MIMO雷达的工程实现,挖掘双基地MIMO雷达的应用潜力,以及提升现有雷达系统性能具有重要的理论和现实意义。波形设计是MIMO雷达的共性问题,已有大量文献对波形设计研究[27-30]。文献[26]中对双基MIMO-STAP中波形设计问题进行了研究。本文主要综述双基地MIMO雷达3维杂波抑制方法。
2 信号模型及杂波特性
假设接收机的位置坐标是(0,0,Hr),在X-Y平面的垂直投影点 O为坐标系原点,接收机速度Vr的方向与X轴正方向相同。此外,假设发射机的位置坐标是(Lbcosγ,Lbsinγ,Ht),在X-Y平面的投影点为点o。规定X-Y平面内的所有角均是相对于X轴
2.1 双基地MIMO雷达信号模型
双基地MIMO雷达的几何配置如图1所示。正方向的角度,则发射机相对于接收机的方位角为γ,基线Oo的长度为Lb,发射机速度vt的方向与X轴的夹角为φv,接收机和发射机天线阵列轴向的方向分别为φr和φt。定义αi和βi分别是地面上一个距离单元内的第i个杂波散射体相对于接收天线轴向和发射天线轴向的锥角,φr,i和φt,i分别是该杂波散射体相对于接收天线和发射天线的俯仰角,θr,i和θt,i分别是该杂波散射体相对于接收天线轴向和发射天线轴向的方位角。
假设发射机的脉冲重复间隔(PRI)为T,工作波长为λ,一个相关处理间隔(CPI)内发射L个脉冲。发射机和接收机采用阵元数分别为M和N的均匀线阵(ULA),阵元间距分别是dt和dr,且所有阵元均全向地发射窄带脉冲信号。
通过上述几何构形可以得到 MNL× 1维的 3维空时快拍:
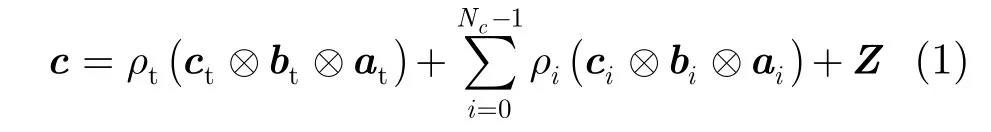
其中,ρt和ρi分别是被目标和第i个杂波散射点反射的回波幅度,不失一般性,假设ρi是均值为零,方差为的独立随机变量,即 ρi~ N(0,);Nc是一个距离单元的杂波点数; Z ∈CNML×1表示噪声成分的充分统计量,并假设它是零均值,协方差矩阵为Q的独立同分布循环对称复高斯随机矢量,即Z~N(0,Q);at,bt和ct分别是目标的接收导向矢量、发射导向矢量和多普勒导向矢量;ai,bi和ci分别是第i个杂波散射点的接收导向矢量、发射导向矢量和多普勒导向矢量。
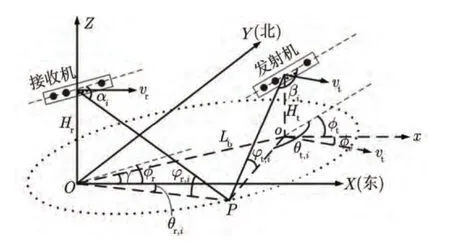
图1 双基地MIMO雷达的几何配置图Fig.1 Geometry of the Bistatic MIMO radar
2.2 正侧视双基地MIMO雷达杂波特性[20]
而且当接收机和发射机均为正侧视情况时,双基地MIMO雷达杂波的多普勒频率fd,i与其接收空间频率fr,i和发射空间频率ft,i的关系式为:
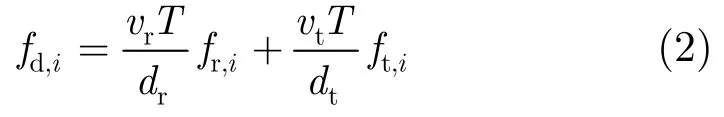
从式(2)可以看出双基地 MIMO 雷达杂波的多普勒频率是其接收空间频率和发射空间频率的函数,且该函数正是3维空间中的平面方程。也就是说杂波脊在接收空间角频率、发射空间角频率和多普勒频率组成的空间内是许多条3维曲线,不同距离单元对应不同谱线,但所有的杂波脊均分布在由接收空间角频率、发射空间角频率以及多普勒频率构成的3维空间中的同一个平面上。且通过式(2)得到这个平面倾斜的角度ψ可以表示为:
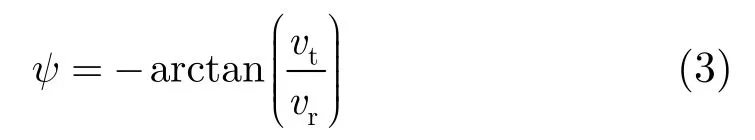
需要特别指出的是,在距离模糊的情况下,由于所有的距离门杂波都在同一个平面上,模糊距离门的杂波仍然在该平面上。这一特性为高脉冲重复频率(PRF)时,解决距离模糊问题提供了新的思路。
图2给出了正侧视情况下双基地MIMO雷达的3维杂波谱。可以看出,当发射阵和接收阵均为正侧视时,双基地 MIMO雷达的杂波谱在发射空间角频率-接收空间角频率-多普勒频率组成的空间内是许多条3维曲线,不同距离单元对应不同谱线,尽管杂波谱具有严重的距离依赖性,但是所有杂波谱线均分布在同一个3维平面上。双基地MIMO雷达杂波谱的这一特性,对双基地雷达系统的杂波抑制有着非常重要的作用。
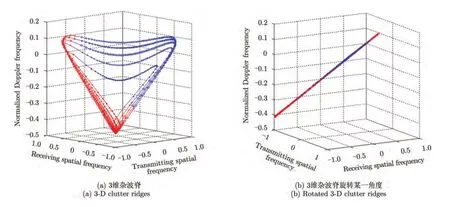
图2 正侧视双基地MIMO雷达杂波脊Fig.2 Bistatic MIMO radar clutter ridges in the side-looking case
3 3维杂波抑制方法
3.1 3D-LCMV
目标回波在接收机处的归一化多普勒频率为:
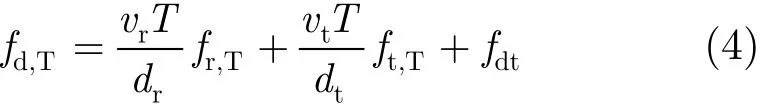
其中fr,T为目标的接收空间角频率,ft,T为目标的发射空间角频率,fdt为目标多普勒。通过对比式(2)与式(4)可以发现,目标和杂波归一化多普勒的区别是目标中存在由目标运动引入的多普勒。因此,只要目标相对于收发天线径向速度和不为零,就可以保证目标不会位于杂波所在的平面上。因此,通过对整个杂波平面进行抑制就可以在实现 3维杂波抑制的同时保留目标。与相控阵雷达中的最小方差约束(LCMV)方法类似,可以通过构造一个 3维线性最小方差(3D-LCMV)滤波器对杂波所在平面进行抑制[22]。
此外,尽管杂波脊仍然是距离依赖的,但是由于每个距离门的杂波都分布在同一个平面上,可以认为这些杂波具有局部的同分布特性。因此,3D-LCMV滤波器求解所需的训练样本可以直接在杂波所在平面选取,这与正侧视单基地相控阵系统是完全一样的。但是,对于该滤波器而言,要实现最优杂波抑制效果需要距离样本是完全 i.i.d.的,而直接从每个距离门选取的训练样本显然不是完全的,因此这样的3D-LCMV滤波器是一个局部最优的滤波器。
利用上述3D-LCMV滤波器能够对空时3维杂波进行抑制,从而实现局部最优的杂波抑制,并且其样本的选取并不需要是i.i.d.的。此外,在距离模糊的情况下,由于所有距离门的杂波都在同一个平面上,模糊距离门的杂波仍然在该平面上,因此通过3D-LCMV滤波器抑制整个平面在距离模糊时的也是同样适用的。综上所述,3D-STAP方法不仅能够获得局部最优的杂波抑制性能,还能够解决双基地雷达的距离模糊问题。
3D-LCMV方法通过有效利用双基地MIMO雷达的发射自由度构建了 3D-STAP滤波器,实现了局部最优的杂波抑制,并且能够消除距离模糊对杂波抑制的影响。但是,该方法计算复杂度高,并且对距离样本数的需求也非常大,导致其在实际中难以实现。针对上述问题,以下介绍几种降维杂波抑制方法。
3.2 3维降维的杂波抑制方法
在传统的单基地相控阵雷达中,降维空时自适应处理方法已经得到了广泛的研究,例如辅助通道方法[31]、广义相邻多波束方法[32]、多通道联合降维方法[33]以及局域化联合处理方法[34]等。但是这些方法都基于检测区域内各距离单元的杂波服从独立同分布,即各训练距离单元回波数据的杂波谱分布相同,而在双基地相控阵雷达中,杂波具有距离依赖特性,需要首先对杂波的距离依赖特性进行补偿预处理,而距离依赖特性补偿的性能也决定了这些降维方法的杂波抑制性能。利用由发射空间频率-接收空间频率-多普勒频率构成3维空间内的杂波脊聚集在同一个平面上这一特点,把传统降维空时自适应处理方法推广到3维情况,这些方法可实现局部最优的杂波抑制,而不需要经过距离依赖特性补偿[24]。
3.2.1 3维辅助通道方法(3D-ACR) 3维辅助通道方法的工作原理是首先通过 3维快速傅里叶变换(FFT)将雷达空时接收数据由发射阵元-接收阵元-脉冲域转换到接收波束-发射波束-多普勒域,然后在这个3维波束域空间内选取杂波所在的全部3维波束作为辅助通道,结合目标所在波束进行3维自适应处理。
3维辅助通道的选取有多种方法,下面对特征矢量波束选取法进行描述。在双基地MIMO雷达信号模型基础上,对杂波加噪声的协方差矩阵RC+N做特征值分解为:
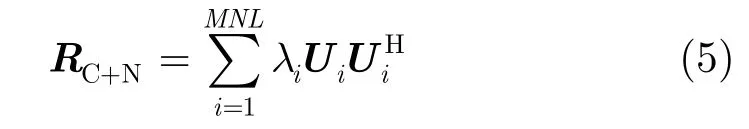
其中,λi为协方差矩阵的第i个特征值,Ui为其对应的归一化特征向量。当噪声为零均值高斯白噪声时,MNL个特征值具有如下特性:
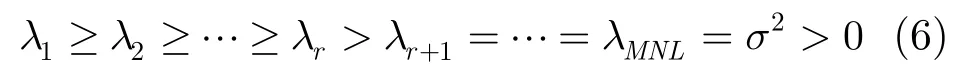
其中,r为大特征值个数,σ2为高斯白噪声功率。特征值λ1,λ2,…,λr及其对应的特征矢量U1,U2,…,Ur反应了杂波的特性信息,即特征矢量U1,U2,…,Ur构成了杂波子空间。则可利用杂波子空间构造 MNL×(1+r)阶降维矩阵 T3D-ACR:
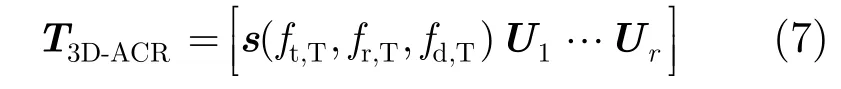
3维辅助通道方法对接收数据做降维处理后,协方差矩阵的维数由MNL降为(1+r),相应的杂波协方差矩阵求逆运算量由O(M3N3L3)降 为O((1+r)3),对独立同分布杂波样本数目的要求由2×MNL降为 2×(1+r)。通常情况下,单基地MIMO雷达杂波加噪声协方差的大特征值个数为M+N+L,在双基地MIMO雷达系统下其个数虽然会有所增加,但(1+r)≪ MNL,因此,3维辅助通道方法大大降低了求逆运算量。需要指出的是,3维辅助通道方法的杂波抑制性能会由于降维产生一定的损失。而且,由于需要对MNL维协方差矩阵做特征值分解,因此3维辅助通道方法仍然要求一定的独立同分布杂波样本数目来估计协方差矩阵,且运算量仍然十分巨大。
3.2.2 3维局域化联合处理 与多通道降维方法类似,局域化联合降维方法[19]同样出现在单基地相控阵STAP系统中,同样适用于单基地MIMO雷达系统中,且都是局部最优的 3维杂波抑制方法。3维局域化降维杂波抑制方法是通过选取目标附近的发射波束、接收波束和多普勒通道来构造降维矩阵。类似地,在双基地MIMO雷达信号的基础上,本文方法仍是按照上述方法获得空时数据矢量,但对降维矩阵的构造方法进行了改进,改为构造MNL×RMRNRL阶局域化降维矩阵TJDL:
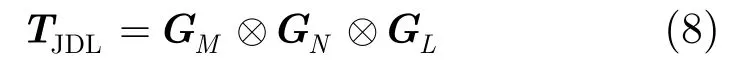
其中,RM,RN,RL为分别构造降维矩阵时选取的发射波束、接收波束以及多普勒通道的数目。发射降维矩阵可以表示为:
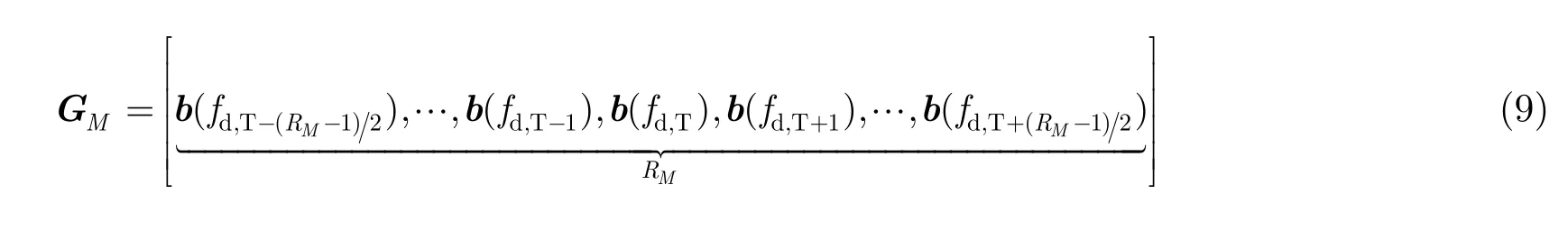
其中,b(ft,T−rm),b(ft,T+rm)为目标发射波束附近第 rm(rm=1,2,…,(RM−1)/2)个波束的发射阵列导向矢量(−rm表示左移rm个通道,+rm表示右移rm个通道)。接收降维矩阵可以表示为:
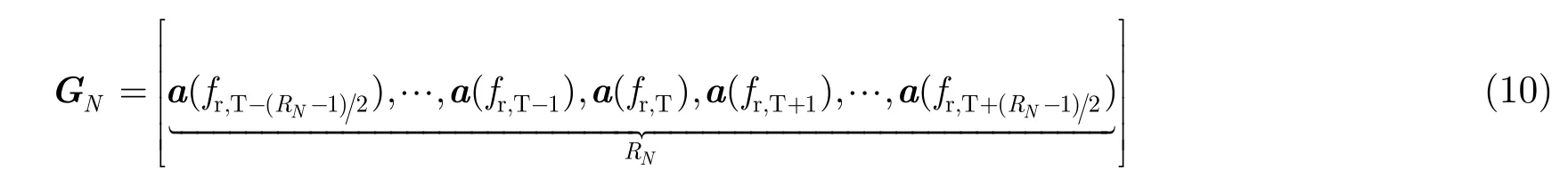
其中,a(fr,T−rn),a(fr,T+rn)为目标接收波束附近第 rn(rn=1,2,…,(RN−1)/2)个波束的接收阵列导向矢量。多普勒降维矩阵可以表示为:
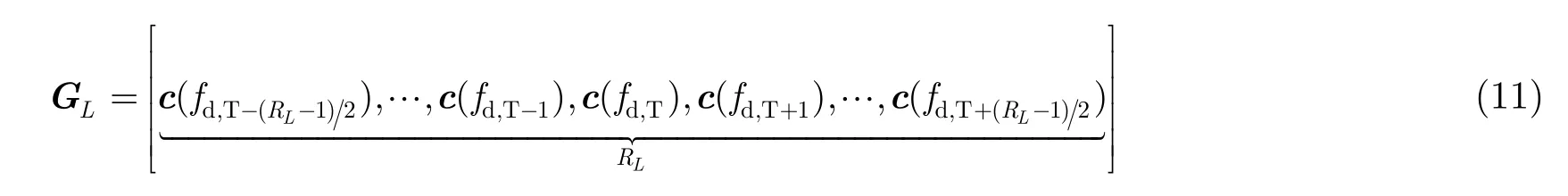
其中,c(fd,T−rl),c(fd,T+rl)为目标多普勒通道附近第rl(rl=1,2,…,(RL−1)/2)个通道的多普勒导向矢量。
3维局域化降维杂波抑制方法中,协方差矩阵的维数由MNL降为RMRNRL,RM,RN和RL分别为选取的发射波束、接收波束以及多普勒通道的数目,则相应的求逆运算量由O(M3N3L3)降为O(),使独立同分布杂波样本数目的要求由2×MNL降为2×RMRNRL。3D-JDL方法选取的 3维波束数目越少,其在样本数充足时的性能越差,但其运算量以及需求的均匀样本数目也越少,因此3D-JDL方法需要结合实际杂波样本的数目以及运算处理的能力来选择合适的3维波束数目。
3.2.3 性能比较 本小节通过仿真对正侧视双基地MIMO雷达系统下的 3维线性最小方差方法(3D-LCMV)、3维辅助通道方法(3D-ACR)、3维局域化联合处理方法(3D-JDL)、3维多通道联合处理方法(3D-mDT)以及 3维广义相邻多波束法(3DGMB)的杂波抑制性能进行了对比和分析。仿真参数选取如下:发射机和接收机均采用正侧视MIMO雷达,M=8,N=8,K=8,λ=0.3 m,PRF= 2000 Hz,杂噪比为40 dB,Lb=100 km,接收机高度为Hr=9 km,接收机速度为Vr=100 m/s,接收机速度方向为0°,发射机高度为 Ht=10 km,发射机速度为vt=100 m/s,发射机速度方向为90°。3D- ACR方法选取的杂波协方差特征向量数为30,3D-GMB方法选取的目标附近发射波束方向、接收波束方向和多普勒通道方向的3维波束数目都为6,3D-JDL选取的发射波束数为 RM=3,接收波束数为 RN=3,多普勒通道数为 RK=3。图3给出了几种降维的3维杂波抑制方法,可以看出,这些降维方法能够有效提高小样本条件下的双基地 MIMO雷达距离依赖杂波抑制性能。
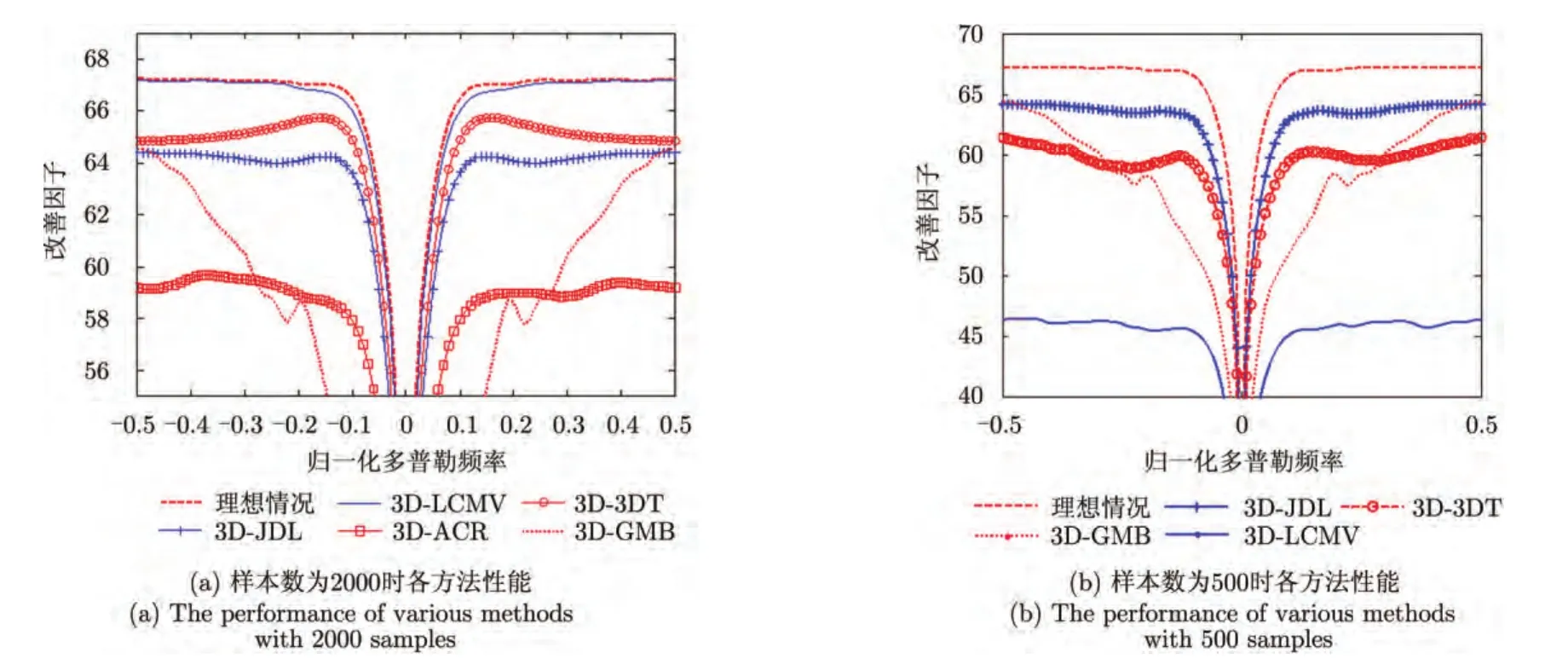
图3 降维的3维杂波抑制方法性能Fig.3 Performance of the reduced dimensional 3-D clutter suppression methods
3.3 3维投影方法
上述降维方法通过降低自由度的方式来降低计算量和需求的样本数,其本质是构造降维矩阵,在波束域进行降维处理,性能损失比较大。针对这一问题,本节介绍一种基于3维投影降维的机载双基地MIMO雷达杂波抑制方法。如图4所示,该方法利用正侧视双基地MIMO雷达杂波脊的共面特性,通过3维投影将3维杂波转换为2维杂波,从而获得i.i.d.训练样本,其本质是在数据域进行降维处理,将正侧视双基地MIMO雷达杂波转换为单基地相控阵杂波,来消除杂波的距离依赖特性,性能损失比较小。
根据几何3维投影原理可知,一个平面在与其法线方向平行的任一平面上的投影是一条直线。也就是说,通过选择合适的投影方向,就可以将平面上的所有杂波投影到同一条直线上,从而使得不同距离门的杂波是非距离依赖的,实现最优的空时自适应处理。3维杂波投影的坐标变换公式为:
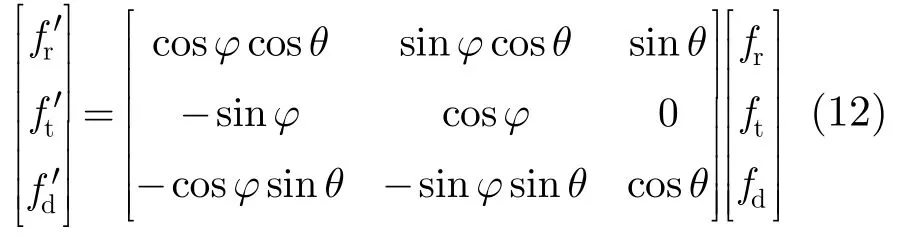
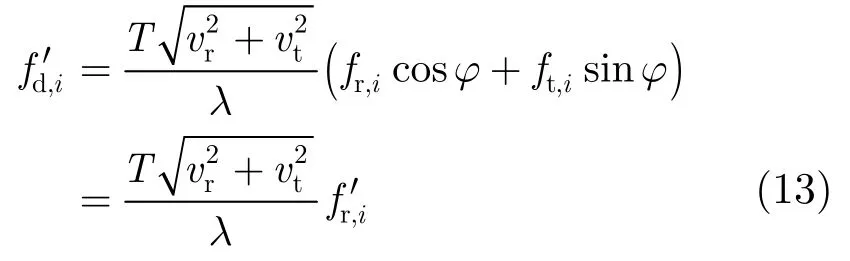
从式(13)可以看出,新坐标系下的多普勒频率与接收空间频率呈线性关系。利用式(12)可以得到新坐标系下的杂波脊为如图5所示。
以上的变换仅仅是几何上对杂波脊的处理,实际处理中需要利用空时插值方法构建3维投影矩阵,来将接收数据进行投影实现降维处理。然而,这样的3维投影矩阵需要对 MNL×Nc维的空时导向矢量矩阵做求伪逆运算,所需计算量约为(M NL)3+(M NL)2×Nc,巨大的计算量会给实时处理带来不便。下面再介绍一种基于虚拟发射波束形成的方法拟合3维投影矩阵。
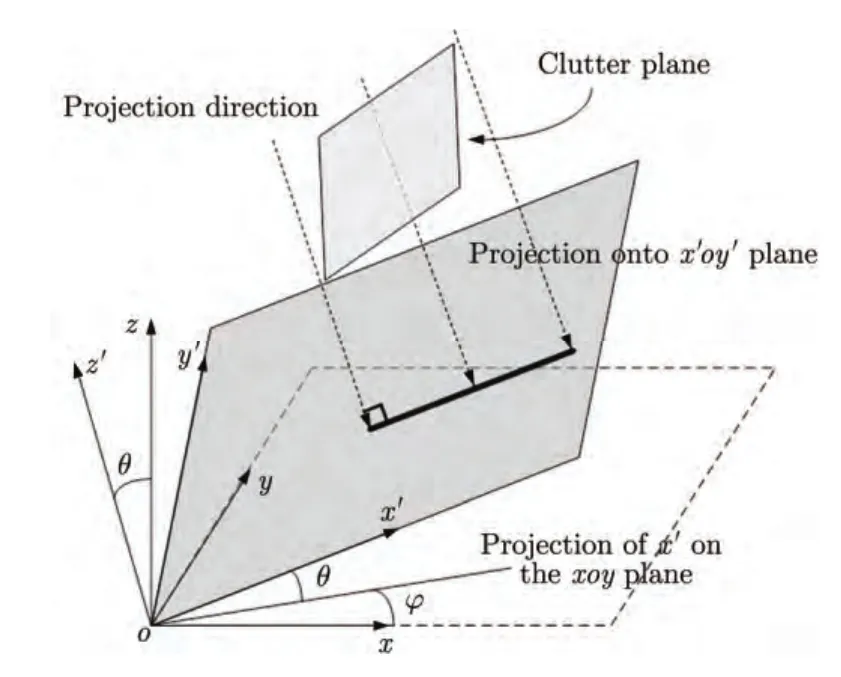
图4 3维投影原理Fig.4 Principle of the 3-D projection
该方法首先对接收数据进行旋转,获得在新坐标系下的接收数据cP:
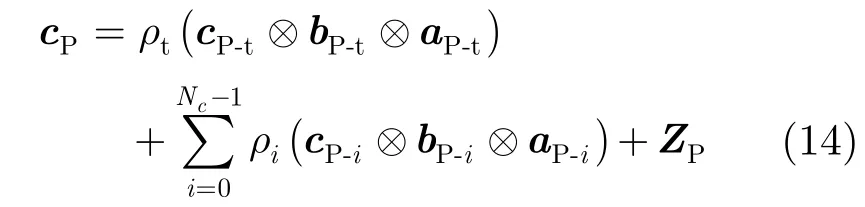
其中,aP-t,bP-t和cP-t分别是新坐标系下目标的接收导向矢量、发射导向矢量和多普勒导向矢量;aP-i,bP-i和cP-i分别是新坐标系下第i个杂波散射点的接收导向矢量、发射导向矢量和多普勒导向矢量,ZP表示新坐标系下噪声成分的充分统计量。
然后通过对接收数据引入一个虚拟发射波束形成来实现3维投影过程,式(14)变为:
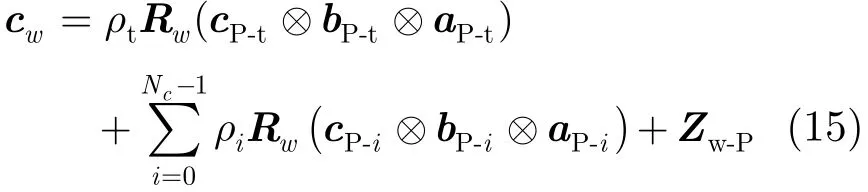
此外,发射波束权的选择会影响该方法的杂波抑制性能,因此需要对该权值进行优化设计。由于最大化输出 SINR等价于在高斯噪声背景中最大化检测概率,因此可以通过如下约束问题对发射波束权进行优化:
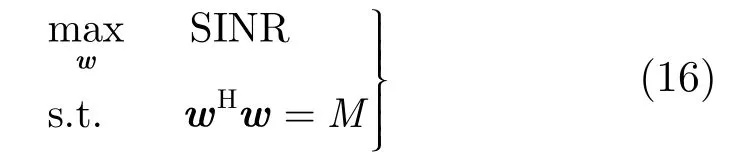
其中SINR为式(8)构造的输出信干噪比[23]。在此基础上,采用半正定规划对式(16)进行求解,优化方法参见文献[23]。另外,也可根据空时插值原理,通过将式(15)的杂波脊分布拟合为图4中的杂波脊分布,对发射波束权进行求解:
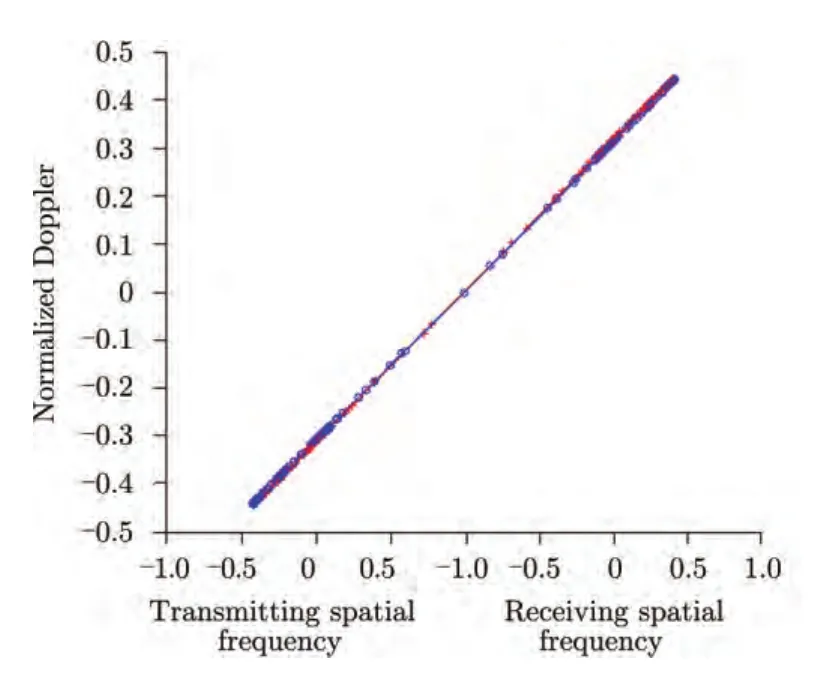
图5 新坐标系下杂波脊Fig.5 The clutter ridges in the new coordinates system
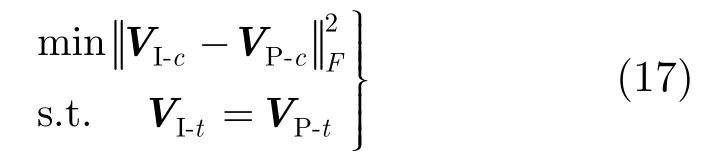
其中,VI-c,VI-t和VP-c,VP-t分别为图4和式(8)中得到的杂波分布和目标导向矢量。具体求解方法参见文献[26]。下面给出3种不同虚拟发射权值的3维投影杂波抑制性能,并与传统的双基地相控阵杂波抑制进行比较。
图6(a)采用空时插值方法设计的虚拟发射权,图6(b)采用对权值进行优化后的虚拟发射权,图6(c)采用随机方向投影的虚拟发射权。从图6(a)可以看出,机载双基地MIMO雷达杂波谱被变换为正侧视单基地相控阵杂波谱,不再具有距离依赖性,但是由于仍然存在一定的模糊。而利用一些先验信息对虚拟发射权优化后,从图6(b)中可以看出这些模糊得到了有效的抑制。观测图6(c)可以看出,未经过虚拟发射权优化设计的权尽管也能够将主杂波转换为一条直线,但是其旁瓣杂波非常强,严重影响了杂波抑制性能。图6(d)为传统双基地相控阵没有经过距离依赖补偿的杂波谱。3维投影方法的优化方法及性能参见文献[21,23,26]。
4 总结和展望
双基地MIMO雷达通过对接收数据的处理同时获得目标相对于发射阵列和接收阵列的角度,从而能够使得空时杂波谱呈现出发射空间-接收空间-多普勒3维杂波谱结构。特别是在正侧视条件下,所有距离门的杂波聚集在一个3维平面上。此时,只要目标相对于收发天线径向速度之和不为零,目标就不会位于杂波所在平面,因此通过构建3D-LCMV滤波器在杂波平面处形成凹口即可实现距离依赖杂波抑制。在此基础上,本文还介绍了由传统降维STAP推广得到的3维降维方法,包括3维辅助通道方法、3维广义相邻多波束方法、基于多通道联合处理、局域化联合处理等。最后,介绍了3维投影降维的双基地MIMO雷达杂波抑制方法。这些方法可有效提高小样本数下的机载正侧视双基地MIMO雷达杂波抑制性能,使机载双基地雷达的杂波抑制变得更为简单、灵活。尽管在双基地MIMO雷达参数估计/定位方面,国内外已经有大量的研究结果发表[9-19],但针对双基地MIMO雷达地面动目标检测的研究刚刚开始,公开的文献主要是由本项目组发表的几篇原始文献,有必要吸引更多的研究小组参与到相关主题的研究与讨论中,以加快双基地MIMO雷达地面动目标检测基本理论和方法的研究。
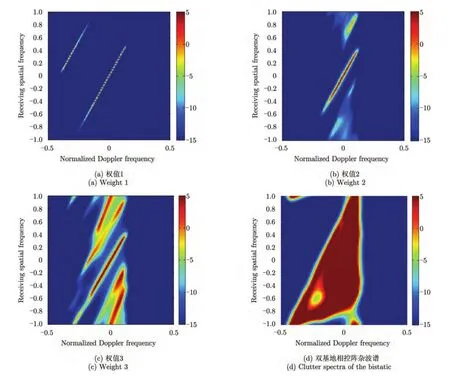
图6 3维投影杂波抑制方法杂波谱对比Fig.6 Comparison of the clutter spectra of different 3-D projection methods
初步研究已经揭示出双基地MIMO雷达在地面动目标检测中的一些优势,但其潜在优势和存在的问题还有待于进一步揭示。尤其对发射端信息如何进一步充分利用,包括如何利用发射端空间和波形信息,结合知识辅助方法提高复杂环境下空时自适应处理的性能还有巨大的研究空间。最近,Baker等人[35]进一步把双基MIMO-STAP雷达模型[20]推广到多站相干MIMO-STAP模型。由于未来的雷达正在向网络化发展,而网络雷达的基本单元就是双基体系,因此对双基MIMO-STAP的研究也将对雷达网络化提供理论基础和推进动力。
[1]Willis N J and Griffiths H D.Advances in Bistatic Radar[M].SciTech Publishing,Raleigh,NC,2007.
[2]Himed B,Zhang Y,and Hajjari A.STAP with angle-Doppler compensation for bistatic airborne radars[C].IEEE Radar Conference,Long Beach,California,2002: 311-317.
[3]Lapierre F D,Verly J G,and Van Droogenbroeck M.New solutions to the problem of range dependence in bistatic STAP radars[C].IEEE Radar Conference,Huntsville,AL,2003: 452-459.
[4]Varadarajan V and Krolik J L.Joint space-time interpolation for distorted linear and bistatic array geometries[J].IEEE Transactions on Signal Processing,2006,54(3): 848-860.
[5]Beau S and Marcos S.Range dependent clutter rejection using range-recursive space-time adaptive processing (STAP)algorithms[J].Signal Processing,2010,90(1): 57-68.
[6]杨博,黄知涛,周一宇.基于变换域的双基地 STAP 距离独立性补偿方法[J].电子学报,2010,38(6): 1366-1370.Yang Bo,Huang Zhi-tao,and Zhou Yi-yu.Rangedependence compensation method based on transformation for bistatic stap[J].Acta Electronica Sinica,2010,38(6):1366-1370.
[7]Colone F.Spectral slope-based approach for mitigating bistatic space-time adaptive processing clutter dispersion[J].IET Radar,Sonar & Navigation,2011,5(5): 593-603.
[8]彭晓瑞,谢文冲,王永良.一种基于空时内插的双基地机载雷达杂波抑制方法[J].电子与信息学报,2010,32(7): 1697-1702.Peng Xiao-rui,Xie Wen-chong,and Wang Yong-liang.Improved joint space-time interpolation technique for bistatic sirborne radar[J].Journal of Electronics & Information Technology,2010,32(7): 1697-1702.
[9]Yan Hai-dong,Li Jun,and Liao Gui-sheng.Multitarget identification and localization using bistatic MIMO radar systems[J].EURASIP Journal on Advances in Signal Processing,2008,2008: 48.
[10]Chen Duo-fang,Chen Bai-xiao,and Qin Guo-dong.Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12): 770-771.
[11]Jin Ming,Liao Gui-sheng,and Li Jun.Joint DOD and DOA estimation for bistatic MIMO radar[J].Signal Processing,2009,89(2): 244-251.
[12]Chen Jing-li,Gu Hong,and Su Wei-min.A new method for joint DOD and DOA estimation in bistatic MIMO radar[J].Signal Processing,2010,90(2): 714-718.
[13]Bencheikh M L,Wang Y,and He H.Polynomial root finding technique for joint DOA DOD estimation in bistatic MIMO radar[J].Signal Processing,2010,90(9): 2723-2730.
[14]Zhang X,Xu Z,Xu L,et al..Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar[J].IET Radar,Sonar &Navigation,2011,5(6): 626-631.
[15]张剑云,郑志东,李小波.双基地 MIMO 雷达收发角及多普勒频率的联合估计算法[J].电子与信息学报,2010,32(8):1843-1848.Zhang Jian-yun,Zheng Zhi-dong,Li Xiao-bo.An algorithm for DOD-DOA and Doppler frequency jointly estimating of bistatic MIMO radar[J].Journal of Electronics & Information Technology,2010,32(8): 1843-1848.
[16]Li J and Zhang X.Improved joint DOD and DOA estimation for MIMO array with velocity receive sensors[J].IEEE Signal Processing Letters,2011,18(12): 717-720.
[17]张永顺,郭艺夺,赵国庆,等.MIMO 双基地雷达空间多目标定位方法[J].电子与信息学报,2010,32(12): 2820-2824.Zhang Yong-shun,Guo Yi-duo,Zhao Guo-qing,et al..Multitarget localization in three dimensions for MIMO bistatic radar[J].Journal of Electronics & Information Technology,2010,32(12): 2820-2824.
[18]Chen H,Li X,and Zhuang Z.Antenna geometry conditions for MIMO radar with uncoupled direction estimation[J].IEEE Transactions on Antennas and Propagation,2012,60(7): 3455-3465.
[19]Tang Bo,Tang Jun,Zhang Y,et al..Maximum likelihood estimation of DOD and DOA for bistatic MIMO radar[J].Signal Processing,2012,93(5): 1349-1357.
[20]Li Jun,Liao Gui-sheng,and Hugh G.Bistatic MIMO radar space-time adaptive processing[C].2011 IEEE Radar Conference,Kansas City,Missouri,2011: 498-502.
[21]Li Jun,Liao Gui-sheng,and Hugh G.Range-dependent clutter cancellation method in bistatic MIMO-STAP radars[C].2011 IEEE CIE International Conference,Chengdu,2011,1: 59-62.
[22]Wu J,Wang T,Zhang L,et al..Range-dependent clutter suppression for airborne sidelooking radar using MIMO technique[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(4): 3647-3654.
[23]党博,廖桂生,李军,等.基于投影权优化的双基地 MIMO 雷达杂波抑制方法[J].电子与信息学报,2013,35(10): 2505-2511.Dang Bo,Liao Gui-sheng,Li Jun,et al..Weighted projection optimization for range-dependent clutter suppression in bistatic MIMO radar[J].Journal of Electronics &Information Technology,2013,35(10): 2505-2511.
[24]刘长赞.机载双基地 MIMO雷达距离依赖杂波抑制方法研究[D].[硕士论文],西安电子科技大学.2014.Liu Chang-zan.Research on airborne bistatic MIMO radar range-dependent clutter suppression[D].[Master dissertation],Xidian University,2014.
[25]李焕.双基地MIMO雷达目标检测与定位方法研究[D].[硕士论文],西安电子科技大学,2013.Li Huan.Reseatch of target detection and localization for bistatic MIMO radar[D].[Master dissertation],Xidian Unniverisity,2013.
[26]党博.机载双基地MIMO雷达波形设计与空时自适应处理研究[D].[博士论文],西安电子科技大学,2013.Dang Bo.Space-time adaptive processing and waveform design for air-borne bistatic MIMO radar[D].[Ph.D.dissertation],Xidian University,2013.
[27]公绪华,孟华东,魏轶旻,等.杂波环境下面向扩展目标检测的自适应波形设计方法[J].清华大学学报(自然科学版),2011,51(11): 1742-1746.Gong Xu-hua,Meng Hua-dong,Wei Yi-min,et al..Adaptive waveform design for range-spread target detection in clutter[J].Journal of Tsinghua University (Science &Technology),2011,51(11): 1742-1746.
[28]Friedlander B.Waveform design for MIMO radars[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3): 1227-1238.
[29]Chen C Y and Vaidyanathan P P.MIMO radar ambiguity properties and optimization using frequency-hopping waveforms[J].IEEE Transactions on Signal Processing,2008,56(12): 5926-5936.
[30]Dang Bo,Li Jun,and Liao Gui-sheng.Taylor polynomial expansion based waveform correlation cancellation for bistatic MIMO radar localization[J].Signal Processing,2012,92(6): 1404-1410.
[31]Klemm R.Adaptive airborne MTI: an auxiliary channel approach[J].IEE Proceedings-F: Communications,Radar and Signal Processing,1987,134(3): 269-276.
[32]Wang Y L,Chen J W,Bao Z,et al..Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(1): 70-81.
[33]廖桂生.相控阵天线 AEW 雷达时空二维自适应处理[D].[博士论文],西安电子科技大学,1992.Liao Gui-sheng.Space-time adaptive processing for phased array AEW radar[D].[Ph.D.dissertation],Xidian University,1992.
[34]Wang H and Cai L.On adaptive spatial-temporal processing for airborne surveillance radar systems[J].IEEE Transactions on Aerospace and Electronic Systems,1994,30(3): 660-670.
[35]Bell K L,Johnson J T,Baker C J,et al..Modeling and simulation for multistatic coherent MIMO radar[C].2013 IEEE Radar Conference,Ottawa,2013: 1-6.

