不同转子齿数电励磁分块转子磁通切换电机谐波特性影响的对比研究
连广坤, 郭卉, 顾国彪
(1.中国科学院 电工研究所,北京 100190;2.中国科学院大学,北京 100049)
0 引言
早在19世纪50年代学者S.E.Rauch就提出了磁通切换的概念[1],之后将这一原理应用于旋转电机的研究一直没有间断,直到法国学者E.Hoang于1997年提出三相永磁式磁通切换电机之后[2],以其结构简单坚固、无不可逆退磁危险和弱磁能力强等的优势引起了国内外学者的广泛关注,新型的磁通切换电机的拓扑形式不断被提出,从励磁方式上来划分,有电励磁、永磁励磁和混合励磁型磁通切换电机,在电动汽车、航空电源和风力发电等领域展现出了良好应用前景[3-11]。
电励磁分块转子磁通切换电机(electrical excitation segmented-rotor flux-switching machines,ESFSM)就是在这样的背景下,由英国纽卡斯尔大学B.C.Mecrow教授带领的课题组将磁通切换的原理应用于分块转子开关磁阻电机而提出来的,并以12/8结构原理样机为例,通过理论和实验对该电机的电磁特性进行了深入研究,并建立了基于dq轴的等效数学模型,研究结果表明该电机可工作于无刷交流控制方式,其转矩密度与开关磁阻电机相当,在低成本驱动领域有一定的应用前景[12-14]。国内,南京航空航天大学针对电励磁分块转子磁通切换电机功率密度低和永磁式分块转子磁通切换电机调磁困难的缺陷,提出了一种新型的混合励磁分块转子磁通切换电机并对其电磁特性和调磁能力进行了细致的研究[15]。总体来说,分块转子磁通切换电机作为一种新型的电机拓扑,尚处于实验室理论研究阶段,但由于其结构简单、风摩和油摩损耗小等特点,使其在低成本和高速电机领域展现出了良好的应用前景。
1 ESFSM电机结构
电励磁分块转子磁通切换电机的结构如图1所示,可见电机结构与分块转子开关磁阻电机的结构完全相同,但ESFSM电机的定子绕组分为电枢绕组和励磁绕组两部分,图中的F1~F6即为励磁绕组,且满足相邻的励磁线圈电流方向相反,电机工作时,通入一定的直流励磁电流,其余6个线圈构成ABC三相电枢绕组,其转子由若干个扇形铁心块嵌套在不导磁的转子套中组成。
可见,相对于常规电励磁磁通切换电机,定子结构更为简单。本文以文献[12]中优化设计的原理样机作为研究对象,该电机的主要参数为:定子齿数Ps=12;额定电流IN=14 A;额定转速nN=500 r/min;定子铁心外径Dso=150 mm;定子轭厚hz=11 mm;定子内径Dsi=91.2 mm;定子齿宽hs=12.5 mm;定子极弧系数αs=0.833;转子外径Dr=90.6 mm;转子齿厚hr=14 mm;定转子铁心有效长度la=150 mm;励磁线圈匝数Nf=44;电枢线圈匝数Ne=44。
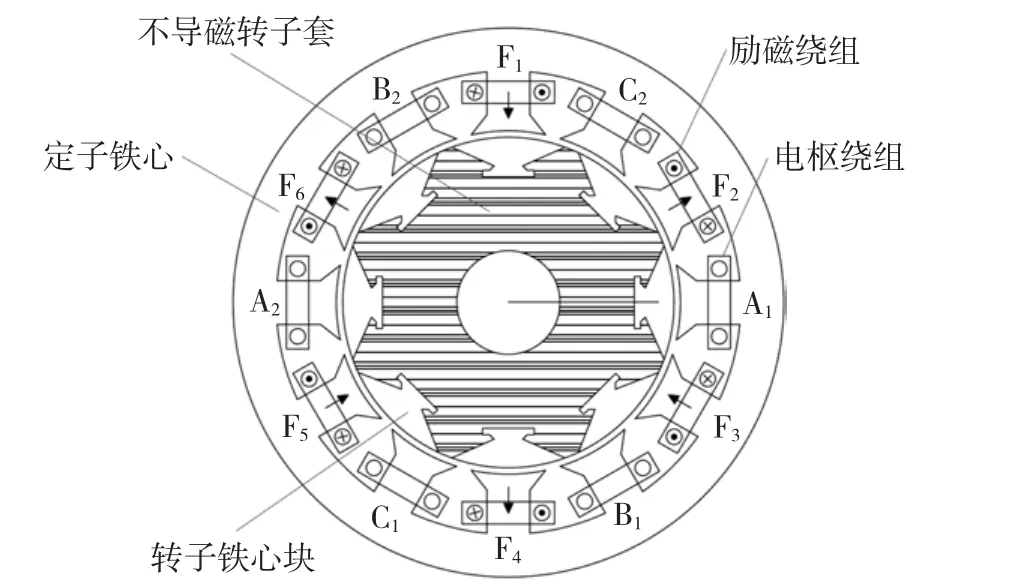
图1 ESFSM电机结构Fig.1 Configuration of ESFSM
2 ESFSM电机工作原理
假设电励磁分块转子磁通切换电机工作时励磁绕组F1~F6按如图1所示的方向通入直流励磁电流,定义磁通穿入线圈时为正,以线圈A1为例进行分析。
ESFSM电机工作原理如图2所示。

图2 ESFSM电机工作原理Fig.2 Operation principle of the ESFSM machines
当转子齿处于如图2(a)所示的位置时,由最小磁阻原理可知磁通穿出线圈A1,即A1匝链负磁通;当转子齿处于如图2(b)所示的位置时,磁通穿入线圈A1,即A1匝链正磁通;则当转子连续旋转时线圈A1匝链的磁通正负周期变化,这就是ESFSM电机磁通切换的工作原理[12-15]。
3 谐波特性对比分析
ESFSM作为三相电机工作,转子齿数需满足3个条件:1)定子齿数Ps为6的倍数;2)转子齿数Pr不能被Ps/2整除,Nr也不能整除Ps/2;3)转子齿数Pr不能同时被3整除[14]。
从原理上来讲,满足以上3个条件的任何转子齿数均可使电机作为三相电机工作。从文献[12-14]的研究结果中可以看出,当Ps=12时,转子齿数Pr选择在Ps/2-2~Ps/2+2范围内时,电机具有较高的转矩密度和反电势,由于本文以定子12齿为例进行研究,因此转子齿数取4、5、7和8。后续研究表明12/4、12/8有相同的谐波特性,而12/5和12/7有相同的谐波特性,因此本文选取12/7和12/8两种结构为例对比研究分析电机的谐波特性。
由于ESFSM电机为双凸极结构,因此转子转动过程中,定子齿与转子存在齿齿正对、齿槽正对和非正对3种位置关系,定义为P1~P3,分析当P1或P2时,该定子齿所对应线圈匝链的磁通为零,而处于P3时匝链有效磁通,为了后续分析方便,定义匝链正、负磁通最大位置分别为位置PA1和PA2。ESFSM电机的极对数即为转子齿数Pr,所以12/7和12/8结构的一个电周期转子分别转动51.43°和45°,图3和图4给出了两种结构电机一个运行周期的4种典型位置。
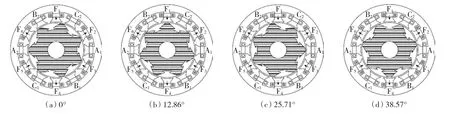
图312 /7结构ESFSM电机4个典型位置Fig.3 Four typical location of the 12/7 ESFSM
根据如图3和图4所示的位置关系可以得到两种结构电机磁链的变化曲线,如图5(a)所示,由图中相对位置变化可以看出,12/7结构的A1和A2两个线圈大小变化趋势随时间一致,所对应的齿相对转子位置变化方向相反,即A1的磁链ψA1和A2的磁链ψA2满足

如果将ψA1和ψA2展开为傅里叶级数形式,即

式中:ψmi为磁链第i次谐波的幅值;wi为磁链第i次谐波的角频率;φi为磁链第i次谐波的相位。
则A相磁链为

由图5(b)可以得到12/8结构A1和A2两个线圈大小变化趋势相反,即满足

则A相磁链为
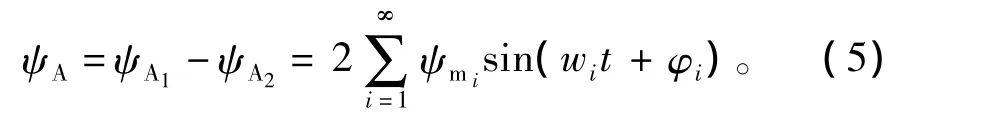
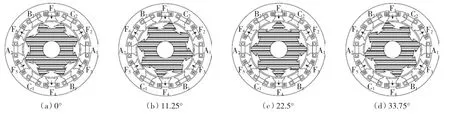
图412 /8结构ESFSM电机4个典型位置Fig.4 Four typical location of the 12/8 ESFSM
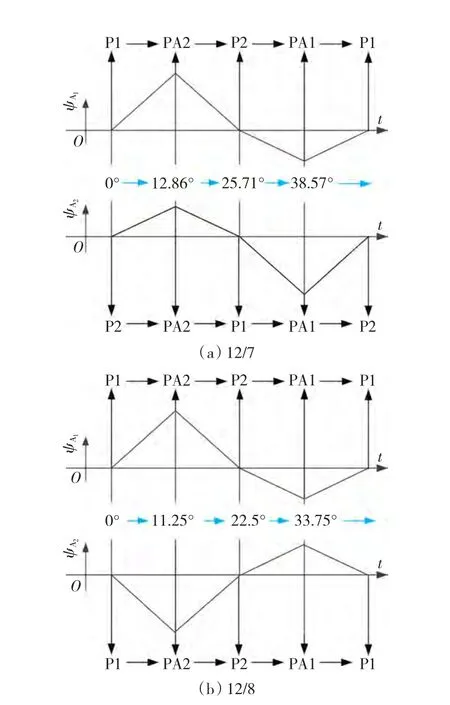
图5 两种结构电机磁链的原理波形Fig.5 Pattern of excitation of 12/7 and 12/8 ESFSM
由式(1)~式(3)可知,12/7结构电机每相的两个线圈的磁链基波和奇数次谐波相互叠加,而偶数次谐波相互抵消,因此12/7结构电机不含有偶数次谐波,由式(4)和式(5)可知,12/8结构电机一相的两个线圈仅是磁链仅是符号相反,无抵消偶数次谐波的特性。反电势与磁链分析方法相同,且具有相同的性质。
4 有限元仿真验证
参照文献[12]中的设计的原理样机的参数,仅对电机转子齿极弧系数按照磁链幅值最大的目标优化,最终得到12/7、12/8结构电机的转子极弧系数均为分0.85。
建立两种结构电机的有限元仿真模型,提取电机的线圈A1、线圈A2和A相磁链和空载反电势,分别如图6和图7所示,由图可知两种电机任一个线圈(如A1)的磁链和反电势关于过零点不对称,即

式中:θ为电机转子角位置;T为电机的转子周期角。
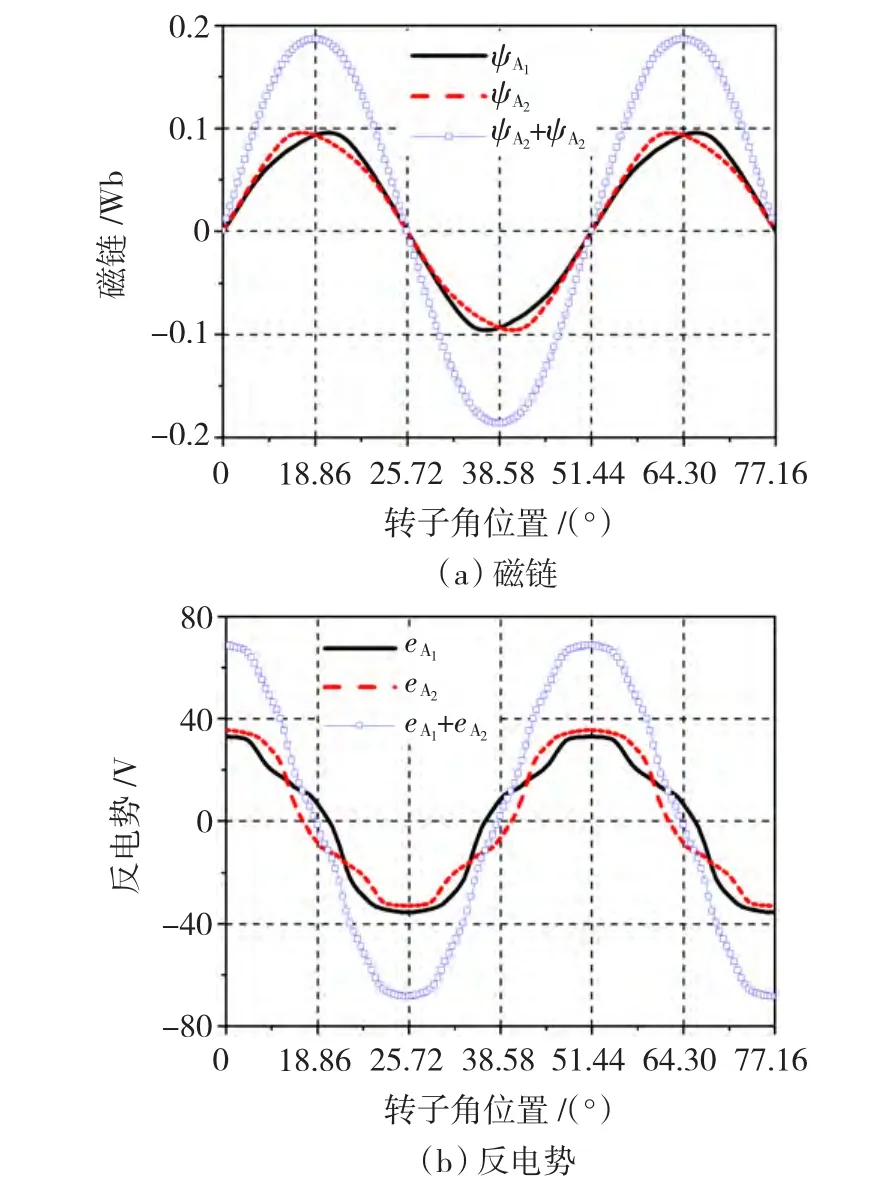
图612 /7结构ESFSM电机的磁链和反电势Fig.6 Flux-linkage and back-EMF of 12/7 ESFSM

图712 /8结构ESFSM电机的磁链和反电势Fig.7 Flux-linkage and back-EMF of 12/7 ESFSM
所以单个线圈的磁链和反电势均不为转子角位置上的奇谐函数,又由于两者均无直流分量,因此磁链和反电势中必含有大量偶次谐波,即磁链和反电势的正负半周期波形的不对称性是由偶数次谐波引起的。对提取的12/7和12/8两种结构电机的磁链和反电势进行傅里叶分解,结果分别如图8和图9所示,取前16次谐波计算单根线圈及相绕组的总谐波失真(total harmonic distortion,THD),并分离出奇数次和偶数次谐波含量,结果如表1和表2所示,计算的公式为
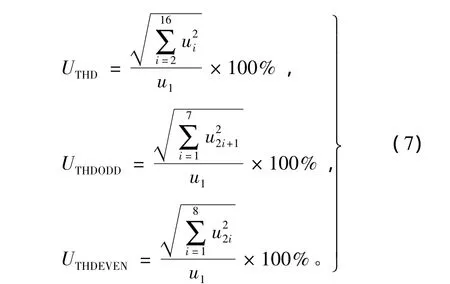
式中,ui为第i次谐波的幅值。

图812 /7结构的磁链和反电势的谐波分布Fig.8 Harmonics of flux-linkage and back-EMF for 12/7 motor

图912 /8结构磁链和反电势的谐波分布Fig.9 Harmonics of flux-linkage and back-EMF for 12/8 motor
由图8和图9所示的谐波分布特性可知,两种结构电机的单个线圈的磁链和反电势中均含有大量偶次谐波,同时从图中可以看出12/7结构电机一相的两根线圈的偶数次谐波相互抵消,即合成的A相绕组仅含有奇数次谐波,且为时间的奇谐函数,即正负半周是对称的。而12/8结构电机中的奇数次和偶数次谐波均叠加,没有抵消作用,验证了上文的理论分析的正确性。
由表1和表2的计算结果可知,两种结构电机的单根线圈磁链和反电势的偶数谐波含量远大于奇数次谐波含量,因此有抵消偶数次谐波作用的12/7结构电机的THD远小于12/8结构电机,同时可以看出12/7结构电机磁链和反电势的基波幅值也大于12/8结构,即性能优于12/8结构。
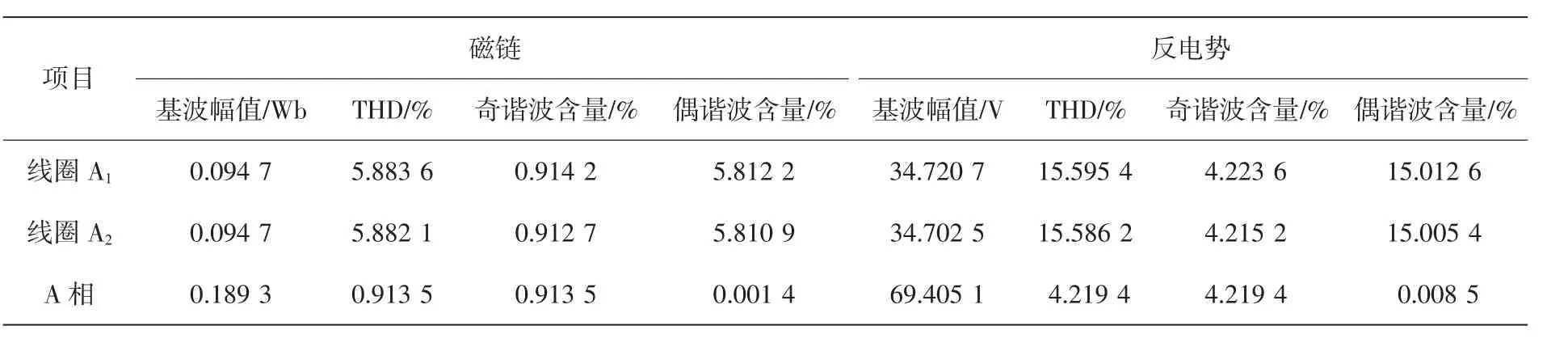
表112 /7结构电机的谐波特性Table 1 Harmonic character of 12/7

表212 /8结构电机的谐波特性Table 2 Harmonic character of 12/8
5 结语
针对一种新型的电励磁分块转子磁通切换电机,以12/7和12/8两种结构电机为例,对比研究了不同极数对电机的谐波分布特性的影响,研究结果表明12/7结构的磁链和反电势中没有偶数次谐波,采用有限元法提取了两种结构电机的磁链和反电势,求得THD并分离奇数和偶数次谐波含量,验证了理论分析的正确性。研究结果表明,转子极数对ESFSM电机磁链和反电势的谐波分布具有重要的影响,在电机设计时需根据设计目标合理选择。本文采用的研究方法可以推广至任何定子齿数的三相分块转子磁通切换电机的谐波特性的分析。
本文的研究方法和研究结论,为分块转子型磁通切换电机设计时转子齿数选择提供了理论依据,为该电机的研究发展奠定了基础。
[1]RAUCH S E,JOHN L J.Design principles of flux-switching alternators[J].AIEE Transactions,1955,74(3):1261-1268.
[2]HOANG E,GABSI M,LECRIVAI N,et al.Influence of magnetic
losses on maximum power limits of synchronous permanent magnet drivers in flux-weakening mode[C]//2000 IEEE Industry Applications conference,October 8-12,Rome,Italy.2000,1:299-303.
[3]ZHU Z Q.Switched flux permanent magnet machine-innovation continues[C]//2011 International Conference on Electric Machine and System,August 20-23,2011,Beijing,China.2011:1-10.
[4]ZHU Z Q,CHEN J T.Advanced flux-switching permanent magnet brushless machines[J].IEEE Transactions on Magnetics,2010,46(6):1447-1453.
[5]花为,程明,ZHU Z Q,等.新型磁通切换型双凸极永磁电机的静
态特性研究[J].中国电机工程学报,2006,26(13):129-134.
HUA Wei,CHENG Ming,ZHU Z Q,et al.Study on static characteristics of novel flux-switching doubly-salient PM machines[J].Proceedings of the CSEE,2006,26(13):129-134.
[6]HUA W,CHENG M,ZHANG G.A novel hybrid excitation fluxswitching motor for hybrid vehicles[J].IEEE Transactions on Magnetics,2009,45(10):4728-4731.
[7]王宇,邓智泉,王晓琳.新型电励磁磁通切换电机励磁绕组结构分析[J].中国电机工程学报.2011,31(24):97-104.
WANG Yu,DENG Zhiquan,WANG Xiaolin.Analysis of the field windings setting pattern for the novel electrical excitation fluxswitching machine[J].Proceedings of the CSEE,2011,31(24):97-104.
[8]黄志文,沈建新,方宗喜,等.用于弱磁运行的三相6/5极永磁
开关磁链电机的分析与优化设计[J].中国电机工程学报.2008,28(30):61-66.
HUANG Zhiwen,SHEN Jianxin,FANG Zongxi,et al.Analysis and optimal design of 3-pahse 6/5 pole PM flux-switching motor for flux-weakening application[J].Proceedings of the CSEE,2008,28(30):61-66.
[9]WANG Y,DENG Z Q.Improved stator flux estimation method for direct torque linear control of parallel hybrid excitation switchedflux generator[J].IEEE Transactions on Magnetics,2012,27(3):747-756.
[10]颜建虎,林鹤云,冯奕.磁通切换型横向磁通风力发电机[J].中国电机工程学报,2010,30(21):67-72.
YAN Jianhu,LIN Heyun,FENG Yi.Flux switching transverse flux permanent wind generator[J].Proceedings of the CSEE,2010,30(21):67-72.
[11]朱婷婷,邓智泉,王宇.并列式混合励磁磁通切换型电机及其矢量控制策略研究[J].中国电机工程学报,2012,32(15):140-147.
ZHU Tingting,DENG Zhiquan,WANG Yu.Research on hybridexcited flux-switching machine and the current vector control strategy[J].Proceedings of the CSEE,2012,32(15):140-147.
[12]ZULU A,MECROW B C,ARMSTRONG M.A wound-field three phase flux-switching synchronous motor with all excitation sources on the stator[J].IEEE Transactions on Industrial Applications,2010,46(6):2363-2371.
[13]ZULU A,MECROW B C,ARMSTRONG M.Investigation of the dq-Equivalent model for performance prediction of flux-switching synchronous motors with segmented rotors[J].IEEE Transactions on Industrial Electronics,2012,59(6):2393-2402.
[14]ZULU A,MECROW B C,ARMSTRONG M.Topologies for wound-field three-phase segmented-rotor flux-switching machines[C]//5th IET International Conference on Power Electronics,Machines and Drives,April 19-21,2010,Brighton,UK.2010:1-6.
[15]熊树,邓智泉,王宇,等.混合励磁分块转子磁通切换电机电磁特性分析[J].电机与控制学报.2012,16(10):51-57.
XIONG Shu,DENG Zhiquan,WANG Yu.Electromagnetic performance analysis for hybrid excitationsegmented-rotor flux-switching machines[J].Electric Machines and Control,2012,16(10):51-57.

