一种永磁同步电机的失磁故障重构方法研究

何静， 张昌凡， 贾林， 李祥飞， 赵凯辉，3

(1.湖南工业大学电气与信息工程学院，湖南株洲 412007;2.国防科技大学机电工程与自动化学院，湖南长沙 410073;3.中南大学交通运输工程学院，湖南长沙 410075)

永磁同步电机的磁链方程为

0 引言

电机是现代传动中机电能量转换的核心部件，其性能很大程度上决定了传动系统的品质。近年来永磁同步电机得到了越来越广泛的应用，人们对它的运行安全性和可靠性也提出了越来越高的要求［1］。与异步电动机等电励磁电机相比，永磁同步电机最大的问题在于永磁材料存在失磁风险。而永磁体的磁场波动或失磁都会直接导致电机发热异常及转矩性能变差，严重时电机可能报废［2］，这一问题极大地限制了永磁电机的应用范围［3］。

针对永磁同步电机的失磁问题，目前最常采用的解决方法是从电机设计角度出发，优化磁路结构，降低失磁风险。这种基于静态预防的解决方案效果有限，并需增加电机制造成本。对于电机运行过程中产生的失磁，则往往要等到引发明显故障后才会停机检测，而此时的失磁程度通常已经非常严重，因此这种情况下的检测，只能称之为失磁后的离线分析方法。为能够及早消除故障隐患，确保永磁电机的安全可靠运行，有必要进行永磁同步电机失磁故障的在线检测与诊断的研究。

针对永磁同步电机的实时失磁检测问题，Kang等对单相永磁电机，提出了一种不可逆失磁状况的预估方法［4］，但它属于开环估计，对预估的失磁程度没有通过反馈环节来检验。Shinnaka提出一种基于“D－Module”的磁链观测法［5］，Chen等提出一种改进的反电势法［6］，但这两种方法都只能监测固定方向的磁链幅值波动。针对隐极式永磁同步电机，郎宝华、肖曦提等出一种基于卡尔曼滤波器的永磁体磁链在线监测方法［7－8］。针对智能故障检测算法，Gritli、文传博等分别提出一种基于小波算法在线监测算法［9－10］，Lu等提出基于人工神经网络失磁故障检测方法［11］。

快速而高效失磁故障检测算法是能在工程实际应用的基础。为此，本文针对内置式永磁同步电机，将算法简单，鲁棒性强的滑模(sliding mode)观测器［12］和龙伯格(Luenberger)观测器相结合，基于滑模等值控制原理对永磁体磁链进行了实时监测，并给出了其失磁故障的重构算法以及仿真实验结果。

1 系统的描述

在固定于转子永磁体磁场方向的d－q坐标系下，永磁同步电机电压方程为［13］

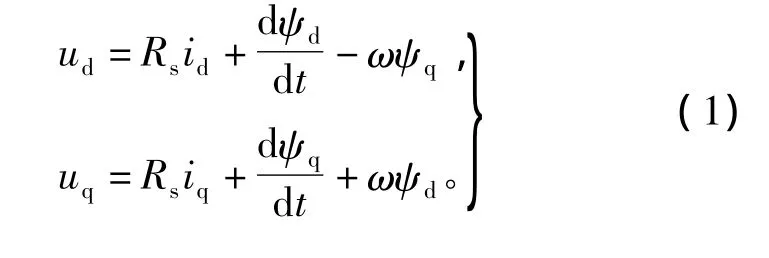
永磁同步电机的磁链方程为

式中:Rs为定子绕组相电阻;Ld、Lq分别为定子绕组的d－q轴电感;ud、uq分别为定子绕组的d－q轴电压;id、iq分别为定子绕组的d－q轴电流;ψd、ψq分别为d－q坐标系中定子磁链分量;ψr为转子永磁体磁链;ω为转子电角速度。

当永磁电机发生失磁故障，而导致永磁体磁链矢量幅值和方向发生如图1变化时，相应式(2)的磁链方程变为

式中:ψrd、ψrq为永磁体磁链在d－q轴下分别产生新的磁链分量。

图1 内置式永磁同步电机永磁体磁链的变化Fig.1 Variation of IPMSM flux

把式(3)分别带入式(1)可以得电压方程为

2 状态观测器设计及故障重构

选取定子电流作为状态变量，由式(5)可得失磁情况下永磁同步电机d－q坐标系下的状态方程为

式中:x，u，y，fa分别为状态变量、系统输入、系统输出、失磁故障，其定义为

由于A和D阵包含转子电角速度，式(6)为一个时变状态方程。另外，从工程角度考虑，永磁体磁链应为有界的，故可假设失磁故障fa有界，即存在一个正常值F，使‖fa‖≤F。

本节利用可测输入u及可测输出y，设计状态观测器以对实现失磁故障fa进行重构。

对式(6)所述系统设计如下滑模观测器和龙伯格观测器，即

由式(6)与式(7)可得观测器误差方程为

那么当选择适当k和L时，则由式(8)确定的观测器误差方程将收敛到零。

观测器收敛性证明:

选取如下正定函数作为Lyapunov函数

由式(8)并对式(9)求导得

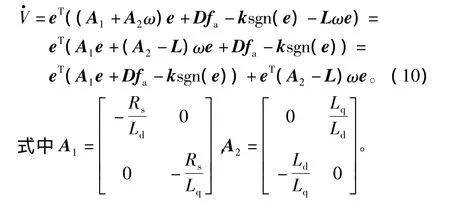
式中k3=min{k1，k2}

当设计k3≥F‖D‖+η，其中 η＞0，则由式(11)得

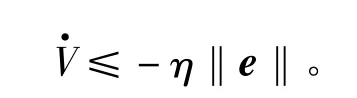
由Lyapunov稳定性理论可知:所设计的观测器式(7)渐进稳定。

当系统状态到达滑模面后e，根据滑模等值控制原理［14］，有e==0，故由式(8)可得

式中veq是不连续项v的等效输出注入值。

取[k1k2]T=ω，其中=[]T为大于零的常值矩阵，则由式(12)得估计永磁体磁链算式为且有A=A1+A2ω。

由式(8)和式(10)可看出，当设计L=A2时，可隔离系统矩阵A中ω的变化对观测器误差方程造成影响。进一步由式(10)得

为减少滑模运动的抖动，采用连续函数取代符号函数，由此构造如下失磁故障重构算法

式中δ1，δ2均为大于零的微小常数。

3 仿真与分析

基于观测器的永磁同步电机矢量控制系统如图2所示。采用id=0的控制策略。控制系统框图包括速度调节器、电流调节器、位置和速度检测、状态观测器以及失磁故障重构等模块。仿真所用永磁同步电机参数如表1所示。根据前述设计方法，其观测器和故障重构模块参数分别为:δ1=0.01，δ2=0.01==300。设状态变量初值均为零，观测器状态变量初值为(0)=1.5 A，(0)=15 A。

图2 控制系统框图Fig.2 Block diagram of control system

表1 电机参数标称值Table 1 The nominal value of the motor parameters

下面分4种情况讨论:

情况1:无失磁。在0～0.1 s时系统处于空载;0.1 s加3 N阶跃型负载转矩。速度给定值为300 r/min。图3～图5分别给出了电机速度的实际值跟踪其给定值、观测定子相电流和永磁体总磁链的仿真波形。

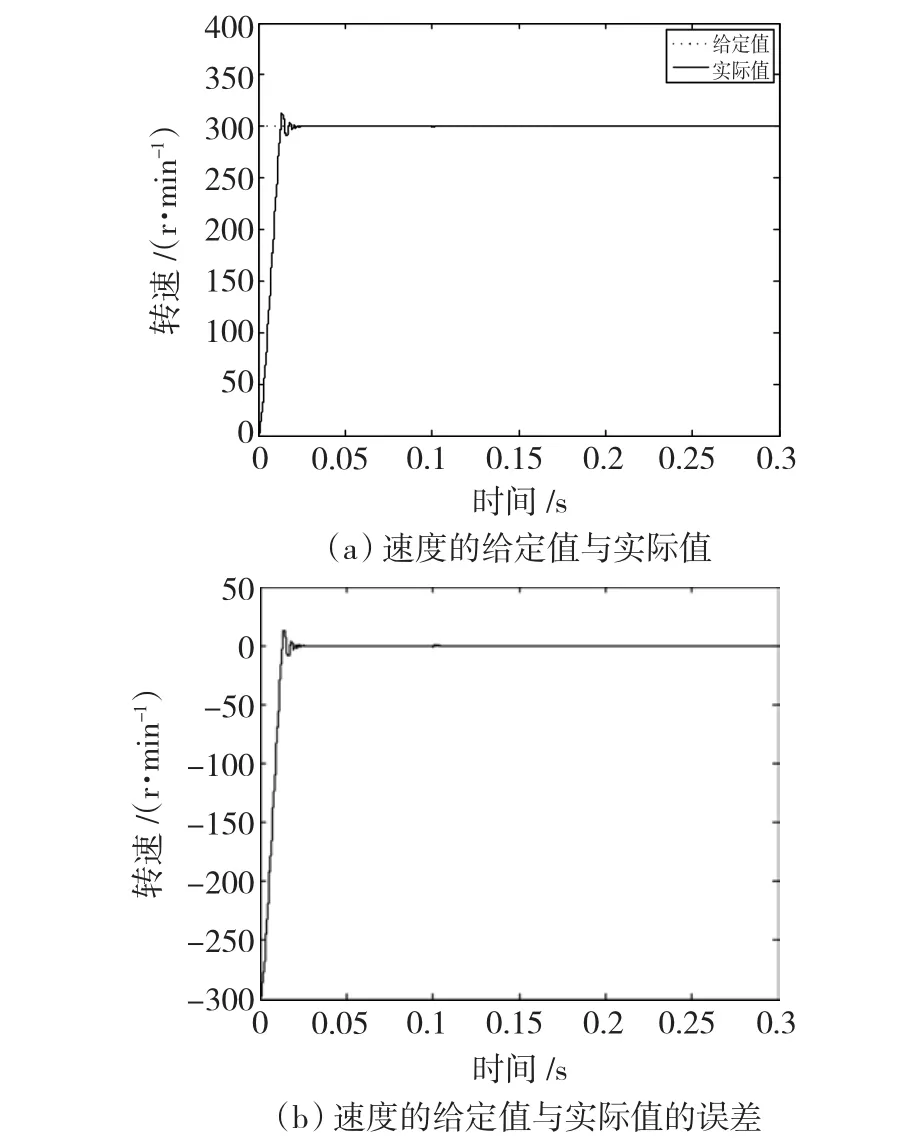
图3 速度的给定值与实际值及其跟踪误差Fig.3 The set＆real value of speed and the tracking error

图4 定子ABC相电流的实际值与观测值及其观测误差Fig.4 The real＆observing of stator current and their error

图5 永磁体总磁链的实际值与观测值及其观测误差Fig.5 The real＆observing of flux and their error

从图3～图5可看出，由于系统采用id=0的控制策略，速度能快速跟踪其给定值，定子电流和磁链观测值也能迅速跟踪相应实际值。

情况2:仅发生幅值失磁，即在0.1 s，转子磁链幅值由0.175 Wb变为0.15 Wb。同时在起动就加3 N负载转矩。为了更直现反映系统过渡过程，下面给出d－q轴相应变量波形。图6、图7分别给出了观测定子d－q轴电流的仿真波形，图8、图9分别给出了观测转子d－q轴磁链的仿真波形。

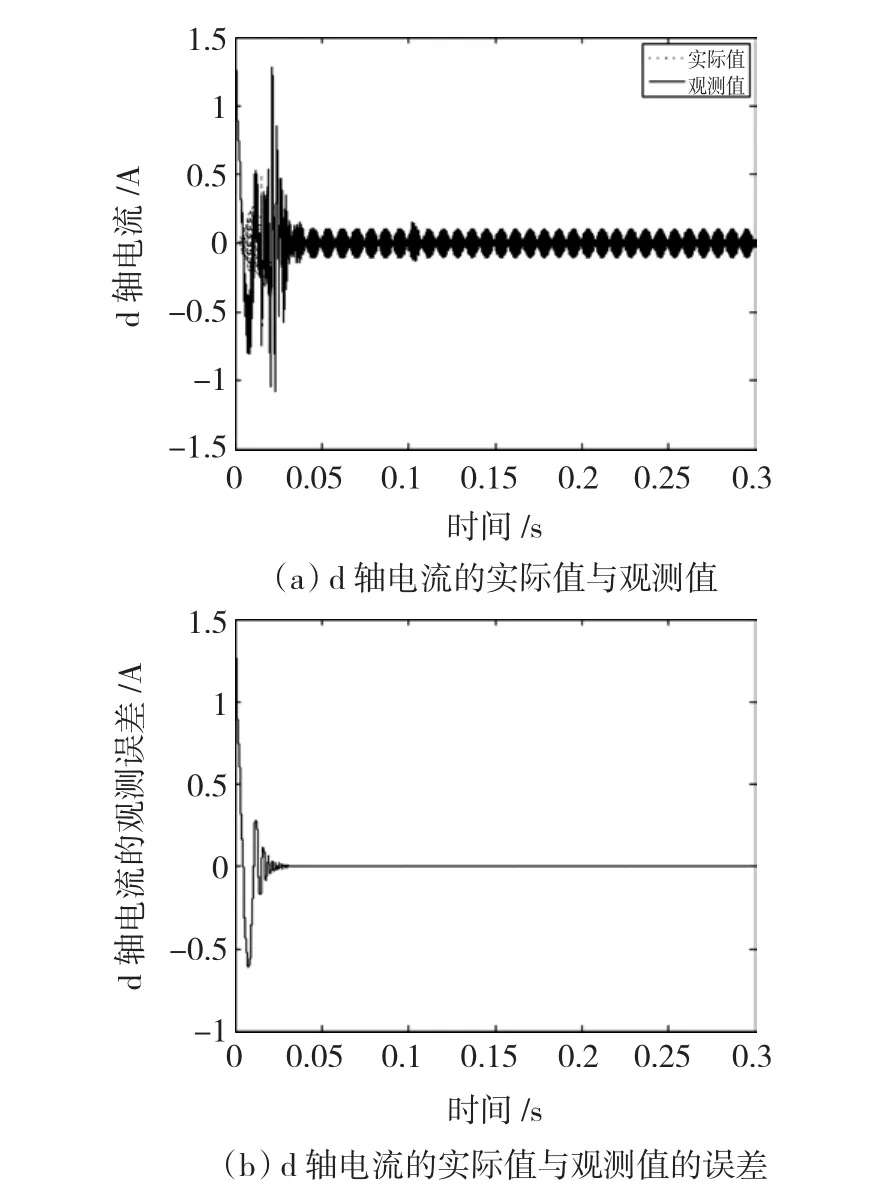
图6 定子d轴电流的实际值与观测值及其观测误差Fig.6 The real＆observing of d-axis current and their error

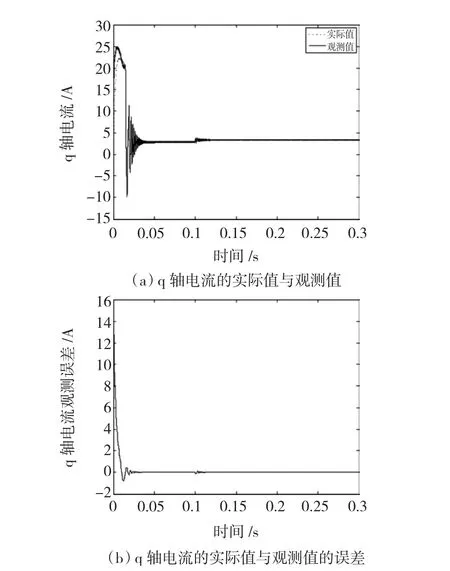
图7 定子q轴电流的实际值与观测值及其观测误差Fig.7 The real＆observing of q-axis current and their error

图8 d轴转子磁链的实际值与观测值及其观测误差Fig.8 The real＆observing of d-axis flux and their error

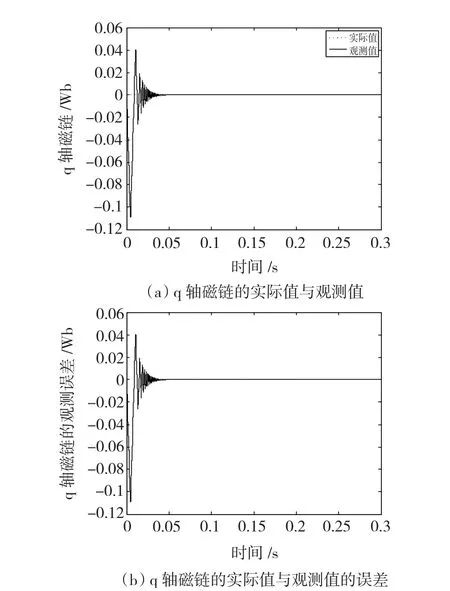
图9 q轴转子磁链的实际值与观测值及其观测误差Fig.9 The real＆observing of q-axis flux and their error

情况3:既有幅值失磁，又有角度失磁，即在0.1 s时，转子d轴磁链由0.175 Wb变为0.15 Wb，图1中位置偏差γ由0 rad变为π/6 rad。同时在起动就加5 N负载转矩。图10、图11分别给出了观测定子d－q轴电流的仿真波形。图12、图13分别给出了观测转子d－q轴磁链的仿真波形。

图10 定子d轴电流的实际值与观测值及其观测误差Fig.10 The real＆observing of d-axis current and their error

图11 定子q轴电流的实际值与观测值及其观测误差Fig.11 The real＆observing of q-axis current and their error

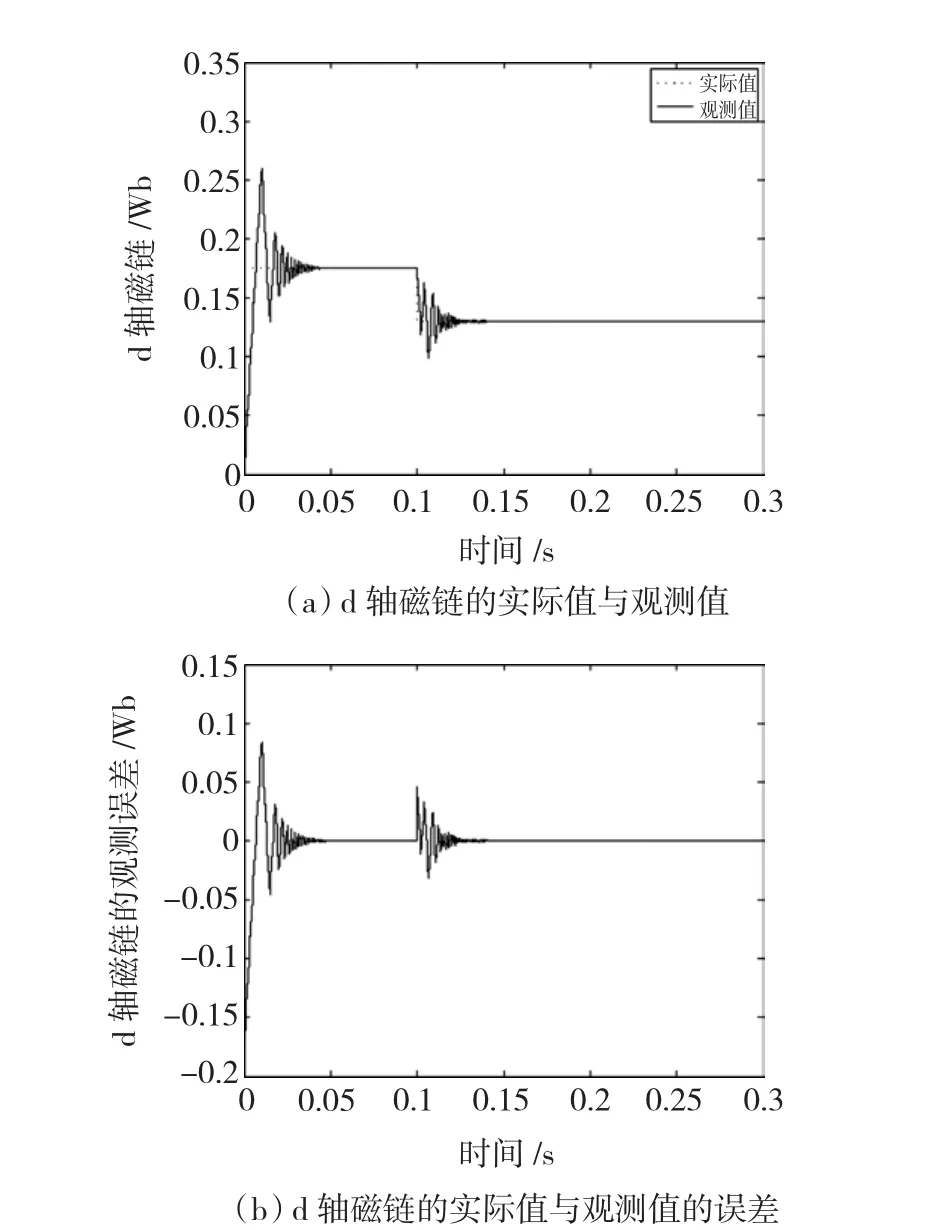
图12 d轴转子磁链的实际值与观测值及其观测误差Fig.12 The real＆observing of d-axis flux and their error

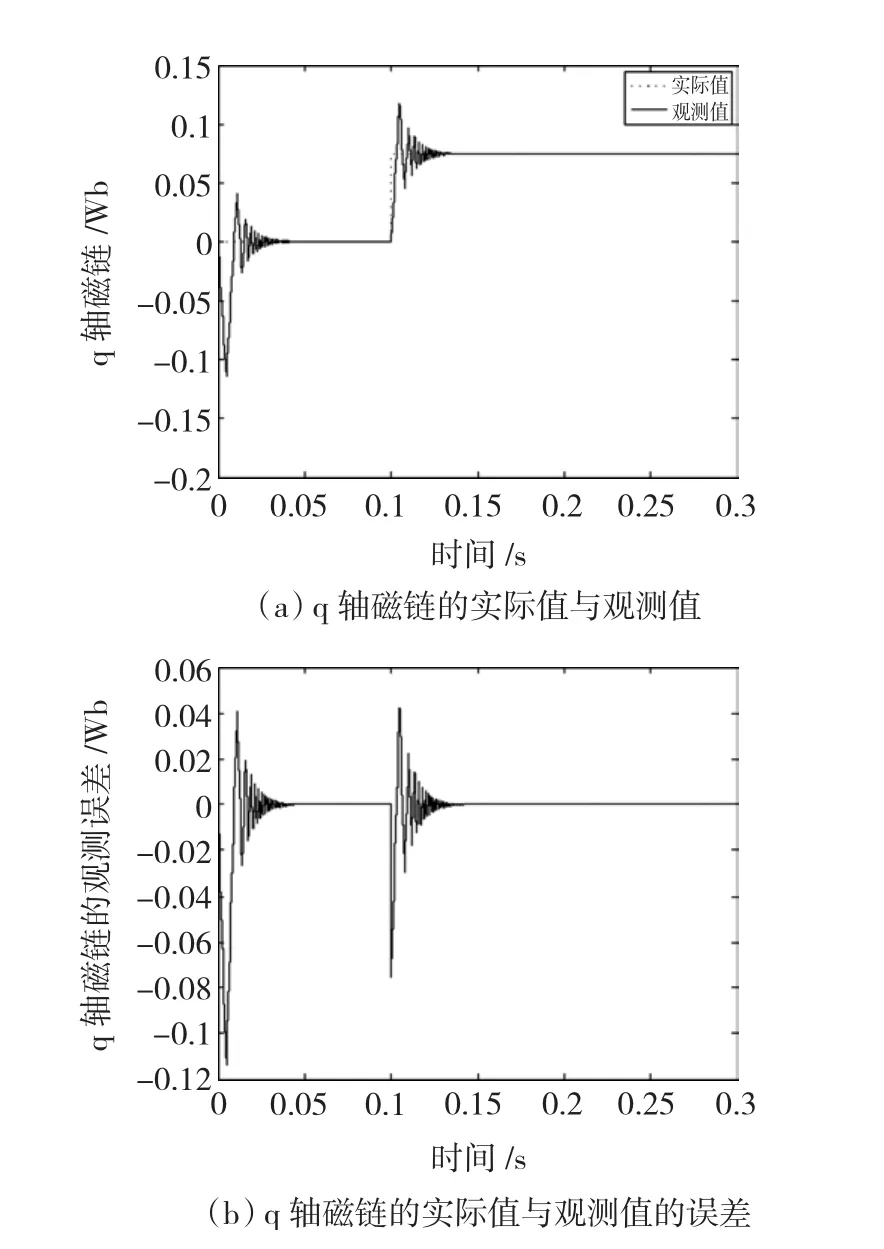
图13 q轴转子磁链的实际值与观测值及其观测误差Fig.13 The real＆observing of q-axis flux and their error

从上述情况2和3的仿真波形可看出，d、q轴磁链观测值能准确跟踪实际值，表明观测器可快速收敛至磁链的准确方向和幅值。

情况4:速度给定值在0.1 s时，由300 r/min变为500 r/min;式(14)中故障观测器参数修改为:¯k1=¯k2=300+100sin(100t);失磁与负载转矩情况同情况3。图14为观测永磁体总磁链的仿真波形。

图14 永磁体总磁链的实际值与观测值及其观测误差Fig.14 The real＆observing of flux and their error

对比情况4中的图14，当速度给定值发生变化，¯k1和¯k2值在200～400呈正弦变化吋，永磁体总磁链的实际值与观测值误差也能收敛到零点。这也同时说明本文提出的故障重构算法的参数选择方便。

4 结语

提出一种基于双观测器的内置式永磁同步电机失磁故障检测方法。建立了同步旋转坐标系下永磁同步电机失磁故障数学模型。构建了龙伯格观测器，以隔离系统矩阵中电机速度变化对观测器误差方程造成影响。设计了滑模变结构观测器，以实现永磁体的失磁故障检测。同时，由于是基于滑模等值控制原理对失磁故障进行实时重构，因此算法简单，鲁棒性强，滑模变结构观测器参数选择方便。实验结果验证了该方法的正确性和有效性。

［1］丁荣军.现代轨道牵引传动及控制技术研究与发展［J］.机车电传动，2010(5):1－8.

DING Rongjun.The research and development of modern railway traction and control technology［J］.Electric Drive for Locomotives，2010(5):1－8.

［2］VINSON G，COMBACA M，PRODO T，et al.Permanent magnets synchronous machines faults detection and identification［C］//38th Annual Conference on IEEE Industrial Electronics Society(IECON)，Oct 25－28，2012，Montreal，Canada，2012，3925－3930.

［3］冯江华.轨道交通永磁同步牵引系统的发展概况及应用挑战［J］.大功率变流技术，2012(3):1－7.

FENG Janghua.Development overview and application challenges of permanent magnet synchronous traction system for rail transit［J］.High Power Converter Technology，2012(3):1－7.

［4］KANG GyuHong，HUR Jin，NAM Hyuk，et al.Analysis of irreversible magnet demagnetization in line-start motors based on the finite-element method［J］.IEEE Transactions on Magnetics，2003，39(3):1488－1491.

［5］SHINNAKA S.New“D-state-observer”based vector control for sensorless drive of permanent-magnet synchronous motors［J］.IEEE Transactions on Industry Applications，2005，41(3):825－833.

［6］CHEN Zhiqian，TOMITA M，DOKI S，et al.An extended electromotive force model for sensorless control of interior permanent-magnet synchronous motors［J］.IEEE Transactions on Industrial E-lectronics，2003，50(2):288－295.

［7］郎宝华，刘卫国，王永强.基于卡尔曼滤波器的永磁同步电机定子磁链观测研究［J］.中国电机工程学报，2007，40(6):17－20.

LANG Baohua，LIU Weiguo，WANG Yongqiang.Observation study of stator flux linkage of permanent magnet synchronous motor based on kalman filter［J］.Proceedings of the CSEE，2007，40(6):17－20.

［8］肖曦，张猛，李永东.永磁同步电机永磁体状况在线监测［J］.中国电机工程学报，2007，27(24):43－47.

XIAO Xi，ZHANG Meng，LI Yongdong.On-line estimation of permanent-magnet flux linkage ripple for PMSM［J］.Proceedings of the CSEE，2007，27(24):43－47.

［9］GRITLI Y，ROSS C，CASADEI D，et al.Demagnetizations diagnosis for permanent magnet synchronous motors based on advanced wavelet analysis［C］//International Conference on Electrical Machines(ICEM)，Sept 2－5，2012，Marseille，France，2012，2397－2403.

［10］文传博，齐亮.永磁同步电机磁链信息在线监测的新方法［J］.电力系统及其自动化学报，2010，22(2):22－26.

WEN Chuanbo，QI Liang.On-line detection method of magnet flux linkage for permanent magnet synchronous motor［J］.Proceedings of the CSU-EPSA，2010，22(2):22－26.

［11］LU Xiaomin，K.L.V.Iyer，K.Mukherjee，et al.Study and detection of demagnetization in line start permanent magnet synchronous machines using artificial neural network［C］//15th International Conference on Electrical Machines and Systems(ICEMS)，Oct 21－24，2012，Sapporo，Japan，2012，1－6.

［12］ZHANG K，JIANG B，SHI P.Observer-based fault estimation and accomodation for dynamic systems［M］.Springer Heidelberg New York Dordrecht London，2013.

［13］李永东.交流电机数字控制系统.2版［M］.北京:机械工业出版社，2012:337－339.

［14］SPURGEON S K.Sliding mode observers:a survey［J］.International Journal of Systems Science，2008，39(8):751－764.