改进的随机共振和EMD混合模型用于转子早期故障检测

张海如， 王国富， 张法全， 叶金才

(1.西安电子科技大学电子工程学院，陕西西安 710071;2.桂林电子科技大学信息与通信学院，广西桂林 541004)

0 引言

旋转机械作为重要机械结构，已经在石化、电力、冶金和航空航天等国民经济和国防事业的多个领域得到了广泛应用，并且正朝着高速化发展。但由于机械部件润滑不良、防尘防潮不严密、摩擦不均匀、使用寿命等多种因素，容易导致运行的设备发生各种机械故障，而且故障初期征兆难以察觉，经常是出现机器高温、跳动幅度大、异响等破坏性警示时，才发现故障，这往往会带来巨大的生命和财产损失。因此，转子早期故障检测得到了国内外相关领域专家和学者的广泛关注和研究［1－7］。高速旋转机械转子早期故障信号非常微弱，且具有复杂的非线性和非平稳随机性，这造成基于线性平稳理论发展而来的传统微弱周期信号检测技术难以适用。为了实现转子早期故障检测，能处理非线性和非平稳信号且具有良好时频分析特性的小波变换和经验模态分解(empirical code decomposition，EMD)得到了一定的研究，并且取得了一定的成果，人们分别提出了改进的谐波小波方法［8］、粒子群优化最小二乘小波支持向量机方法［9］、双树复小波域隐Markov树模型降噪方法［10］，这些改进的小波变换方法在旋转机械转子早期故障检测中起到了一定的作用，但是小波变换只有选择了合适的小波基函数才能发挥作用，而且一旦选择了基函数，在整个检测过程中都不能改变，这会存在较大的漏警概率;还有人提出EMD分解与敏感度评估算法相结合的方法［11］和EMD分解与广义维数相结合的方法［12］用于旋转机械故障检测，这些改进EMD分解具有一定的应用价值，但是在EMD分解时仍存在端点效应，且在强噪声背景下进行EMD分解时，分解得到的各个基本模式分量(intrinsic mode functions，IMF)存在严重的频率混跌失真，这会对转子早期故障检测造成巨大影响，为了使漏警率为零，这些方法会带来较大的虚警率。此外，由于随机共振系统具有能在极限信噪比下检测微弱周期信号的功能，人们提出了多种改进的随机共振系统用于早期机械故障检测［13－15］，但是由于工业现场各种随机噪声的存在，可能导致随机共振系统发生虚警，将噪声干扰误检测为故障信号。

针对现有旋转机械转子早期故障检测方法的不足，本文建立了尺度变换随机共振降噪下的EMD分解模型，该模型充分利用了尺度变换随机共振在全频段内自适应检测微弱周期信号所含频率的能力和EMD分解对多频混跌信号自适应分解的能力，并通过对EMD分解出的各个IMF进行处理，以还原出共振频率对应信号的幅度值，以其幅值大小判断随机共振系统是否发生虚警，从而保证该模型对转子早期故障检测的准确性。

1 混合模型用于转子早期故障检测

1.1 尺度变换随机共振系统

随机共振系统能在极低的信噪比下提取微弱周期信号，但只适用于小参数信号，为了克服这一不足，已提出了尺度变换随机共振降噪的方法［15］，该方法能在全频段范围内自适应地检测到待测信号所含频率分量，其实现步骤。

1)将含噪信号sn(t)输入以非线性朗之万方程构造的随机共振系统。

随机共振系统方程为

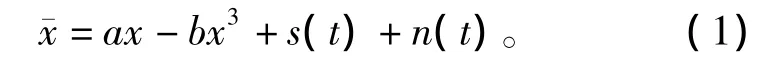
式中:s(t)为待测信号;n(t)为待测信号所含噪声成分;x为输出信号;a、b为系统的非线性参数，其值根据实际情况可进行调整。

2)步骤1)中若检测到共振频率fi，则将该信息保存并从原含噪信号sn(t)中滤除该分量，得到新的含噪信号sn(t)，重新执行步骤1);否则，执行步骤3)。

3)对当前含噪信号sn(t)进行尺度变换，将其频率值缩小10倍后，重新执行步骤1)，重复该过程，直到频率值的总的缩小倍数是待测目标信号预计最大频率值的100倍时，执行步骤4)。

4)将检测到所有频率分量fi进行反尺度变换，还原出实际频率值。

1.2 EMD分解原理

EMD分解的基本原理是将原始输入信号分解成一系列IMF的组合，然后针对具体的应用环境进行后续的分析处理，以提取待测信号的本征信息。能进行EMD分解的信号必须具备两个条件，分别是:待测信号的数据序列极值点和过零点的个数最多相差一个;局部极大值和极小值拟合的上下包络线要局部关于坐标轴对称。通过EMD分解能将待测信号的数据序列x(t)分解成式(2)，分解的详细步骤可参考文献［16］。

式中:ci为n个IMF;rn为残余分量。该分解过程只依赖于原始信号序列的固有特征，是靠经验知识自适应完成的，而且分解提取到的各个IMF具有平稳性，可用于对原始信号序列进行后续处理。EMD分解的过程可以看成是一个带通滤波的过程，每个ci代表一个频段的信号分量，但是由于实测信号受到各种噪声干扰，各个IMF会发生频率混跌失真，给后续信号处理带来麻烦。因此，对信号进行分解前进行降噪处理是很必要的。

1.3 转子早期故障检测算法

尺度变换随机共振降噪下的EMD分解用于旋转机械转子早期故障检测，其实现步骤如下，图1为其实现流程。

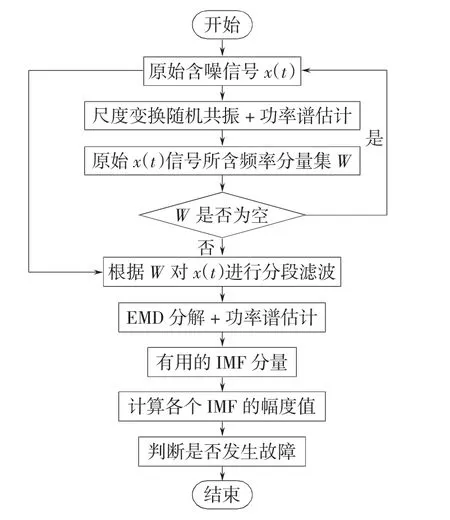
图1 混合模型的流程Fig.1 Flow diagram of the conjoint model

1)将转子的原始含噪信号x(t)通入尺度变换随机共振系统，提取出x(t)所含的各个频率分量，并将这些频率分量保存在数据集合W={fi|i=1，2，…，n}中。重复执行该过程，直到W为非空集合时，执行步骤2)。

2)根据数据集合中所含的各个频率分量，W采用带通滤波器对原始信号x(t)进行分段滤波处理，得到新的仅保留目标频率分量的信号x'(t)。

3)对x'(t)进行EMD分解，得到其所含的各个IMF，并通过对各个IMF进行功率谱估计找到目标频率值对应的IMF。由于x'(t)是降噪后的信号，此时的各个IMF频率单一，不存在频率混跌失真。

4)对各个有用的IMF进行处理，得到其对应的幅度特征。

求取各个IMF的幅度特征的步骤为:a)为了去除EMD分解的边界效应的影响，对ci两端各去除其对应频率的两个周期的信号值，用其中间区域c'i求取该频率信号对应的幅度值;b)对c'i取绝对值得到c″i，求取c″i的各个局部极大值，并将其存入数据集合Mi={Aj|j=1，2，…，n}中;3)求取Mi平均值Ai，Ai作为ci的幅度值。

5)根据ci的幅度值Ai的大小验证尺度变换随机共振系统是否发生虚警，以使整套系统达到零虚警率。

在具体的应用中，首先采集多组已知发生故障的旋转机械的振动信号，并统计出其最小值θmin，为了减小虚警事故的发生，早期故障的阈值设为θmin/2。

2 仿真实验研究

已知强噪声背景下的含噪信号sn(t)=s(t)+n(t)，式中n(t)为强度D=0.5的高斯白噪声，目标信号s(t)=A1sin(ϖ1t)+A2sin(ϖ2t)，其中，A1=A2=0.005 A，ϖ1=10 Hz，ϖ2=30 Hz。将sn(t)通入如图1所示的尺度变换随机共振降噪下的EMD分解系统，以验证该系统的性能，原始的含噪信号sn(t)如图2所示。

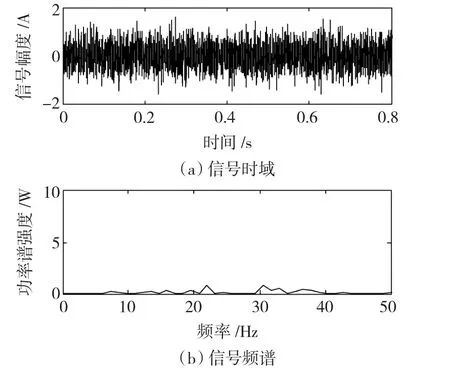
图2 原始含噪信号Fig.2 The original signal with noise

1)将sn(t)通入尺度变换随机共振系统，只有当将sn(t)的频域压缩1 000倍时，系统才会发生共振，共振频率分别为0.01 Hz和0.03 Hz，所以判定原始含噪信号只含有10 Hz和30 Hz的频率分量。共振时输入随机共振系统的信号如图3所示，系统输出信号如图4所示。

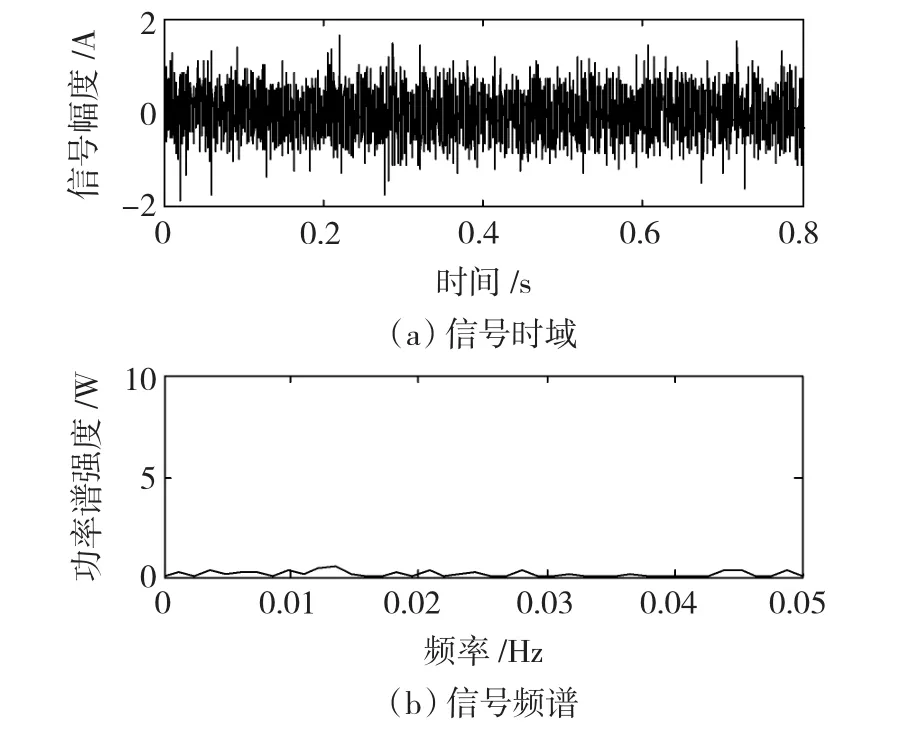
图3 共振时随机共振系统的输入信号Fig.3 Input power spectrum of the bistable system at resonance frequency

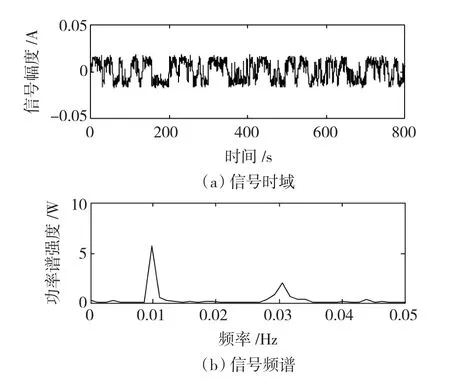
图4 共振时随机共振系统的输出信号Fig.4 Output power spectrum of the bistable system at resonance frequency

2)采用带通滤波器对原始含噪信号sn(t)进行分段滤波处理，得到新的仅保留10 Hz和30 Hz频率分量的信号s'n(t)，信号s'n(t)的特性如图5所示。

3)对s'n(t)进行EMD分解，所得各个IMF，如图6所示。根据对图6中各个IMF进行功率谱估计可知，IMF中c1和c2分别对应原始信号的30 Hz和10 Hz的频率分量，IMF中c3和c4是由于边界效应带来的负效应，但其十分微弱，对原始信号的还原影响甚微。从时域看，IMF中c1和c2的信号波形比较平稳，失真不严重。同时，由于已经对输入信号做了

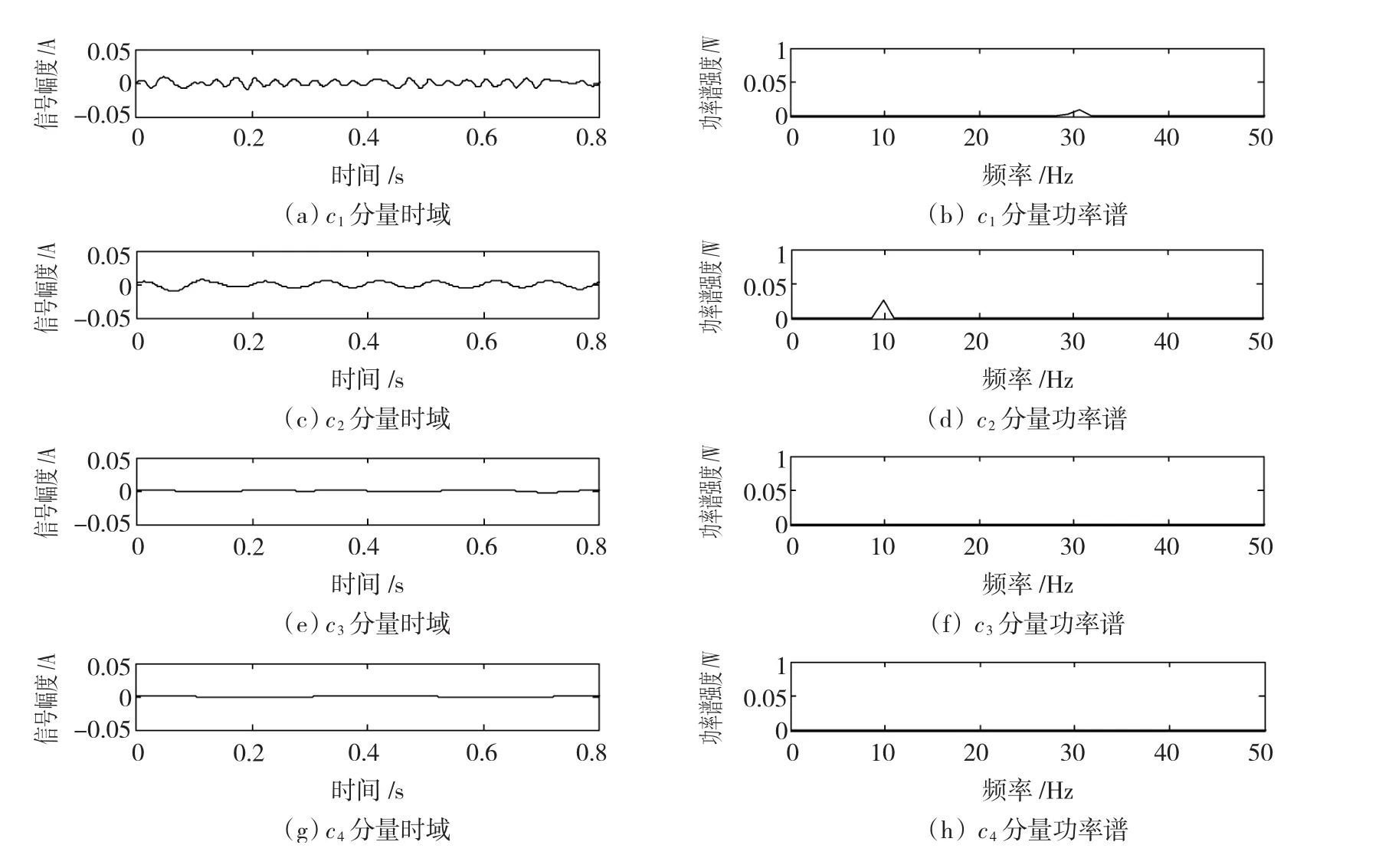
图6 含噪信号降噪后的EMD分解图Fig.6 Effect drawing of the de-noised signal processed by EMD system

降噪处理，使得分解出的IMF数目较少。

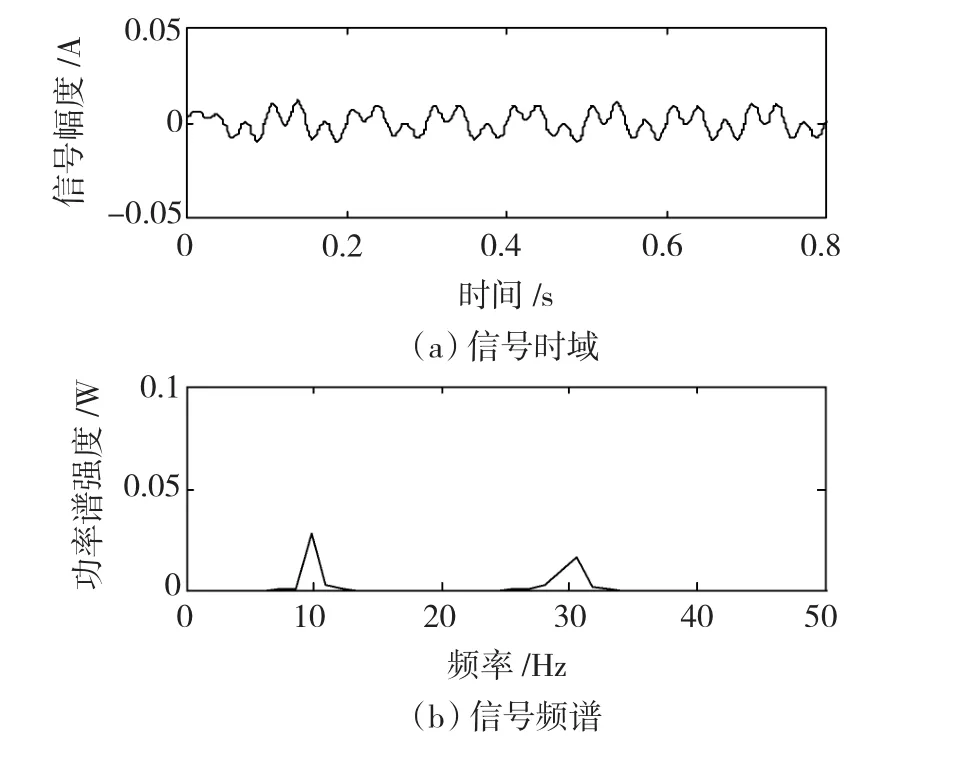
图5 对原始含噪信号进行分段滤波后的信号Fig.5 Effect drawing of the de-noised signal processed by band-pass filter

4)求待测信号30 Hz和10 Hz频率分量所应的幅度值。为了消除边界效应对EMD分解质量的影响，对图6中c1信号两端各去除0.066 s的信号值得到c'1，c2信号两端各去除0.2 s的信号值得到c'2;分别对c'1和c'2取绝对值得到c″1和c″2，分别求取c″1和c″2的局部极大值，并将其存入集合M1和M2中;分别求取集合M1和M2中数据的平均值A1=0.005 2和A2=0.005 8，A1和A2分别为c1分量和c2分量的幅度值，与真实值较好地吻合。

3 实测数据实验

旋转机械的转子绝大部分应用于高转速、高载荷环境中，这容易使轴承表面发生不均匀的磨损、腐蚀、不均匀结垢，造成机械故障。尤其是在故障的早期阶段，在复杂的强噪声背景中，故障信号相当微弱，很难检测到故障的存在，到故障信号变得明显后，即使检测到故障信号的存在，也不可避免的要带来较大的损失。图7为现场采集到的某A型矿用鼓风机转子振动加速度的时间序列信号sA(t)的时域和其对应的频谱，其转速为1 457.61 r/min，从图中不能分析出是否含有故障信息。将该信号通入尺度变换随机共振系统，当该信号的频域压缩1 000倍时，输出信号如图8所示，则检测到该信号中含有49 Hz的频率分量，该频率为转子转速为24.3 Hz的2倍频信号，推断可能发生转子不平衡故障。

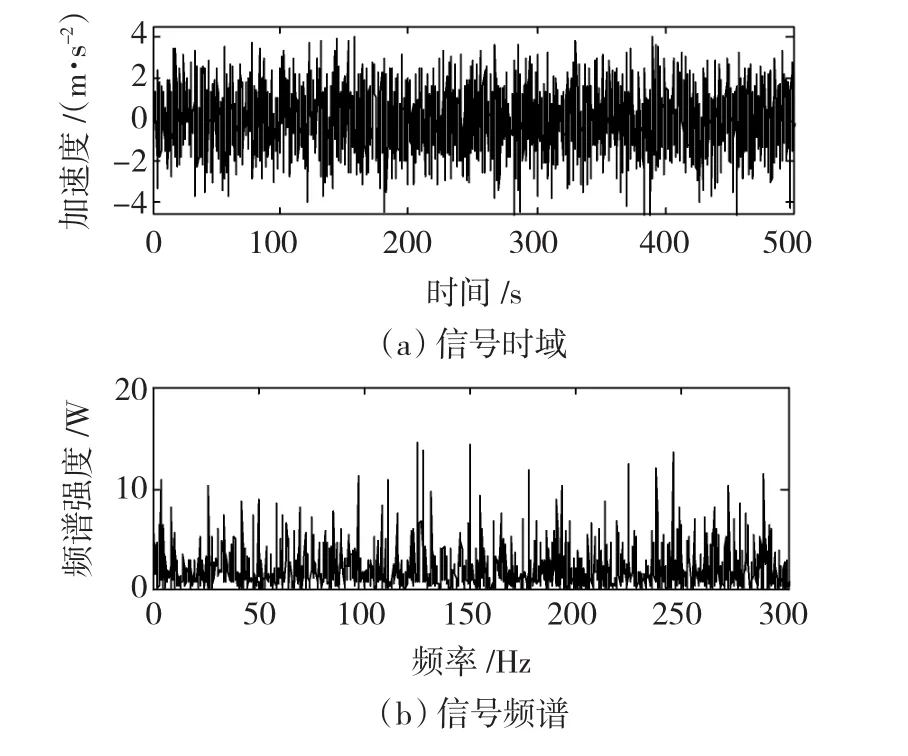
图7 A型矿用鼓风机转子振动加速度信号Fig.7 The vibration acceleration signal of a type A blower’s rotor

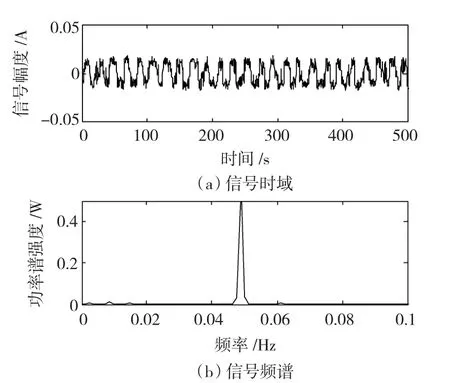
图80 .049 Hz频率分量共振Fig.80 .049 Hz resonance

将原始含噪信号通入中心频率为48 Hz、带宽为4 Hz的带通滤波器，将滤波后的信号进行EMD分解，检测到目标频率信号的幅值为0.000 8 V，图9为信号sA(t)的EMD分解所得曲线。断定该信号幅值微弱，为噪声扰动造成的假异常，经实际检验，转子装配合格，主轴完好无损。

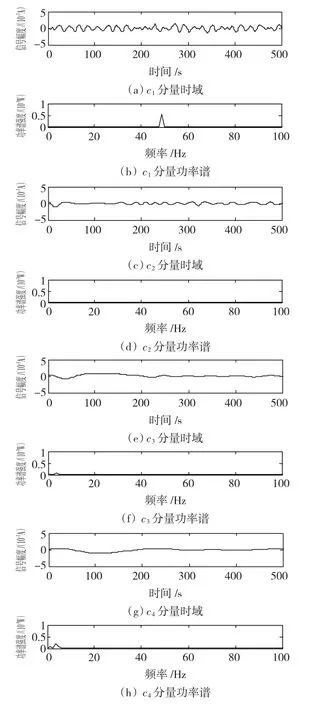
图9 信号sA(t)的EMD分解所得曲线Fig.9 De-noised signal sA(t)processed by EMD system

图10为现场采集到的某B型矿用鼓风机转子振动加速度的时间序列信号sB(t)和其对应的频谱，其转速为984.7 r/min，从图中不能分析出是否含有故障信息。将该信号通入尺度变换随机共振系统，当该信号的频域压缩1 000倍时，输出信号如图11～图13所示，则检测到该信号中含有33 Hz、50 Hz和68 Hz的频率分量，该频率为转子转速为16.4 Hz的2倍频、3倍频和4倍频信号，推断可能发生转子不平衡故障，将原始含噪信号通入中心频率分别为33 Hz、49 Hz和67 Hz，带宽为4 Hz的带通滤波器，将滤波后的信号进行EMD分解，检测到目标频率信号的幅值分别为0.028 V、0.02 V和0.015 V。

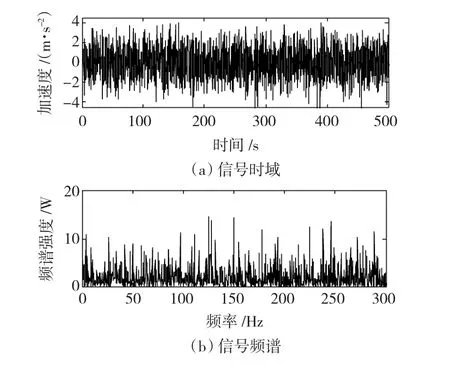
图10 某矿用鼓风机转子振动加速度信号Fig.10 The vibration acceleration signal of a blower’s rotor

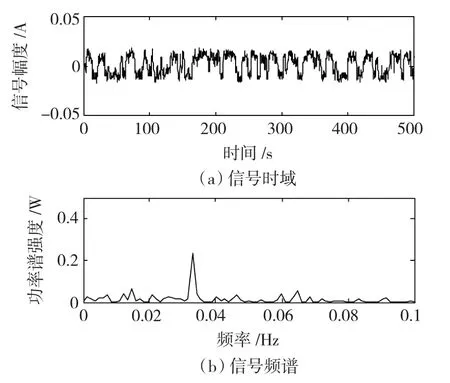
图110 .033 Hz频率分量共振Fig.110 .033 Hz resonance

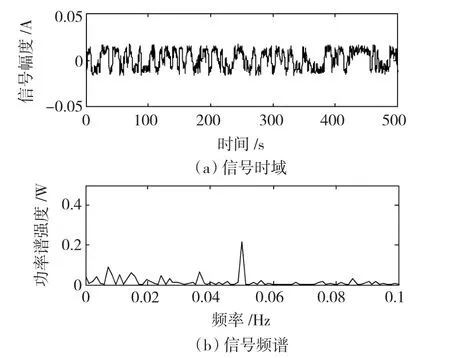
图120 .05 Hz频率分量共振Fig.120 .05 Hz resonance

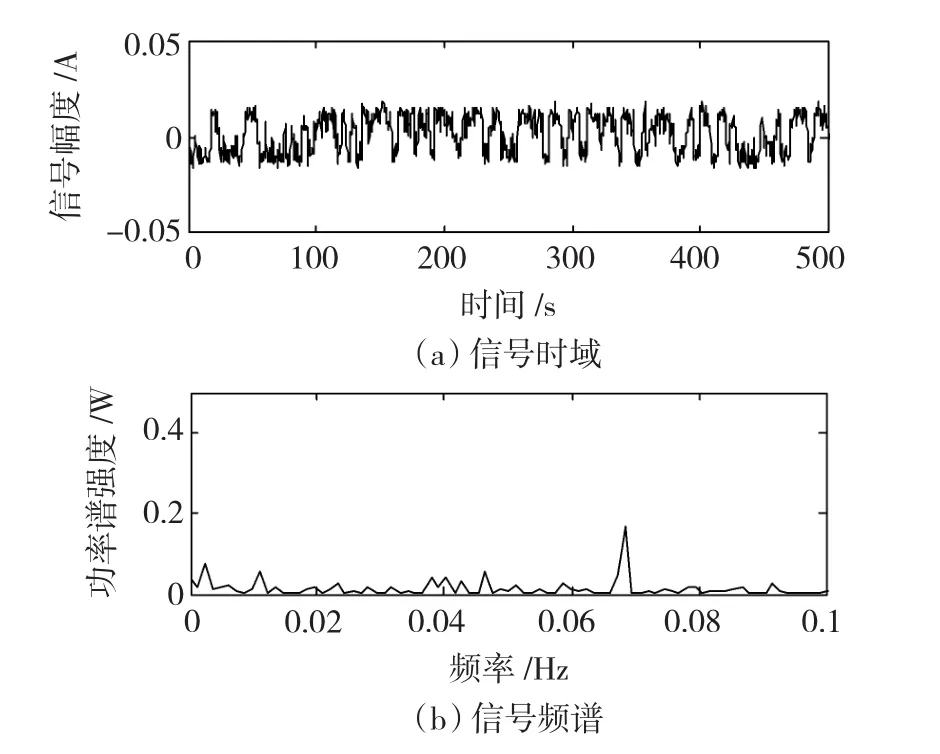
图130 .068 Hz频率分量共振Fig.130 .068 Hz resonance

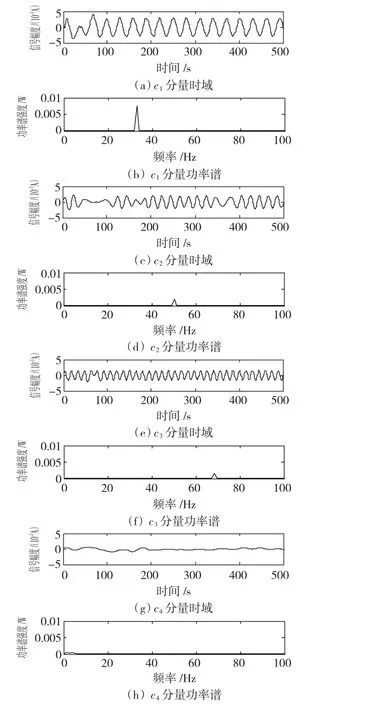
图14 信号sB(t)的EMD分解所得曲线Fig.14 De-noised signal sB(t)processed by EMD system

图14为信号sB(t)的EMD分解所得曲线。断定转子产生了早期不平衡故障，经实际检验，主轴表面已经不均匀结垢，导致转子质心和旋转中心线之间产生了偏心距，转子运转时受到离心力干扰，给主轴带来动载荷，造成转子周期性振动。

4 结语

高载荷快速运转的机械转子很容易发生不平衡故障，若不能在故障发生的早期阶段检测到其存在，往往会给整套设备带来灾难性的后果。常见的微弱信号检测方法在降低噪声的过程中会对信号强度造成一定的压制，这不利于微弱信号的检测。本文提出的尺度变换随机共振降噪下的EMD分解方法，不仅充分利用了尺度变换随机共振系统对全频段微弱信号自适应检测的能力，还引入了具有根据输入信号本征信息就能自适应分解出其对应的各个IMF分量的EMD分解技术。该方法首先将强噪声背景下采集到的旋转机械转子相关信号通入尺度变换随机共振系统，以检测出设备是否含有故障频率分量，并根据这里的检测结果利用带通滤波器对含噪信号进行降噪处理，再对处理后的信号进行EMD分解，进而根据分解得到的各个IMF分量估算出各个频率分量对应的幅度值，根据幅度值大小进一步验证随机共振系统检测到的故障信息是否准确，从而确保对转子早期故障的精确检测。

［1］MEHDI B，ABBAS R B.A new method for detection of rolling bearing faults based on the Local Curve Roughness approach［J］.Polish Maritime Research，2011，18(2):44－50.

［2］DONGSIK G，JAEGU K，YOUNGSU A，et al.Detection of faults in gearboxes using acoustic emission signal［J］.Journal of Mechanical Science and Technology，2011，25(5):1279－1286.

［3］FENG K，JIANG Z，HE W，et al.Rolling element bearing fault detection based on optimal antisymmetric real Laplace wavelet［J］.Measurement，2011，4(9):1582－1591.

［4］李辉，王瀚，白亮，等.改进希尔伯特—黄变换方法提取水轮机动态特征信息［J］.中国电机工程学报，2011，31(2):78－84.

LI Hui，WANG Han，BAI Liang，et al.Dynamic characteristic information extraction of hydroturbine based on improved Hilbert－Huang transform method［J］.Proceedings of the CSEE，2011，31(2):78－84.

［5］孙斌，王艳武，杨立.基于红外测温的异步电机轴承故障诊断［J］.电机与控制学报，2012，16(1):50－55.

SUN Bin，WANG Yanwu，YANG Li.Study of fault diagnosis of induction motor bearing based on infrared inspection［J］.Electric Machines and Control，2012，16(1):50－55.

［6］TIAGO C，BEATRIZ M G，ARMANDO V C，et al.Influence of grease rheology on thrust ball bearings friction torque［J］.Tribology International，2012，46(1):106－113.

［7］LI H，FU L，ZHENG H.Bearing fault diagnosis based on amplitude and phase map of Hermitian wavelet transform［J］.Journal of Mechanical Science and Technology，2011，25(11):2731－2740.

［8］陈果.一种改进的谐波小波及其在转子故障诊断中的应用［J］.机械工程学报，2011，47(1):8－16.

CHEN Guo.An improved harmonic wavelet and its application to rotor faults diagnosis［J］.Journal of Mechanical Engineering，2011，47(1):8－16.

［9］陈法法，汤宝平，董绍江.基于粒子群优化LS－WSVM的旋转机械故障诊断［J］.仪器仪表学报，2011，32(12):2747－2753.

CHEN Fafa，TANG Baoping，DONG Shaojiang.Rotating machinery fault diagnosis based on LS－WSVM with particle swarm optimization［J］.Chinese Journal of Scientific Instrument，2011，32(12):2747－2753.

［10］苏文胜，王奉涛，朱泓，等.双树复小波域隐Markov树模型降噪及在机械故障诊断中的应用［J］.振动与冲击，2011，30(6):47－52.

SU Wensheng，WANG Fengtao，ZHU Hong，et al.Denoising method based on hidden Markov tree model indual tree complex wavelet domain and its application in mechanical fault diagnosis［J］.Journal of Vibration and Shock，2011，30(6):47－52.

［11］雷亚国.基于改进Hilbert－Huang变换的机械故障诊断［J］.机械工程学报，2011，47(5):71－77.

LEI Yaguo.Machinery fault diagnosis based on improved Hilbert－Huang transform［J］.Journal of Mechanical Engineering，2011，47(5):71－77.

［12］郝研，王太勇，万剑，等.基于经验模式分解和广义维数的机械故障诊断［J］.吉林大学学报:工学版，2012，42(2):392－396.

HAO Yan，WANG Taiyong，WAN Jian，et al.Mechanical fault diagnosis based on empirical mode decomposition and generalized dimension［J］.Journal of Jilin University:Engineering and Technology Edition，2012，42(2):392－396.

［13］HE Q，WANG J，LIU Y，et al.Multiscale noise tuning of stochastic resonance for enhanced fault diagnosis in rotating machines［J］.Mechanical Systems and Signal Processing，2012，28:443－457.

［14］WANG J，ZHANG Q，XU G.Genetic stochastic resonance:a new fault diagnosis method to detect weak signals in mechanical systems［J］.Advanced Science Letters，2011，4(6－7):2508－2512.

［15］王国富，张海如，张法全，等.时频压缩随机共振用于转子故障早期检测［J］.电机与控制学报，2011，15(6):38－44.

WANG Guofu，ZHANG Hairu，ZHANG Faquan，et al.Frequency compression of SR for detecting rotor’s incipient fault signal［J］.Electric Machines and Control，2011，15(6):38－44.

［16］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，1998，454(12):903－995.