三相SPWM逆变器的切换模型与稳定性分析

韩璐， 肖建， 邱存勇

(西南交通大学电气工程学院，四川成都 610031)

0 引言

三相逆变器电路因为功率开关器件的存在，具有典型的非线性、多开关模态等特点。传统的三相逆变器分析方法都是从线性系统的角度出发，通过平均化［1－3］、坐标变换或小信号线性化［4－6］等方法得到系统的近似线性化模型，并针对该模型进行稳定性分析与控制。此类方法虽然经典，有很强的理论支持，却由于忽略了系统的某些因素，不能体现出三相逆变器的混杂动态特性，对系统分析有很大的局限性。

近年来提出的切换系统理论［7］可以很好地解决线性化处理为系统分析带来的局限性，更精确地反映系统的动态混杂特性，进而有利于设计更加可靠灵活的控制器，有很好的应用前景。所谓切换系统［7］是指离散事件系统(DES)和连续变量系统(CVS)相混合而形成的统一的动态系统。由于功率开关器件的存在，大部分的电力电子装置都是典型的切换系统。文献［8］基于切换系统理论构建了DC/DC变换器的切换系统模型，并基于该模型提出DC/DC电路的参数辨识方法。文献［9－10］从切换的角度提出了DC/DC变换器的建模与控制新方法。但是上述方法仅限于由两个子系统组成的切换系统，对于更复杂的电力电子电路，随着开关模式的丰富，子系统大大增加，该方法便不再适用。文献［11］针对复杂电路，在切换理论基础上建立了三相变流器的切换系统模型，并引入等时切换系统的稳定性判据进行稳定性分析，该方法对研究普遍的电力电子装置有一定的参考价值。

三相SPWM逆变器属于三相变流器的一种，是典型的周期切换系统。基于文献［12］提出的周期切换系统渐近稳定的充要条件，文献［11］对三相变流器切换过程的稳定性进行了初步分析，但是由于系统模型是在等时周期切换这一特殊情况下建立的，在稳定性分析过程中存在一定的局限性。本文在此基础上进行改进，以周期切换系统理论为基础，从三相SPWM逆变器的建模与稳定性分析两个方面分别进行设计。首先，根据SPWM调制特性，将一个工频周期按三相母线电压大小划分为6个区间，分别得到切换子系统与对应的周期切换规则，即三相SPWM逆变器的周期切换模型。在系统稳定性分析方面，本文通过将切换子系统滞留时间当作不确定参数，将三相SPWM逆变器的切换模型转换为多胞型模型，并利用多胞型模型与周期切换系统的稳定性等价关系实现对三相逆变器切换过程的稳定性判断。为了降低保守性，多胞型模型的稳定性分析中利用参数依赖型Lyapunov函数。

1 三相SPWM逆变器切换动态模型

1.1 子系统模型

图1为三相SPWM逆变器［4］的拓扑结构图，它是基于电压型变流器(VSC)结构的功率逆变电路，其工作原理是通过SPWM(正弦波脉宽调制)技术控制功率开关器件S1～S6的关断，使得输出的电压或电流为标准正弦波，达到逆变电源的要求。因为功率开关器件的存在，三相SPWM逆变器为典型的切换系统。

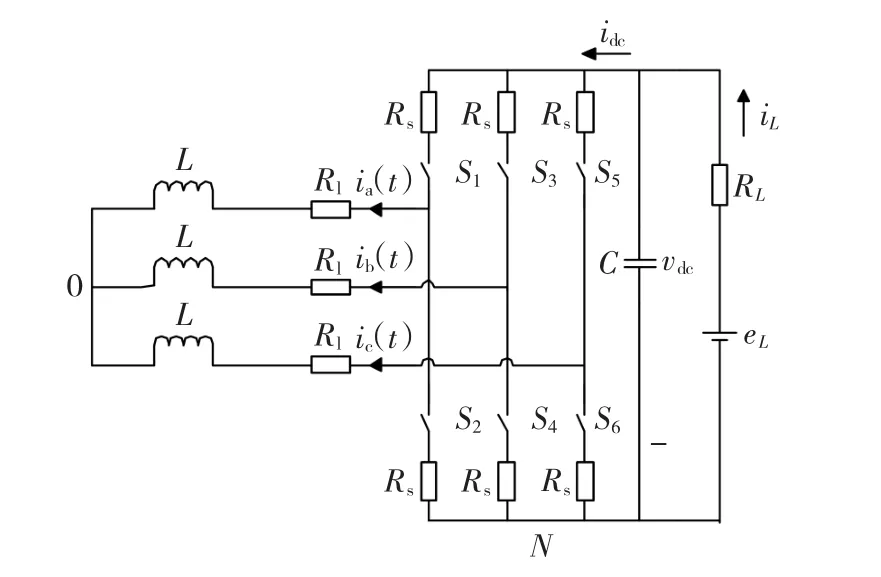
图1 三相SPWM逆变器的拓扑结构图Fig.1 Topology of three-phase SPWM inverter

为分析方便，首先定义单极性二值逻辑开关函数sk为

将三相VSC功率开关管损耗Rs同交流侧负载电阻Rl合并，且令R=Rl+Rs，采用基尔霍夫电压定律建立三相电压型逆变器的a相回路方程为

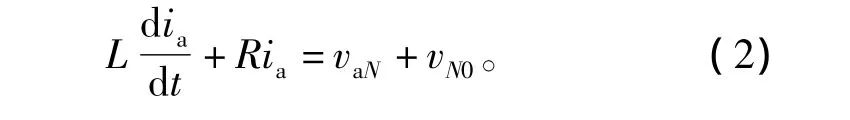
其中vaN=vdcsa。

同理可得b相、c相回路方程为

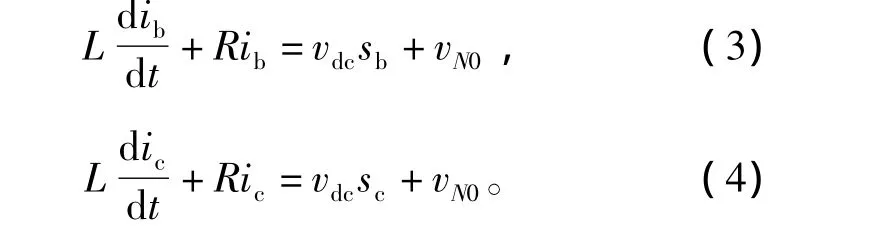
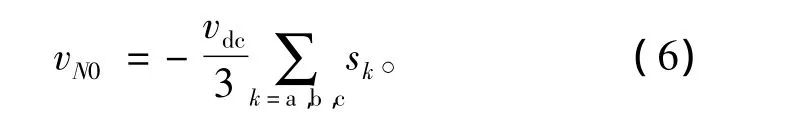
另外，对直流侧电容正极节点处采用基尔霍夫电流定律，得

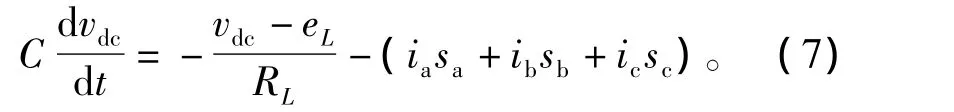
考虑三相对称系统，则

联立式(2)～式(5)，得

令状态变量x=［ia，ib，ic，vdc］T，则采用单极性二值逻辑开关函数描述的三相电压型逆变器的一般状态方程可以表示为

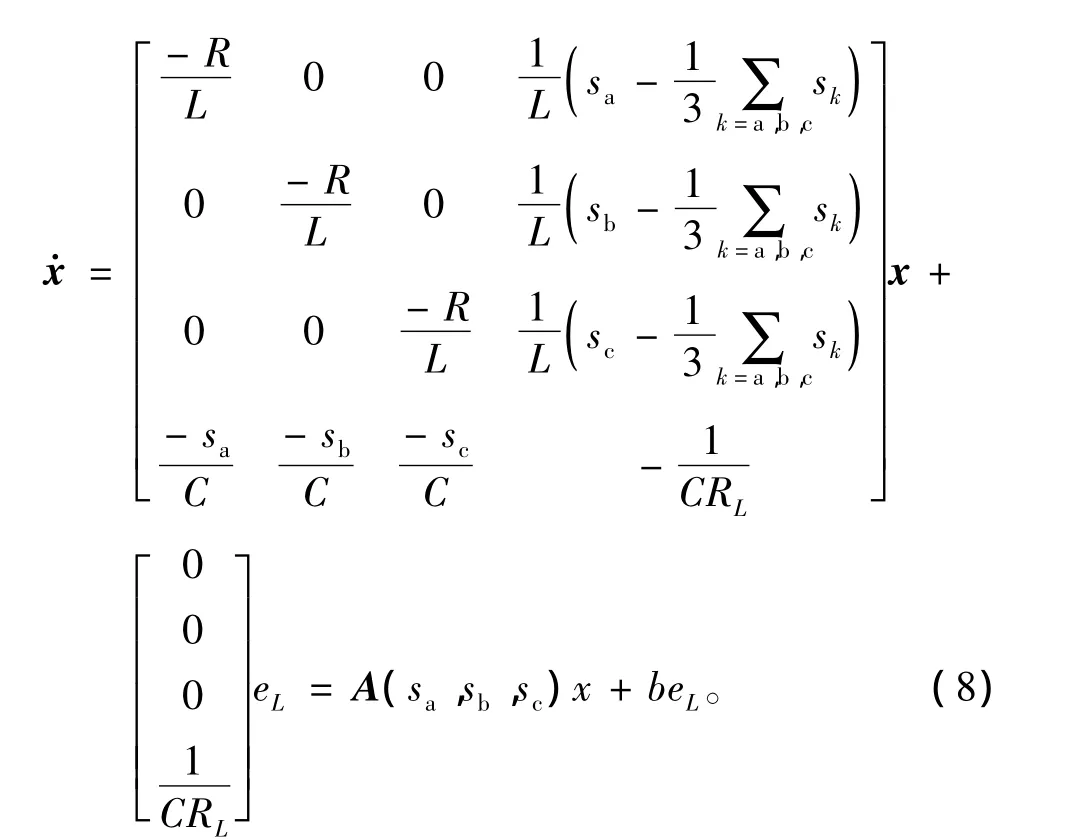
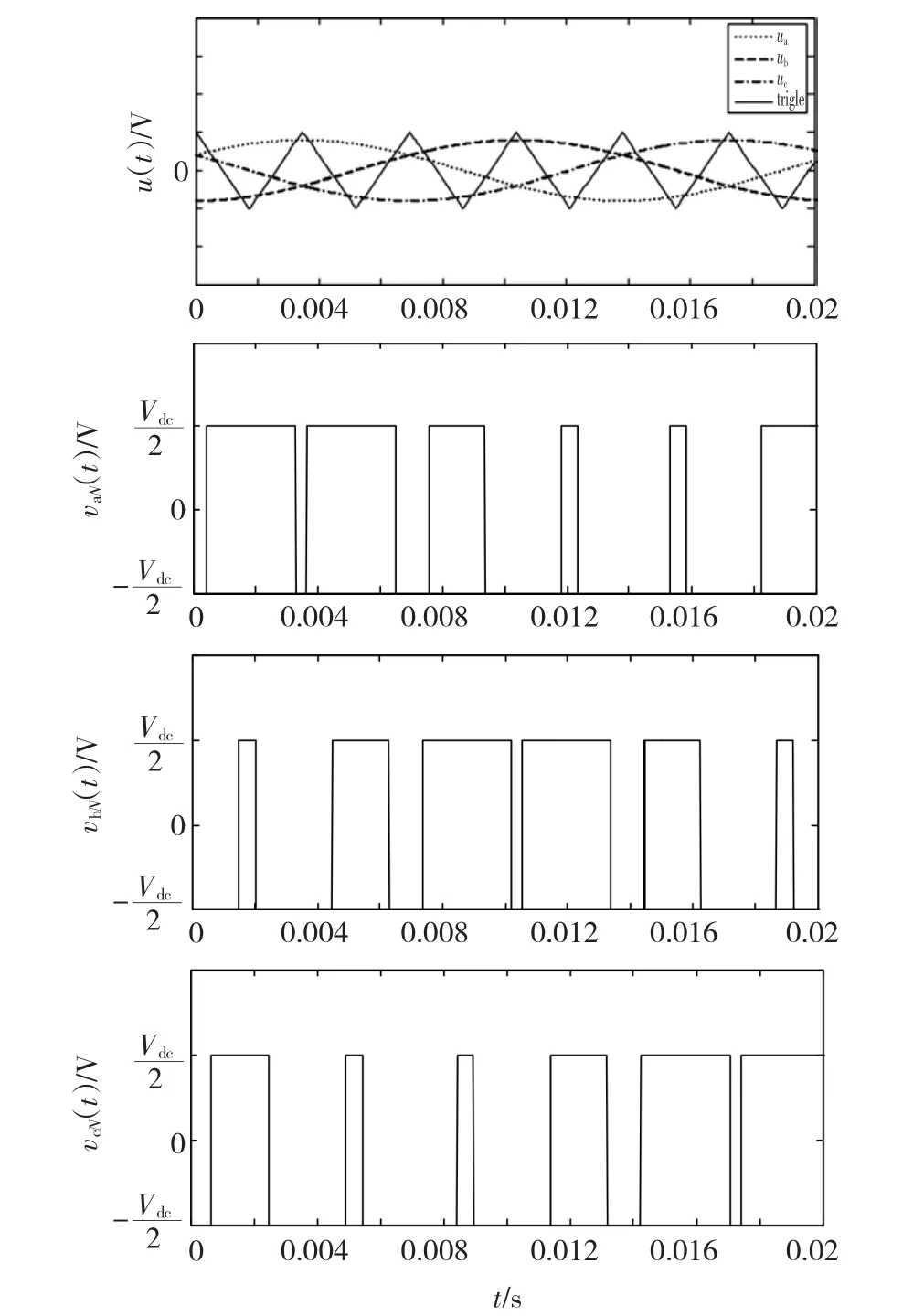
图2 SPWM波形产生原理Fig.2 Schematic diagram of SPWM pulses generation

其中:sa、sb、sc的值不同对应不同的系统矩阵。根据式(1)，sa、sa、sc组成系统的8种开关模态，如表1所示。

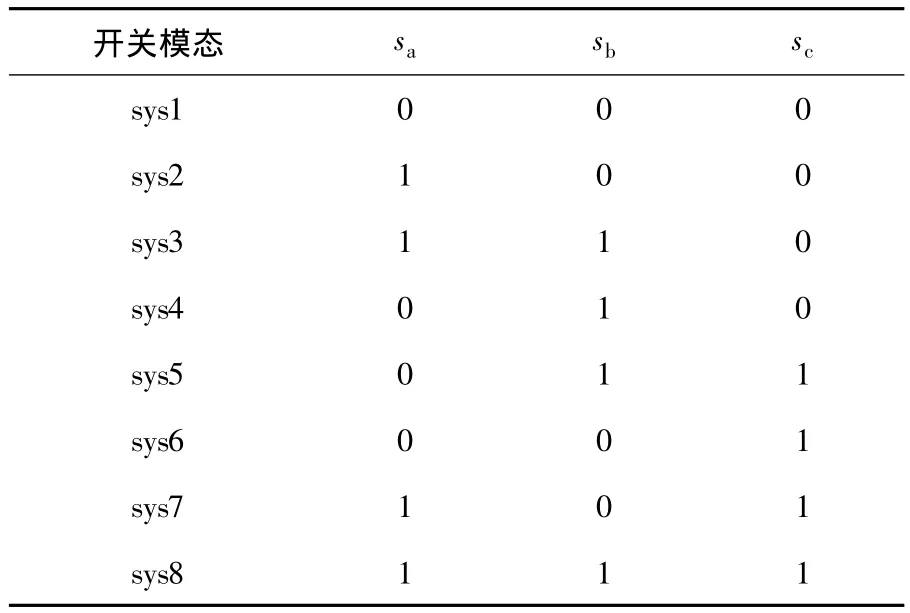
表1 SPWM逆变器的8种开关模态Table 1 Different switching modes of SPWM inverter

SPWM逆变器的开关模态即为系统的切换子系统，将表1中sa、sb、sc的值代入式(8)，可以得到三相电压型逆变器的切换子系统模型

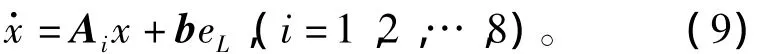
1.2 切换规则

线性切换系统的模型由两部分组成，分别是线性子系统以及切换规则。SPWM控制方式是一种特殊的切换规则，它是对逆变电路开关器件的通断进行控制，使得输出端得到一系列幅值相等而宽度不相等的脉冲，用这些脉冲来代替正弦波或其它需要的波形。SPWM调制原理如图2所示。

文献［11］提出的SPWM逆变器模型中，切换规则被处理为8个子系统依次切换的等时周期切换，这种处理方式存在一定的局限性。根据SPWM调制原理，SPWM逆变器的切换规则应该是受三相母线电压大小影响的周期切换，切换周期为工频周期。

为了用数学方法归纳SPWM这种特殊的切换规则，将一个工频周期内的调制过程按三相正弦调制电压的交点从左向右分为ua＞uc＞ub，ua＞ub＞uc，ub＞ua＞uc，ub＞uc＞ua，uc＞ub＞ua和uc＞ua＞ub六个区间，由于三相对称性，每个区间的时间取值为T/6，记为Ts。下面以ua＞uc＞ub为例详细介绍系统的切换规则，为了分析方便，假设SPWM调制过程中三角载波周期也为T 。

当母线电压满足ua＞uc＞ub时，三相共载波SPWM控制方式如图3所示。

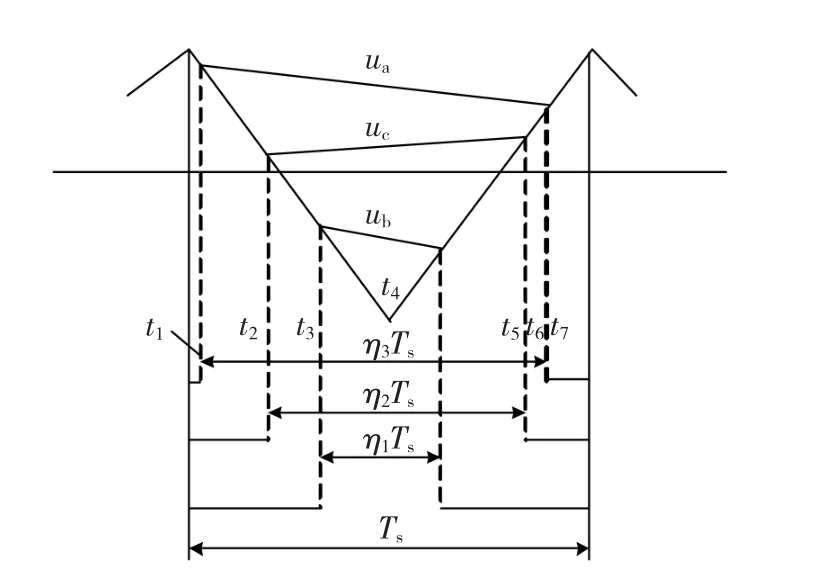
图3 三相共载波PWM调制原理Fig.3 Three-phase PWM pulses generation with common carrier wave

这种控制方式是将三相作为一个整体，在同一个周期Ts中同时对a，b，c三相进行调制。图中通过SPWM调制过程产生了7个时间区域，对应着不同的子系统模态，三相调制电压对应不同的占空比，分别是η1，η2和η3。因为7种子系统模态中有些模态存在逆变过程的重复，可以看作冗余模态，所以对图3的脉宽重新排列顺序得到三相共载波SPWM波形，如图4所示。

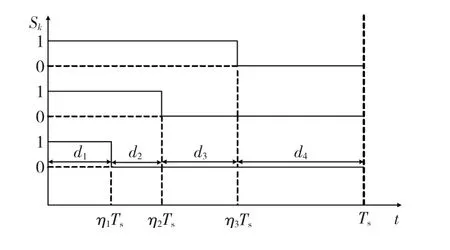
图4 重排后的SPWM波形Fig.4 Three-phase SPWM pulses after rearrangement

由图4可以看出，在同一开关周期Ts中，经过SPWM调制只产生四个时间区间d1，d2，d3和d4。这4个时间区间分别对应表1中的子系统sys1，sys2，sys7，sys8，将相应sa、sb、sc的值代入式(8)，可以得到子系统矩阵A1，A2，A7，A8。其余五个区间的分析类似，不再重复。值得指出，由于三相对称性和区间选取的平均原则，每个区间对应子系统的滞留时间是相等的。从以上的分析得出三相SPWM逆变器的周期切换规则如图5所示。

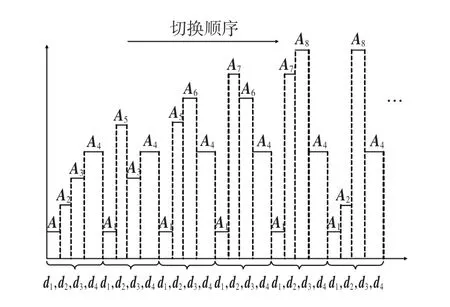
图5 三相SPWM逆变器的周期切换规则Fig.5 Periodic switching rules of three-phase SPWM inverter

由于SPWM调制原理遵循脉宽调制原则，图5中每个子系统的滞留时间d1，d2，d3，d4可理解为正弦波幅值对应的等效脉宽，即遵循正弦波变化规律。从这一角度可以得到子系统滞留时间d1，d2，d3，d4的实际数值。

值得注意的是，三角波载波周期不同，所得到的切换规则是不同的，对应的子系统滞留时间也是不同的，但是均可通过以上方法归纳出系统切换规则。

2 三相SPWM逆变器的稳定性分析

三相SPWM逆变器为典型的线性仿射周期切换系统［11］。考虑到其不同开关组合对应的子系统模型(9)为线性时不变的，且仿射项beL为恒定常数，不受切换过程的影响，三相SPWM逆变器的稳定性分析可以简化为对线性自治周期切换系统=Aix的稳定性判断，进而可以利用下述引理。

引理1［12］切换系统=Aix，i=1，2，…，m通过周期切换规则后渐近稳定的充要条件是系统αiAix渐近稳定，其中αi是正整数且满足τi=αiτ，i=1，2，…，m，τi为周期切换下的子系统滞留时间，τ为等时周期切换下的子系统滞留时间。

文献［11］曾引用过该周期切换系统的稳定性判据对三相变流器进行稳定性分析，但是整个分析过程均建立在等时周期切换这一特殊情况下，即假设 αi=1，i=1，2，…，m，有一定的局限性。在此基础上做以改进，通过将切换子系统滞留时间作为不确定参数，将三相SPWM逆变器的切换模型转换成多胞型模型［13］，进而利用引理1实现对三相逆变器切换过程的稳定性判断。为了降低保守性，多胞型模型的稳定性分析中利用参数依赖型Lyapunov函数，具体步骤如下。

由于子系统滞留时间随着三角波载波周期的不同而变化，逆变器各子系统的滞留时间可以看作不确定参数(这些参数均可测量)，则SPWM逆变器的自治切换动态模型转换成参数不确定多胞型模型为

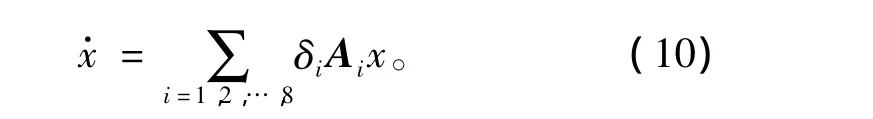
之后利用鲁棒控制的相关理论对系统(10)进行稳定性分析。值得指出的是，对于这种参数不确定系统的鲁棒控制理论早已成熟，最常用的二次稳定性判据［13］为公共Lyapunov判据，它要求有一个对所有的不确定参数都适用的Lyapunov矩阵，所以在简单易设计的同时存在很大的保守性。为了避免该保守性，本文采用参数依赖的Lyapunov矩阵［13－16］对三相SPWM逆变器的多胞模型进行稳定性分析。参数依赖型Lyapunov稳定性判据如定义1所示。

定义1称具有式(10)系统矩阵的多胞模型为二次稳定［13］的，当且仅当存在一组对称矩阵Pi，i=1，2，…，8，使得对所有的不确定参数 δ∈Δ，

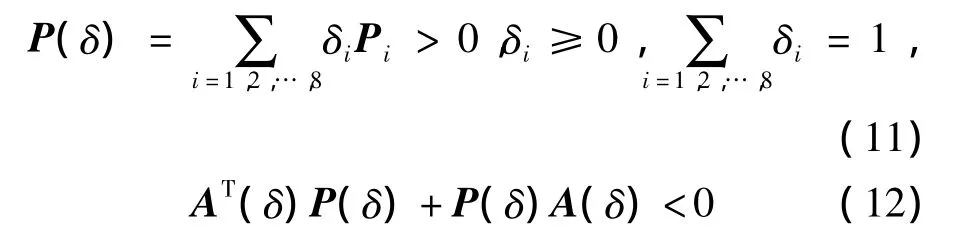
成立。其中矩阵P(δ)是不确定参数δi的一个多胞函数。

该定义中提出的线性矩阵不等式判据，可以利用Matlab中的鲁棒控制工具箱LMI来求解。LMI工具箱提供了检验由多胞型模型所描述的不确定系统二次稳定性的函数pdlstab［13］，其一般表达式为

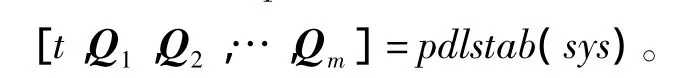
其中，sys为多胞型模型的系统矩阵，且函数输出为参数依赖矩阵

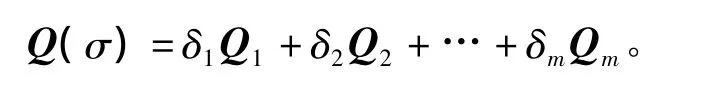
该函数指出，如果t＜0，则所考虑的系统为多胞二次稳定的，且V(x，δ)=xTQ－1(δ)x定义了一个参数依赖的Lyapunov函数。

二次稳定的系统必然渐近稳定。利用参数依赖型Lyapunov稳定性判据和LMI工具箱函数pdlstab可以很容易地从子系统矩阵A1～A8的数值中判断出三相SPWM逆变器的多胞不确定系统模型(10)为渐近稳定的，进而根据引理1得到经周期切换序列下的原切换系统(9)稳定。

3 数字仿真

为了验证本文构造的逆变器模型以及稳定性分析方法的正确性，本节在Matlab软件环境下进行了系统仿真。假设R/L=2 500，1/L=125，1/C=100，1/CRL=5，eL=400 V，切换周期T=0.02 s，载波频率fs=300 Hz，子系统滞留时间分别为d1=0.000 65 s，d2=0.001 16 s，d3=0.001 16 s，d4=0.000 36 s。令系统初始状态x0=(20，20，20，300)T，则三相逆变器切换子系统(9)通过图5周期切换规则后的系统状态轨迹如图6所示。

系统的状态轨迹体现了一定的切换特征。由图6可知，在8个子系统以工频为周期做周期切换的情况下，系统状态各分量随时间的变化曲线是连续的且随时间的增大始终收敛于有限区域内。该仿真波形体现了切换系统的稳定性，与之前的分析结果共同证实了周期切换模型与系统等效多胞型模型的稳定等价性，进而说明了本文关于三相SPWM逆变器的稳定性分析方法是正确的。

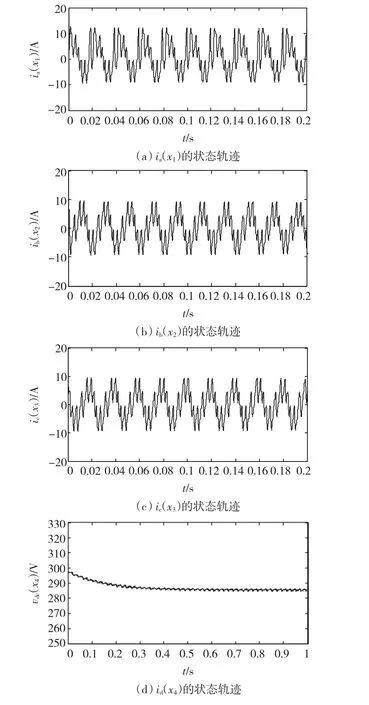
图6 周期切换规则下逆变器的状态轨迹Fig.6 State movement track of inverter under periodic switching series

同时，为了体现本文建立的逆变器切换模型较传统的线性近似化模型的优越性，分别对两种模型下输出的a相电压波形进行比较分析，如图7所示。

由图7的对比波形可以看出，在相同载波频率下，所建立的逆变器切换模型输出的a相电压波形平滑均匀，抗干扰能力强，较传统的小信号线性化模型输出的电压波形更接近于指令正弦波，更满足三相SPWM逆变器的工作要求。

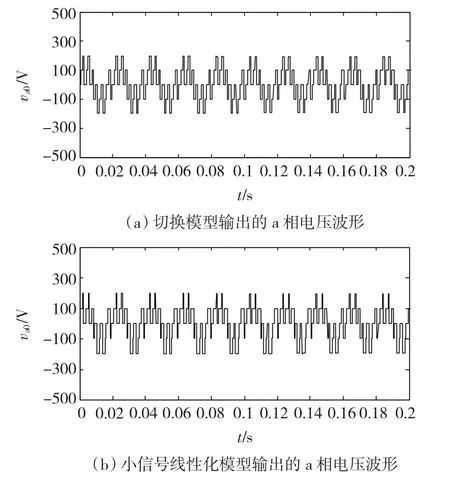
图7 不同模型下的a相输出电压波形Fig.7 Output a-phase voltage waveforms of different models

以上仿真结果只给出了三相SPWM逆变器切换模型输出的a相稳态电压波形。为了更全面地体现切换系统模型的抗干扰能力，本节还给出了扰动情况下a相输出电压的特性分析。假设在t=0.1 s时刻，直流电压eL由400 V突变到800 V，a相输出电压的暂态波形如图8所示。

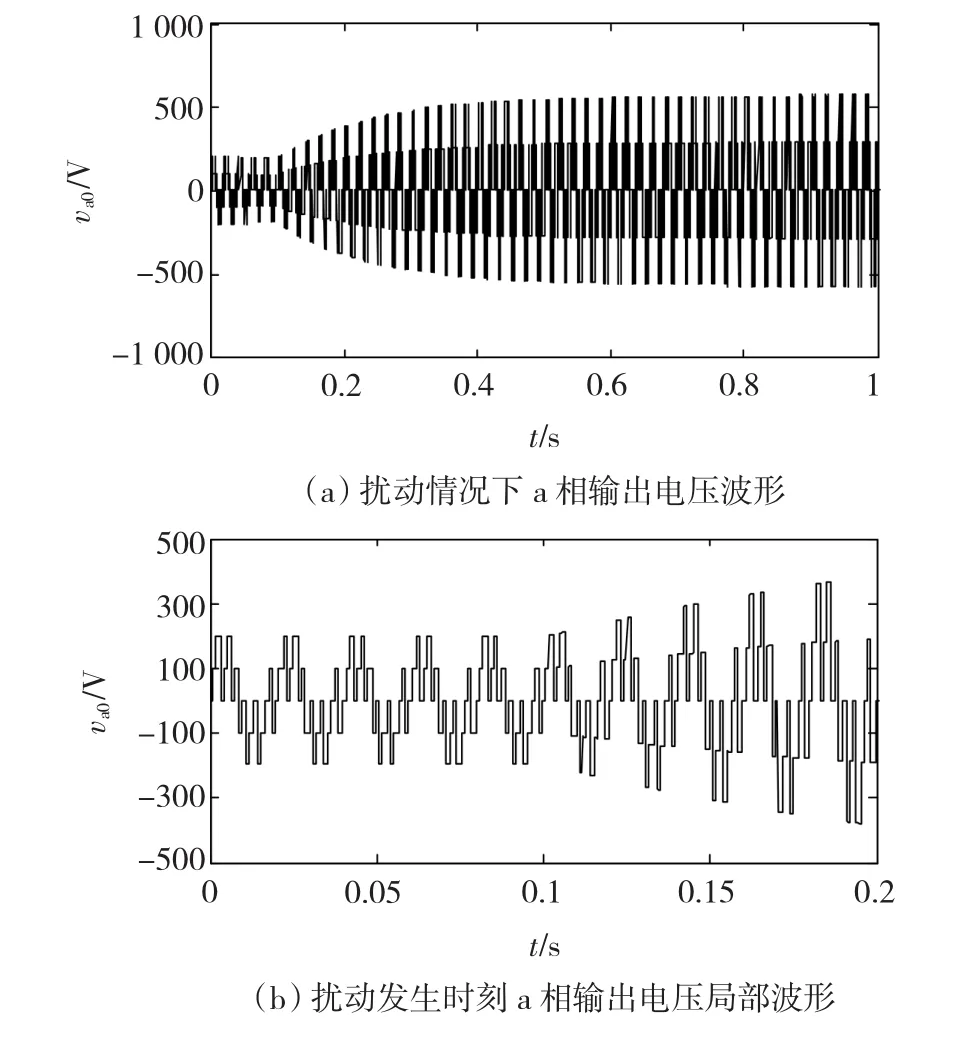
图8 扰动情况下a相输出电压波形Fig.8 Output a-phase voltage waveform under disturbance

图8清晰地呈现出在扰动产生瞬间，三相SPWM逆变器切换模型输出的a相暂态电压波形平滑过渡，且随着时间的推移逐渐稳定在新的指令值上。值得注意的是，载波频率越高，输出的电压波形越接近正弦波。本节考虑仿真时效性采用了较低的载波频率，工程中只要适当提高载波频率，该切换模型可以达到更好的效果。

4 结论

由SPWM调制原理可知，三相逆变器是典型的周期切换系统。本文以周期切换系统理论为基础，从三相SPWM逆变器的建模与稳定性分析两个方面分别进行设计。在系统建模方面，本文将一个工频周期按三相母线电压大小划分为6个区间，分别得到切换子系统与切换规则，即三相SPWM逆变器的周期切换模型。这样得到的切换规则较文献［11］提出的8个子系统依次切换的等时切换规则更符合实际系统的动态需要。在系统稳定性分析方面，本文在文献［11］的关于等时周期切换方法的基础上加以改进，通过将切换子系统滞留时间作为不确定参数，利用多胞型模型的稳定性判定方法来判断三相SPWM切换系统的稳定性。为了避免保守性，在多胞型模型的稳定性分析中采用了参数依赖型Lyapunov函数。最后，在Matlab软件环境下的仿真结果验证了本文关于三相逆变器切换模型以及稳定性分析方法的正确性。值得指出的是，本文提出的基于切换系统理论的系统建模与稳定性分析方法可以推广到具有周期切换特性的其他PWM变换器的研究中，有一定的普遍意义。

［1］Middlebrook R D.Small-signal modeling of pulse-width modulated switched-mode power converters［J］.Proceedings of the IEEE，1988，76(4):343－354.

［2］王立建，王明渝，刘洋.一种新型的电压源逆变器并联控制策略［J］.电力系统保护与控制，2012，40(2):51－55.

WANG Lijian，WANG Mingyu，LIU Yang.A novel control strategy for parallel operation of voltage source inverter［J］.Power System Protection and Control，2012，40(2):51－55.

［3］董锋斌，皇金锋.一种三相SPWM逆变器的建模和控制方法［J］.电机与控制学报，2010，14(8):87－92.

DONG Fengbin，HUANG Jinfeng，ZHONG Yanru.A modeling and controlling approach of three-phase SPWM inverter［J］.Electric Machines and Control，2010，14(8):87－92.

［4］张崇巍，张兴，PWM整流器及其控制［M］.北京:机械工业出版社，2002.

［5］Ye Y，Kazerani M，Quintana V H.A novel modeling and control method for three phase PWM converters［C］//IEEE 32nd Annual Power Electronics Specialists Conference，June 17－21，2001，Vancouver，BC，Canada，2001:102－107.

［6］李军徽，朱昱，严干贵.储能系统控制策略及主电路参数设计的研究［J］.电力系统保护与控制，2012，40(7):7－12.

LI Junhui，ZHU Yu，YAN Gangui.Research on the control strategy and the design of main circuit parameters of energy storage system［J］.Power System Protection and Control，2012，40(7):7－12.

［7］HAI Lin，PANOS J.Antsaklis.Stability and stabilizability of switched linear systems:A survey of recent results［J］.IEEE Transactions on Automatic Control，2009，54(2):308－322.

［8］马皓，毛兴云.基于混杂系统模型的DC/DC电力电子电路参数辨识［J］.中国电机工程学报，2005，25(10):50－54.

MA Hao，MAO Xinyun.Parameter identification of DC/DC power electronic circuits based on hybrid system model［J］.Proceedings of the CSEE，2005，25(10):50－54.

［9］陆益民，张波.DC/DC变换器的切换仿射线性系统模型及控制［J］.中国电机工程学报，2008，28(15):16－22.

LU Yimin，ZHANG Bo.Switched affine systems modeling and control of DC/DC converters［J］.Proceedings of the CSEE，2008，28(15):16－22.

［10］高明远.双向DC/DC变换器基于切换系统的建模与储能控制［J］.电力系统保护与控制，2012，40(3):129－134.

GAO Mingyuan.Modeling and energy storage control for bi-directional DC/DC converter based on switching system［J］.Power System Protection and Control，2012，40(3):129－134.

［11］李琼林，刘会金.基于切换系统理论的三相变流器建模及其稳定性分析［J］.电工技术学报，2009，24(11):89－95.

LI Qionglin，LIU Huijin.Modeling and stability analysis of threephase converter based on switching system theory［J］.Transactions of China Electro Technical Society，2009，24(11):89－95.

［12］高立群，景立.线性切换系统经周期切换渐近稳定性研究［J］.控制与决策，2005，20(5):541－544.

GAO Liqun，JING Li.Asymptotical stabilization of switched linear system via periodic switching sequences［J］.Control and Decision，2005，20(5):541－544.

［13］俞立.鲁棒控制—线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002.

［14］ZHANG Lixian，WANG Changhong.Stability and stabilization of a class of multimode linear discrete-time systems with polytopic uncertainties［J］.IEEE Transactions on Industrial Electronics，2009，56(9):3684－3692.

［15］ZHAI Guisheng，LIN Hai.Quadratic stabilizability of switched linear systems with polytopic uncertainties［J］.International Journal of Control，2003，76(7):747－753.

［16］Pascal Gahinet，Arkadii Nemirovskii.LMI control toolbox［C］//Proceedings of the IEEE Conference on Decision and Control，March 27－29，1994，York，England，1994:2038－2041.