基于网格法的NURBS自由曲线速度场规划

王丽梅， 李兵

(沈阳工业大学电气工程学院，辽宁沈阳 110870)

0 引言

数控机床正在向精密、高速、复合化的方向发展。具有代表性的直线电机XY二维平台系统，以其快速响应、准确定位和高可靠性广泛应用于高速自动化加工设备等领域［1－2］。

为提高XY平台系统的轮廓精确度，许多研究侧重于将各个单轴的跟踪误差作为控制目标，期望由降低各单轴跟踪误差来提高系统轮廓精确度［3－5］。但此类方法并不能完全解决双轴动态不一致等因素对轮廓精确度造成的影响。实际上，当系统执行轮廓任务时，各单轴跟踪控制器为减小跟踪误差驱使两轴偏离期望轮廓轨迹，使得实际轮廓轨迹半径小于期望轮廓半径，产生轨径缩减现象，因此，跟踪误差的减小并不能保证轮廓精确度的提高［6］。为解决单轴控制的不足，文献［7－8］分别采用不同的交叉耦合控制方法(cross－coupled control，CCC)减小系统的轮廓误差，其主要思想是通过获取各单轴的跟踪误差信息来实时估计轮廓误差，通过设计控制律对轮廓误差进行补偿，并将补偿量分解到各个轴上，以提高其协调性，最终减小轮廓误差。但其轮廓误差模型以跟踪误差为基础，因此，不适用于因高速、大曲率加工导致较大跟踪误差的情况。实际上，轮廓误差比跟踪误差更能反映轮廓运动情况，为了直接减小系统轮廓误差，有研究学者提出以建构速度场的方式规划轮廓运动系统的指令路径，将双轴协调控制转化为速度控制，通过减小各单轴的速度误差提高轮廓精确度。文献［9］首先提出速度场方法，利用速度场只与轨迹所在的位置有关而与时间无关的特点，使轮廓控制器的设计可以侧重于减小轮廓误差而非跟踪误差。文献［10－16］分别将速度场应用到机器人、机械手、健身器等协调控制系统中，通过设计相应的速度控制器以实现轮廓控制任务。可是，对于一般圆形和直线轨迹，其速度场的构建比较容易，而针对比较复杂的轨迹，其速度场难以利用一般几何方法构建。

为实现将双轴协调控制转化为单轴速度控制，提高系统轮廓精确度，本文针对速度场的构建方法进行深入研究，提出一种可适用于任意自由轨迹轮廓跟踪系统轨迹规划的方法。对于一般圆形轨迹，利用一般几何方法能够构建其速度场，而对于非圆形的自由轨迹，由于轨迹的时变性，其速度场难于构建，因此，基于方向场理论，以划分网格点的方式建构其速度场。最后，利用仿真与实验分别针对圆形和非圆形两种轨迹的轮廓跟踪情况进行对比分析来证明所提方案的可行性及正确性。

1 圆形轨迹

1.1 NURBS参数式曲线

为实现高速，高精度轮廓加工任务，采用非均匀有理B样条(non-uniform rational B－splines，NURBS)插补器作为轮廓控制系统的指令轨迹。在二维平面内，以参数式表示曲线P(u)为

其中:u为曲线参数，且0≤u≤1，px(u)、py(u)分别为曲线p(u)在X、Y轴的分量。以NURBS曲线方程表示为

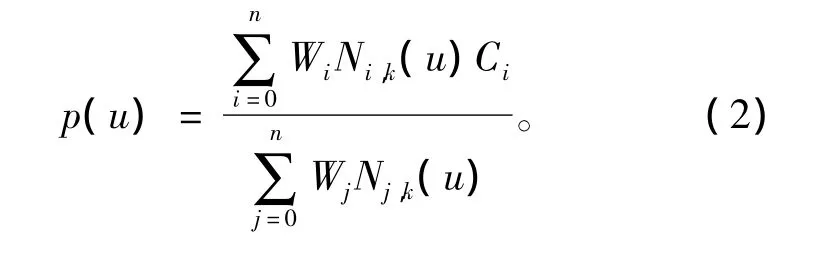
其中:Ci为控制点;Wi为对应控制点的权因子;Ni，k(u)为基函数，其可计算为

其中，［u0，u1，…，um］表示节点矢量，m=n+k+1。

1.2 圆形轨迹速度场的构建

空间速度场由多个速度向量构成，而速度向量可定义为空间中任意一点到指令轨迹的最短距离与该轨迹曲线的切线向量所构成。将此概念应用于二维平面，计算任意一点的速度向量，如图1所示。

图1 速度向量示意Fig.1 Diagram of velocity vector

图中，(x0，y0)为圆形轨迹的圆心坐标，r为圆形轨迹半径，q为平面中的任意一点，V为任意一点的速度向量为指令轨迹的切线向量，d为任意一点q与指令轨迹g(x，y)的最短距离向量，其交于轨迹于A点，因此，二维平面中任意一点的速度向量可计算为

其中，▽g(x，y)可计算为

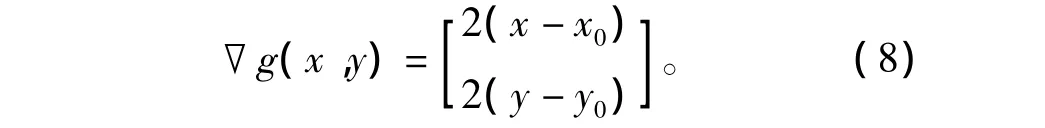
圆形轨迹g(x，y)可表示为

依照以上计算方法，将式(6)～式(9)分别代入式(5)能够计算出平面内任意一点的速度向量，而平面内所有点的速度向量集合就是所构建的速度场。

2 自由轨迹

2.1 自由轨迹速度场的构建

当系统指令轨迹是比较复杂的自由曲线时，由于轨迹具有任意性，距离向量d难以准确计算，因此，不能利用一般几何方法构建其速度场，本文基于方向场理论，采用网格点方法搭配插值的方式间接地建构其速度场。

根据方向场理论，在二维平面内选定一个矩形区域，这个区域的X轴与Y轴的范围区间为

在这个矩形区域内，以h为网格间距，n为网格点数量，定义每个网格点为

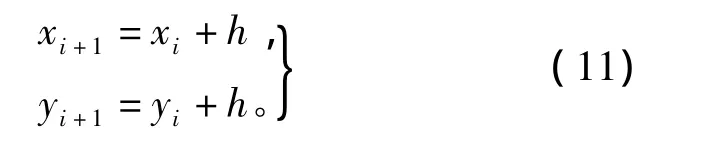
其中，i=0，1，…，n。一般地，对于平面内的每一个网格点(x，y)，都可以定义一个向量与过该点的曲线相切并指向该曲线解的方向，这个向量叫做方向向量，这些网格点上所有向量的集合就称为方向场，因此，任意一个网格点的方向向量可写为

根据初值问题的存在唯一定理可充分证明，如果在这个矩形区域内选定一个初始点，那么就能够得到一条以方向场所描述的运动轨迹。因此，根据方向场理论以网格点方法能够构建出任意轨迹的速度场，而当系统处于理想的控制条件下，运动系统沿着平面内箭头方向所得的轨迹就是指令轨迹，如图2所示。如果适当地调整相邻网格点的间距h，能够大幅度减小系统指令轨迹与由速度场编码轨迹之间的轮廓误差。

图2 网格点示意Fig.2 Diagram of grid point

当轨迹通过网格点时，利用方向场理论，能够计算出预先划定网格上的每点的速度向量，而当轨迹不在网格点上时，可利用间接插值方式计算其速度向量，具体方法如下。

1)当轨迹插值点在相邻两个网格点中间时，如图3所示。

图3 两点之间的速度向量构建Fig.3 Velocity vector construction for the point between two nearby grid points

其速度向量V按照下式计算，即

式中:v1x与v1y分别为v1在X轴与Y轴的分量;v2x与v2y分别为v2在X轴与Y轴的分量。

2)当实际轨迹在相邻4个网格点之间时，如图4所示，其速度可计算为

其中:v3x与v3y分别为v3在X轴与Y轴的分量;v4x与v4y分别为v4在X轴与Y轴的分量;α与β为常数，可计算为

图44 点之间速度向量场的构建Fig.4 Velocity vector field construction for the point between four nearby grid points

采用速度场方法可将指令轨迹的X、Y轴位置指令，转化为两轴的速度指令，利用速度场仅与当前位置有关而与时间无关的特点，将传统双轴协调控制转化为单轴速度控制，在后续控制器的设计上只需要设计单轴速度控制器减小各轴的速度误差，就能够提高系统轮廓精确度。

2.2 速度场连续性分析

文中以NURBS曲线作为系统的指令轨迹，由速度场的特点可知，每个网格点上的速度向量是唯一的，因此，为确保系统沿着平面内速度场的箭头方向所描绘的轨迹与指令轨迹是相同的，必须保证由所构建的速度场所编码的轨迹是唯一的，即保证所建构的速度场在二维平面内为连续函数，如图5所示。

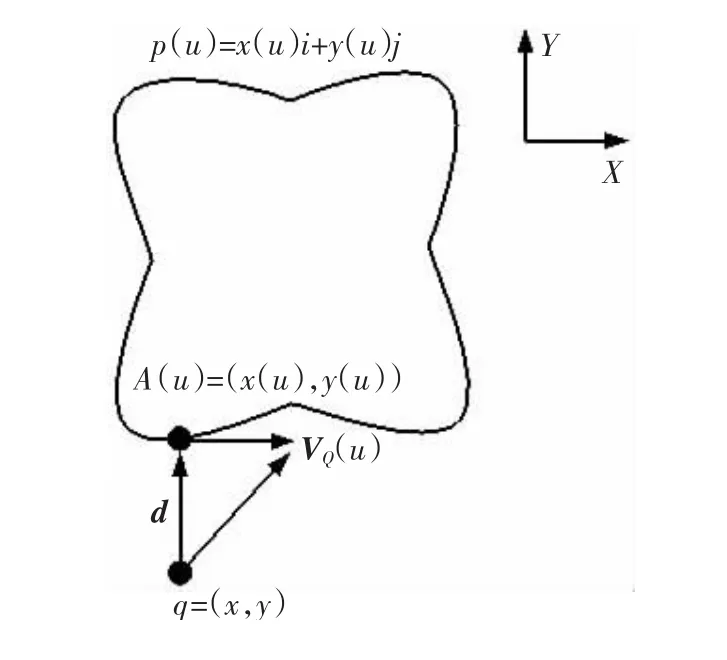
图5 自由轨迹速度向量示意Fig.5 Diagram of velocity vector for the free form contour

图中，p(u)为平滑封闭曲线且二次可微，q为XY平面内任意一点，令d为q点与曲线p(u)所形成的最短距离向量，A(u)为最短距离向量与曲线p(u)相交的插值点，VQ(u)为曲线p(u)插值点A(u)的切线速度向量。因此，定义平面内任意一点q的速度向量为

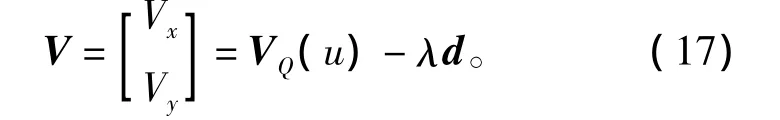
切线向量VQ(u)可计算为

根据距离向量的意义可定义距离函数为

距离函数的最小值为

其中，T为一个有界闭子集，在二维平面内，距离函数f(q，u)可重新写为

由于开根号函数均为连续函数，因此距离函数f(q，u)为连续函数，因此，距离函数最小值为连续函数，即保证距离向量在X轴与Y轴分量均为连续函数。

基于上述分析可知，速度场在X轴与Y轴的分量均为连续函数，即运动系统最终沿着平面内速度场的箭头方向能够收敛到指令轨迹上。

3 仿真分析

为了验证本文所提方案的可行性及正确性，利用Matlab对速度场的构建方法进行仿真，同时，为了证明以方向场网格点方法能够建构NURBS自由轨迹的速度场，利用所提方法建构圆形与四叶草两种轨迹的速度场，并将由速度场所编码的轨迹与指令轨迹之间的轮廓误差进行对比分析。

采用NURBS参数式模型作为系统的指令轨迹，适当地调整其控制点、节点向量及权重值后，分别得到圆形及四叶草两种轨迹，其图形参数如下。

按照选定的权重值、控制点与节点向量，分别得到圆形与四叶草两种轨迹，如图6、图7所示。

图6 圆形轮廓轨迹Fig.6 Circular contour trajectory

图7 四叶草形轮廓轨迹Fig.7 Four-leaf contour trajectory

针对圆形轨迹，利用一般几何方法构建其速度场，如图8所示。对于四叶草轨迹，基于方向场的网格点方法，选取网格点间距h=2 mm，经过反复调节，以插值的方式构建轨迹的速度场，如图9所示。从图8、图9中可以看出，对于圆形轨迹和四叶草轨迹，无论利用一般几何方法还是网格点方法，沿着速度场的箭头流形方向均能够编码指令轨迹，即利用速度场方法能够将指令轨迹在X、Y轴位置指令完全转化为X、Y轴的速度分量作为系统的指令输入，而所建构的速度场只与当前运动轨迹的位置有关而与时间无关，因此，利用速度场方法能够使后续控制器设计侧重于减小轮廓误差而非跟踪误差。

图8 圆形轮廓轨迹速度场Fig.8 Velocity vector field of circular contour trajectory

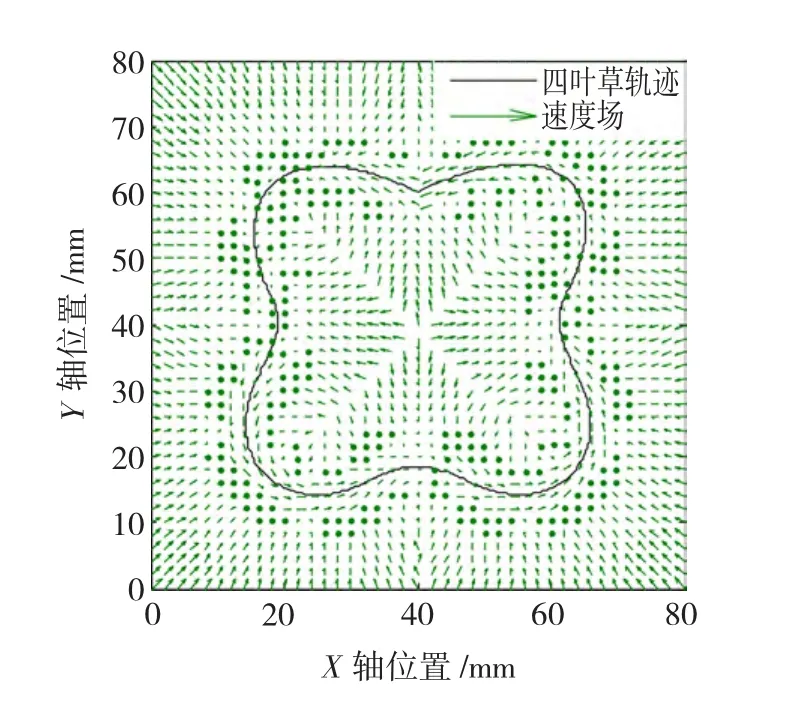
图9 四叶草轮廓轨迹速度场Fig.9 Velocity vector field of four-leaf clover contour trajectory

根据图8与图9，在以两种方法所构建的速度场所编码的两种轨迹与指令轨迹中分别选定150个与90个插值点，并分别计算两种轨迹与指令轨迹之间的轮廓误差，如图10、图11所示。

综合上述仿真结果，由图8～图11可知，采用方向场网格点方法能够构建任意NURBS自由轨迹的速度场，当网格间距为2 mm时，两种轨迹的轮廓误差分别保持在0～2 μm与0～1 μm之间。

图10 圆形轨迹轮廓误差曲线Fig.10 Contour error of the circular trajectory

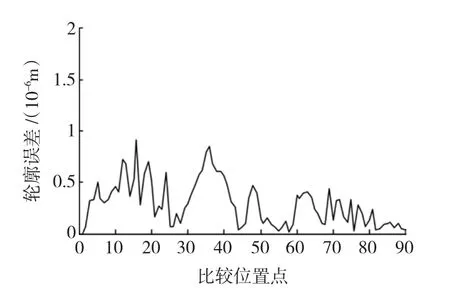
图11 四叶草轨迹轮廓误差曲线(h=2 mm)Fig.11 Contour error of the four-leaf clover trajectory(h=2 mm)

4 实验验证

为进一步验证速度场方法的有效性，搭建了基于速度场的XY平台实验系统，其实验装置如图12所示。

图12 实验测试系统Fig.12 Picture of the measure system

图12中，测试平台选用的是北京慧摩森公司生产的XY二维平台，X、Y轴位置传感器均采用美国GSI公司的Micro-E MercuryⅡ1600－40型光栅编码器，测试系统采用脉冲触发方式，实验所采用的直线电机为每个脉冲移动0.5 μm，在程序中将光栅尺采集的实际位置与测试系统的脉冲数做如下转换，即

pulse数=目标位置(μm)/0.5(μm)

为了便于数据采集，采用VC6.0++进行编程，将得到的实验数据写入数据库(ODBC)，并且将ODBC数据库与VC相连，将数据导入EXCLE，最后，利用Matlab将EXCLE中存储的轨迹规划位置、速度及光栅编码器的采样位置等数据导出，并绘制曲线如下。

将四叶草轨迹的初始网格距离由2 mm调整至1 mm，插值点增加到200个点时，由速度场编码的轨迹与NURBS指令轨迹的重合情况及两种轨迹之间的轮廓误差曲线如图13和图14所示。

由图可知，网格点之间的距离越小时，由速度场编码的轨迹与NURBS指令轨迹之间的轮廓误差越小，当网格间距h=1 mm时，指令轨迹与实际轨迹基本重合，四叶草轨迹的轮廓误差保持在0～0.5 μm之间。

图13 四叶草指令轨迹与实际轨迹Fig.13 Four-leaf clover desired path and output path

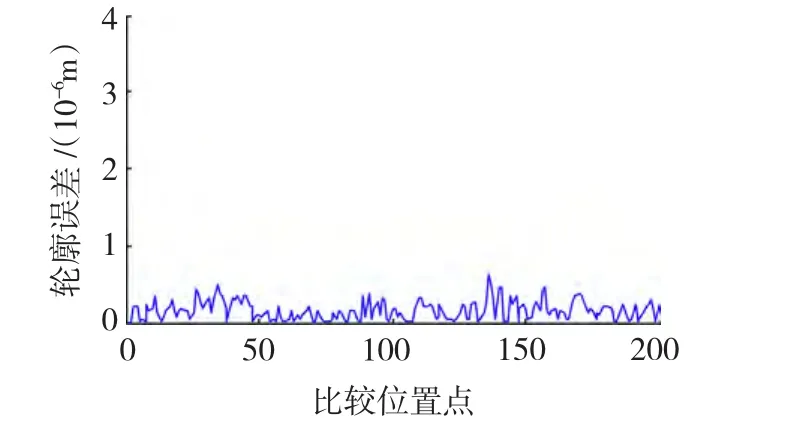
图14 四叶草轨迹轮廓误差曲线(h=1 mm)Fig.14 Contour error of the four-leaf clover trajectory(h=1 mm)

5 结论

本文针对圆形与四叶草两种轨迹，分别采用一般几何方法和划分网格法构建NURBS指令轨迹的速度场，通过对仿真与实验结果的对比分析得到以下结论:

1)针对任意NURBS自由轨迹，基于方向场理论，能够以划分网格的方式构建其速度场，而由此方法构建速度场所编码的轨迹与以一般几何方法构建速度场所编码轨迹的轮廓精确度基本相同;

2)针对同一种轨迹，通过适当地调整网格间距能够减小其轮廓误差，当网格点间距越小时，其轮廓误差值越小;

3)仿真结果表明，基于方向场理论，以网格点方法能够构建任意轨迹的速度场，通过适当调整网格间距使h=1 mm时，能够使四叶草轨迹的轮廓误差保持在0～0.5 μm之间，证明了该方法的可行性和有效性。

［1］郭庆鼎，王成元，周美文，等.直线交流伺服系统的精密控制技术［M］.北京:机械工业出版社，2000.

［2］王先逵.现代制造技术及其发展趋向［J］.现代制造工程，2008(1):1－8.WANG Xiankui.Modern manufacturing technology and its development［J］.Modern Manufacturing Engineering，2008(1):1－8.

［3］赵希梅，郭庆鼎.为提高轮廓加工精度采用DOB和ZPETC的直线伺服鲁棒跟踪控制［J］.电工技术学报，2006，21(6):111－114.

ZHAO Ximei，GUO Qingding.Linear servo robust tracking control based on DOB and ZPETC to improve the contour machining precision［J］.Transactions of China Electrotechnical Society，2006，21(6):111－114.

［4］YAN Zugen，SUN Lining，HUANG Bo.Research of a novel XY-table based on error compensation［C］//IEEE International Conference on Mechatronics and Automation，July 29－August 1，2005，Niagara Falls，Canada.2005:61－64.

［5］王丽梅，武志涛，孙宜标，等.直接驱动XY平台轮廓误差分析及法向交叉耦合控制［J］.电机与控制学报，2010，14(9):63－68.

WANG Limei，WU Zhitao，SUN Yibiao，et al.Contour error analysis and normal cross-coupled control for direct drive XY table［J］.Electric Machines and Control，2010，14(9):63－68.

［6］GEORGE T-C Chiu，TOMIZUKA M.Contouring control of machine tool feed drive systems:a task coordinate frame approach［J］.IEEE Transactions on Control System Technology，2001，9(1):130－139.

［7］丛爽，刘宜.多轴协调运动中的交叉耦合控制［J］.机械设计与制造，2006(10):166－168.

CONG Shuang，LIU Yi.Cross-coupling control in multi-axis coordinated motion［J］.Machinery Design＆Manufacture，2006(10):166－168.

［8］赵希梅，郭庆鼎.提高轮廓加工精度的零相位自适应鲁棒交叉耦合控制［J］.电工技术学报，2007，22(12):170－174.

ZHAO Ximei，GUO Qingding.Zero phase adaptive robust cross coupling control for improving the contour machining precision［J］.Transactions of China Eletrotechnical Society，2007，22(12):170－174.

［9］LI P Y，HOROWITZ R.Passive velocity field control of mechanical manipulators［J］.IEEE Transactions on Robotics and Automation，1999，15(4):751－763.

［10］LI P Y.Adaptive passive velocity field control［C］//Proceedings of the American Control Conference，June 2－4，1999，San Diego，USA.1999:774－779.

［11］MORENO-VALENZUELA J.Velocity field control of robot manipulators by using only position measurements［J］.Journal of the Franklin Institute，2007，44(8):1021－1038.

［12］HA C，CHOI F B，LEE D.Preliminary results on passive velocity field control of quadrotors［C］//Proceedings of the 29th URAI International Conference，November 26－28，2012，Daejeon，Korea.2012:378－379.

［13］CHEN C Y，CHENG M Y.Velocity field control and adaptive virtual plant disturbance compensation for planar contour following tasks［J］.IET Control Theory and Application，2012，6(9):1182－1191.

［14］MORENO-VALENZUELA J.On passive velocity field control of robot arms［C］//Proceeding of the 45th IEEE Conference on Decision and Control，December 13－15，2006，San Diego，USA.2006:2955－2960.

［15］ERDOGAN Ahmetcan，SATICI Aykut Cihan，PATOGLU Volkan.Passive velocity field control of a forearm-wrist rehabilitation robot［C］//IEEE International Conference on Rehabilitation Robotics，June 29－July 1，2011，Zurich，Switzerland.2011:5975433.

［16］YAMAKITA M，ASANO F，FURUTA K.Passive velocity field control of biped walking robot［C］//IEEE International Conference on Robotics and Automation，April 24－28，2005，San Francisco，USA.2005，3:3057－3062.