数学基础复习课的内容解析初探

●吴增生 (仙居县教育局教研室 浙江仙居 317300)

数学基础复习课的内容解析初探

●吴增生 (仙居县教育局教研室 浙江仙居 317300)

章建跃博士领衔的《中小学数学课程核心内容及其教学的研究》课题为一线教师进行规范系统地教学设计提供了明确的工作流程，其6个环节的教学设计流程可以促进教师深刻地理解数学、理解学生的学习、理解数学教学，在此基础上进行基于完整问题和任务序列的教学设计，提高课堂教学的针对性、科学性，为教师执教能力的发展提供了有效的途径.在6个环节的设计流程中，“内容和内容解析”是基础性的工作，通过“内容和内容解析”，理解相关内容的数学本质及其教育价值，明确教学重点，保证了教学设计方案的针对性，使核心内容的学习得到充分的资源保障，使其教育价值得到充分体现.基础复习课是一种特殊的课型，具有与新授课不同的教育价值和课堂结构，内容解析也有其自身的特点.

1 基础复习课的内容特点

复习是一种特殊的学习活动，它既有一般学习的特点又具有其自身的特点.从学习内容角度看，它与一般的数学内容学习的共性在于：都是对数量关系和空间形式的研究，其研究的最基本思想都是抽象概括的思想、推理(计算)的思想、数学模型的思想.复习课中学习内容区别于新授课的特点是：

1.1 结果性

复习课中学习的内容都是学生已经学习过的，在新授课的学习过程中，学生经历了新知识的探索、发现、证明和应用过程，其知识是带有更多的过程属性和单一的结果属性的综合体.如在整式概念新课学习中，学生对整式概念的理解更多地带有运算过程的理解.例如，把3ab看成是3×a×b，而在复习课中，需要引导学生把一个整式看成由一些数(包括具体的数和抽象的字母表示的数)通过代数运算得到的一个数.由于把整式看成运算结果——一个数，因此，整式之间还可以进行运算，从而进一步得到分式、根式等概念，建立整式有关知识之间、整式与其他概念之间的联系，使更多的符号运算成为可能.

1.2 系统性

复习课中涉及的知识在新授课学习中往往分散在不同的课中，需要在基础复习课中进行重新加工，建立这些原先分散的知识点之间的联系，使之成为具有良好结构的知识系统.例如，平行四边形包括相关概念(平行四边形、矩形、菱形、正方形等)、性质、判定，这些分散在不同课时中的知识需要在基础复习课中建立它们之间的相互联系，形成平行四边形相关知识的系统.

1.3 整体性

在新授课学习中，对知识的理解更关注细节(如形成过程、应用的经典模型、按照程序进行应用知识的操作等)，而在基础复习课中则更关注整体知识系统的理解，关注知识之间的联系，需要用更高的观点、更广阔的视野审视知识系统.例如，在新授课教学中，合并同类项、去括号法则的概括、记忆和应用是教学中关注的重点，在应用法则的过程中，是在把法则转化为操作程序的基础上对照程序进行运算操作的;而在整式加减的复习课中，则更需要关注用整式表示数量关系和整式的加减运算，需要把合并同类项法则和去括号法则再次概括到分配律水平，使这2个法则统一到更简单、更本质的原理——数系运算的分配律水平上，建立整式加减的知识系统(如图1).

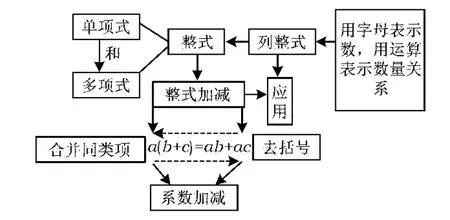
图1

综上所述，结果性、系统性和整体性是基础复习课中知识内容最显著的特征，与此相对应，基础复习教学中学生认知加工的对象是已经学习过的、分散的、相对孤立的知识;认知加工的方式是建立这些知识之间、这些知识与其他知识以及其典型应用问题之间的关联，而建立这些知识之间关联的有效方法是把这些知识概括到新的水平，用更高的观点、更广阔的视野进行知识的组织和系统化，这样，学生对相关知识的理解在相互联系和更高水平的概括中得到深化［1］，也就是说，认知重构是复习活动的核心.

2 基础复习课的内容解析解析什么

承上所述，基础复习课中的知识具有结果性、系统性和整体性，其核心认知活动是对相关知识的认知重构，建立新的、简约的知识系统.因此，基础复习课中内容解析的重点是对相关知识的相互联系、数学本质、地位作用的系统分析和对核心认知活动——知识系统重组、知识系统应用过程中教育价值的分析，从而确定教学重点.

2.1 分析本内容的内部结构

复习活动需要引导学生进行相关知识的系统化组织，这是复习的核心认知活动.由于复习课中涉及到的知识多，需要在回顾和理解相关知识的基础上进行知识结构的系统组织，把知识组织成简约的系统，引导学生“把书读薄”.除了引导学生把知识“压缩”成结果(用术语、符号等把知识缩略)外，还需要用更高的观点审视相关知识，建立起相关知识的内部联系.为了使学生对相关知识关联达到结构化、简约化的理解，教师在教学设计时，必须对本内容的内部结构进行高观点的分析.

2.2 分析本内容蕴含的核心数学思想方法

知识是研究数学的工具和数学研究的结果，思想方法则是怎样使用知识的思想和方法，是数学研究问题的基本套路.不仅如此，数学思想方法也是一种知识系统化组织的基本线索.分析内容的核心思想方法可以使复习教学具有更高的认知发展价值，使学生更好地理解知识中的灵魂，这对学生的长远发展是至关重要的.

2.3 分析内容要点与本质

把握内容的要点与本质就是用高观点理解当前的内容，分析当前内容的数学实质所在，只有把握了内容的要点与本质，才可以使知识之间的联系变得自然而简约.例如，整式加减运算的核心是分配律，而运算律是代数学的基石，代数学研究的是抽象符号之间的代数运算组成的系统，运算律是多项式理论、线性代数理论、向量空间理论以及群、环、域等理论的基础［2］.如果用抽象符号之间的运算来理解整式加减，其本质是字母表示数和运算律(特别是分配律)，这样，学生甚至不用记忆合并同类项法则和去括号法则，只要在数或字母运算中应用运算律，就可以自如地进行整式的加减运算.

2.4 分析本内容与外部的联系

要清楚一个内容的要点和本质，深刻理解本内容中的相关知识，需要在更大系统中分析，数学本身具有这样的特征(数学的不完备性)，这样，可以避免“身在此山中”而出现“不识此山的真面目”.在一个更大的系统中分析内容，其核心是分析本内容的知识系统与其外部的关联，主要是与其他内容、与不同的领域、与相关问题之间的联系.

2.5 分析本内容知识整理和应用过程的核心认知

活动和教育价值

在一个内容的复习活动中，需要学生进行特定的认知加工活动(如感知、表征、抽象概括、推理计算、建立模型、问题解决等活动)，开展这些活动的核心价值是提高认知加工的水平，体会数学思想方法.通过复习活动的认知分析，明确复习中需要发展的核心认知能力，可以为达成高阶目标提供正确的方向.例如，在等腰三角形的复习课中，很多教师把教学重点放在用分类讨论思想和方程思想解决等腰三角形相关问题上，这暴露出教学设计中对等腰三角形相关知识的核心价值的判断偏差.事实上，等腰三角形复习的核心价值是建立等腰三角形相关知识内部、等腰三角形和直角三角形、等腰三角形和轴对称之间的联系，发展空间观念、几何直观和推理能力.

2.6 确定教学重点

内容解析的主要作用是理解内容的数学本质和相互联系，在此基础上明确教学重点，引领教学过程设计.使课堂资源向核心和重点内容倾斜，保证宝贵的课堂时间用到重要的事情上.

3 基础复习课的内容解析怎样做

(1)分析本内容的内部结构，既可以采用知识产生、发展的线索，也可以用知识分类的方法，还可以用数学思想方法作为线索进行分析.例如，整式加减一章，用知识分类的方法进行分析如下：本章核心是学习做2件事情：一是列整式表示数量关系;二是整式的加减运算.顺着这2点，可以延伸出字母表示数、从数到字母的抽象、整式求值、同类项及其合并、去括号等，采用这种分析方法，可以形成如图2所示的本章知识结构.如果采用知识形成的线索分析，则是从字母表示数出发，得到列整式表示数量关系的方法，通过对列出式子的运算结构的分析;从对字母运算的类型分析，最简单的是只对字母的乘法运算(即单项式)，接着是单项式的加减得到多项式，并进一步得到整式，再研究整式的运算，得到合并同类项法则和去括号法则.这样，可以得到如图3所示的知识结构.如果分析本章的数学思想方法和认知活动，可以发现本章最核心的思想是从具体数到字母表示的一般数的抽象思想、化整式加减运算为系数加减运算的数学转化思想;本章的核心认知活动是字母表示数中从具体数到一般数的抽象、合并同类项法则和去括号法则的概括、整式加减运算过程的推理、把合并同类项和去括号统一到分配律的概括.这样，可以得到如图4所示的知识结构.

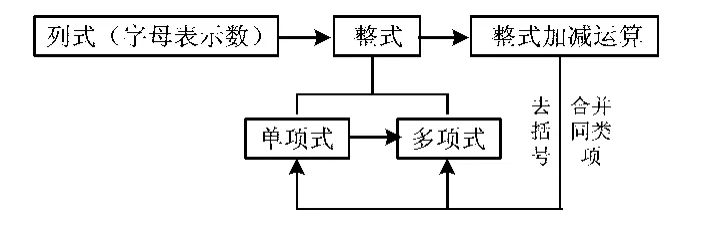
图2

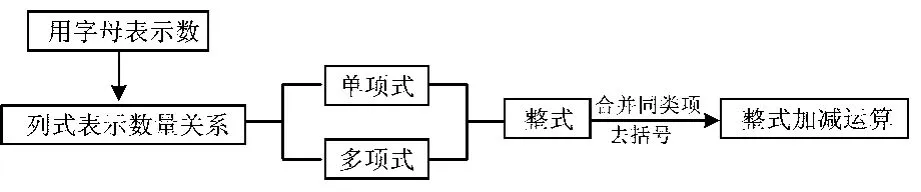
图3

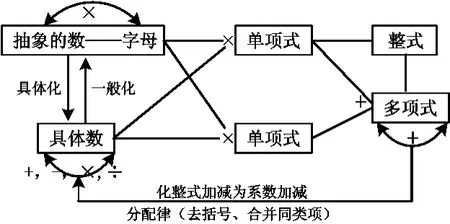
图4

(2)从知识的生成过程和应用过程中挖掘核心数学思想方法.如整式加减一章，在列整式表示数量关系中、在法则形成过程中体现了数学抽象的思想，在法则应用过程中体现了化整式加减为系数加减的转化思想.

(3)寻找要点，就是寻找能支撑其余知识或后继学习的知识点，确定本质就是要确定要点在支撑其他知识中存在的关键要素，如核心的思想或知识.如在整式加减一章中，列整式表示数量关系支撑着今后的列方程、列函数式等重要认知操作，是本章的要点;去括号和合并同类项是整式运算、分式运算、二次根式运算及解方程的基础，因此，这也是要点.列整式的关键是用字母表示数和运算表示数量关系，合并同类项和去括号的关键是运用分配律.因此本章内容的本质是从具体数到字母表示数的抽象，用分配律把整式加减转化为系数加减，实现整式表示数量关系的简约化.

(4)分析本内容与外部的联系，主要从以下3个方面进行：①分析本内容的产生背景，即知识是从哪里来的;②本内容与后继学习的联系，即知识到哪里去;③本知识与相关问题的典型联系，即知识主要有什么用.

例如，整式来自于用字母表示数、用运算表示数量关系，这里有3次概括：第1次的概括是把具体的数一般化并用字母表示;第2次是对用字母表示的数进行乘法运算得到单项式、把单项式进行加减运算得到多项式;第3次则是把多项式和多项式统称整式(如图5).

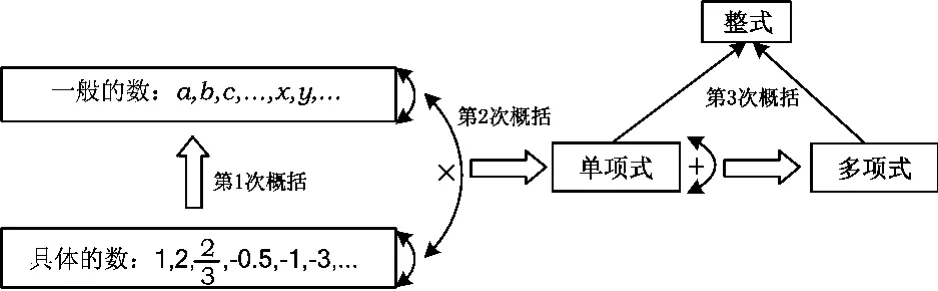
图5

而类比数的运算，研究整式的运算，还可以研究整式的乘除运算及因式分解、分式、根式运算等，这些运算的核心仍然是字母表示数与运算律.这样，就把具体数的运算(算术运算)拓展到数学符号的运算(代数运算)，进一步，可以发展到方程和函数理论.另外，用字母表示的数具有一般性，在刻画数量关系和数学规律中具有重要作用.

(5)从知识形成过程、系统化结构整理过程和应用过程中筛选出对今后学习和生活具有重要作用的认知活动，使教学过程设计中有重点地发展这些核心的认知加工水平.如在用字母表示数、列整式中的抽象、对运算结构的观察、在合并同类项法则和去括号法则中的概括、整式加减过程中的计算(推理).作为基础复习课，应对本章学习的这些知识进行系统化组织，并用贯穿本章的核心思想建立知识之间的联系，提升对符号化和运算律这两大代数本质的理解.结合前面的分析，就可以确定出本章复习教学的核心教育价值是：学习数学知识系统化组织的方法，优化知识结构，体会从数的运算到符号运算的抽象，学习最简单的代数符号运算——整式加减，并能用整式加减运算描述与研究简单的数量规律，体会“化式运算为数运算”的思想;发展数学抽象概括能力和推理计算能力.进一步，可以确定本章复习课的教学重点是：用字母表示数和分配律对本章知识进行系统化组织，用整式表示数量关系和整式的加减运算.

［1］项武义.基础代数学［M］.北京：人民教育出版社，2011.

［2］吴增生，齐秀华.基础复习课的核心任务、认知特点与教学策略［J］.中国数学教育：初中，2011(1/2)：86-93.

吴增生，1962出生，浙江仙居人.浙江省特级教师，省基础教育课程改革初中数学专家组成员，省第六届义务教育教材审定委员，人民教育出版社新版教科书社外作者、教师教学用书八年级下册社外主编、教科书培训专家，台州市名师工作室主持人.主要从事中学数学教育研究，已出版专著4部，有60多篇论文分别在《数学教育学报》、《数学通报》、《中学数学教学参考》、《中国数学教育》、《中学教研(数学)》等杂志上发表，截止目前有15篇被人大书报资料中心全文转载，10多篇论文被收录.