区域图案的周期性

●李世杰 (衢州市教育局教研室 浙江衢州 324002) ●李 盛 (衢州市第一中学 浙江衢州 324000)

区域图案的周期性

●李世杰 (衢州市教育局教研室 浙江衢州 324002) ●李 盛 (衢州市第一中学 浙江衢州 324000)

1 问题的提出

人行道上镶嵌的地砖，是用一些形状、大小完全相同的一种或几种地砖进行拼接，彼此之间不留空隙、不重叠铺成的，给我们整块区域周而复始的感觉.因此，研究平面图案是否具有周期性，是有现实意义的.

2 周期区域和方向周期的定义

类比函数的周期性，我们给出周期区域和方向周期的定义：

周期区域对于区域f(x)≥0(或≤，＜，＞，=之一)，如果存在一个非零常向量T=(T1，T2)，使得当x取定义域D(⊆R2)内的每一个值时，都有f(x+T)=f(x)，那么区域f(x)≥0(或≤，＜，＞，=之一)叫做周期区域，非零常向量T叫做这个区域的周期.

如果在所有的周期中存在一个模最小的非零常向量T，那么这个周期就叫做最短模周期.

方向周期在平面上，若 f(x+T1，y)=f(x，y)，x∈E 或 f(x，y+T2)=f(x，y)，y∈G，则分别称区域 f(x，y)≥0(或≤，＜，＞，=之一)为 x，y方向的周期区域(简称周期域)，称T1，T2分别是区域f(x，y)≥0(或≤，＜，＞，=之一)x，y方向的横向周期和纵向周期.

在区域的某一方向，如果在所有的方向周期中存在一个最小的正数，那么这个最小的正数就叫做横向或纵向最小正周期，简称最小正周期.

需要指出的是，区域的周期和区域的方向周期不是完全一致的.

(1)如果T1是区域 f(x，y)≥0(或≤，＜，＞，=之一)的横向周期，则(T1，0)是区域 f(x，y)≥0(或≤，＜，＞，=之一)的一个周期;如果T2是区域f(x，y)≥0(或≤，＞，＜，=之一)的纵向周期，则(0，T2)是区域 f(x，y)≥0(或≤，＜，＞，=之一)的一个周期.如果 T1，T2同时是区域 f(x，y)≥0(或≤，＜，＞，=之一)的横向周期和纵向周期，则(T1，T2)是区域 f(x，y)≥0(或≤，＜，＞，=之一)的一个周期.

(2)当非零常向量 T=(T1，T2)是区域 f(x，y)≥0的一个周期时，T1，T2不一定是区域 f(x，y)≥0的横向周期和纵向周期，即当f(x+T1，y+T2)=f(x，y)时，f(x+T1，y)=f(x，y)，f(x，y+T2)=f(x，y)不一定恒成立.

3 周期区域的性质

周期区域在自然界是客观存在的.如果我们能确定一个区域具有周期性，那么只要研究一个周期内的区域图案的特性，就能用有限探究无限，推知整个区域也具备这些特性.

根据周期区域的定义，我们可推出周期区域的一系列性质：

(1)若T是区域D的一个周期，则k·T(k∈N*)都是区域D的周期.

若T是区域D的一个周期，由于

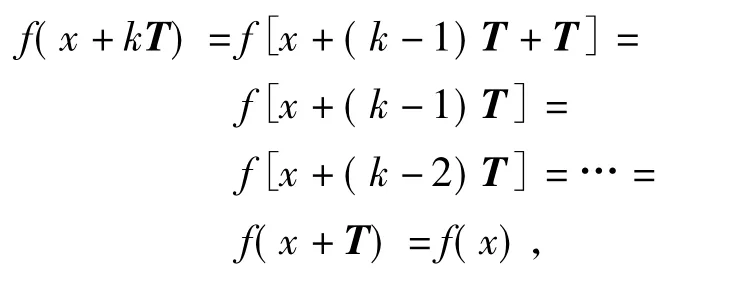
则k·T(k∈N*)都是区域D的周期.

但要注意：k·T(k≠0，k∈Z)不一定是区域D的周期，如函数f(x)=sinx(x∈R+)只有x轴方向的正周期 T=2kπ(k∈N*)，没有负周期;函数f(x)=cosx，x∈( －∞，0)，只有 x轴方向的负周期T=2kπ(k∈CZN)，没有正周期.

(2)不是每一个周期区域都有最短模周期.

如函数f(x)=1(x∈R)，所有正数都是f(x)在x方向的周期，但正数集中没有最小数，因此函数f(x)=1(x∈R)是周期函数，但没有x方向的最小正周期;又如函数

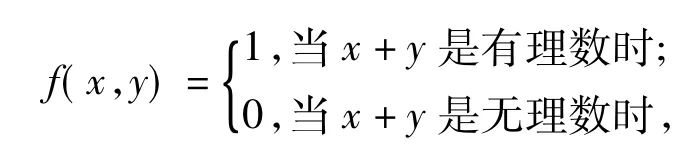
容易证明：任意有理数对(T1，T2)都是它的周期，但正有理数集中没有最小数，从而相应的周期区域也没有最短模周期.

(3)周期区域纵向或横向(至少一端)无界.

若区域f(x)≥0(或≤，＜，＞，=之一)是 D(⊆R2)上的周期区域，则对任意的n∈N*，f(x+nT)=f(x)，当n→∞时，由于T≠0，因此x+nT纵向或横向(至少一端)无界.

推论仅仅在有限个点上没有定义的区域一定是非周期区域.

(4)如果f(x，y)有2个独立的方向周期，就一定有无数多个方向周期.

如果T1是区域f(x，y)≥0(或≤，＜，＞，=之一)的横向周期，则 nT1(n∈N*)都是区域 f(x，y)≥0(或≤，＜，＞，=之一)的横向周期;如果T2是区域f(x，y)≥0(或≤，＜，＞，=之一)的纵向周期，则mT2(m∈N*)都是区域 f(x，y)≥0(或≤，＜，＞，=之一)的纵向周期.如果T1，T2同时是区域f(x，y)≥0(或≤，＜，＞，=之一)的横向周期和纵向周期，则(nT1，mT2)都是区域 f(x，y)≥0(或≤，＜，＞，=之一)的周期.

(5)如果 T1≠0，T=(T1，T2)是区域 f(x，y)≥0的一个周期，则在直线方向，f(x，y)以为周期.

可见性态好的区域，可以同时具有多个方向的方向周期.

4 周期区域的判断

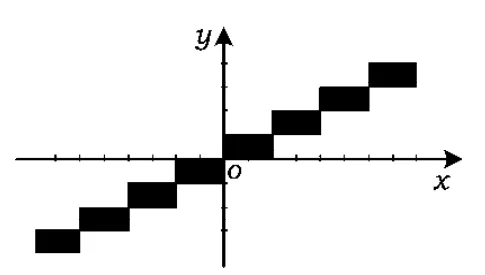
图1

相应区域图案在x轴方向正分周期最小为2，且y轴方向正分周期最小为1，在一个周期内画出图案为矩形闭区域：0≤x≤2，0≤y≤1，作周期延拓即可得方程的区域图案如图1所示.

例2判断由不等式|y|≤2－2|sinx|约束的区域图案的周期性.

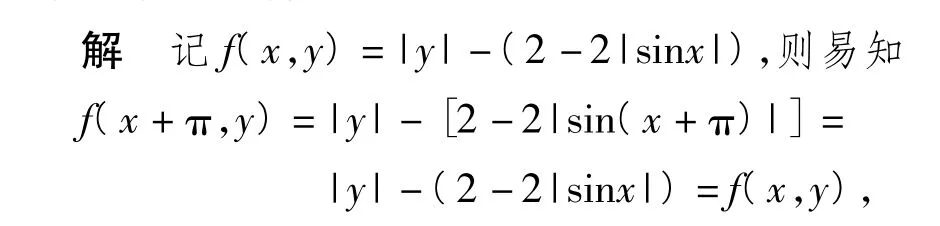
故所给不等式|y|≤2－2|sinx|约束的区域是周期区域，一个周期是(π，0)或横向周期为π.

注作曲线|y|=2－2|sinx|的图案如图2所示，是周期曲边菱形.

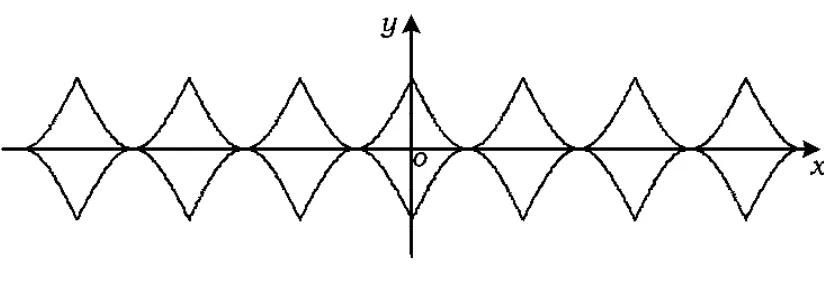
图2

相应地，所给不等式|y|≤2－2|sinx|约束的区域是如图3所示的周期曲边菱形闭区域图案：

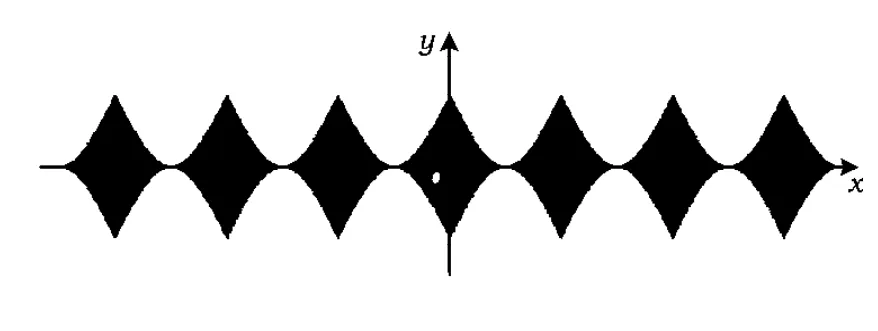
图3

例3判断数阵{(x，y)|x=n，y=2m，n，m∈N}的周期性.

解记 g(x，y)={(x，y)|x=n，y=2m，n，m∈N}，容易验证同时满足

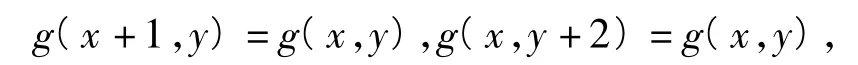
可见所给数阵是周期数阵，说明同时拥有2个垂直的方向周期：x轴方向最小正周期为1，y轴方向最小正周期为2，在直线y=2x方向最小正周期为

注g(x，y)有2个独立的方向周期，就一定有无数多个方向周期.例3中n，2m分别是g(x，y)的方向周期，则都是 g(x，y)的方向周期.

例4判断由方程1+siny=|sinx|+|cosx|约束的区域图案的周期性.

解由于容易得知：题给方程约束的区域图案最小的横向正周期为π，最小的纵向正周期为2π.故区域图案的最短模周期是(π，2π).

例5判断由不等式|y|≤2|sinx|－1约束的区域图案的周期性.

解曲线|y|=2|sinx|－1约束的图案是一个曲边菱形与一个金鱼形交替的周期图案(如图4).

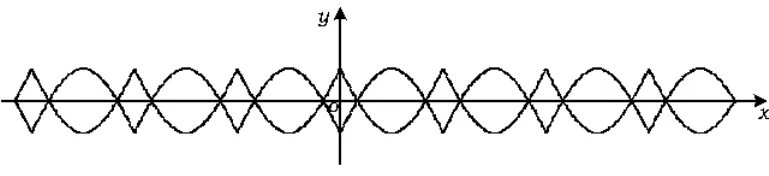
图4

相应的不等式给出的是金鱼形闭区域|y|≤2|sinx|－1的周期图案(如图5).

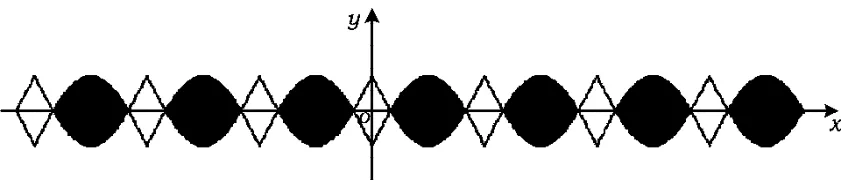
图5

注交替出现的菱形闭区域由不等式2|sinx|－1≤|y|≤1约束.

例6判断由不等式sin|y|≤sin|x|约束的区域图案的周期性.

分析根据文献［1］，知函数 u=sin|x|不是周期函数，可猜想由不等式sin|y|≤sin|x|约束的区域图案也不是周期区域.下面用反证法证明.

证明如果由不等式sin|y|≤sin|x|约束的区域图案是周期区域，则存在非零向量(T1，T2)，对任意的实数对(x，y)，

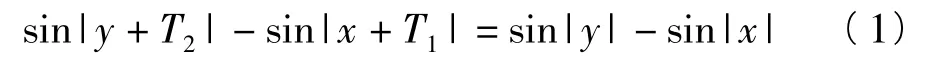
恒成立.令 x=y=0，得

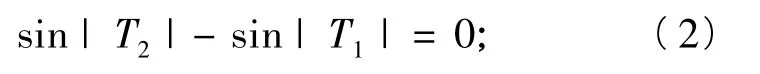
再令 x= － T1，y=0，得

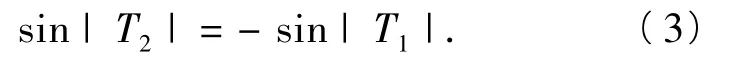
联立式(2)，式(3)得

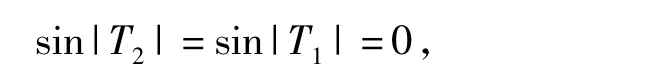
因此 T1=kπ，T2=pπ，k，p∈Z，但 kp≠0.再令 x=0，由式(1)得

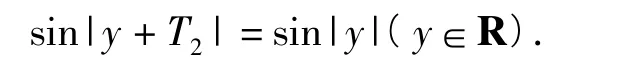
根据文献［1］，T2不存在.故假设不真，由不等式sin|y|≤sin|x|约束的区域图案不是周期区域.

注一般地，非周期区域的判定可用反证法，如本例.

应用方程或不等式刻画的周期区域，可以得到各种各样的数学花纹和数学图案.而且一些周期区域的图案十分优美.最后需要指出的是，我们定义的周期区域是广义的周期区域，本文只是初步研究了具有良好性态且周而复始的理想的周期区域.对于特殊情况的一些个例，文献［1］中已作过论述，这里不再展开讨论.

［1］李世杰.周期函数论［M］.杭州：浙江大学出版社，2005.

［2］李世杰，李盛.函数元不等式的理论及其应用［M］.杭州：浙江大学出版社，2011.

［3］李世杰.周期函数和周期数列［M］.杭州：浙江大学出版社，2008.

［4］李世杰，李盛.平面区域的对称性［J］.中学教研(数学)，2013(1)：26-30.