比较大小时构造函数应注意的几个原则

●楼可飞 (诸暨市教师进修学校 浙江诸暨 311800)

比较大小时构造函数应注意的几个原则

●楼可飞 (诸暨市教师进修学校 浙江诸暨 311800)

观察近几年高考中有关导数的解答题，几乎题题涉及比较大小、极值或最大(小)值，在比较大小时常常需要构造函数，这时应注意3个原则.

1 齐次性原则

要比较j与k的大小，只要比较分子z与0的大小.为了向b－a看齐，将分子变形为

构造函数g(t)=(t－2)et+t+2，这里t=b－a＞0.导函数

从而函数g'(t)在t＞0上单调递增，于是

因此函数g(t)在t＞0上单调递增，即

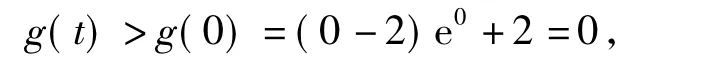
亦即分子 z＞0，差 c＞0，故 j＞k.

这里进行了2次求导：g'(t)，g″(t).若求导一次即可解决问题，则应如何构造函数?

图1

图2

2 整式化原则

例3设l为曲线在点 A(1，0)处的切线.

(1)求l的方程;

(2)证明：除切点A之外，曲线C在直线l的下方.

(2013年北京市数学高考试题)

当 x=1 时，y=0，y'=1，得直线 l为 y=x－1.

图3

于是函数h(x)在(0，1)上单调递减，在(1，+∞)上单调递增，故函数h(x)在(0，+∞)上有最小值h(1)=0，h(x)≥0，即

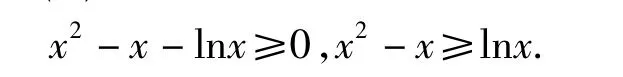
式(1)为分母中含有求知数x的不等式，而式(2)则为分母中不含有求知数x的不等式，这一等价的过程不妨称为整式化.

3 对数化原则

一般地，有：

(1)如果 a ＞0，且 a≠1，则

(2)如果 a＞1，则

(3)如果0＜a＜1，则

例5设函数f(x)=axn(1－x)+b(x＞0)，n为正整数，a，b为常数.曲线 y=f(x)在(1，f(1))处的切线方程为x+y=1.

(1)求 a，b的值;

(2)求函数f(x)的最大值;

(2012年湖北省数学高考试题)

分析(1)导函数

于是函数g(t)在t∈(1，2］上单调递增，故g(t)＞g(1)=0，即式(5)成立.

例6已知函数f(x)=x2lnx.

(1)求函数f(x)的单调区间;

(2)若对任意t＞0，存在唯一的s使t=f(s)，设s关于t的函数为s=g(t)，证明：当t＞e2时，有

(2013年天津市数学高考试题改编)