Weitzenbock不等式的一个有趣隔离

●秦庆雄 范花妹 (漾濞县第一中学 云南漾濞 672500)

Weitzenbock不等式的一个有趣隔离

●秦庆雄 范花妹 (漾濞县第一中学 云南漾濞 672500)

1919年，Weitezenbock提出了关于三角形的著名不等式：，当且仅当△ABC为等边三角形时，等号成立.关于它的推广与加强被广泛研究，但大多数是增加不等式右边的项数，如著名的Finsler-Hadwiger不等式当且仅当△ABC为等边三角形时，等号成立.本文从新的角度给出它的一个有趣隔离如下：

定理在△ABC 中，设 a，b，c分别为 BC，CA，AB 的边长，相应于顶点 A，B，C 的中线长为 ma，mb，mc，内角平分线长为 wa，wb，wc，高线长分别为 ha，hb，hc，△ABC 面积记为 S，则

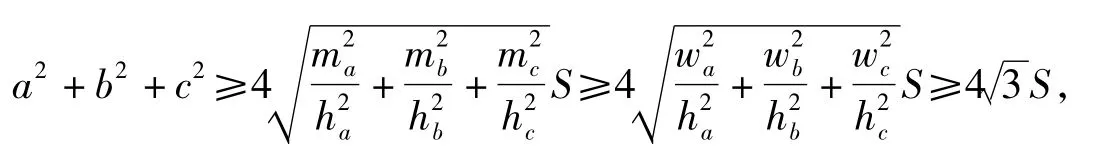
当且仅当△ABC为等边三角形时，等号成立.

我们先证以下引理.

引理在△ABC 中，相应于顶点 A，B，C 的中线长为 ma，mb，mc，内角平分线长为 wa，wb，wc，高线长分别为 ha，hb，hc，则

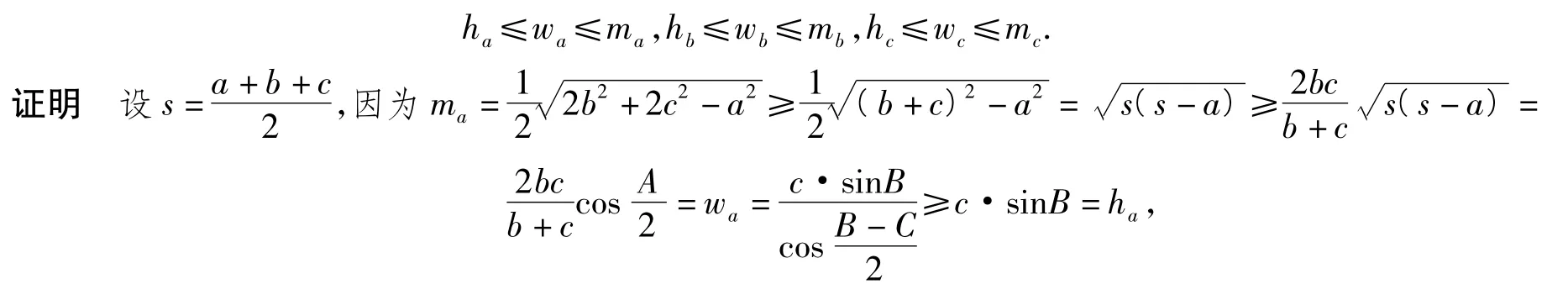
由上述证明过程可获得一个有趣的恒等式：在△ABC中，设a，b，c分别为BC，CA，AB的边长，相应于顶点 A，B，C 的中线长为 ma，mb，mc，△ABC 面积记为 S，则

文末，笔者提出一个猜想，供有兴趣的读者探究.

猜想在△ABC 中，设 a，b，c，分别为 BC，CA，AB 的边长，相应于顶点 A，B，C 的中线长为 ma，mb，mc，内角平分线长为 wa，wb，wc，高线长分别为 ha，hb，hc，△ABC 的面积记为 S，则

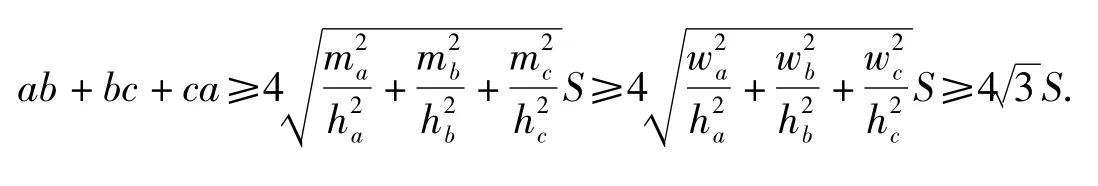
［1］博特马.几何不等式［M］.单墫，译.北京：北京大学出版社，1991：46-49.