一道概率习题的探究

●陈薛琴 (龙港第二高级中学 浙江苍南 325802)

一道概率习题的探究

●陈薛琴 (龙港第二高级中学 浙江苍南 325802)

笔者基于教材中一道概率课后习题，探究了“3局2胜、5局3胜与7局4胜制”下某选手获胜的概率，并推广到了一般的“2k+1局k+1胜制”的概率公式.

1 问题的提出

题目甲、乙2名选手比赛，假设每局比赛甲胜的概率为0.6，乙胜的概率为0.4，那么采用3局2胜制还是采用5局3胜制对甲更有利?你对局制长短的设置有何认识?每局比赛相互独立，甲胜的局数X服从二项分布.

(人教A版《数学(选修2-3)》习题2.2B组第1题)

方法1在3局2胜制下，X～B(3，0.6)，事件{X≥2}表示“甲获胜”，则甲胜的概率为

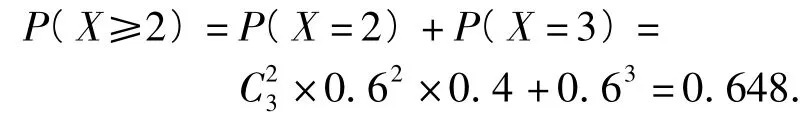
在5局3胜制下，X ～B(5，0.6)，事件{X≥3}表示“甲获胜”，则甲胜的概率为

方法2在3局2胜制下，设“甲获胜”为事件C，“前2局甲都胜”为事件A，“前2局甲胜1局，最后1局甲胜”为事件B，则C=A∪B，事件A与B互斥，则甲胜的概率为

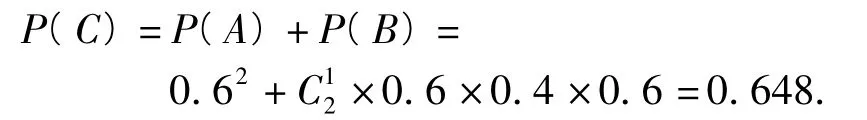
在5局3胜制下，设“甲获胜”为事件D，“前3局甲都胜”为事件A，“前3局甲胜2局，第4局甲胜”为事件B，“前4局甲胜2局，第5局甲胜”为事件C，则D=A∪B∪C，A，B与C这3个事件两两互斥，则甲胜的概率为

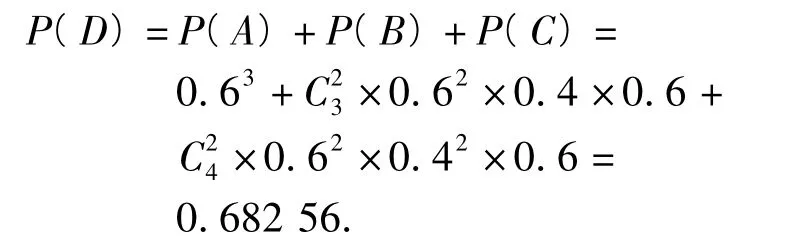
评析这2种计算方法的概率相等.对一般的情况成立吗?

2 “3局2胜、5局3胜与7局4胜制”下甲胜的概率

甲、乙2名选手比赛，设每局比赛甲胜的概率为x.若采用3局2胜制，则甲胜的概率为：

方法1设甲获胜的局数为X，则X～B(3，x)，事件(X≥2)表示“甲获胜”，则甲胜的概率为

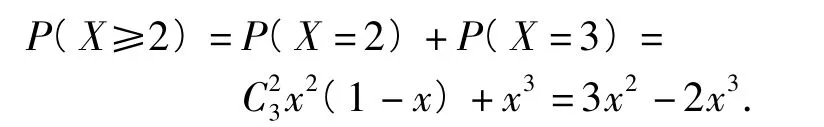
方法2设“甲胜”为事件C，“前2局甲都胜”为事件A，“前2局甲胜1局，最后1局甲胜”为事件B，则C=A∪B，事件A与B互斥，则甲胜的概率为

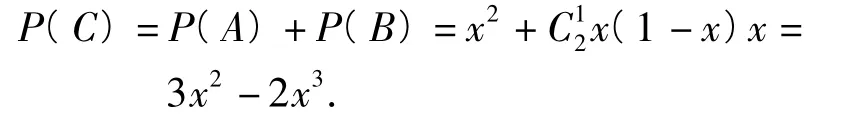
评析经过论证：在3局2胜制下，这2种计算方法甲胜的概率都为

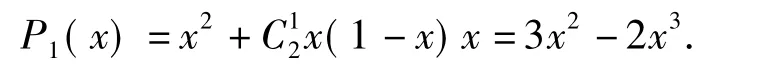
同理应用这2种方法，若采用5局3胜制，则甲胜的概率为

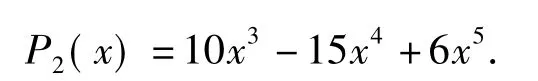
若采用7局4胜制，则甲胜的概率为

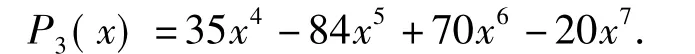
事实上以3局2胜制为例，方法1中比赛进行3 局甲胜出，可分为 4 种情况：(1，1，0)，(1，0，1)，(0，1，1)，(1，1，1).其中(1，1，0)表示前 2 局甲胜第3局甲负.而方法2是谁先胜出2局就停止比赛.在前2局甲胜的条件下，第3局不管甲胜还是负，最终甲胜是必然事件.这2种计算方法本质上是一样的，证明如下：

3 3种比赛制度的联系

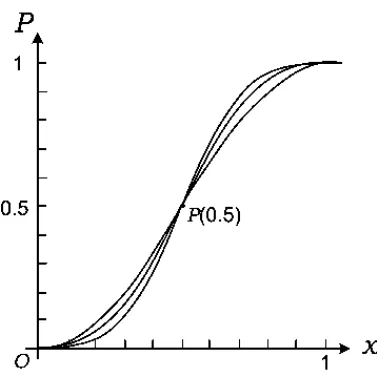
图1

直观感知通过观察“3局2胜、5局3胜与7局4胜制”下甲胜的概率函数图像(如图1所示)，发现3个图像恒过定点P(0.5)，关于点P中心对称，且在点P处的切线斜率为

在7局4胜制下，甲胜的概率函数在x=0.5处导数为

故3个概率函数的图像在点P(0.5)处的切线斜率

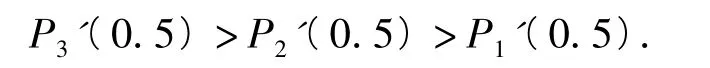
评析在实际问题背景中，当每局比赛甲胜的概率大于0.5时，比赛的总局数越多甲胜的概率越大.比赛局数越少，对乙越有利;比赛局数越多，对甲越有利.因此，比赛局数越多越公平.

4 “2k+1局k+1胜制”下甲胜的概率

甲、乙2名选手比赛，设每局比赛甲胜的概率为p，设甲获胜的局数为 X，则 X ～B(2k+1，p)，事件{X≥k+1}表示“甲获胜”，则2k+1局k+1胜制下甲胜的概率为