由教材母题解析2014年中考复习策略

●邱亦欣 (南京外国语学校 江苏南京 210008)

由教材母题解析2014年中考复习策略

●邱亦欣 (南京外国语学校 江苏南京 210008)

近几年各省市的中考数学试题突出了对数学思想方法、数学理性思维及数学实际应用能力的考查，注重通性、通法，淡化解题技巧.多数试题与课本例题、习题相近，有的直接由教材母题变形而来，即使是要求较高的“压轴题”的解题思路和方法也大都能在课本上找到“原型”，由此启发我们在中考复习阶段一定要回归课本，夯实基础，以不变应万变.

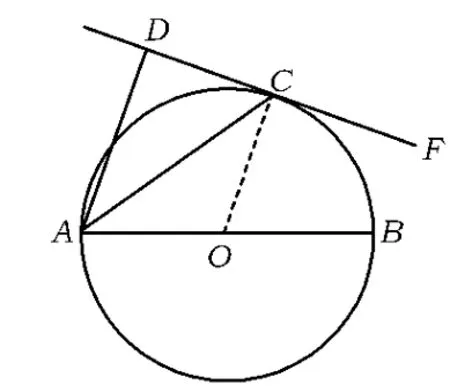
图1

苏教版《数学》九年级上册第153页的第9题如下：

母题如图1，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为 D，若∠BAD=80°，求∠DAC的度数.

分析要求∠DAC的度数，可考察∠DAC与已知角∠BAD的关系，“遇切点连半径”，联结OC.

由OC∥AD及OC=OA可得AC平分∠BAD.

解 如图1，联结OC.由DC切⊙O于点C，知

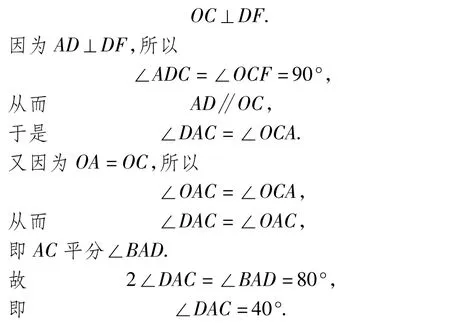
这道计算题可改为更一般性的证明题：

如图1，已知AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D，求证：AC平分∠DAB.

我们还可以作如下的变形和探究：

变形1交换题设与结论

探究1如图1，AB为⊙O的直径，C为⊙O上一点，且 AD⊥CD，AC平分∠DAB，求证：CD是⊙O的切线.

分析联结OC，要证明CD是⊙O的切线，只需证OC⊥CD.因为 AD⊥CD，所以只需证 OC∥AD，由 OA=OC和AC平分∠DAB，可证∠DAC=∠OCA，因此 OC∥AD.

探究2如图1，AB为⊙O的直径，C为⊙O上一点，过点C的切线交AD于D，AC平分∠DAB，证明：AD⊥CD.

分析联结 OC，要证明 AD⊥CD，只需证∠DCA+∠DAC=90°.由于 CD是切线，因此∠DCO=∠DCA+∠ACO=90°，故只需证∠DAC=∠ACO，这可由OA=OC和AC平分∠DAB来证得.

探究3如图1，若点A，B，C在⊙O上，AD和过点 C的切线互相垂直，垂足为 D，AC平分∠DAB，试说明：AB为⊙O直径.

分析联结OA，OC，要证明AB为⊙O直径，只需证明点A，O，B共线，即证∠CAO=∠CAB.

综上可知：在图1中，由“AB为⊙O的直径”、“CD是⊙O的切线”、“AC平分∠DAB”、“AD⊥CD”中任意3个作为条件都可以推出第4个成立.因此在中考复习时，适当的交换题设与结论，形成新的命题，论证其成立与否的过程，其实就是对图形本身和问题内在联系的再消化，有利于发展学生的思维，提高灵活运用知识解决问题的能力.

变形2延伸与拓展

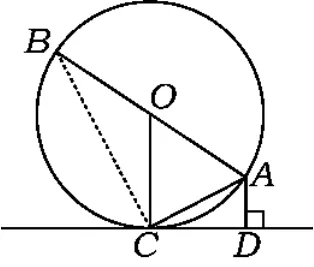
图2

探究1如图2，AB是⊙O的直径，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD，垂足为D，求证：

(1)∠AOC=2∠ACD;

(2)AC2=AB·AD.

分析(1)要证明∠AOC=2∠ACD，只需证明∠AOC=2(90°－∠ACO)，即证∠AOC=180°－2∠ACO.

(2)要证明AC2=AB·AD，即证，联结BC，只需证明 Rt△ACD∽Rt△ABC.

探究2如图3，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D.

(1)求证：CD是⊙O切线;

(2)若⊙O的直径为4，AD=3，求∠BAC的度数.

分析(1)同“变形1中的探究1”.

(2)联结BC，在Rt△ABC中要求∠BAC的度数，因为AB=4，所以只需求出AC长，又已知AD=3，因此可通过Rt△ADC∽Rt△ACB来求解.

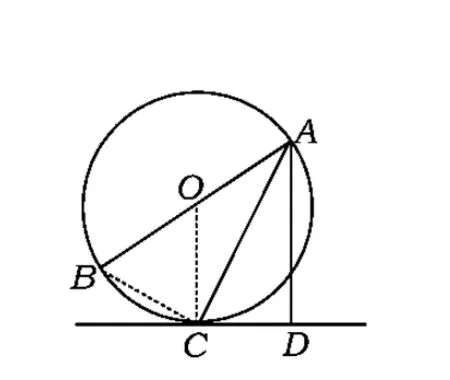
图3

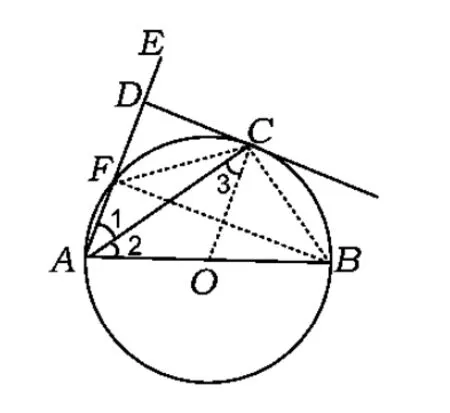
图4

探究3如图4，AB是⊙O的直径，AE交⊙O于点F，且与⊙O的切线CD互相垂直，垂足为点D.

(1)求证：∠EAC=∠CAB.

(2)若 AD=8，CD=4，①求⊙O 半径;②求tan∠BAE的值.

分析(1)同母题的解法.

(2)①联结 BC，要求⊙O的半径，只需证Rt△ACD∽Rt△ABC，由相似三角形的对应边成比例，即可求得AB的长，继而可得半径.

②联结CF与BF，要求tan∠BAE的值，只需求出AF，BF，为此需证明△DCF∽△DAC.

在母题背景下，不断探寻图形中有关边、角乃至三角形间的数量关系或位置关系，通过分析学会在复杂图形中寻找基本图形，善于挖掘出条件中的隐含信息.当赋予边或角一定的数值时，又把一般转化为特殊，形成对基本知识点的再次理解巩固，提升了数学能力!

由上述变形探索，我们会发现许多中考题都来源于教材，因此，在中考数学复习中，要依标扣本，抓基础，保能力，要重视教材中的例题及习题的再研究、再加工，进行“一题多变”的探索和练习.通过适当的延伸和拓展，分析并比较它们的异同点，加深对本质特征的认识，从而更有效地抓住问题的实质，形成正确的观点，更深刻地理解所学知识.通过精选的问题，精讲精练，沟通各部分知识间的联系，有效的形成知识网络，拓宽解题思路，培养数学思维品质，发展数学思维能力，在最终的复习过程中“以少胜多，以不变应万变”，取得最佳的复习效果.