解决一类抛物线切线问题的策略与困因分析

●赵银仓 (东莞中学 广东东莞 523000)

解决一类抛物线切线问题的策略与困因分析

●赵银仓 (东莞中学 广东东莞 523000)

圆锥曲线是解析几何的重要内容之一，尤其是直线与圆锥曲线的位置关系能综合体现解析几何的基本思想，即几何问题代数化.用代数方法来研究几何问题、用代数推算代替几何推理的数学思想，特别是直线与抛物线的位置关系问题，由于可以应用导数去分析相切关系，形成了许多交汇问题，增强了问题的综合性，提高了问题的开放度，拓宽了问题探究的思路，因而也成为高考数学命题关注的热点之一.下面一类问题就是其中的典型示例，均为高考的压轴问题(后2个题目)，解决问题的综合能力要求较高，学生解决此类问题时疑惑较多，困难较大.探究此类问题解决的通法策略，发现学生在问题解决中存在的困难，有利于指导学生解决同类问题.

1 问题展示

例1已知抛物线C的顶点为原点，其焦点F(0，c)(c＞0)到直线 l：x－y－2=0 的距离为设P为直线l上的点，过点P作抛物线C的2条切线 PA，PB，其中 A，B 为切点.

(1)求抛物线C的方程;

(2)当点P(x0，y0)为直线l上的定点时，求直线AB的方程;

(3)当点P在直线l上移动时，求|AF|·|BF|的最小值.

(2013年广东省数学高考理科试题第20题)

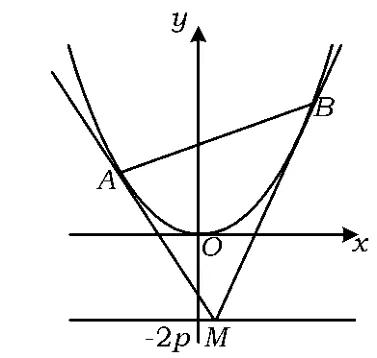
图1

例2如图1，设抛物线方程为x2=2py(p＞0)，M 为直线y=－2p上任意一点，过点M引抛物线的2条切线，切点分别为 A，B.

(1)求证：点 A，M，B 的横坐标成等差数列.

(3)是否存在点M，使得点C关于直线AB的对称点D在抛物线x2=2py(p＞0)上，其中点C满(O 为坐标原点).若存在，求出所有适合题意的点M的坐标;若不存在，请说明理由.

(2008年山东省数学高考理科试题第22题)

此类问题主要考查直线、抛物线、曲线的切线等基础知识，考查数形结合、函数与方程、化归与转化的数学思想方法，以及推理论证能力、运算求解能力和创新意识.

2 通法分析

比较这2道高考试题，可以看出它们的共同特征：(1)已知条件相似：给定抛物线C：x2=2py及一条直线l，二者相离;过直线一点引抛物线的2条切线，切点分别为A，B.(2)研究问题相近：与切点弦所在的直线有关.查阅高考试题及有关高中数学资料，可以找到很多相似的问题，研究过圆锥曲线外一点引曲线的2条切线，求切点弦所在直线的方程或探究与2个切点的弦长有关的问题.由于抛物线方程可以看作为函数的表达式，因而研究的思路更加宽阔，在高考试题中频频出现.

求抛物线切点弦所在直线方程的常见通法是：(1)根据导数的几何意义.设出切点坐标，用导数表示切线的斜率写出切线方程，利用已知点在切线上来展开思路.(2)联立方程研究位置关系.利用已知设出切线方程，联立切线方程与抛物线方程，利用判别式为0展开思路.(3)待定所求直线方程，通常用斜截式.联立直线方程与抛物线方程，用韦达定理列出切点坐标，再利用导数的几何意义列式消参求出所待定的系数.用导数求切线的斜率和联立方程研究直线与抛物线的位置关系均为课标的要求，在人教A版教材中的例、习题中都有相应的题目.下面以问题1为例进行解题策略探究.

3 解题策略

例1第(1)小题由点到直线的距离公式易得c=1，因而抛物线C的方程为x2=4y.问题的难点在第(2)小题，信息点多，涉及变量多，消参难度大.第(3)小题可以应用第(2)小题的结论，也可独立求解.

3.1 探究第(2)小题的解题策略

策略1从导数的几何意义入手，用直线与方程的关系来判断

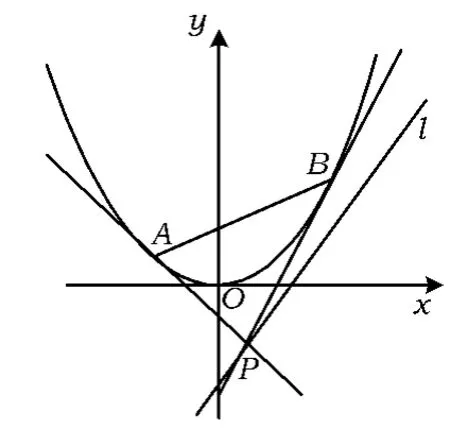
图2

解法 1如图 2，设A(x1，y1)，B(x2，y2)(x1≠x2)，因为 x2=4y，即 y=，从而切线PA的方程为

综合式(1)和式(2)得，点 A(x1，y1)，B(x2，y2)的坐标都满足方程

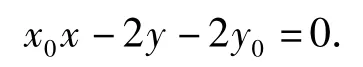
因为经过A，B的直线是唯一的，所以直线AB的方程为 x0x－2y－2y0=0.

评析解法1利用导数的几何意义并类比推理，快速地求出2条切线方程，由2条切线过同一个点发现，坐标适合同一直线方程，用直线与方程的关系判定可得直线方程.此题对导数的几何意义、推理能力与直线方程概念的理解要求较高.

策略2从待定切线方程入手，通过联立方程来判定位置关系求解

解法 2设 A(x1，y1)，B(x2，y2)(x1≠x2)，切线PA，PB的斜率分别为k1，k2，则切线方程可统一设为

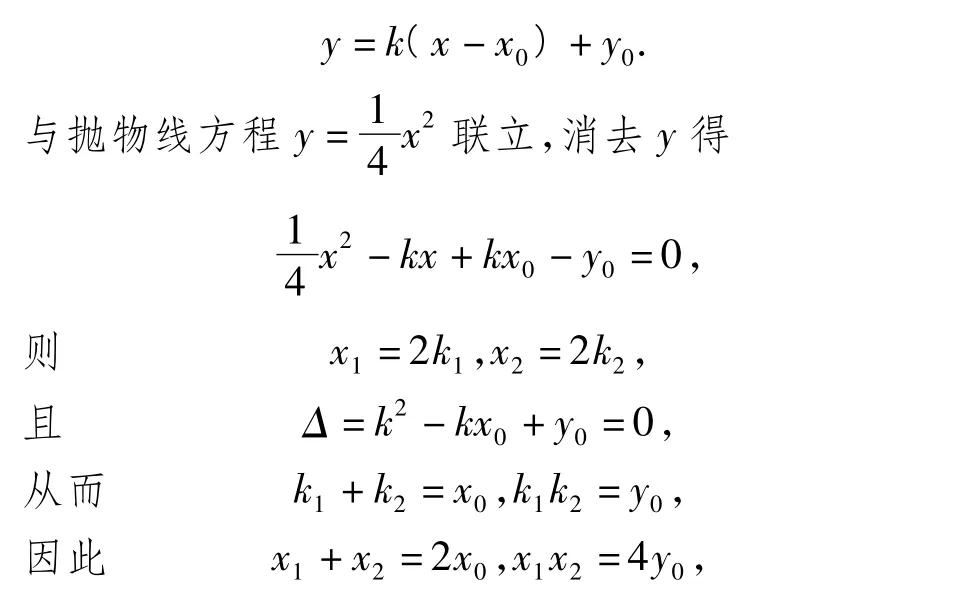
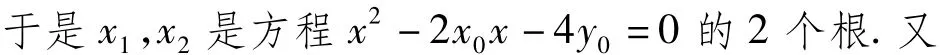
评析待定切线方程，联立方程用解的情况来研究也是一种通法，联立方程利用相切判别式为0得到切线的斜率所满足的关系及方程的唯一解.解法2从根与系数的关系入手并结合直线方程的意义得解;解法3则利用直线的点斜式方程求解，参数多，运算能力要求高.

策略3从待定直线AB的方程入手，利用点A，B处的切线来确定参数

解法 4设 A(x1，y1)，B(x2，y2)(x1≠x2)，由于直线AB的斜率存在，故可设其方程为

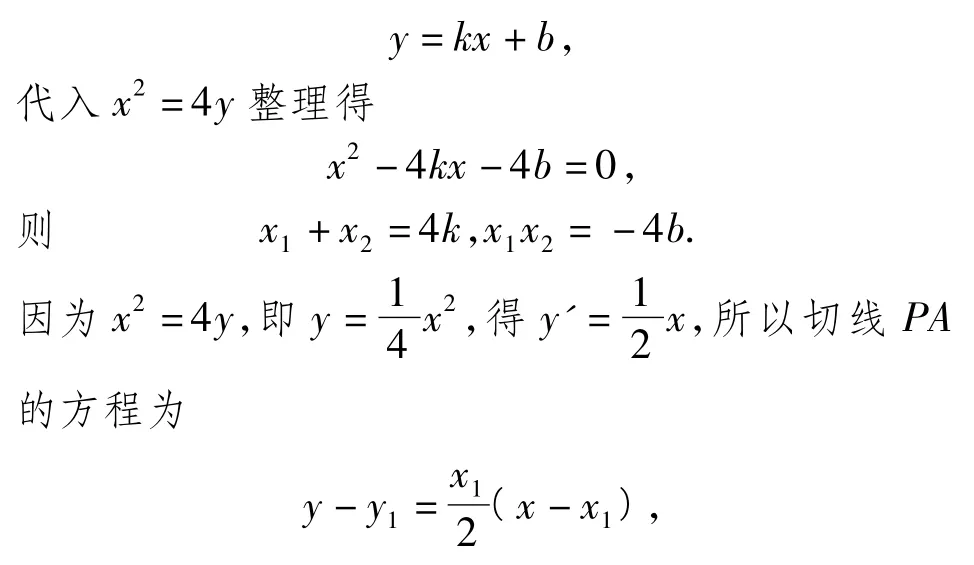
评析待定直线的斜截式方程，联立方程由根与系数的关系，结合导数得到斜率和截距与坐标之间的表示式，这也是通法.

评析用切点坐标为参数来表示直线方程，解法5结合导数整体消参得到斜率和截距.而解法6在消参时得到了切点坐标之间的一个关系，给下一小题的解决带来了便利.此题关系复杂，要求学生的推理能力高，对问题的驾驭能力强.

3.2 探究第(3)小题的求解策略

策略1用切点坐标为变量，换元构造函数

解法1由第(2)小题的解答过程知

评析以坐标为变量既与前一小题相通，也容易写出函数表达式，利用换元法化为熟悉的二次函数，避免了联立方程使用韦达定理，符合课标的要求.解法2中向量的使用，除去了对前一小题过程的依赖.

策略2以已知动点坐标为变量，通过联立方程确定函数

评析注意到切点A，B由点P所确定，选择点P的坐标为变量，则点A，B的坐标可以通过联立方程来确定，使用韦达定理实现设而不求.其中解法3用定义转化，思路简明，解法4直接用距离公式化归，殊途同归.

策略3以直线AB斜率为变量，利用联立方程化归函数

评析考虑到直线AB过定点(2，2)这一事实，若设其斜率为变量，则过程更简洁.

4 困因分析

例3过点A(2，3)的直线l与抛物线C2：x2=4y交于点B，C，抛物线C2在点B，C处的切线分别为l1，l2，且l1与l2交于点P，求动点P的轨迹.

该题是2013年广州市数学高考模拟考试理科第20题的关键部分，显然例1的第(2)小题是其逆命题，也是这道题的难点，解法基本一致.例3作为诊断性考试的一道试题，旨在了解复习备考情况，反馈信息，指导教学.笔者所在东莞市参加了这次考试并组织了统一阅卷，从全市统计数据来看，该题的得分率仅为0.23，A类学校的得分率也只有0.33.答卷中暴露出学生存在着很多疑惑与困难，在解题中存在着不少问题.

4.1 在具体的问题情境中，不会应用导数的几何意义

导数是解决函数问题的重要工具，导数的几何意义使得求曲线的切线方程十分便捷.应用导数求切线方程要准确理解其几何意义：函数y=f(x)在x=x0处的导数就是其图像在对应点处的切线的斜率.就该题来说，由于题目给出的是抛物线方程，也就是曲线的方程，要将其变为相应的函数形式才能求导;用导数求切线的斜率必须设出切点坐标.正是由于对这2点认识不到位，不少学生不能写出切线方程.

4.2 对直线与方程之间关系本质涵义不理解，因而不能从数学意义上分析问题

解析几何是用代数方法研究几何问题，需将几何问题化为代数问题.但这2个问题之间必须能建立起一一对应关系，就是通过曲线上的点与方程的解之间的对应使二者结合起来.由于直线有其特殊性，2个点确定且只确定一条直线，因此直线上只要有2个点适合一个二元一次方程，则此方程必表示该直线的方程.这个原理虽然并不难理解，但已经触及直线与方程关系的本质涵义，学生平时练习中只重视求直线的方法，重视数学推算，很少在推理运算过程中，从数学意义的角度审视推算、运算结果，把握其本质.因而在解答该题时，不能由2条切线方程形式的一致性判断出切点弦所在直线的方程，在运算中徘徊.

4.3 没有养成用数学思想指导、分析问题的习惯

这类问题的典型特征是变量参数多、关系式复杂，容易使学生迷失方向，看到很多式子不知如何推算.而产生这种问题的原因是没有用数学思想去指导分析问题，没有从整体上对解题进行规划，明确解题的方向路线.如在例1的解答中，涉及到6个以上参变量，如果用整体思想、对称思想、方程思想去指导分析，就会明确设众多参数的目的是沟通切线与切点弦之间的联系，但最终目标是求出切点弦所在直线方程的系数，或直接推理得出方程.因而解题思路是围绕如何选择有效途径消参来展开，推算则不再盲目.整体思想与对称思想的应用使解题过程简化.

4.4 运算推理能力弱是解题的最大瓶颈

面对解析几何问题，学生感觉最大的困惑是涉及多参的情况下，参数的处理能力弱，运算推理能力不强.不少学生解题思路能够形成，但是在实施解题方案的过程中，往往是列出了参量之间的关系式但不知怎么处理，后续运算难以为继，因而解题活动被迫中断;还有一种情形是在某一环节运算出现差错，没有养成对过程反思与检查的习惯，而是不停地推算，从而离问题解决越来越远.前者为推理思路不明，后者为运算能力不强.可见“推算”的功夫不够是解题的最大瓶颈.如例1的解答中，设出切点坐标、列出切线方程及切点弦方程后，问题将聚焦在如何消去4个参数，用已知点坐标将切点弦方程表示出来.由于运算能力的制约，面对众多的参数，大多学生感觉到束手无策.

［1］ 赵银仓.解析几何中一类典型错解的分析［J］.中国数学教育：高中版.2012(9)：34-36.

［2］赵银仓.从高考答卷的错误反思教学的缺失［J］.数学通讯：教师.2013(7)：46-50.

［3］ 曹才翰，章建跃.数学教育心理学［M］.北京：北京师范大学出版社.2006：186-195.