玻璃转变时非晶合金微观结构演变的新进展*
陈 清,范 沧, 梁 兵
(1.湖南大学 材料科学与工程学院, 湖南 长沙 410082;2.南京理工大学 材料科学与工程学院, 江苏 南京 210094;3.国防科学技术大学, 指挥军官基础教育学院, 湖南 长沙 410073)
非晶合金,又称金属玻璃,因其具有独特的物理、化学和力学性能,一直是材料科学与工程技术领域的研究重点之一[1,2].非晶合金不具有长程有序性和单胞结构,其原子结构非常复杂,目前对金属玻璃的原子排列问题还在不断的探讨中.另外,由于目前没有一种足够合理的原子模型,因此金属玻璃许多独特的力学、物理性能还不能通过其原子结构进行很好的解释.
玻璃转变是非晶材料一个非常关键的现象.被加热时,非晶在玻璃转变温度(Tg)时转变为过冷液态.在这个转变过程中,材料的内能变化极小,但物理、力学性能的变化却很显著[1-6].以往对玻璃转变现象的研究集中在分子基玻璃材料,且一般从动力学和热力学角度出发进行研究[3,5,7,8],但很少有人研究非晶的原子结构.自从非晶合金于1960年通过急冷的方法被首次合成以来[9],制备非晶合金需要高达105K/s的冷却速度.现在,只需将液态合金以100至102K/s的冷却速度冷却下来,就能成功获得大块金属玻璃[1,2,10,11].这些大块金属玻璃是研究玻璃转变现象极好的材料.本论文以Zr-Cu-Al金属玻璃为研究对象,研究在玻璃转变过程中原子级热膨胀的变化,自由体积的演变及其与金属玻璃原子排列模型的关系[12,13].
1 实验过程
在实验中,通过原子对分布函数(Pair distribution function, 简称为PDF)来分析大块金属玻璃Zr55Cu35Al10(at.%)的局域原子结构.Zr55Cu35Al10母合金由高纯度的锆、铜、铝按原子百分比混合,在铜冷型真空电弧熔炼炉中抽真空,而后在氩气的保护下进行熔炼.利用真空吸铸铜型冷却方法将熔炼的母合金制备成1 mm厚的板状非晶合金试样和直径为3 mm,长约50 mm的棒状非晶合金试样.板状试样用于同步辐射实验,棒状试样用于中子衍射实验.由差热扫描分析仪(DSC)测定非晶合金试样的玻璃转变温度(Tg)为420 ℃,结晶化温度Tx为492 ℃,实验时DSC的加热速度为20 ℃/min.注意到Tg与Tx之间存在显著的差别,因此可以在较大的温度范围内通过原位同步辐射X射线衍射观察玻璃转变时的原子结构演变,而无需担心试样结晶化.
在原位同步辐射X射线衍射实验中,试样被加热的速度约为20℃/min,该实验在美国阿贡国家实验室的强光子源11-D光束线上进行.另外还对铸态和结晶化后的试样进行中子衍射实验,以获得相应状态下的对分布函数,该实验在美国洛斯阿拉莫斯国家实验室Lujan中子散射中心的中子粉末衍射仪上进行.原位同步辐射X射线衍射实验的示意图如图1所示[12].入射光子通过被加热的试样被图像探测器记录下来形成2维图像.

图1 原位同步辐射X射线衍射实验中控制试样温度的加热装置示意图,以及图像探测器记录的2维图像
在收集衍射数据I(Q)时,Q的范围很宽(>30 Å-1,Q=(4πsinθ)/λ,θ为衍射角,λ为X射线波长).随后,分别使用PDFgetX2软件[14]和PDFgetN软件[15]对X射线衍射数据和中子衍射数据进行处理, 即对Q[S(Q)-1]进行傅里叶变换(S(Q)为结构函数),最终得到对分布函数G(r),r为原子对中两原子间的距离:
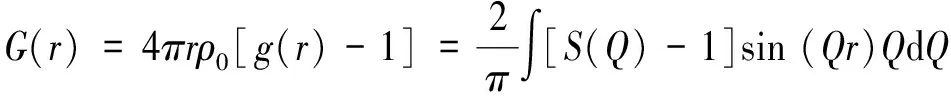
(1)
2 实验结果
为了研究试样在玻璃转变过程中局域原子结构随温度的升高而发生的演变,尤其是原子级的热膨胀,对铸态Zr55Cu35Al10大块金属玻璃进行原位同步辐射X射线衍射实验时选取的温度区间为室温到450 ℃,比试样的结晶化温度Tx(492 ℃)低了很多,因此试样在实验过程中不会结晶化.图2(a)和(b)所示分别为室温和450 ℃时的结构函数S(Q)和对分布函数G(r),在不同温度下的曲线差别小得几乎观察不到,这说明试样在实验过程中,在不同温度下均保持在非晶态.

Q/(Angstrom-1)

r/(Angstrom)
如果将对分布函数放大,只观察最近邻原子的对函数,可以得到随温度变化的原子间的细微变化.图3(a)所示为最近邻原子对的对分布函数(对分布函数的第一峰).从图上可以看到温度为450 ℃时曲线的峰强较室温时的峰强要小,但峰宽比室温时要大.结晶化对对分布函数所产生的影响更大,如图3(b)所示,此图是由室温下的中子衍射实验获得的.其中的结晶化试样在约700 ℃下退火3 h以获得稳定的晶相.与非晶试样的对分布函数相比,结晶化后的试样其对分布函数的峰宽变窄很多,强度更是明显增加.值得注意的是,由于同步辐射X射线衍射和中子衍射实验不一样,因此图3(a)和(b)中同一个非晶合金试样的对分布函数的强度不一样[12].

r/Å

r/Å
图3 Zr55Cu35Al10最近邻原子对分布函数(a)为温度为室温和450 ℃时对试样进行原位同步辐射X射线衍射实验获得的;(b)为室温下对铸态试样和结晶化后的试样(在约700 ℃下退火1 800 s)进行中子散射实验获得的
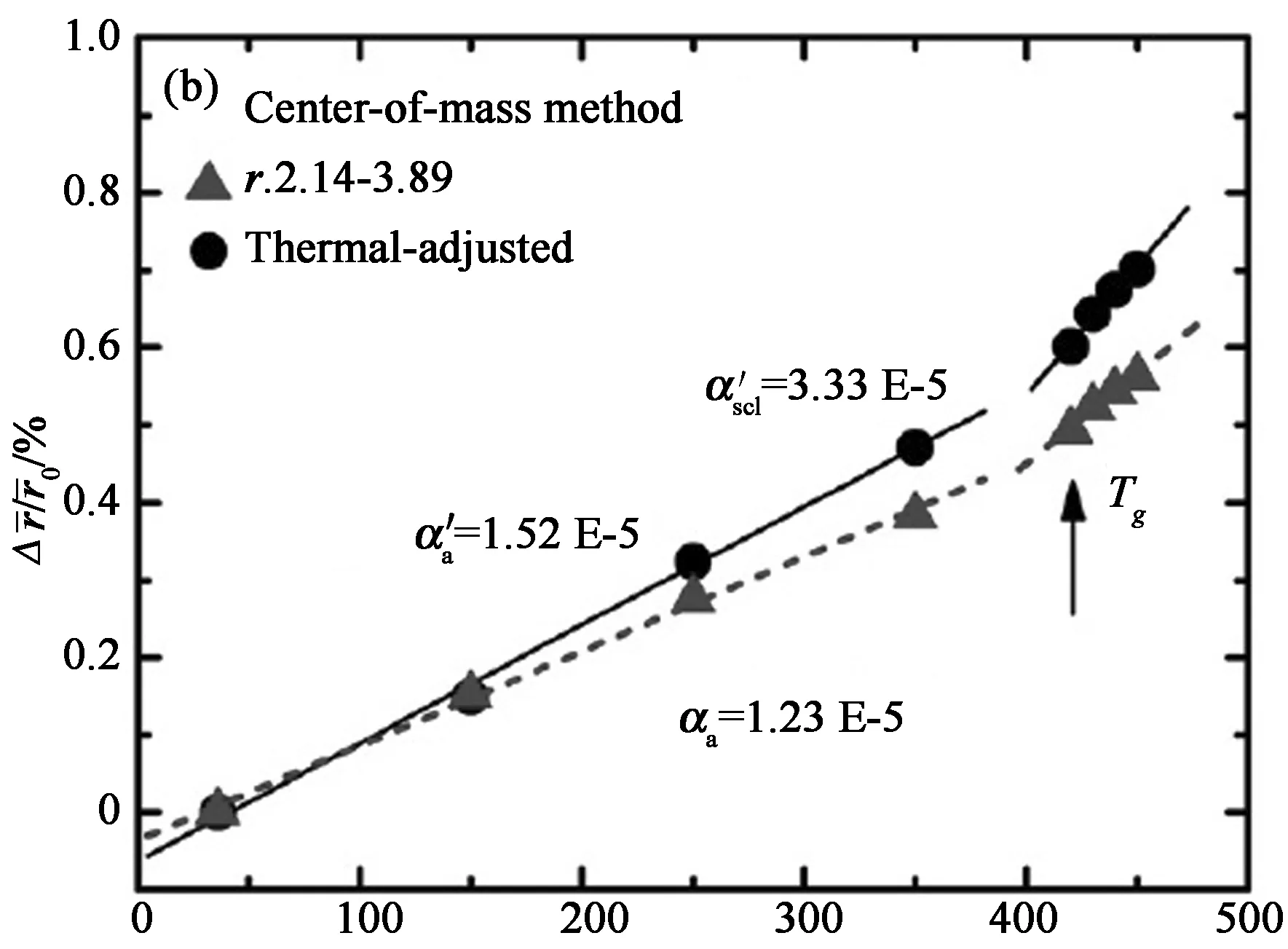
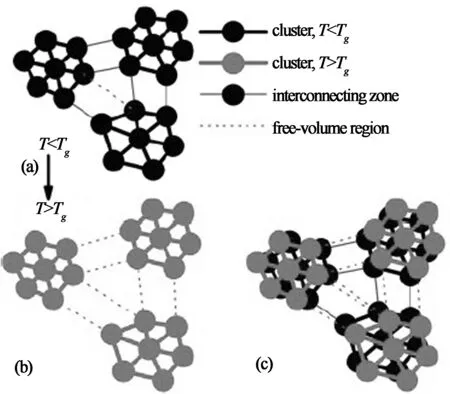
Fig.3 The nearest neighbor peaks of the reduced PDFs of Zr55Cu35Al10: (a) in situ measured by synchrotron x-ray scattering at RT and at 450 ℃(Tg 径向分布函数包含更多的最近邻原子之间的数量关系.通过对分布函数,可以简单地得到径向分布函数 (Radial Distribution Function,RDF): R(r)=4πr2ρ0g(r)=rG(r)+4πr2ρ0 (2) 式中的R(r)dr表示与中心原子距离为r,厚度为dr的环中所含原子的数量.因此,可以对径向分布函数R(r)进行进一步的计算分析.图4中所示的是选择最近邻原子对的径向分布函数的不同区域进行放大后的图像. 上文中提到的对分布函数随温度的变化,即450 ℃时曲线的峰强较室温时的峰强要小,但峰宽比室温时要大,在图4中更为明显[13].当试样开始结晶化后,峰强随温度升高而增加而峰宽减小,如图4中的虚线所示. (3) r/Å r/Å 当温度高于Tg时,如图5(b)的黑色实线所示,即温度在420 ℃至450℃范围内的斜率从单一热膨胀之前的1.52×10-5K-1变至3.33×10-5K-1,增加了约50%(在没有进行自洽调整的数据中,斜率从1.23×10-5K-1变至2.3×10-5K-1,也增加了50%,如图中的虚线所示).温度超过Tg后斜率的增加,表明玻璃转变后的过冷液体有额外的体积膨胀,这是由于在玻璃转变过程中原子的堆垛结构发生了变化. 为了进一步表征径向分布函数随温度的升高而产生的宽化,以研究玻璃转变过程中的原子结构的变化,通过式(4)计算径向分布函数第一峰r1至r2区域内的原子对的数量. (4) 如图3(a)所示,当r1=3.55 Å,r2=3.89 Å时,N代表的是与3.24 Å相比原子间距较长的原子对数量,这里3.24 Å是最近邻的Zr-Zr原子对在晶体结构时的原子间距. 即使上述临界值在一定程度上是任意选取在10%左右,对结果也不会产生影响,因为本文感兴趣的是▽N/N0相对变化量,其中▽N=N(T)-N0;N0是室温下原子间距在r1至r2区域内原子对数量.图6(a)所示为由径向分布函数计算得到的r在3.55 Å至3.89 Å区间的▽N/N0.温度大于Tg时△N/N0的斜率(Bscl=9.7×10-2)是温度小于Tg时(Ba=4.0×10-2)的2倍以上,斜率的增加十分显著.△N的物理意义为移进与移出r1至r2区域的原子数量之差,如图6(b)所示.而Bsc/Ba= 2.4表示温度在Tg以上时进入r1至r2区域的原子数是温度在Tg以下的2.4倍. r/Å Temperature,T/℃ Temperature/℃ 图6 (a) 由径向分布函数第一峰计算得到的△N/N0值随温度的变化函数,其中,△N=N(T)-N0,N为3.55 Å至3.89 Å范围内径向分布函数下的面积,N0是室温下的值;(b)当温度变化时移进和移出r1至r2区域的原子对示意图 Fig.6 (a) Changes in the areas of the first peak of the RDF, △N/N0, as a function of temperature, where △N=N(T)-N0,N: the area of the RDF first peak from 3.55 Å to 3.89 Å,N0: the value at room temperature. (b) Illustration of atom pairs moving in and out of ther1tor2range when the temperature changes[12] 在自由体积理论中,类液态结构区域被定义为大量的过剩自由体积[17,19].自由体积理论被广泛地应用到金属玻璃领域[16],但其提出者却反对其在金属领域内的应用,因为自由体积的临界值γv*/v0仅为0.1,其中v0为原子的体积,然而在硬球模型中此临界值为0.8,且自由体积理论就是为硬球模型而提出的.事实上,金属原子并不是硬球,而是很容易变形,因此很难适用原始的自由体积理论[20-22].为此,近些年来研究工作者对自由体积的概念在做进一步的研究.自由体积可以定义为低于平均局域原子密度的区域.在金属玻璃中,局域原子体积的分布是很协调的,非常接近于高斯分布[23],从低于到高于平均局域原子密度的区域均存在,在基于原子应力的理论中,低于平均局域原子密度的区域称为自由体积或n型缺陷,而高于平均局域原子密度的区域称为反自由体积或p型缺陷.这样可以定量地推导出判断局域结构稳定性的临界值,即临界局域体积应变εv=0.11[18],如图7所示.对于体积应力大于临界值的结构不稳定区域,当其密度超过相互渗透的极限时,将发生玻璃转变,由此可以计算出许多金属玻璃的Tg,并且计算值与测量值吻合得很好[18]. Volume Strain 图7 局域原子体积分布.灰色区域表示结构不稳定的位置,其体积应变大于±0.11. 当温度上升时,该分布曲线将变宽,导致更多的位置处于结构不稳定的区域.当这些位置的密度达到相互渗透的极限时,即发生玻璃转变[13] Fig.7 Distribution of local atomic volume. Gray zones indicate topologically unstable sites with the volume strain greater than ±0.11. As temperature is increased the distribution becomes wider, resulting in more and more sites with the unstable local structure. The glass transition occurs when the density of such sites reaches the percolation limit[13] 图3(b)表明一些原子对的键长明显要比退火后的试样中的原子对要短,这个特征说明大块金属玻璃中的团簇由超常短键的原子对组成.图3(b)还表明有一些原子对的键长明显要比结晶化后试样中的原子对要长,这个特征又说明大块金属玻璃中还存在相当数量的自由体积.这些包含超常短键的团簇和由弱结合原子对形成的自由体积在大块金属玻璃中和谐共存.因此,基于Lindemann熔化准则,有理由认为当原子对距离大于3.55 Å (图6中的r1),小于3.89 Å (r2, 最近邻原子对的最大值)时为自由体积区域,上文已提到3.55 Å大于原子尺寸最大的Zr-Zr原子对距离,3.24 Å的10%. 差热扫描分析(DSC)实验测得在玻璃转变过程中所吸收的能量为0.79 W/g,在结晶化过程中所释放的能量为14.3 W/g. 然而,玻璃转变过程中吸收如此少的能量却能够使物理、机械性能发生很大的变化,例如Zr基大块金属玻璃在发生玻璃转变后,其屈服强度从约2 000 MPa降至约70 MPa. 玻璃转变过程中如此小的能量是如何改变原子的结构,从而导致物理、机械性能的变化呢? 一些键长比r1短的原子对,在升温过程中其键长不断增加从而进入r1至r2之间的区域.而一些键长在r1至r2之间的原子对,在升温过程中其键长不断增加到大于r2的区域,从而移出r1至r2的区间,如图6(b)所示.进入r1至r2区域的原子对多于流出此区间的原子对时,导致自由体积的增加.由图6(a)所示,当温度高于Tg时,△N/N0增加得更为显著,增加到原来的2.4倍(Bscl/Ba=0.097/0.04).这也表明温度高于Tg时,随温度的增加,自由体积的增加率提高了2.4倍. 基于以上的讨论,吸收较少的能量就能形成较多的自由体积,并且随着自由体积的增加,含超常短键的团簇就被自由体积形成的结构网络分割开,此时非晶态就完全转变为过冷态,如图8所示.团簇与团簇之间的固态连接区域在玻璃转变的吸热过程中不断膨胀,这些固态连接区被定义为过渡区.根据过渡区概念建立的非晶的原子结构模型可以描述为:由过渡区链接含超常短键团簇的过渡区团簇模型[12].该模型认为金属玻璃中存在三种原子结构(区域):1)由强化学键紧密连接的原子团簇(cluster).原子团簇区域内含有较晶体结合键更短的超短键原子结合,构成原子的压缩区域.原子团簇内结合强度较大;2)团簇之间的自由体积,这个区域的原子间键长较长,呈液态结合性质,结合强度较弱;3)连接团簇的过渡区,这个区域的原子间键长短于自由体积的原子间的键长,但大于原子对在相应晶体中的键长,结合强度也介于团簇原子和自由体积区域原子之间的结合强度. 根据此过渡区团簇模型,可以对玻璃转变进行更深入的理解,如图8所示. 图8 玻璃转变过程中原子结构的示意图:低于或超过Tg时团簇之间的连接变化(黑色代表温度低于Tg,红色代表温度高于Tg) Fig.8 (a)-(c) Schematic showing the structural change at the glass transition: a change in the connections between clusters below and aboveTg(black: belowTgand red: aboveTg)[12] 通过原位同步辐射X射线原子对分布函数对金属玻璃的局域原子结构进行了研究,得到了升温时局域原子结构的两个演变特征:原子级的微观热膨胀是宏观热膨胀的一半,其可能的原因是低于玻璃转变温度时存在类液体的局域原子结构,并导致热膨胀的增加;原子对分布函数随温度的变化与局域原子密度的玻璃一致,自由体积随着温度的升高而增加,且温度超过Tg时,自由体积增加得更快,自由体积形成一个网络将含超常短键的团簇隔开是玻璃转变的物理机制.另外,基于上述对玻璃转变过程原子结构演变的研究,提出了一种含超常短键的团簇模型,该模型能够很好地解释从高屈服强度的非晶态到低屈服强度的过冷液态的玻璃转变,以及玻璃转变过程中有限的塑性变形能力到超塑性变形能力的变化. [1]INOUE A. Bulk amorphous alloys: preparation and functional characteristics [M]. Switzerland: Transactions of Technology Publications, 1998. [2]JOHNSON W L. Metastable phases [M]. New York: Wiley, 1994: 687. [3]DEBENEDETTI P G, STILLINGER F H. Supercooled liquids and the glass transition [J]. Nature, 2001, 410(6825): 259-267. [4]HIGHMORE R J, GREER A L. Eutectics and the formation of amorphous-alloy [J]. Nature, 1989, 339(6223): 363-365. [5]EDIGER M D. Supercooled liquids and glasses [J]. Journal of Physical Chemistry, 1996, 100(31): 13200-13212. [6]LEE K S, HAB T K, AHNB S,etal. High temperature deformation behavior of the Zr41.2Ti13.8Cu12.5Ni10Be22.5bulk metallic glass [J]. Journal of Non-Crystalline Solids, 2003, 317: 193-199. [7]MISHIMA O, EUGENE S H. The relationship between liquid, supercooled and glassy water [J]. Nature, 1998, 396: 329-335. [8]SASTRY S, DEBENEDETTI P G, STILLINGER F H. Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid [J]. Nature, 1998, 393: 554-557. [9]KLEMENT W, WILLENS R, DUWEZ P. Non-crystalline structure in solidified gold-silicon alloys [J]. Nature, 1960, 187: 869-870. [10]PONNAMBALAM V, POON S J, SHIFLET G J. Fe-based bulk metallic glasses with diameter thickness larger than one centimeter [J]. Journal of Materials Research, 2004, 19(5): 1320-1323. [11]MA H, MA E, XU J. A new Mg65Cu7.5Ni7.5Zn5Ag5Y10bulk metallic glass with strong glass-forming ability [J]. Journal of Materials Research, 2003, 18(10): 2288-2291. [12]FAN C,REN Y,LIU C T,etal. Atomic migration and bonding characteristics during a glass transition investigated using as-cast Zr-Cu-Al[J]. Phys Rev B, 2011, 83: 195207. [13]FAN C, YAN H G, LIU C T,etal. Changes in the atomic structure through glass transition observed by X-ray scattering[J]. Intermetallics, 2012, 23, 111-115. [14]QIU X Y, BOZIN E S, JUHAS P,etal. Reciprocal-space instrumental effects on the real-space neutron atomic pair distribution function [J]. Journal of Applied Crystallography, 2004,37: 110-116. [15]PETERSON P F, GUTMANN M, PROFFEN T,etal. A user-friendly program to extract the total scattering structure function and the pair distribution function from neutron powder diffraction data [J]. Journal of Applied Crystallography, 2000, 33: 1192. [16]COHEN M H, GREST G S. Liquid-glass transition, a free-volume approach [J]. Physical Review B, 1979, 20(3): 1077-1098. [17]EGAMI T, POON S J, ZHANG Z,etal. Glass transition in metallic glasses: A microscopic model of topological fluctuations in the bonding network [J]. Physical Review B, 2007, 76(2): 024203. [18]COHEN M H, TURNBULL D. Molecular transport in liquids and glasses [J]. Journal of Chemical Physics, 1959, 31(5): 1164-1169. [19]FAN C, LIAW P K, WILSON T W,etal. Pair distribution function study and mechanical behavior of as-cast and structurally relaxed Zr-based bulk metallic glasses [J]. Applied Physics Letters, 2006, 89(23):231920. [20]FAN C, LIAW P K, WILSON T W,etal. Structural model for bulk amorphous alloys [J]. Applied Physics Letters, 2006, 89(11): 111905. [21]FAN C, LIAW P K, HAAS V,etal. Structures and mechanical behaviors of Zr55Cu35Al10 bulk amorphous alloys at ambient and cryogenic temperatures [J]. Physical Review B, 2006, 74(1): 014205. [22]SROLOVITZ D, MAEDA K, TAKEUCHI S,etal. Local-structure and topology of a model amorphous metal [J]. Journal of Physics F-Metal Physics, 1981, 11(11): 2209-2219. [23]EGAMI T, MAEDA K, VITEK V. Structural defects in amorphous solids a computer simulation study [J]. Philosophical Magazine A, 1980, 41(6): 883-901.
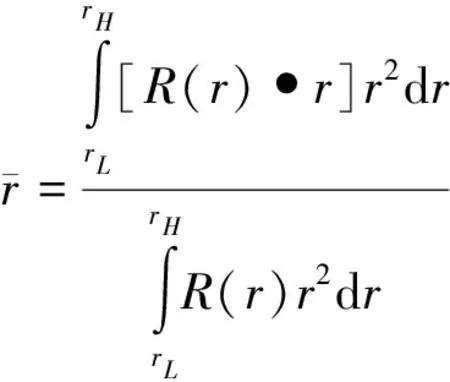



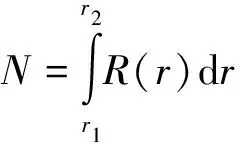


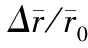
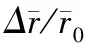

3 讨 论



4 结 论

