支柱瓷绝缘子表面裂纹应力强度因子的有限元分析*

肖汉宁，彭苏华，高朋召

(湖南大学 材料科学与工程学院, 湖南 长沙 410082)

近年来电站用高压支柱瓷绝缘子断裂事故时有发生，给电力系统正常运行及人身安全带来危害.对大量事故原因进行分析，不难发现，瓷件断裂与结构中存在的裂纹有关，而表面裂纹对瓷件强度的影响尤为突出.应力强度因子是判断含裂纹构件断裂和计算裂纹扩展速率的重要参量，而应用断裂力学来解决工程实际问题，首先需要确定裂纹尖端的应力强度因子[1-2].

随着计算机模拟技术的发展，裂纹仿真成为可能.在众多仿真方法中，有限元法以其不受裂纹体几何及载荷形式的限制而在断裂力学中得到广泛应用[3].通过有限元软件ANSYS，ABAQUS等可计算裂纹尖端应力强度因子，计算的关键在于如何构建能够反映裂纹尖端奇异应力场的裂纹模型.三维裂纹模型的建立一般有两种方法：逐节点直接建模法和实体建模法.前者虽为多数人采用，但工作繁琐且容易出错，不适合复杂结构[4].

本文针对支柱瓷绝缘子结构中常见的表面裂纹，采用实体建模法，首先对整体结构和裂纹部分分别建模，然后运用布尔运算将其分离，再对裂纹部分采用特殊的网格划分方式进行划分，最后通过施加边界条件和载荷来计算不同尺寸、位置的裂纹尖端应力强度因子.

1 有限元法求解应力强度因子基本理论

基于三维有限单元法的裂纹尖端应力强度因子计算方法主要有1/4节点位移法和三维J积分法[5]，其中J积分法计算应力强度因子的过程较为繁杂，不便于多次重复求解，本文选择1/4节点法计算裂纹尖端应力强度因子K值.根据线弹性断裂力学理论[6-8]，裂纹尖端的位移场可表示为：

(1)

(2)

ut=0．

(3)

式中：n和t分别为裂纹前沿的法线方向和切线方向；z为垂直于裂纹平面方向(见图1)；μ为材料剪切模量.

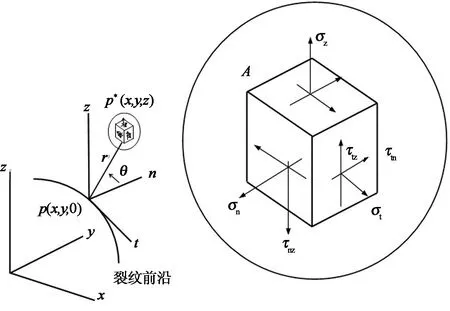
图1 曲线裂纹前缘坐标系

根据式(2)，若裂纹表面上(θ=180°)某一点的垂直于裂纹平面的位移已知，那么应力强度因子

(4)

将从有限单元法求出的1/4点位移uz(1/4)代入式(4)得

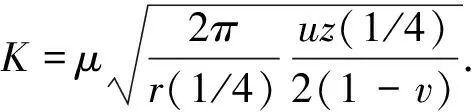
(5)

2 有限元模型的构建及计算求解

支柱瓷绝缘子一般由铸铁法兰、水泥胶合剂、瓷体三部分胶装而成，分析时假设两种材料之间完全粘牢，即两种材料接触界面不存在相对滑动.组成绝缘子的各材料特性参数值如表1所示，文中所使用的绝缘子主要尺寸参数如表2所示.

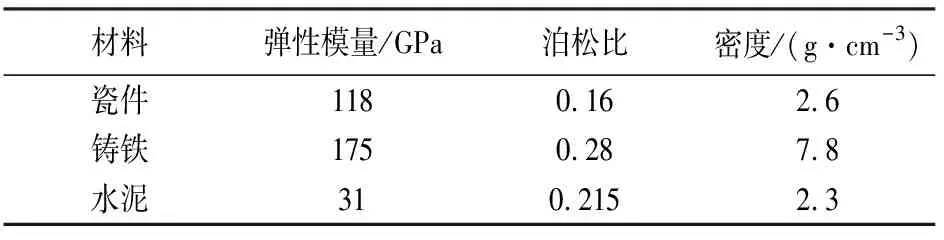
表1 瓷绝缘子组成材料的性能参数

表2 瓷绝缘子主要尺寸参数

实际工程中，裂纹是不规则的，半椭圆裂纹是表面裂纹的一种理想化形式，是仿真计算中常用的一种模型[9].本文将表面裂纹简化为半椭圆形状处理，裂纹位于支柱表面垂直于轴向，弯曲载荷作用于绝缘子上法兰处，平行于裂纹面.支柱瓷绝缘子的几何模型和裂纹横截面示意如图2，其中d1=2R；a为椭圆短半轴，即裂纹深度；b为椭圆长半轴，2b约等于裂纹长度.

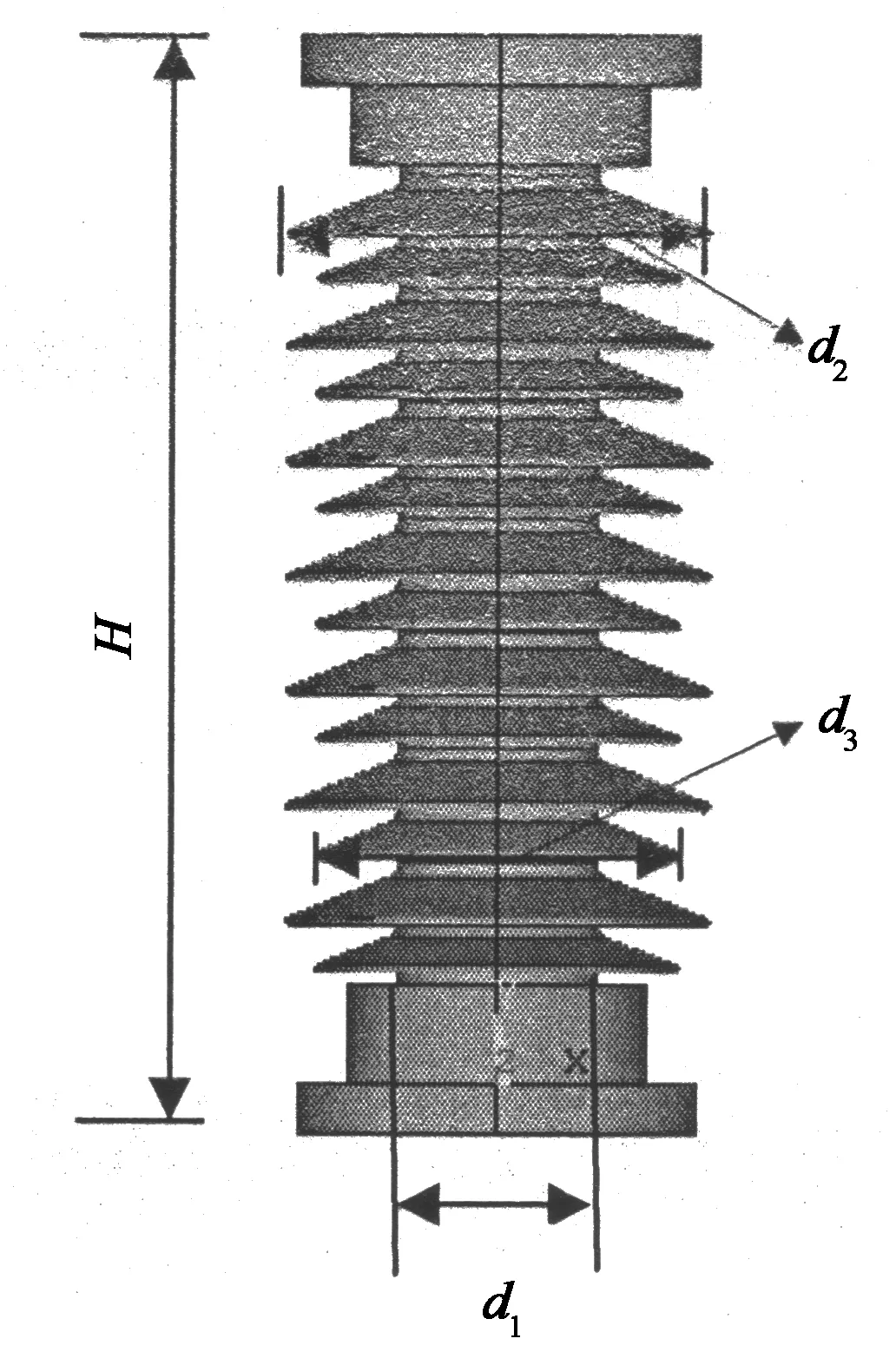
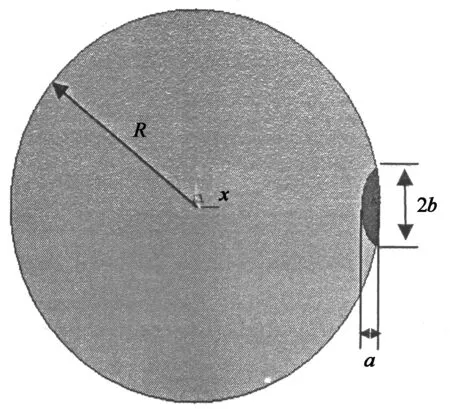
图2 瓷绝缘子几何模型及裂纹横截面说明

研究中采用“自上向下”的实体建模方法，该方法关键在于对裂纹部分进行特殊的网格划分.由于

裂纹尖端的应力和应变是奇异的，因此在进行有限元建模或单元网格划分时，必须先在裂纹尖端位置定义应变奇异点，而常规单元的位移模式不能反映尖端位移处的奇异性.Barsoum等[10]通过把裂纹尖端附近二阶单元的中间节点沿裂纹尖端方向移至靠近裂尖1/4分点处(如图3)，较准确地反映了裂尖附近应力场的奇异性.

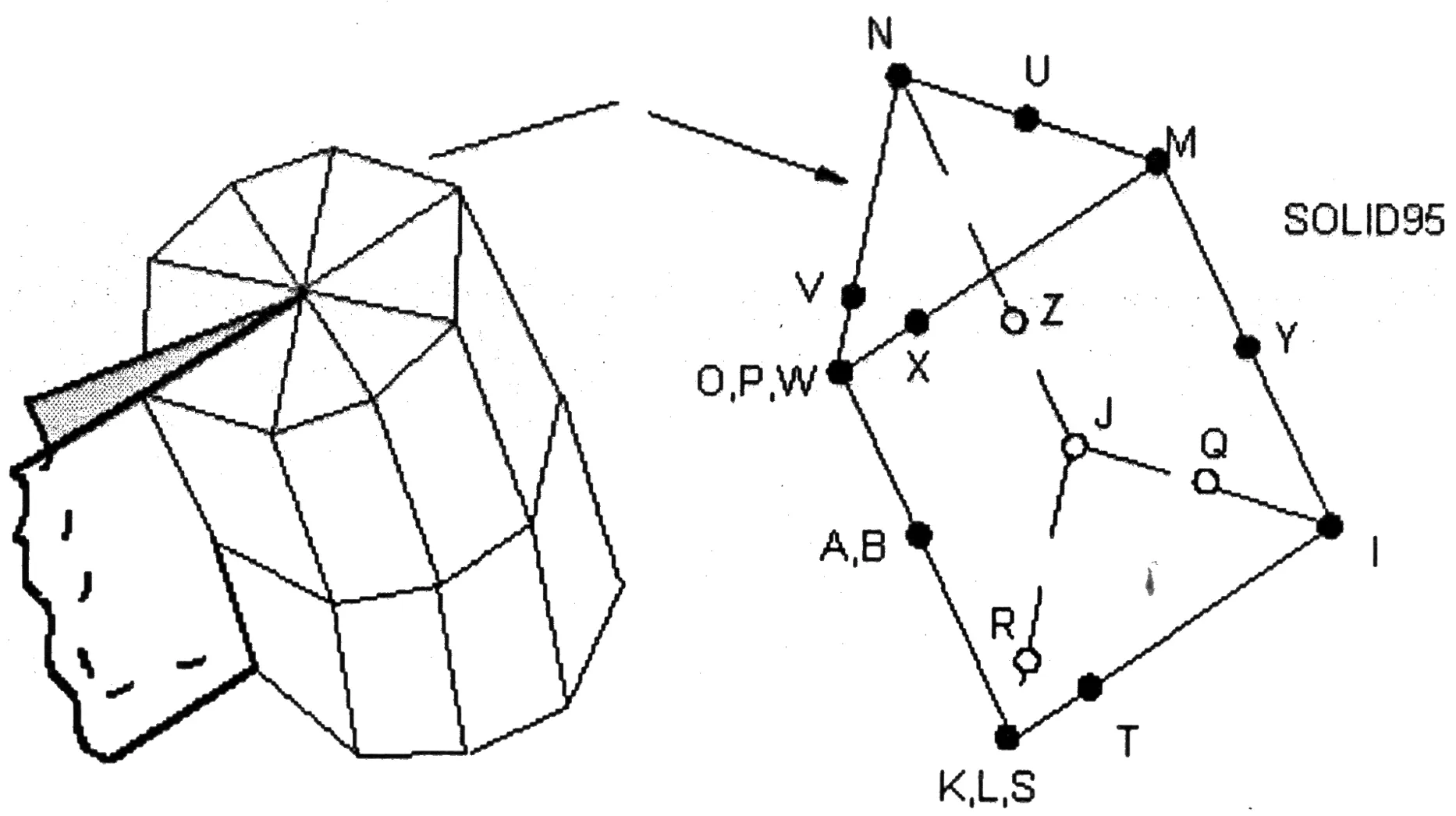
图3 裂纹前缘奇异单元及尖端附近网格构造

分析中，裂纹前缘采用20节点solid 186单元的棱柱退化形式模拟其奇异性，划分网格时首先是采用MESH200单元，通过在裂纹尖端设置奇异点来生成二维的奇异单元(图4(a))，然后将所生成的面网格沿裂纹深度方向通过体扫掠划分生成三维单元(图4(b)).对非裂纹区采用4节点solid 285单元进行网格划分，最后瓷绝缘子整体有限元模型如图4(c)所示.为了获得理想计算结果，围绕裂纹尖端单元的第一行单元半径设为1/8裂纹深度或更小，单元角度在15～30°之间.

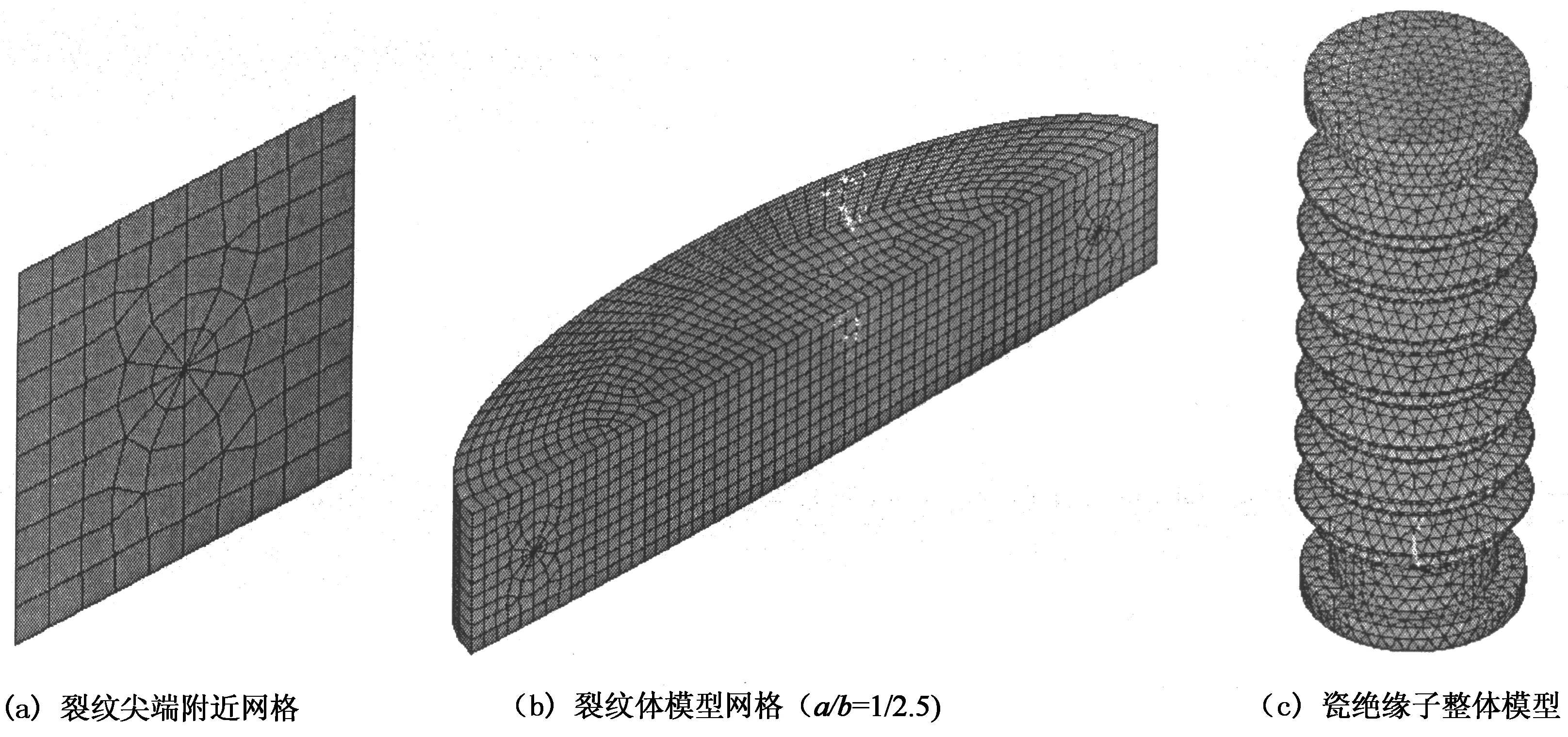
图4 裂纹体模型的生成及瓷绝缘子有限元模型

支柱瓷绝缘子的有限元模型建立后，对绝缘子底端施加位移约束，顶部施加一垂直轴向的载荷Fx，然后进行结构静力学计算.在ANSYS中，通过通用后处理器POST1的KCALC命令[11]，采用平面应变位移外推法计算应力强度因子，使用此命令前，需要定义描述裂纹尖端的局部坐标系和计算路径，坐标系的X轴平行于裂纹面且垂直裂纹前缘，Y轴垂直于裂纹面.沿裂纹面的路径以裂纹尖端为第1点，另外4个附加点取距离尖端最近的节点，每个裂纹面各2个，如图5所示.

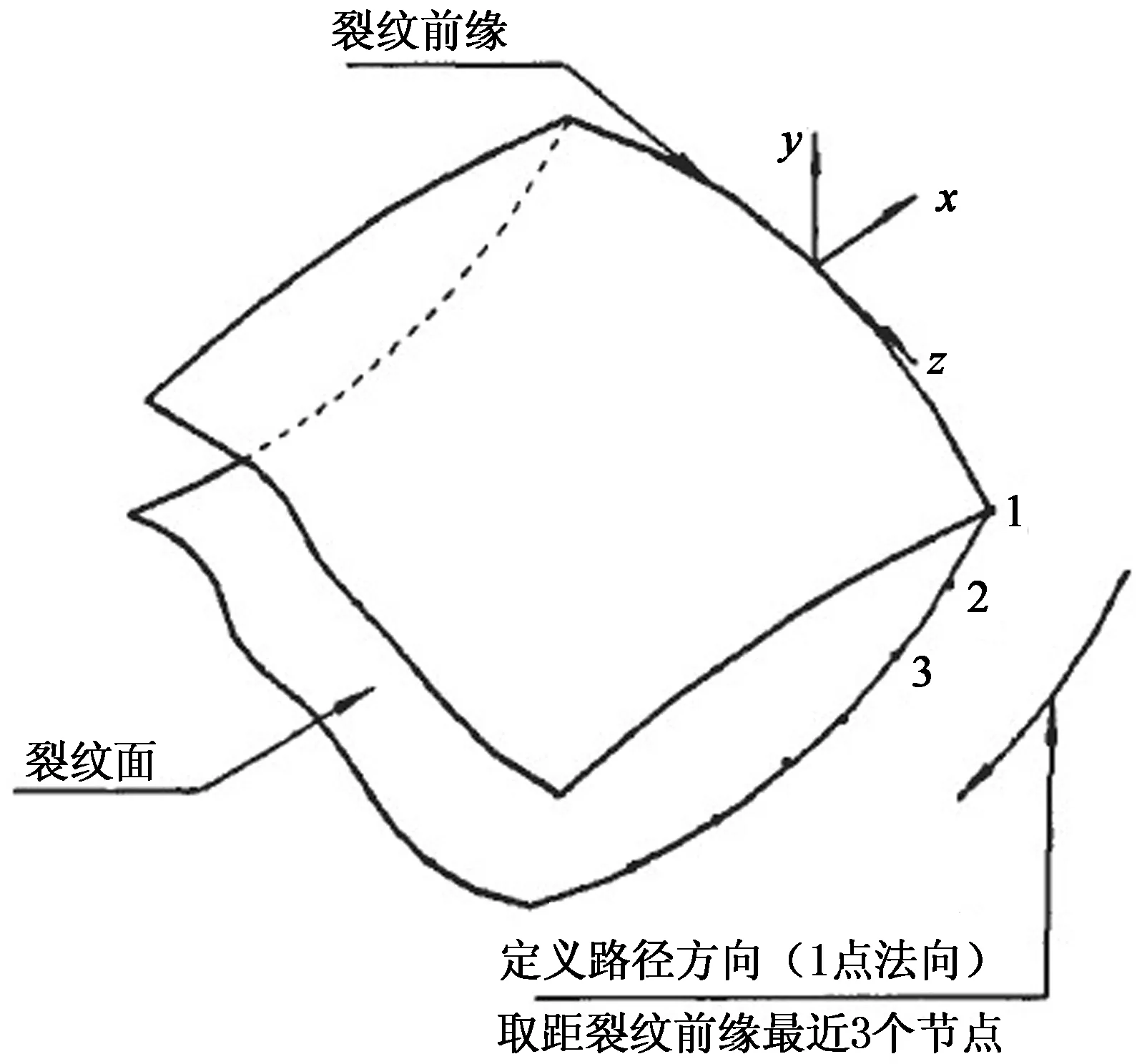
图5 裂纹前缘局部坐标系及路径定义

3 计算结果及分析

由于支柱瓷绝缘子受弯曲力作用，弯曲正应力方向与裂纹面垂直，故I型裂纹应力强度因子占主导地位，因而本文主要分析I型裂纹尖端应力场强度因子的变化规律，即裂纹形状比(a/b)、裂纹深度a、裂纹所处支柱位置及加载载荷变化对应力强度因子的影响.计算结果表明，裂纹前缘不同位置处的K值有所不同，分布呈现规律性，选取裂纹前缘各点中的两个表面点和一个最深点作为重点来考察应力强度因子在裂纹前沿的分布情况.

3.1 裂纹位置对 KI 的影响

形状、尺寸相同但在构件中位置不同的裂纹，其尖端应力强度因子不同.为此，本文设计的单条半椭圆表面裂纹分别位于瓷绝缘子支柱表面的上、中、下3处(y=855 mm，509 mm，107 mm)，其中上、下两处分别靠近上、下法兰口，裂纹形状比a/b= 0.5，裂纹深度a=1 mm，载荷Fx=16 kN，其他条件相同，分别计算三种情况下裂纹表面点及最深点的KI值，结果如图6所示.图中横坐标轴“0”表示裂纹最深点，“1”和“-1”表示裂纹两个表面点.

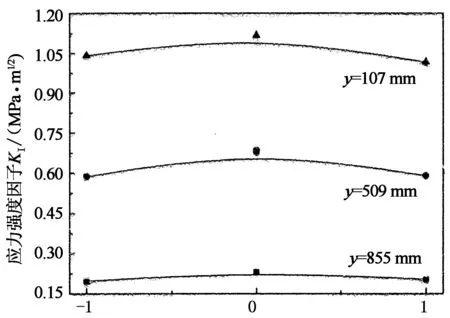
裂纹前缘相对位置

由图6可知，三种情况下裂纹前缘的KI值均为表面点最小，最深点最大.各点KI值关于最深点呈对称分布，且表面点与最深点KI差值随着裂纹向下移动而呈增大趋势.支柱表面相同形状和尺寸的裂纹从绝缘子顶部到底端，应力强度因子逐渐增大.其中下法兰口附近裂纹KI值最大达到1.117 MPa·m1/2，当载荷增大后，支柱下端的裂纹应力强度因子最先达到断裂韧性值，这与统计数据中支柱瓷绝缘子断裂部位95%以上位于法兰口内3 cm到第一瓷裙之间[12-14]相吻合.亦即支柱绝缘子的最小临界裂纹应位于支柱下端法兰口附近，因而此区域也应成为支柱瓷绝缘子无损探伤的重点区域.分析认为，弯曲受力情况下，支柱瓷绝缘子最底端伞裙根部与下法兰口之间为受力最大处(如图7)，裂纹如果位于这些区域或附近，更容易造成支柱绝缘子的破坏.

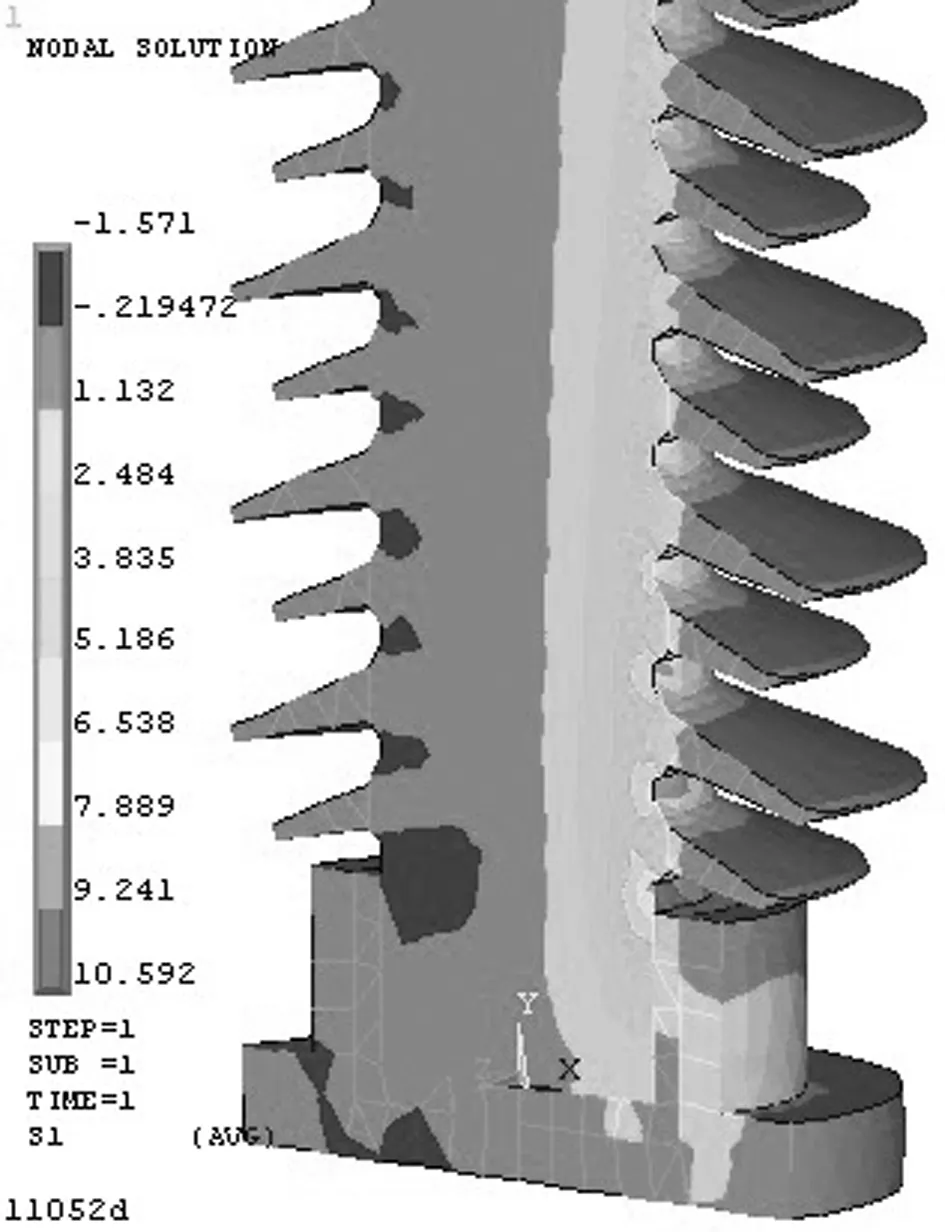
图7 绝缘子无缺陷时第一主应力S1分布(Fx=6KN)

鉴于上述分析，下文分析中主要对支柱绝缘子下法兰口附近(y=107 mm)的裂纹进行系统研究.

3.2 裂纹形状比(a/b)对KI 的影响

裂纹深度a保持1 mm不变，载荷16 kN，此时KI随a/b的变化规律如图8所示.

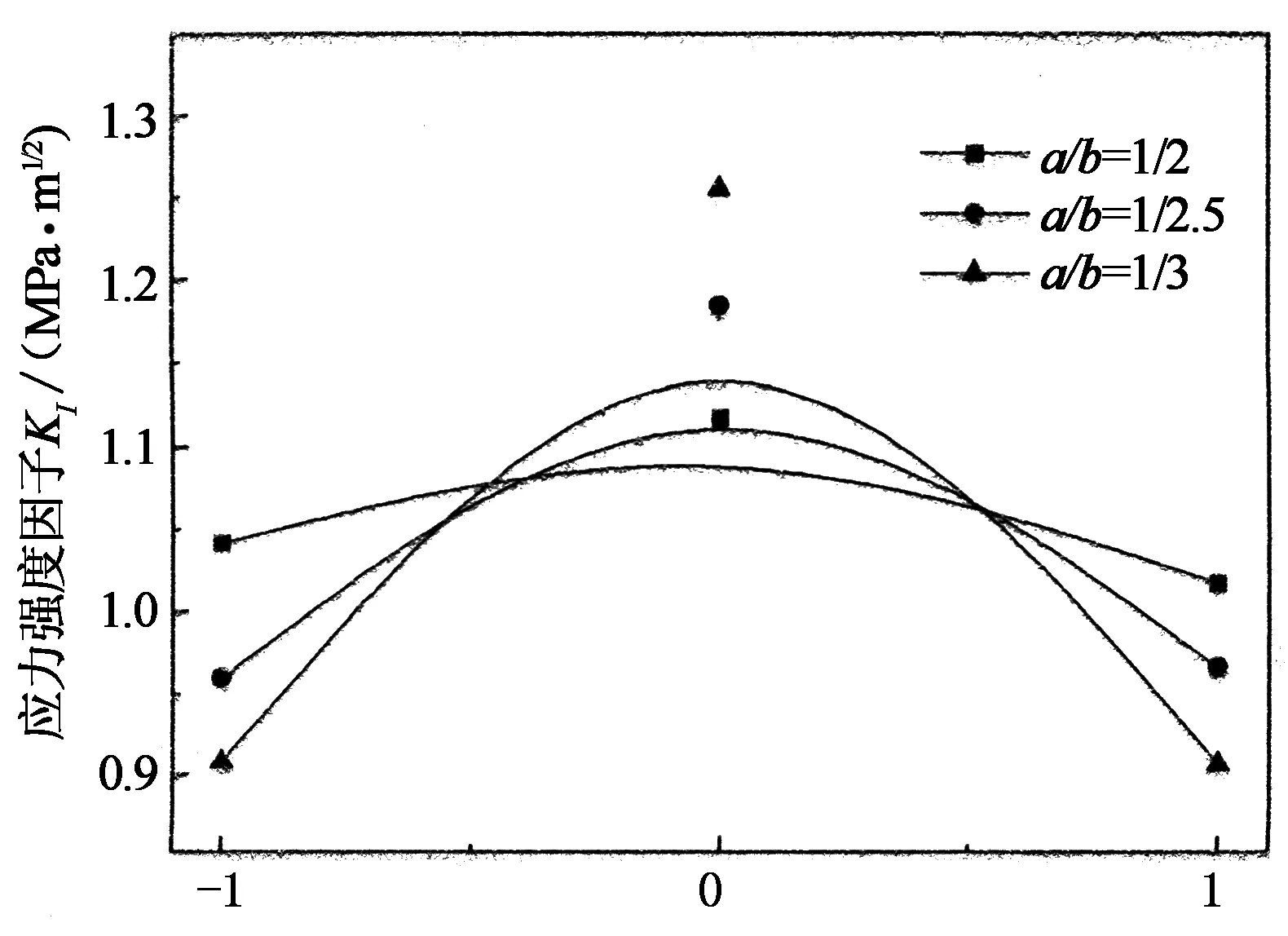
裂纹前缘相对位置

由图8不难看出，裂纹前沿椭圆率(a/b)较小的情况下，裂纹前缘中心点(最深处)有最大的KI值，表面点KI值最小.随着裂纹前沿趋向平直，中心点的应力强度因子逐渐增大，当a/b=1/3时，KI值达到1.255 MPa·m1/2，瓷件更容易破坏，而表面两点KI值逐渐减小，故中心点与表面点的差值也逐渐增大.

3.3 裂纹深度对KI的影响

当a/b= 0.5，Fx=16 kN，KI随裂纹深度的变化规律如图9所示.

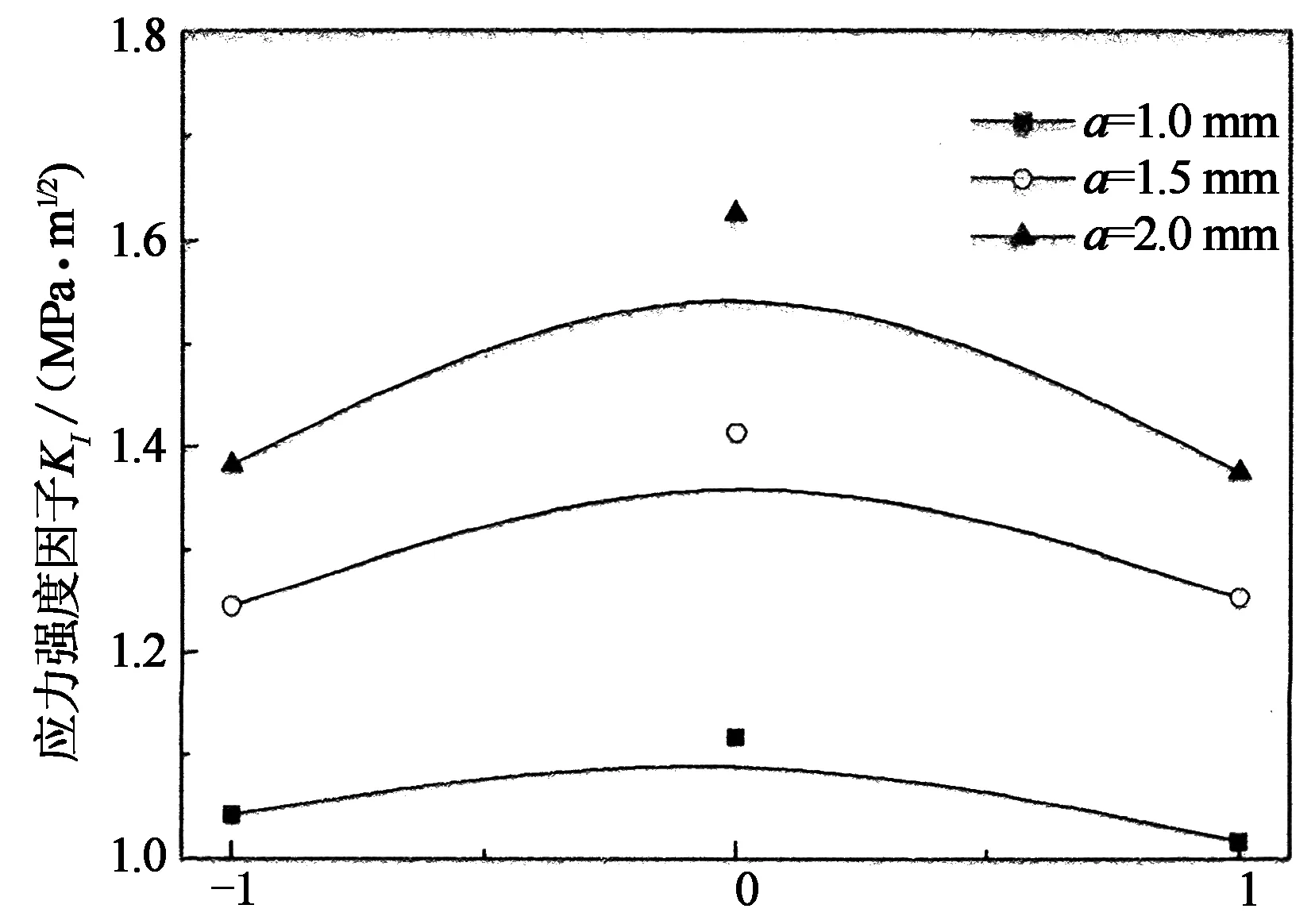
裂纹前缘相对位置

由图9可知，其它参数保持不变时，随着裂纹深度的增大，裂纹前缘各点的KI也逐渐增大，且表面点与最深点差值有增大趋势.当a=1.5mm时，KI=1.413 MPa·m1/2，a增大到2 mm时，KI增加到1.625 MPa·m1/2，当a继续增大则随着KI逐渐逼近KI(设为2 MPa·m1/2)，预计绝缘子支柱将产生破坏性后果.

3.4 加载载荷对KI的影响

当a=1 mm，b=2 mm时，KI随载荷变化情况如图10所示.结果表明，裂纹前沿各点应力强度因子随载荷变化呈线性关系，随着载荷的增加而增大，且最深点KI随载荷的增大趋势要略高于表面两点.由脆性材料的断裂力学理论可知，当载荷增加到一定程度，KI达到材料的断裂韧性时，裂纹失稳扩张，断裂迅速发生.反之，在额定载荷下，裂纹位置、形状一定时，通过有限元计算反推出临界裂纹尺寸，可为支柱瓷绝缘子无损检测所需灵敏度提供参考依据.

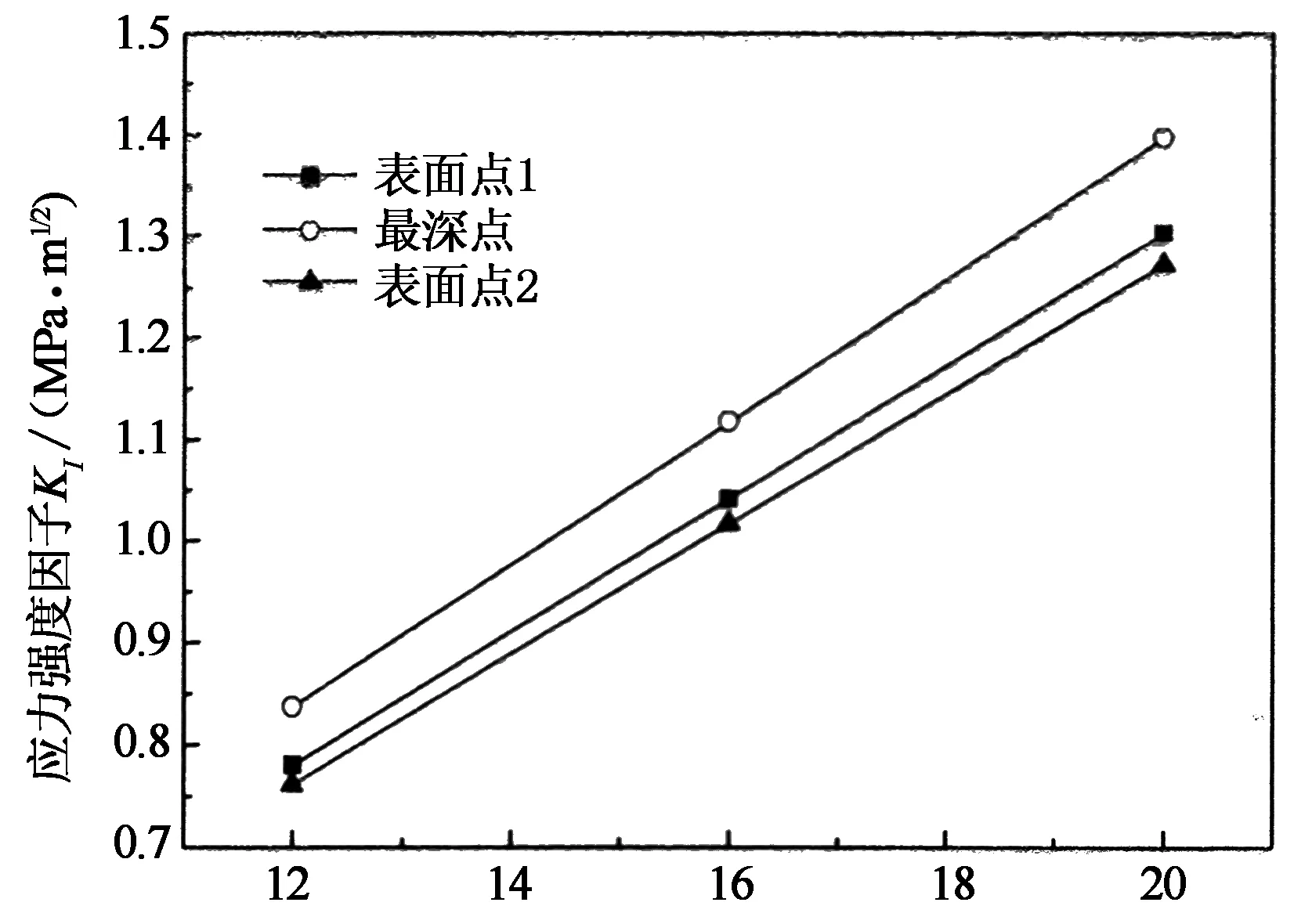
载荷x/kN

4 结 论

本文以支柱瓷绝缘子的弯曲破坏试验为原型，计算了多种情况下支柱表面半椭圆裂纹前沿各点的应力强度因子KI，得出主要结论如下：

1) 利用实体建模方法，通过在表面半椭圆裂纹前缘设置生成三维奇异单元，建立了含裂纹支柱瓷绝缘子弯曲破坏的有限元模型；

2) 采用1/4节点法计算不同尺寸、形状的裂纹尖端应力强度因子，结果表明裂纹前沿椭圆形状比较小的情况下，最深处具有最大应力强度因子，裂纹前缘各点的KI呈对称分布，且KI随裂纹深度的增大而增大，随椭圆率的增大而减小；

3) 支柱瓷绝缘子不同位置处的表面裂纹(形状、尺寸参数相同)对支柱应力分布的影响不同，尤其是靠近底端法兰口的表面裂纹缺陷，进一步加剧了缺陷附近的应力集中效应.通过对该处最小临界裂纹尺寸的分析，可确定绝缘子缺陷无损检测所需的灵敏度.

[1]瞿伟廉, 鲁丽君, 李明. 工程结构三维疲劳裂纹最大应力强度因子计算[J]. 地震工程与工程振动, 2007, 27(6): 58-63.

QU Wei-lian, LU Li-jun, LI Ming. Calculation of the maximum stress intensity factor of 3-D fatigue crack in engineering structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(6): 58-63. (In Chinese)

[2]马艳. 结构表面裂纹应力强度因子计算方法研究[D]. 大连：大连理工大学, 2007.

MA Yan. Study on method for calculating SIF of structural surface crack[D]. Dalian: Dalian University of Technology, 2007. (In Chinese)

[3]王永伟, 林哲. 表面裂纹的三维模拟及应力强度因子计算[J]. 中国海洋平台, 2006, 21(3): 23-26.

WANG Yong-wei, LIN Zhe. 3-D Simulation and stress intensity factors calculation of surface crack[J]. China Offshore Platform, 2006, 21(3): 23-26. (In Chinese)

[4]瞿伟廉, 鲁丽君, 李明. 带三维穿透裂纹结构的有限元实体建模方法[J]. 武汉理工大学学报, 2008, 30(1): 87-90.

QU Wei-lian, LU Li-jun, LI Ming. Solid modeling method for structure with 3-D straight through crack[J]. Journal of Wuhan University of Technology, 2008, 30(1): 87-90. (In Chinese)

[5]LIN X B, SMITH R A. Stress intensity factors for corner cracks emanating from fastener holes under tension[J]. Engineering Fracture Mechanics, 1999, 62(6): 535-553.

[6]IRWIN G R. Crack-extension force for a part-through crack in a plate[J]. Journal of Applied Mechanics, 1962, 29: 651-654.

[7]KASSIR M K, SIH G C. Three-dimensional stress distribution around an elliptical crack under arbitrary loadings(Three-dimensional stresses near border of discontinuity plane under arbitrary loading, obtaining solution for uniform shear applied to surface of crack)[J]. ASME, Transactions, Series E-Journal of Applied Mechanics, 1966, 33: 601-611.

[8]SMITH F W, KOBAYASHI A S, EMERY A F. Stress intensity factors for penny-shaped cracks: part 1—infinite solid[J]. Journal of Applied Mechanics, 1967, 34: 947-952.

[9]陈晓明, 矫桂琼, 崔振源. 复合型断裂准则在半椭圆表面裂纹问题中的应用[J]. 西北工业大学学报, 1986, 4(4): 385-393.

CHEN Xiao-ming, XU Gui-qiong, CUI Zhen-yuan, Application of combined-mode fracture criteria to semi-elliptical surface crack problems[J]. Journal of Northwestern Polytechnical University, 1986, 4(4): 385-393. (In Chinese)

[10]FEHL B D, TRUMAN K Z. An evaluation of fracture mechanics quarter-point displacement techniques used for computing stress intensity factors[J]. Engineering Structures, 1999, 21(5): 406-415.

[11]张朝晖.ANSYS12.0结构分析工程应用实例解析[M].3版.北京:机械工业出版社,2010.

ZHANG Chao-hui. ANSYS12.0 structural analysis instances for engineering application[M]. The 3rd edition. Beijing: China Machine Press, 2010. (In Chinese)

[12]王云昌. 支柱瓷绝缘子的超声波检测[J]. 江西电力, 2007, 31(3): 1-2.

WANG Yun-chang. The ultrasonic inspection for porcelain strut insulators[J]. Jiangxi Electric Power, 2007, 31(3): 1-2. (In Chinese)

[13]王维东, 刘勇. 支柱绝缘子及瓷套超声波探伤工艺方法研究[J]. 无损检测, 2006, 28(9): 460-462.

WANG Wei-dong, LIU Yong. Research on ultrasonic inspection technique of pillar insulators and porcelain cover[J]. Nondestructive Testing, 2006, 28(9): 460-462. (In Chinese)

[14]印华, 王谦, 王勇,等. 支柱瓷绝缘子断裂原因分析及检测方法[J]. 电力安全技术, 2007, 9(12): 47-48.

YIN Hua, WANG Qian, WANG Yong,etal. The failure analysis and detection methods for porcelain strut insulators[J]. Electric Safety Technology, 2007, 9(12): 47-48. (In Chinese)