基于元胞自动机带有隔离干预的传染病模型

刚家泰，戴钦武，李淑娟，谭欣欣*

（大连大学 信息工程学院，辽宁 大连 116622）

0 引言

传染病的爆发和流行一直都是困扰人们的重大问题。近年来发生的SARS、禽流感、甲型H1N1流感、艾滋病（HIV/AIDS）等，以及刚刚发生的H7N9型禽流感，给国民经济和人民生活带来了巨大的伤害。因此，对传染病预防和控制措施的研究已迫在眉睫。

元胞自动机模型具有时间上、空间上和状态上都离散的特性[1]，以局部规则同步演化来反映整个系统的复杂变化，这与传染病的传播机制十分相似，已经成为研究传染病学的一个重要方法。

文献[2,3]指出，传染病传播期间，缩短病人从发病到医院就医的时间，是疫情防疫中最先考虑的关键措施；文献[4]建立了元胞自动机模型,从医疗干预角度，研究了隔离治疗对传染病传播的影响；文献[5,6]利用元胞自动机模型对 SARS的传播进行了仿真模拟，提出较高的隔离水平对抑制传染病传播是十分有效的；文献[7]扩展了元胞自动机模型，建立了Agent动态网络的疾病传播模型，结合个体异质性研究了隔离力度对传染病传播的影响；文献[8]根据实际情况提出了一个与时间有关的带有隔离机制的病毒传播模型。

影响传染病传播的基本因素有个体的异质性，移动性以及发现疫情后政府采取的隔离措施，但同时考虑这三个因素对传染病传播的影响还少有研究。本文建立含有个体异质性、移动性和带有隔离干预措施的传染病数学模型，结合甲型H1N1流感染病人数的统计数据，对传染病的传播进行模拟仿真，进一步分析染病停留时间和隔离力度对传染病传播的影响，揭示传染病传播的防治机理。

1 SIQR传染病模型

根据传染病传播的特点，采用传染病动力学的建模思想，将研究人群划分为五类：易感者(S)，染病者(I)，隔离者(Q)，康复者(R)和死亡者(D)。其中S 是不具有免疫力的健康人群；I是已染病但未被隔离的人群，对外具有传染性；Q是染病后被隔离的人群，对外无传染性；R是经治疗痊愈的康复人群且具有免疫力；D为死亡人群，已退出传染病传播过程。整个传染病传播的流程图如图1所示。其中p为易感者被感染的概率，q为染病者被隔离的概率，µ为隔离者的恢复率，λ1，λ2为在染病期和隔离期人群的因病死亡率：

图1中，易感者本身没有传染能力，在自由环境下可以随机移动；染病者具有较强传染能力，当其移动到易感者邻域内或者易感者向它移动时，易感者将会以不同的概率被感染成为染病者；染病者会以一定的概率被隔离，隔离者失去了与外界接触交流的机会，不再具有传染能力；染病者无论是否被隔离，最终结果是治愈成为康复者或者因病死亡；康复者具有较长时期的免疫力，短期内不会再次被感染。

1.1 隔离干预

隔离干预是指对传染病传播过程中被感染的患者进行隔离治疗，使其避免与周围邻居接触交流，防止交叉感染和传染病的扩散。F.B.[9]提出：如果没有药物或者疫苗防治，对传染病传播的最重要和最有效的防控措施就是隔离干预；在防治传染病爆发或者流行期间，增加隔离的力度是最具成本效益的战略。Franks G. Ball[10]建立了关于传染病传播的SEIR随机模型，结果表明：有效的隔离干预对传染病传播的遏制效果显著性比单纯地对群体进行疫苗接种效果高。因此，研究对传染病传播的有效隔离干预，可以为控制传染病传播提供有力的理论支持。

假设传染病的传染方式是人与人的近距离接触和交流，一旦对染病者进行隔离干预，就可以达到控制疾病传播的目的。本文选取染病停留时间T和隔离力度q这两个参数，综合考察隔离干预这一机制对传染病传播的影响。

染病停留时间T，表示易感者通过与外界带菌个体接触后，从被感染上疾病到被隔离治疗这段时间间隔。T值越小，说明染病者被隔离的越早。

隔离力度q，表示染病者被隔离的概率，反映采取隔离措施的强度。q值越大，说明易感者和带菌个体相互间交流机会就越少，被传染的概率也就越小。

1.2 异质性

现实生活中，个体之间是有很大的差异性的[5,11]，易感者对疾病具有不同的抵抗能力Ri.j，染病者具有不同的传染能力fi,j，并且不同传染性的染病者具有不同的传染范围，即个体间存在异质性。为在模型中体现个体的异质性这一特点，引入有效接触传染概率

传染性疾病的传播与接触者之间的距离有关，接触者之间的距离越远，彼此被传染的概率越低，为进一步说明接触传染概率，本文引入距离影响因子[4]

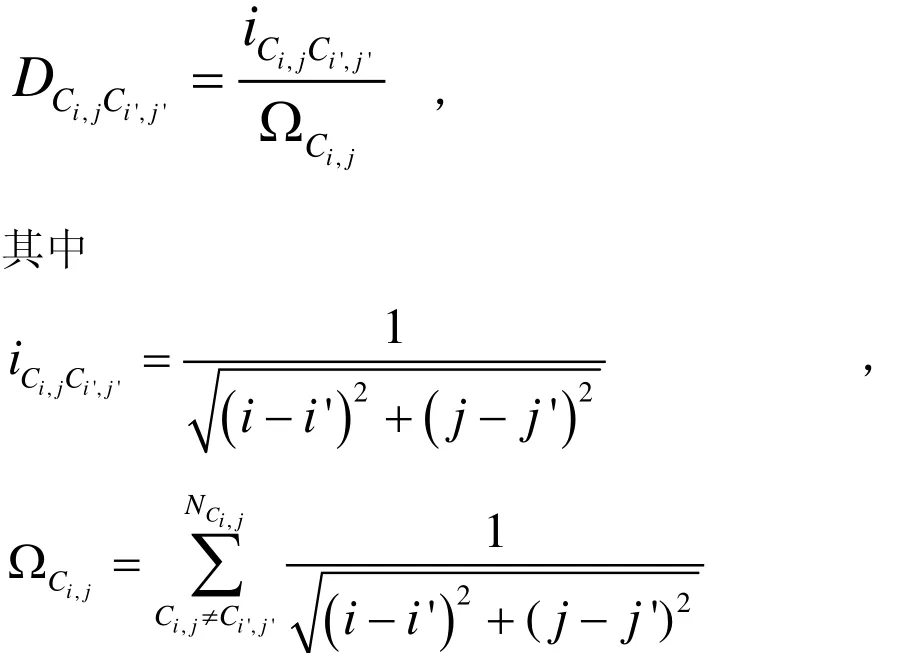
Ci,j为中心元胞，为其摩尔邻域内的任一邻居，是中心元胞Ci,j摩尔邻域内所有邻居集合。

综合这些因素，定义中心元胞Ci,j的有效接触传染概率Pi,j为：

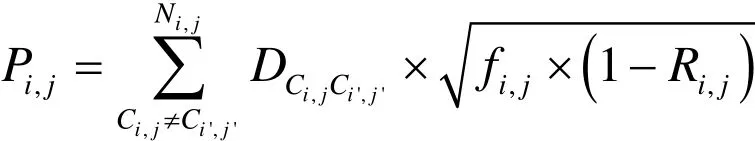
Pi,j值越大说明越容易被传染得病。

1.3 移动性

正是个体具有移动性，使得传染病得以传播。移动的比例足够大或者移动距离较远，会导致当地的传染病由无病状态转为地方性的流行状态，或者单一性的流行，严重时会导致当地政体的消失[12]。

个体的移动性反映了实际中个体的活跃程度，个体活跃程度越高，传染病的传播速度越快，越容易造成大规模的疫情爆发。

2 带有隔离干预的元胞自动机原理

元胞自动机是一个时间、空间和状态都离散的，通过局部元胞的相互作用而引起全局变化的动力系统模型[1,5]。可以用以下形式表达：

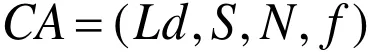
其中，CA 是指一个元胞自动机系统，Ld 表示d维的元胞空间，本文取d=2，L×L表示元胞空间网格的规模；S 表示所有元胞状态的有限离散集合；N 表示以某一元胞为中心的所有邻居状态的集合；f表示元胞状态局部转换函数。在每一离散的时间步，其转换规则为f:St+1=f(St,Nt)，即某一元胞下一时刻的状态由它当前时刻的状态和周围邻居的状态共同决定。

2.1 扩展的Moore邻域

本文将传统的 Moore邻域形式做一扩展，不仅考虑邻域内人群局部范围的交流，如家人，舍友、邻居等，同时还考虑个体随机与 Moore邻域外区域的人群交流，如工作需要的出差，远方朋友拜访等原因可能偶尔会接触到的邻居，这样更符合实际个体运动的特征。扩展的Moore邻域如图2所示。

在此基础上，借鉴随机行走元胞自动机的思想来描述个体的移动性，在每一时刻，都有一定比例(Percentage)的个体，以一定步长(Step)在网格空间中随机移动，即对网格中所有的元胞进行随机扫描，对扫面到的元胞，标记其坐标为(i , j)，同时生成两个独立的随机数di和dj(∣di∣≤Step,∣dj∣≤Step)，然后将(i , j)处的元胞与( i+di, j+ dj)处的元胞进行交换[13,14]，视为该元胞完成一次移动。

2.2 元胞状态演化规则

本文建立二维的L×L网格空间，将t时刻网格空间的元胞状态数值化，分别以{0,1,2,3,4}代表元胞Ci,j在t时刻{S,I,Q,R,D}五种状态。

设定所有元胞的初始状态=0，即所有的元胞都视为易感者，随机在该网格空间中取比例为0.0018的元胞作为初始染病者人数，设定其状态=1，称为网格空间中的传染病源。自t=0时刻开始，在每一个离散的时间步对网格空间的所有元胞进行扫描，并按以下规则进行元胞状态更新。

当=1时，元胞Ci,j为染病者，设T1为染病周期，当t＜T1时，患者仍然处于染病期，在传染病传播过程中将以概率q被隔离，此时=2；当t＞T1时，染病者将被强制隔离，为=2。设病死率为λ1，染病期间部分染病者因病死亡，状态变为死亡者，即=4；

当=2时，元胞C为隔离者，代表隔离者， i, j设T2为隔离周期，在该周期内，被隔离的染病者经过治疗，以一定的概率µ痊愈成为康复者，即更新状态为=3，康复者在免疫周期T3内保持很高的免疫力。隔离治疗期间会有部分染病者死亡，设病死率为λ2，状态转为死亡者，即=4。

当=3时，元胞C为康复者，代表康复者，i, j在免疫周期T3内具有较高免疫力，不会再次被感染；

在每一个仿真步，对所有的元胞都先进行一次随机扫描，对扫描到的元胞给予记录，然后按照所定义的最大步长和移动比例进行随机行走或者移动。

基于以上的演化规则，网格空间中所有元胞在每一仿真步将同步更新，局部元胞之间的相互作用结果，就是下一仿真步整个群体的状态。

3 模型的仿真与结果分析

3.1 模型的仿真

根据SIQR模型的传染病传播流程，将以上元胞状态演化规则应用于扩展的摩尔邻域，对传染病传播过程进行仿真模拟。设定网格空间由L×L=100×100的单元格构成；初始感染概率为0.0018；每一步演化过程都会有Percentage=0.1比例的元胞，以最大的移动步长Step=10进行移动。本文选取2009年6月16日至7月15日期间发生于中国境内的甲型H1N1流感数据进行仿真模拟，根据中华人民共和国卫生部数据[15]统计，假设易感者感染流感病毒后病发时间为7天，病死率为4%。由于甲型H1N1流感没有相关的复发情况报道，认为康复者的免疫周期为365天。图3显示 40天内的模拟仿真数据, 结果与实际数据较为吻合。

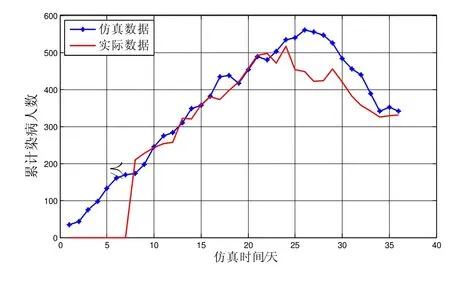
图3 甲型H1N1实际数据和模拟仿真数据对比

由图3可以看出，甲型流感在传播初期，没有受到任何的干预影响，流感病毒传播速度较快，染病累计人数很快达到高峰，随后开始缓慢下降。染病人数下降的原因，一是染病人数死亡，退出了传播周期，导致被感染的人数减少；二是流感病毒传播后期受到控制，染病个体被隔离进行治疗痊愈后成为康复者，使得群体中被感染的人数减少。

为进一步说明流感病毒传播期间，隔离干预对传染病传播的影响，在设定的参数条件下，对上述仿真模型中的染病停留时间T和隔离力度q分别进行变量调控，具体地分析隔离干预对传染病传播的影响。

3.2 结果分析

3.2.1 染病停留时间T对传染病传播的影响

保持初始参数数值不变，通过改变仿真过程中的染病停留时间T的数值，研究染病停留时间的长短对传染病传播过程的影响。图4表示分别取不同的染病停留时间T=5天、T=9天时累计染病人数和实际情况的累计染病人数对比。

从图4可以看出，在病人被感染后，提前两天将其隔离，即染病停留时间为T=5天时，累计染病人数增加速度将会大大地减缓，染病人数达到峰值远低于实际数据下的峰值；而如果推后两天隔离，染病停留时间为T=9天时，累计染病人数增加速度则会迅速加大，短时间就可以达到较高的数值，不仅高于实际情况，而且处于高峰期的时间也较长。

病人所处的染病停留时间越长，病人在自由环境下活动的时间越久，接触的易感者就越多，最终病人累计的人数就越多。所以，当传染病疫情爆发初期，及时减少病人处于自由环境下的滞留时间，缩短病人自被感染到隔离治疗的染病停留时间，能够对传染病疫情起到明显的抑制作用。因此，减少病人的染病停留时间是控制传染病传播的一个关键因素。

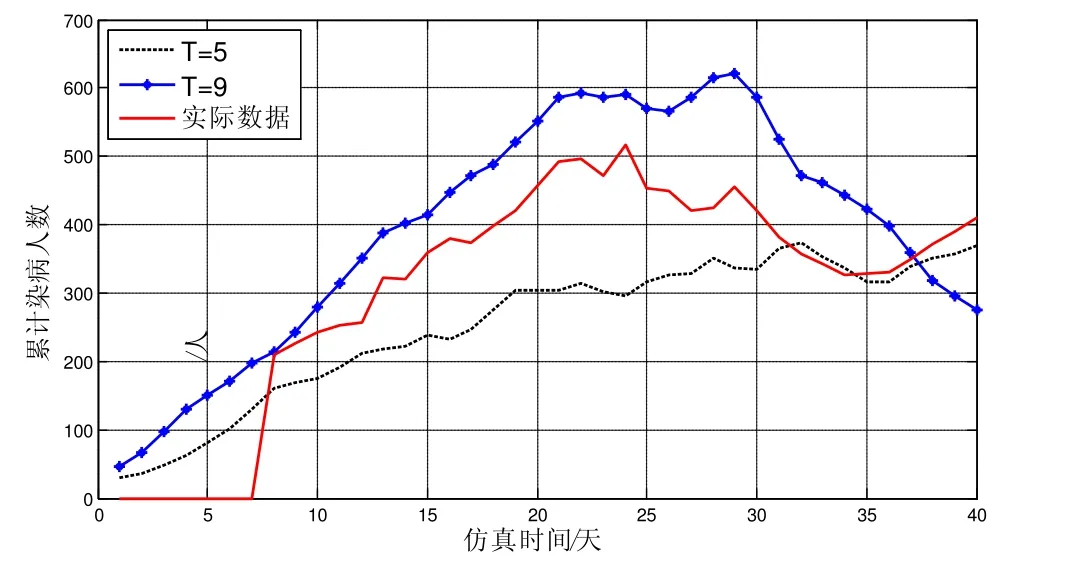
图4 不同的染病停留时间对甲型流感H1N1传播的影响

3.2.2 隔离力度q对传染病传播的影响

隔离干预的实施，不仅与染病停留时间有关，同时也和对染病者采取的隔离力度有关。对上述模型进行修正，保持染病停留时间不变，改变隔离力度大小，分析隔离力度对传染病传播的影响，分别取q=0.15、q=0.35和q=0.55，图5显示了不同隔离力度对传染病传播的影响。

图5 不同隔离力度对甲型流感H1N1传播的影响

从图5可以看出，在传染病传播过程中，隔离力度越大，累计染病人数越少，控制传染病疫情的效果越显著。当q=0.15时，部分染病者由于被隔离治疗，减少了他们与外界的接触交流机会，被感染的人数减少，累计染病人数增加趋势较为缓慢；当q=0.35时，进一步增大对染病者的隔离力度，累计染病人数相对实际情况有了大幅度的下降；当q=0.55时，传播初期，累计染病人数增加的趋势较缓慢，短时间达到峰值后逐渐减少，疫情得以控制。因此，隔离力度对传染病传播具有重要影响，隔离力度越大，传染病传播越容易得到控制，当隔离力度足够大时候，传染病来不及传播就得以控制。

4 总结

本文建立了基于元胞自动机的SIQR模型，并以甲型H1N1流感为例进行了模拟仿真。该模型说明了人们对已知或未知的传染病传播采取积极严格的隔离干预是十分必要和有效的。仿真结果表明：传染病传播初期，由于人们及相关部门对其不了解或者防范意识不深，未及时采取相应的防控措施，短时期内造成疾病的迅速扩散，发展为大范围内的疫情爆发；及早采取隔离措施，加大对染病者的隔离力度，减少患者的染病停留时间，可避免染病者在自由环境下滞留时间过长而产生更广范围的传染。染病停留时间越短，隔离力度越大，被感染的病人就越少，传染病传播持续的时间越短，对传染病传播疫情的控制效果越显著。

同时，本文不仅考虑家人，舍友、邻居等近距离人群之间交流的局部范围，还考虑工作需要的出差、远方朋友拜访等原因可能偶尔会接触到的个体间交流，使个体的移动性更贴近实际。因此, 在元胞自动机原有的邻域的基础上，提出了扩展的Moore邻域,并对传染病的传播过程进行模拟仿真。

随着研究的深入，将进一步改进完善模型，并结合中华人民共和国卫生部网提供的真实数据，考虑接种疫苗、初始感染率和传染病病毒变异频数等因素，从微观角度分析探究传染病的传播机理，预测传染病疫情的发展趋势，为政府部门制定传染病的防控措施提供最有力的理论支持。

[1]Bastien Chopard, Michel Droz. 物理系统的元胞自动机模拟[M]. 祝玉学, 赵学龙, 译. 北京: 清华大学出版社, 2003:10-12.

[2]Donnelly C A, Ghani A C, Leung G M, et al. Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong [J]. The Lancet, 2003,361(9371): 1761-1766.

[3]Riley S, et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions[J]. Science, 2003, 300(5627): 1961-1966.

[4]Chao Guan, Wenyan Yuan, Yun Peng. A Cellular Automaton Model with Extended Neighborhood for Epidemic Propagation[C]. Fourth International Joint Conference on Computational Sciences and Optimization, 2011.

[5]于鑫, 段晓东, 刘向东, 等. 基于元胞自动机的传染病传播模型及模拟[J]. 计算机工程与应用. 2005(2): 205-209.

[6]高宝俊, 张廷, 宣慧玉, 等. 基于异质元胞自动机的SARS传播[J]. 系统工程理论方法应用, 2006, 15(3): 205-209.

[7]李玮, 毕贵红, 等. 基于 Agent动态网络的疾病传播模型[J]. 计算机工程, 2012, 38(1): 24-28.

[8]姚丽丽, 马英红, 李慧嘉. 一种带隔离机制的 SIS模型研究[J]. 计算机安全, 2010(2): 91-92.

[9]F B Agusto. Optimal isolation control strategies and cost-effectiveness analysis of a two-strain avian influenza model [J]. Bio Systems, 2013(113): 155-164.

[10]Frank G Ball, Edward S, Knock Philip D, et al. Control of emerging infectious diseases using responsive imperfect vaccination and isolation[J]. Mathematical Biosciences, 2008,216: 100-113.

[11]G Ch Sirakoulis, I Karafyllidis, A Thanailakis. A cellular automaton for the effects of populaton movement and vaccination on epidemic propagation [J]. Ecological Modeling, 2000, 133: 209-233.

[12]Guiquan Sun, Quanxing Liu, Zhen Jin, et al. Influence of infection rate and migration on extinction of disease in spatial epidemics [J]. Journal of Theoretical Biology, 2010, 264:95-103.

[13]Martinsa M L,Ceottoa Gl. A cellular automata model for citrus variegated chlorosis [J]. Physica A, 2001, 295: 42-48

[14]Jiatai Gang, Pengyan Shi, Sanshan Gang. A epidemic Model with Inhomogeneity And Mobility based on Cellular Automata [J]. Advanced Material Research, 2013, 709:871-874.

[15]中华人民共和国国家卫生和计划生育委员会. 卫生部甲型 H1N1流感防控工作信息通报[EB/OL]. http://www.nhfpc.gov.cn/search/search.jsp.