基于有限元方法的运动磁体电磁场的计算

韩长军

（辽东学院 信息技术学院，辽宁 丹东118003）

有限元方法(FEM, Finite Element Method)于本世纪60年代被提出，广泛应用于磁场仿真计算。由于经典电磁场理论过于复杂，人们通过研究提出许多新的方法，其中最常用的是有限元方法，该方法是把求解域看作有许多小的在节点处连接的子域构成，其模型给出基本方程的近似解。有限元软件是基于有限元计算方法，运用计算机软件的形式把有限元方法表现出来，这样既减少了计算时间，也节省了人力。对电磁场进行分析的有限元软件很多，比较有影响力的有：美国Swanson Analysis System的ANSYS有限元产品；美国MacNeal Schwendlert Corp.MSC/EMS软件；加拿大Integrated Engineering Software Inc.的系列产品以及美国 Ansoft corp.的 Maxwell软件等，其中以ANSYS的使用者最多。ANSYS的分析领域很广泛，主要包括力学分析、热与温度场分析、耦合场分析、电磁场分析等[1]。

在麦克斯韦方程组提出以后，电磁场理论已经相当完美，人们根据这一方程组把电磁场理论的应用可谓发挥到及至。麦克斯韦方程组完整而充分地反映电磁场的客观运动规律，使其成为求解电磁场问题的基本依据[2]。当导体垂直切割匀强磁场的磁感线时，其两端会产生电动势；当磁体穿过闭合线圈时，线圈中会产生电流，并且电流所产生的磁场将阻碍磁铁的运动；旋转磁极式发电机发电，也是根据切割原理在线圈中产生电动势；还有现在的流体发电，也是利用流体在流过磁场过程中会切割磁感线产生电动势[3-5]。所有这些都是由于导体与磁体发生了相对运动，从而在导体中激发出电动势。那么假如在这些情况下撤去导体，即磁体相对周围空间发生相对运动，则在它的周围电磁场又是如何？从理论上来说，运动的磁铁必然引起周围磁场的变化，这样也就会激发出电场[6-7]，但这种电磁场如何分布、是否会像通常的时变场一样形成电磁波动，即是否以电磁波的形式向远处传播，这正是本文所研究的课题。

本文在麦克斯韦方程组的基础上，推导出应用于运动磁体电磁场的理论模型，并利用有限元ANSYS软件，对磁体电磁场进行仿真计算，并对结果进行了详尽的分析。

1 理论

1.1 麦克斯韦方程组

麦克斯韦方程组是麦克斯韦对安培环路定律、法拉第电磁感应定律、磁通量连续定律和高斯通量定理的总结、修正和推广，这一定律使得电磁理论得到了完善，并成为时变电磁场理论的基础[8]。

麦克斯韦方程组微分形式为[9]：

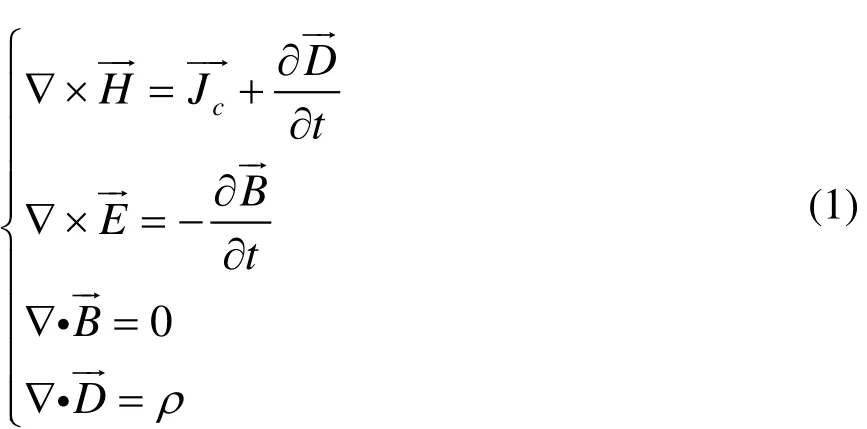
由式(1)可以看出时变电场是有散有旋的，因此电力线可以是闭合的，也可以是不闭合的，闭合的电力线和磁力线相互铰链，不闭合的电力线从正电荷出发，终止于负电荷；而时变磁场是散有旋的，因此磁力线必须是闭合的，闭合的磁力线与电流相铰链。

由式(2)可以看出，在这种情况下，时变电场和时变磁场都是有旋无散的，电力线和磁力线是相互铰链、自行闭合的，即变化的电场会激发出变化的磁场，变化的磁场也会激发出变化的电场，因此在时变场中，这种不断的相互激发，使得它们互相转化，并在自由空间中将这种转化向远处传播，形成电磁波动。

1.2 运动磁体理论模型推导

假使磁铁为圆柱形，使运动磁铁周围的电磁场用静止的磁铁周围的电磁场表示，设一坐标系为 K坐标系，并设另一坐标系 K'系，它相对磁铁静止，即该系以速度v向+Z方向运动，为分析方便，以下使用柱形坐标进行计算。

将式(3)和式(4)代入麦克斯韦方程组式(2)，可以得到：

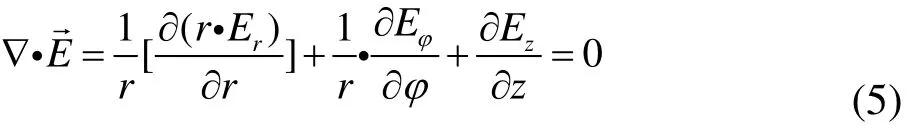
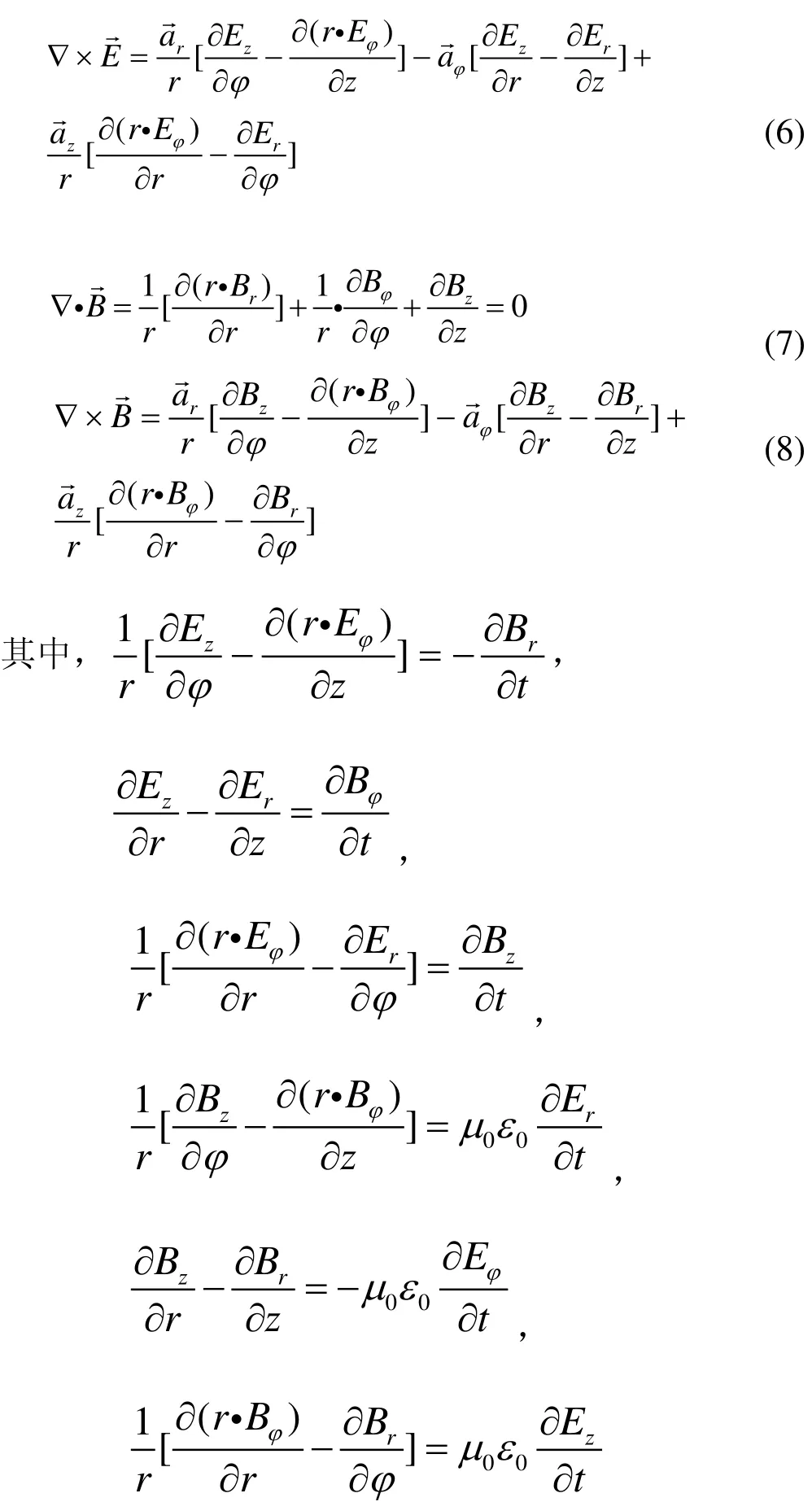
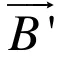
同样将式(9)和式(10)代入麦克斯韦方程组中，得出类似于K系中在K’系中的式子，即

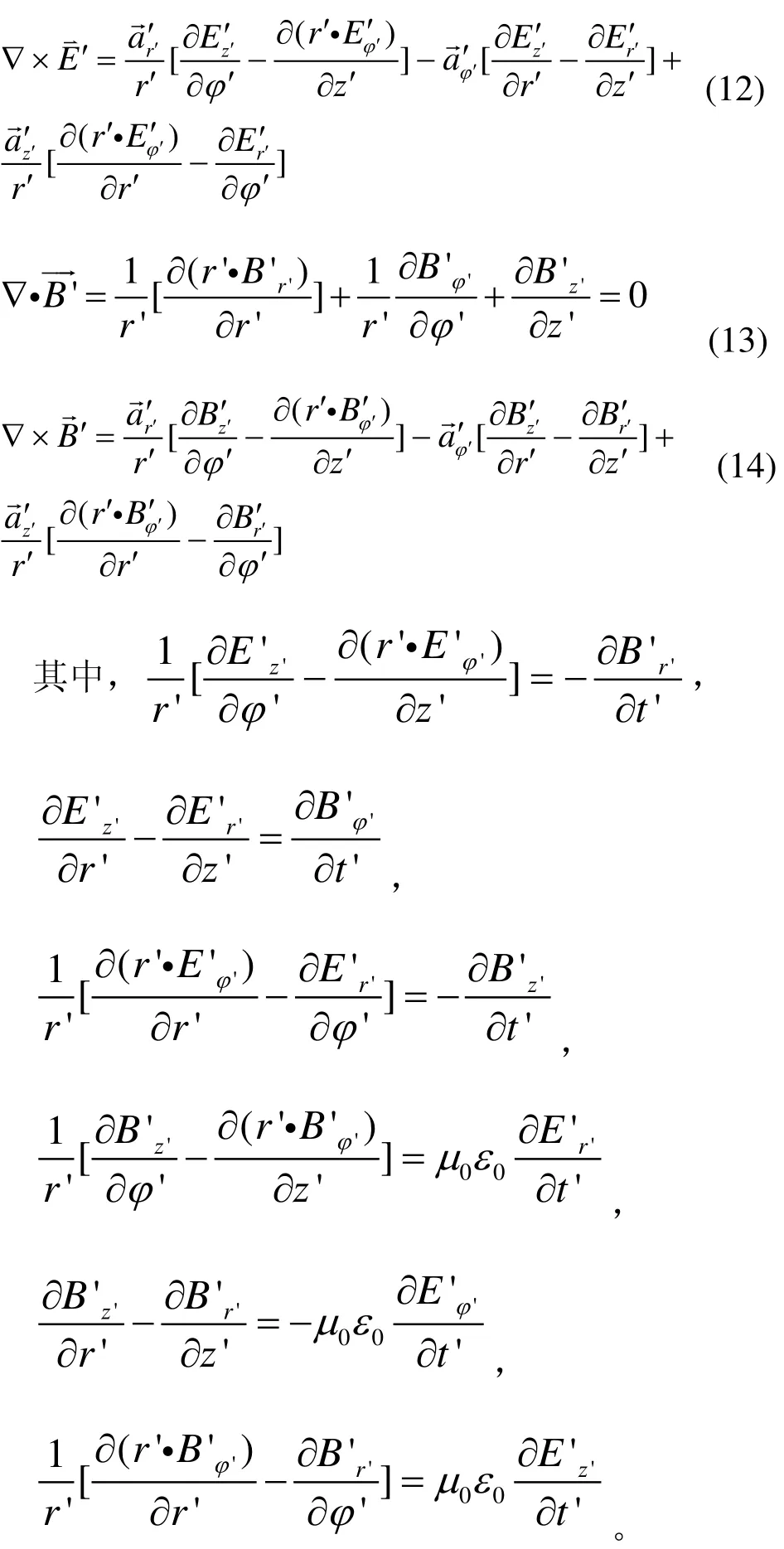
把 k系中的时间和空间变量用 k’系中的时间和空间变量表示。根据洛伦兹变换：

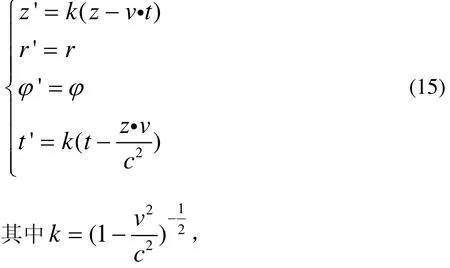
对式(15)分别对 r，ϕ，z，t求偏导数，将原 K系中各式与 K’系中的对应方程各个对应项相等，经整理归纳，最终可以得到：

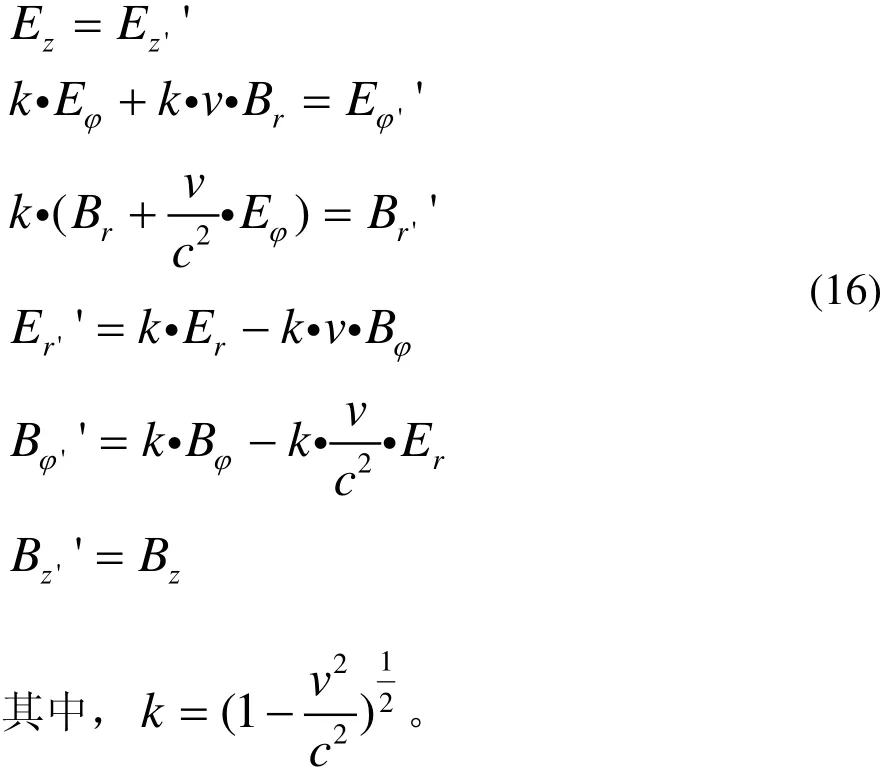
将式(16)中的v用-v代替，可以得到相应的反向变换关系式。

由于磁铁相对K’系静止，所以磁铁在K’系中的电磁场分布即为静态磁铁的电磁场分布，静态磁铁周围磁场分布是固定的，并不发生变化，所以其周围并不会产生电场，因此运动磁铁在 K’系中电场为零，即：E'= 0，E'= 0，E '= 0。在k’系中，在r'ϕ'z'方向上的值为零，即Bϕ''= 0。将这些条件代入式(16)，可以得到运动的磁铁的周围的电磁场的分布，即

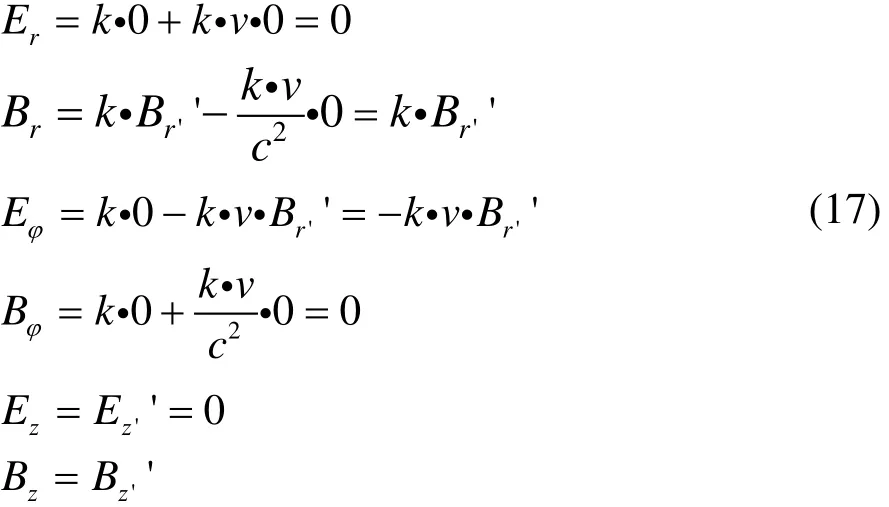
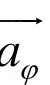
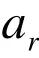
由推导我们还可知磁铁周围的电磁场分布，并不是以相互激发的形式存在，某一点的磁场仅仅随相对磁铁的位置的变化而发生变化，在该点激发出电场，这种变化并不是其周围电磁场变化的原因，因为其周围电磁场的变化也是仅仅随它们各自相对磁铁的位置的变化而发生变化，所以匀速运动的磁铁不会产生电磁波向外辐射。

2 仿真实验与结果分析

2.1 实验模型建立

由于磁铁具有严格的对称性，所以可以用二维进行仿真，并且只在第一象限即可。设空气的相对磁导率为1，磁体的相对磁导率为非线性，为10000设；设置空气和磁铁的单元类型，然后创建模型形状，如图1(a)所示；进行网格划分，如图1(b)所示。然后进行界面限制和加载，最后对磁场进行计算和后处理[12]。

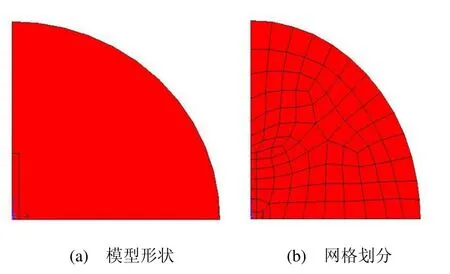
图1 磁体模型

2.2 实验结果与分析

任取两横向节点间的磁通密度，曲线图如图4(a)所示，图4(b)为两节点之间的连线间各节点在x方向上的磁通密度变化曲线，图4(c)为两节点之间的连线间各节点在y方向上的磁通密度变化曲线。

从图4中可以看出，所取的路径两点的为横向路径，且磁通密度为越来越偏离磁体，则无论x方向还是y方向的磁通密度值都越来越小，最后接近于零。对于x方向来说，开始值会有小的增加，但随后则呈现递减趋势，且正负方向有所改变。这是由磁力线的疏密程度所决定的。

建立另一条竖直路线，如图5所示。从图5中可以看出，x方向的磁通密度呈现递减趋势，而对于y方向的磁通密度来说，首先逐渐增长，增长到一定程度呈现递减趋势，且递减的程度没有横向路径大，这是因为，所取的竖直路径的两点，随之y方向坐标值的增加，越来越靠近磁感应线密集区域，所以y方向磁通密度越来越大，当路径超过磁力线范围时，没有磁力线，或者相当少，则y方向的磁通值减少，接近于零。

根据式(18)磁感应强度和电场强度的关系式，在图3(a)和图4(a)两条线上的电场强度的大小变化曲线分别与图3(b)和图4(b)变化趋势一样。

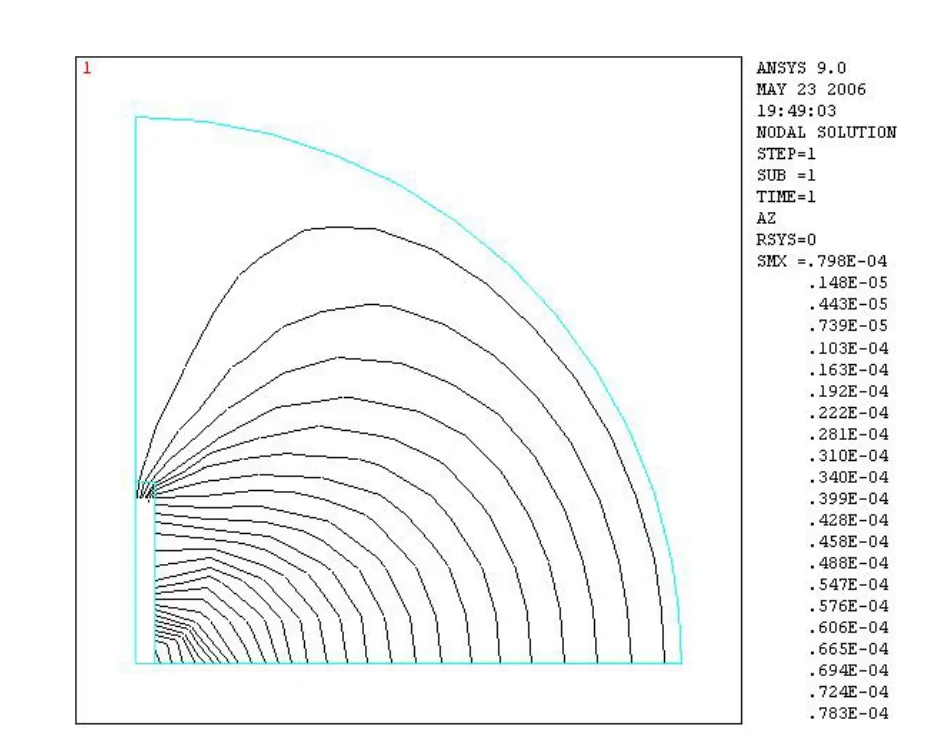
图2 磁力线分布

图3 各节点和单元的磁通密度分布

图4 任意横向两点磁通密度图

图5 任意竖直两点磁通密度图

3 结论

通过对运动磁体周围磁场的推导计算，可以得到其理论模型，这有助于引导人们更好的熟知运动磁体磁场分布，便于更深入的研究。而本文借助于有限元方法对磁体周围磁场进行仿真，这样不仅可以验证所推导理论模型的正确性，可以用一种新型的有限元方法对磁体周围磁场进行计算，对于今后还可以继续进行更细致的推导验证和更复杂的计算[13-14]。

通过推导和仿真，可以对知识更深入延伸，若在磁铁的正上方或正下方放一线圈，就会产生顺时针或逆时针方向环形电流。因为正是磁铁激发了一定形式的电场，在这种电场的驱动下，线圈中的自由电子就会沿顺时针或逆时针方向运动，所以会产生环形电流。匀速运动的磁铁虽然可以激发电场，但并不会产生电磁波向外辐射。因为电磁波的产生，是由于变化的电场周围激发变化的磁场，这种激发的磁场又会在其周围激发变化的电场，正是这种相互激发方式使能量向远处传播，因为这种能量是以电磁场的形式传播的。

[1]商跃进. 有限元原理与ANSYS应用指南[M]. 北京: 清华人民出版社, 2005: 172.

[2]唐建群, 刘启华. 电磁学与电信技术发展简述[J]. 南京工业大学学报, 2006(2): 145.

[3]贾起民, 郑永令, 陈暨耀. 电磁学: 第二版[M]. 北京: 高等教育出版社, 2001: 265.

[4]徐游. 电磁学: 第二版[M]. 北京: 高等教育出版社, 2004:78.

[5]冯恩信. 电磁场与波[M]. 西安: 西安交通大学出版社,2000: 2-5.

[6]程守洙, 江之水. 普通物理学 1: 第五版[M]. 北京: 高等教育出版社, 1997: 189.

[7]程守洙, 江之水. 普通物理学 2: 第五版[M]. 北京: 高等教育出版社, 1997: 159.

[8]马冰然. 电磁场与微波技术: 第二版[M]. 广州: 华南理工大学出版社, 2000: 312.

[9]施偌谷. 麦克斯韦与电磁场理论的建立[J]. 漳州师范学院学报, 2000(3): 116.

[10]QIU Yao feng, CAO Yi, LI Zheng fan. Solving electromagnetism differential equations based on random walk [J].Journal of Shanghai Jiaotong University, 2004(3): 136.

[11]CHAN C T, LI Jensen, FUNG K H. On extending the concept of double negativity to acoustic waves [J]. Journal of Shanghai Jiaotong University: Science, 2004(3): 50-54.

[12]雷银照. 关于电磁场数值分析的若干认识[J]. 电工技术学报, 1997(6): 168.

[13]张乐乐, 谭南林, 焦风川. ANSYS辅助分析应用基础教程[M]. 清华大学出版社北京交通大学出版社, 2006: 213.

[14]唐兴伦, 范群波, 张朝晖, 等. ANSYS工程应用教程——热与电磁学篇[M]. 中国铁道出版社, 2003: 236.