地面干扰源定位问题中飞机参数估计新方法

李 丽

（大连大学 信息工程学院，辽宁 大连 116622）

0 引言

在无线电频率管理及民航系统中，民用航空频段时常收到地面的恶意无线电信号干扰，严重威胁飞机安全。目前，我国无线电台的数目日益增加，导致民航收到干扰的机率也日益增大。因此，为了保障民航飞机安全飞行，恶意的无线电信号干扰定位就变得越来越重要。

由于飞机的飞行高度比较高，导致通信信号的覆盖范围比较广，可达到数十万平方公里。那么在这个范围内的信号干扰源都会对飞机的安全飞行造成一定的威胁。然而，目前在无线电频率监测方面主要采用地面监测，该检测手段的缺点是监测的范围比较有限，有时会存在接收不到干扰源信号的问题。如果采用空中监测，会受到空中管制以及经济费用等原因的制约，从而无法实现干扰源的查找和定位。而且对于恶意干扰以及人为对抗因素等的影响，使得空中监测无法实现。在已知飞机状态信息的前提下，可以根据回波信号中的多普勒频率实现对干扰源的定位。文献[1]根据回波信号中的多普勒频率中包含干扰源的位置信息，来构建非线性方程，通过对方程组求解，实现了对干扰源的定位。文献[2]提出了采用高斯近似粒子滤波方法进行定位地面干扰源。这些文献都能够实现干扰源的定位，但是他们都有一个前提，那就是飞机的运动状态信息是已知的。若不能获得飞机的实时的状态信息，则地面干扰源的定位不能实现。因此飞机的运动状态信息的精确估计是非常重要的。本文主要研究飞机运动状态的精确估计，为后续干扰源的定位奠定基础。

1 新的信号模型

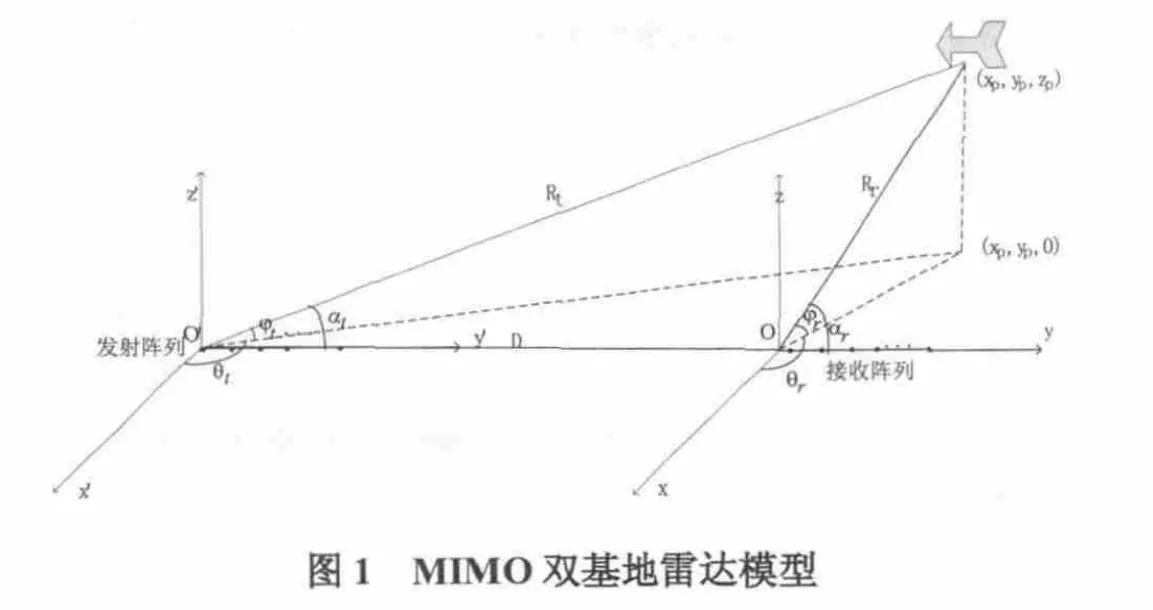
对地面干扰源的定位我们可以使用双基地MIMO雷达系统的原理来实现。双基地MIMO雷达的阵列模型如图1所示。假设发射阵列和接收阵列均采用均匀线阵，且阵元数目分别为M和N。阵元间距均为λ2（λ为波长）。发射阵和接收阵基线距离为D；飞机相对发射阵列的方位角和俯仰角分别为θt和ϕt，而θr和ϕr为相对于接收阵的方位角和俯仰角。

设第m个发射阵元发射的信号为

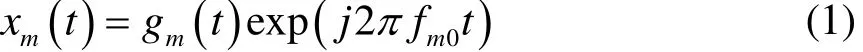
其中fm0为发射信号频率，gm(t)为幅值。回波信号是具有多普勒频率的多径分量的叠加信号。因此，此时远场的回波信号模型已经不再适用。本文提出一个改进的近场双基地 MIMO雷达阵列信号模型，第 n个接收阵元接收的回波信号为

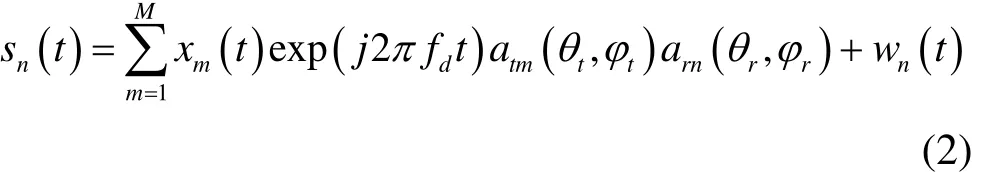
其中，fd和µ分别为多普勒频率的初始频率和调频率，atm(θt, ϕt) = exp ( −jπ(m−1) sinθtc osϕt)为发射导向矢量。

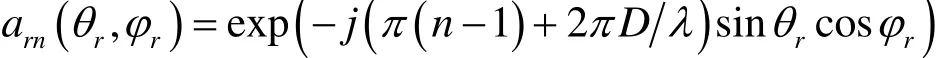
为接收导向矢量。wn(t)为均值为0方差为1的高斯白噪声。

相干MIMO雷达的特点是各发射阵元发射的信

其中xq(t )和xk(t)分别表示第q个和第k个发射阵元的发射信号，*为共轭运算。利用该相互正交特性，可以实现对回波信号进行匹配滤波，从而得到匹配滤波后的信号为

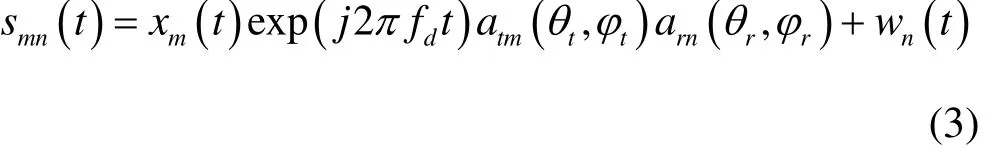
N个接收阵元接收到的散射信号经匹配滤波后的输出可以写成下面的形式

2 目标跟踪及运动状态估计

首先对smn(t)进行频谱分析，在频域内通过谱峰搜索得到频率的粗略估计值；再在频率粗略估计值的左右范围内进行M点CZT细化，以获取更高精度的频率估计值；最后，采用类 Rife算法进行进一步的修正，得到最终载频估计值[4]。

接下来，本文构造两个子阵R1和R2为

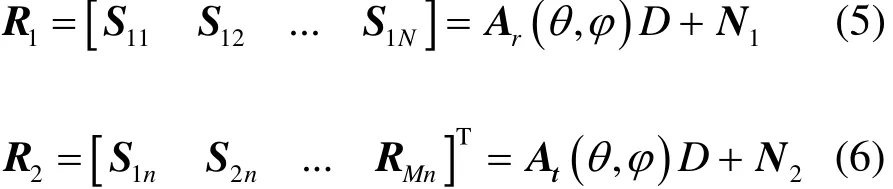
构造子阵R1的相关矩阵RR1R1

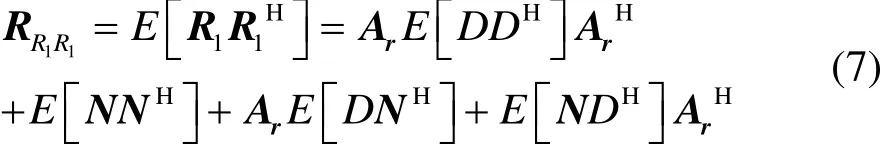
由于信号与噪声不相关且相互独立，对RR1R1进行特征分解有

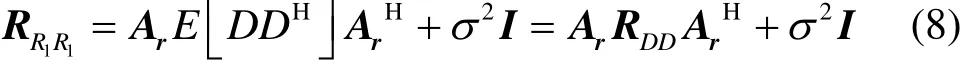
其中UD和UN分别对应着信号子空间和噪声子空间。

根据二维MUSIC算法[5-7]得到二维MUSIC空间谱为：

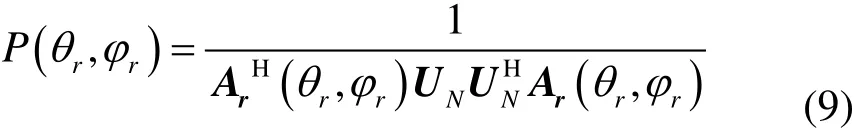
对P(θr, ϕr)进行峰值点搜索，可实现θr和ϕr的联合估计。

类似的，矩阵R2的二维MUSIC空间谱为

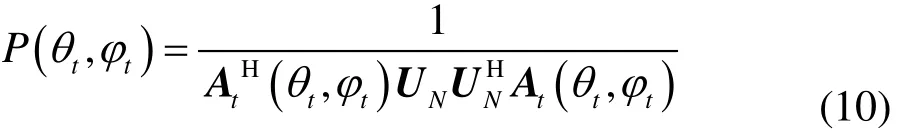
3 仿真实验

仿真实验中，发射阵元的数目M=6，接收阵元数目N=8，D=5Km。假设飞机相对于发射阵列和接收阵列的 2维方位角和俯仰角分别为(θt, ϕt, θr, ϕr)=(6 0,30,50,20)。飞机沿Y轴方向的速度分量为 200 m/s。产生的多普勒频率为fd=28.7939。采样频率为100M加入均值为0、方差为1的高斯白噪声。仿真实验中，Monte-Carlo实验的次数为500。

仿真实验一：在本次仿真实验中，研究了本文所提出的算法性能与快拍数之间的关系。假设信噪比SNR=15dB。图2和图3给出了目标相关参数随快拍数变化的曲线。图中快拍数从200按步长100变化到2000。

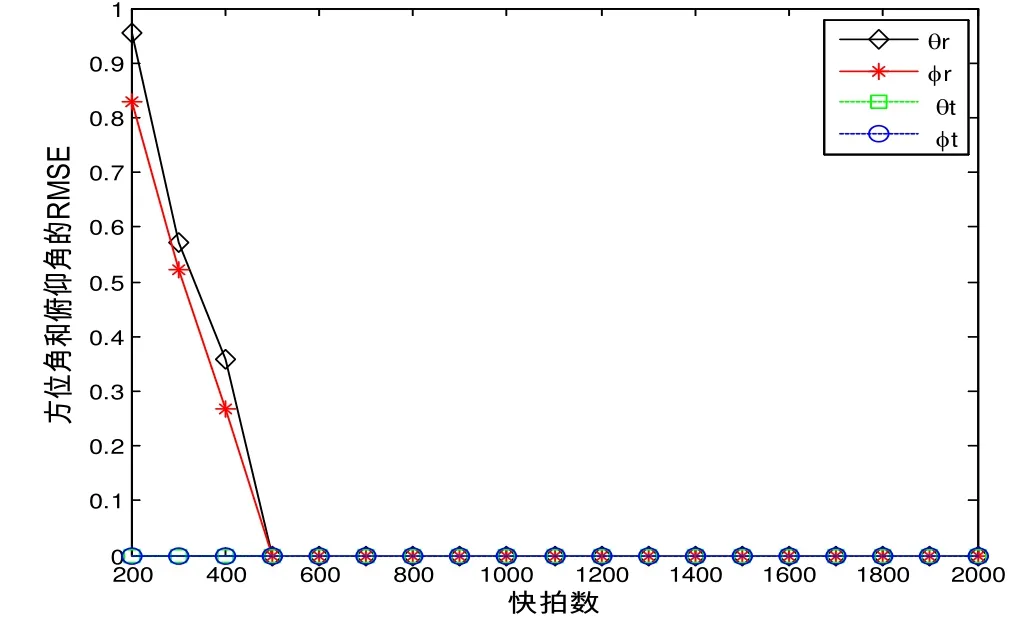
图2 方位角和俯仰角的RMSE随快拍数的变化曲线

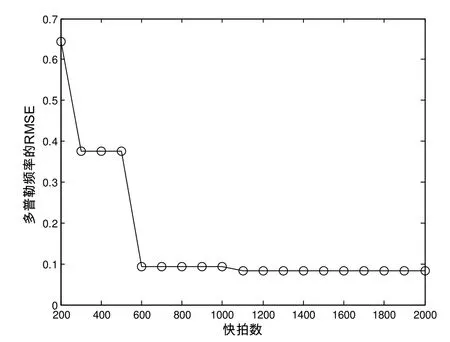
图3 多普勒频率的RMSE随快拍数的变化曲线

可以看出，随着快拍数的增大，目标参数估计的RMSE逐渐减小，当我们能够发现快拍数大于600时，参数估计的性能趋于稳定。因此下面的实验中，快拍数取为800。

仿真实验二：讨论本文算法性能与SNR的关系。在这个仿真实验中取快拍数为1000。图4和图5给出了目标对应参数随信噪比变化的曲线。图中信噪比从0dB按步长2dB变化到30dB。

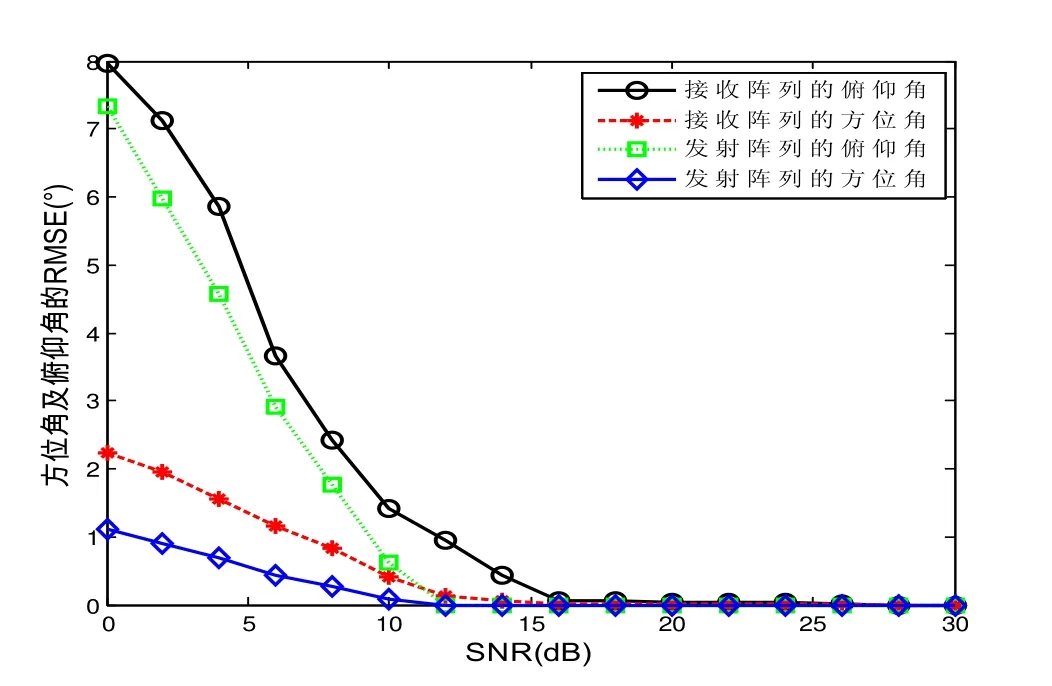
图4 方位角和俯仰角的RMSE随信噪比变化的曲线

图5 多普勒频率的RMSE随信噪比变化的曲线

从图4、图5可以看出，随着信噪比的提高，目标相应参数的 RMSE逐渐减小。可见本文算法能够实现飞机参数的较高精度估计。

4 结论

本文研究了地面干扰源定位问题中飞机运动参数的联合估计。由于飞机的运动状态信息对于实现定位地面干扰源的位置起到了很重要的作用。因此，本文首先提了一个新的信号模型，实现了了多普勒频率的估计，接下来对飞机的俯仰角和方位角采用二维MUSIC算法进行了较好估计。通过实验仿真验证了本文所提出算法的估计性能。

[1]谭海峰, 李景春. 利用飞机散射信号查找干扰源的定位算法[J]. 无线电通信技术, 2009, 35(2): 40-42．

[2]邱天爽, 夏楠, 李景春, 等. 稳定分布噪声下基于高斯近似粒子滤波的干扰源定位算法[J]. 信号处理, 2012, 9(28):1248-1253.

[3]张永顺, 郭艺夺, 赵国庆, 等. MIMO双基地雷达空间多目标定位方法[J]. 电子与信息学报, 2010, 32(12): 2820-2824.

[4]黄富彪, 何冰哲. 一种卫星信号载波频率精确估计算法[J].现代电子技术, 2012, 35(3): 129-134.

[5]Wu Shilong, Luo Jingqing, Liu Youjun. A method for recognition of spectrum peaks in 2-D MUSIC algorithm [C].IEEE International Symposium on Microwave, Antenna,Propagation and EMC technologies for Wireless communications, 2005, 1(1): 704-707.

[6]Jiangfeng Li, Xiaofei Zhang. Improved joint DOD and DOA estimation for MIMO array with velocity receive sensors [J].IEEE Signal Processing, 2011, 18(12): 717-720.

[7]张贤达. 现代信号处理[M]. 清华大学出版社, 2004,11.

[8]Tsao T, Slamani M, Varshney P, et al. Ambiguity function for a bistatic radar [J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 1041-1051.

[9]杨明磊, 陈伯孝, 齐飞林, 等. 多载频 MIMO 雷达的模糊函数[J]. 系统工程与电子技术, 2009, 31(1): 5-9.