基于θ-D方法带落角约束的三维末制导律设计

王洪雪, 李新国, 王晨曦

(西北工业大学 航天学院, 陕西 西安 710072)

0 引言

传统的制导律设计方法是在滚动为零的假设下,将飞行器的运动解耦为俯仰、转弯两个通道,然后在两个通道上分别设计制导律,从而将三维制导问题转化为两个二维制导问题[1]。但对于高超声速滑翔飞行器,由于采用BTT控制方式,滚动为零的假设不再成立,两个通道之间存在强烈的耦合关系,双通道解耦的制导律设计方法不再适用。

文献[1]利用李群方法获得了非解耦的三维制导律,该制导律能够满足终端速度方向要求,但制导律形式比较复杂,涉及许多矢量和矩阵计算,不易于工程实现。文献[2]结合微分几何和李群方法的优点,设计了一种带落角约束的新型三维制导律,但该制导律同样包含矢量和李群运算,在仿真平台和弹载计算机上实现有一定的难度。

最优控制理论在解决非线性系统问题时,直接求解哈密尔顿-贝尔曼-雅可比(HJB)方程十分困难。针对这种情况,文献[3]提出了θ-D非线性次优控制方法,该方法能够克服上述困难,可以获得HJB方程的近似闭环解,控制精度高,计算量小,已成功应用于导弹六自由度非线性自动驾驶仪设计[4]和导弹制导控制一体化设计[5]。

本文基于θ-D方法,建立了飞行器-目标三维运动方程,在不进行通道解耦的条件下,通过重新定义状态变量,设计了一种满足落角约束的三维制导律。该制导律制导精度高,计算量小,可实时生成制导指令,易于工程实现。

1 问题描述

飞行器与目标的相对运动关系及坐标系如图1所示。其中,Oxyz为惯性坐标系;Oxtytzt为视线坐标系;O,M分别为目标和飞行器;r为目标指向飞行器的视线矢量;ξ,ε分别为视线方位角和高低角。图中规定ξ,ε,η符号为正;θ,ψV,φ,δψV符号为负。

图1 相对运动关系及坐标系Fig.1 Relative motion and coordinate system

在视线坐标系中,视线坐标系相对惯性坐标系的旋转角速度为:

(1)

则:

(2)

由于d2r/dt2=a(a为飞行器的加速度矢量),则飞行器与目标的相对运动方程为:

(3)

式中,axt,ayt,azt为飞行器加速度矢量在视线坐标系中的投影。

飞行器的运动方程组为:

(4)

式中,γ为弹道倾角;ψV为弹道偏角;σ为倾侧角;D为气动阻力;L为气动升力。

2 θ-D次优控制方法

考虑如下非线性时变系统:

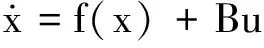
(5)

取性能指标函数为:

(6)

式中,x∈Rn;f∈Rn;B∈Rn×m;u∈Rm;B为常值矩阵;Q为n阶半正定对角矩阵;R为m阶正定对角矩阵;f(x)连续可微,且f(0)=0为平衡状态。该无约束非线性调节器的最优解可通过求解如下HJB偏微分方程得到:

(7)

式中,V(x)为性能指标函数的最优值,即:

(8)

V(x)连续可微,且V(x) ≥ 0。最优控制为:

u=-R-1BT∂V/∂x

(9)

由于该最优控制中包含有∂V/∂x项,需要求解HJB偏微分方程。然而,一般情况下求解HJB方程是非常困难的,这也限制了最优控制理论在非线性系统中的应用。

在式(6)中引入扰动项,则指标函数变为:

(10)

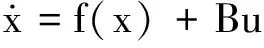
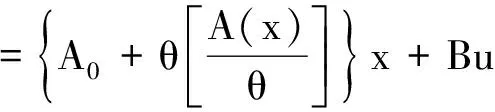
(11)

式中,A0为常数矩阵,且[A0,B]为稳定对象,[A0+A(x),B]逐点可控。令λ=∂V/∂x,结合式(10),可将原HJB方程(7)整理为:

(12)

假设λ可表示为θ的幂级数,即:

(13)

式中,Ti为待定矩阵。将式(13)代入式(12),并将θ的幂系数置为0,整理可得如下方程组:

(14)

(15)

…

(16)

其中:

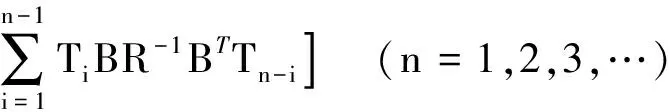
(17)

式中,ki,li>0为可调参数(i=1,2,3,…,n)。θ-D次优控制为:

u=-R-1BT∂V/∂x=-R-1BTλ

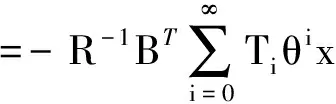
(18)

显然,式(14)为代数黎卡提方程,从中很容易求得T0;式(15)和式(16)为关于Ti的线性李雅普诺夫方程,很容易求解,具体步骤参见文献[5]。在求解式(18)的过程中,中间变量θ可由Ti与θi相乘消去。从控制量的求解过程中可以发现,θ-D次优控制方法可以获得非线性系统的闭环控制,且计算量不大,可应用于非线性系统的实时次优控制。

3 θ-D三维末制导律设计

结合式(5)、式(11),重新定义状态变量,并将相对运动方程(3)整理成如下形式:

(19)

其中:

A(X)=

式中,A0为常值矩阵,可任意选取,本文取为初始点处A(X)的值。

经简单分析即可发现,在飞行器接近目标的过程中视线高低角ε逐渐趋近于弹道倾角的绝对值|γ|,且在目标点附近,两者近似相等。因此,可将对落角的约束转换为对视线高低角的约束,即要求飞行器命中目标时,ε=-γf。这可以通过在θ-D控制算法中设置成目标值来实现,即:

(20)

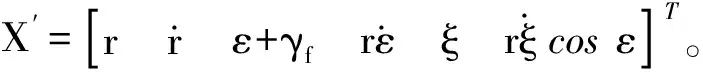
一般情况下,扰动项Tiθi只需计算前三项即可满足制导精度的要求,则θ-D三维末制导律为:

U= -R-1BT(T0+T1θ+T2θ2)×

(21)

4 制导指令生成

本文飞行器采用BTT-180控制方式,制导指令为迎角α和倾侧角σ。假设飞行器飞行过程中保持侧滑角为零,控制系统理想工作。

由于所设计的制导律计算出的加速度指令是在视线坐标系中,需要将该指令变换到弹道坐标系中。视线坐标系到弹道坐标系的变换矩阵为:

(22)

则加速度指令在弹道坐标系中为:

(23)

飞行器所受重力和气动力的合力在弹道坐标系中的投影为:

(24)

则:

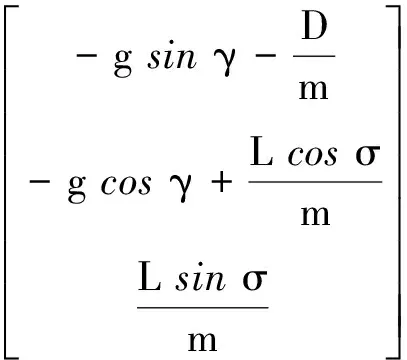
(25)

根据式(25)可得:

(26)

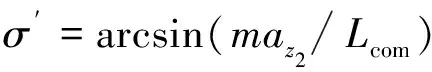
(27)

根据式(26),可得飞行器的升力系数CL=Lcom/(qSref),迎角指令αcom可根据CL在当前高度和马赫数下反插值求得。

由于飞行器倾侧角的范围为-180°～180°,需要对式(27)进行变换以得到倾侧角指令。令χ=ay2+gcosγ,有:

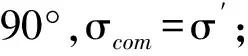
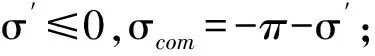
5 仿真结果及分析

本文以CAV-H为对象,迎角范围为0°～20°,落角约束γf=-90°。仿真初始条件:飞行器初始位置(60,30,-80)km,V0=1600 m/s,γ0=-10°,ψV0=-137°,α0=10°,σ0=0°,目标在坐标系原点,A0=A(X0)。状态权重矩阵Q和控制权重矩阵R的选取对制导律的性能有很大的影响,本文按如下原则选取:在初始时刻,飞行器与目标距离较远,视线角变化较慢,对制导精度要求不高,状态权重系数可以取小一些,以避免产生较大的控制量。当飞行器接近目标时,为了获得较高的制导精度,需要较大的权重系数。同时,由于对飞行器终端速度大小和视线方位角没有约束,相应的状态权重系数可以取得很小。相关参数选取如下:

Q=diag(2e4/r,1e-3,6.8e12/r,9.5e6/r,

1e-3,1.65e8/r)

R=diag(5e5,3e5,3e5)

l1=l2=10,k1=k2=0.9

仿真结果如图2～图5所示。图2和图3分别为飞行器的三维弹道曲线和弹道倾角变化曲线。可以看出,飞行器飞行弹道光滑平稳,经82.05 s命中目标,着地点为(0.54,-0.44) km,弹道倾角收敛到-89.2°,能够满足制导精度的要求和落角约束。图4和图5分别为迎角变化曲线和倾侧角变化曲线。从图中可以看出,在18.6 s前,飞行器以最大迎角飞行,主要是为了使飞行器航向快速对准目标;48.7 s后,飞行器迎角增大主要是为了下压弹道,使弹道倾角收敛到期望落角,最后迎角迅速减小,收敛至2.8°,末端迎角较小。

图2 三维弹道曲线Fig.2 3D trajectories

图3 弹道倾角变化曲线Fig.3 Flight path angle curve

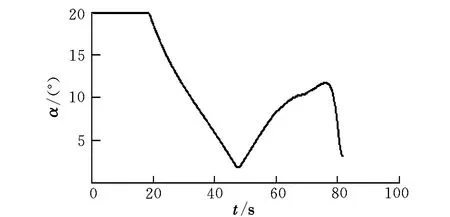
图4 迎角变化曲线Fig.4 Angle of attack curve

图5 倾侧角变化曲线Fig.5 Bank angle curve

6 结束语

本文基于θ-D次优控制方法,设计了一种满足落角约束的三维末制导律。对于采用BTT控制方式的飞行器,该制导律不需要进行通道解耦,是一种具有闭环形式的次优制导律,控制精度高,计算量小,易于工程实现。仿真结果表明,本文所设计的制导律能满足制导精度要求和落角约束。同时,本文对于存在强烈耦合作用的BTT飞行器的制导系统设计具有一定的参考意义。需要说明的是,该制导律并没有考虑目标的机动和随机干扰因素的影响,其打击机动目标的能力和鲁棒性有待进一步验证。

参考文献：

[1] 韩大鹏,孙未蒙,郑志强,等.一种基于李群方法的新型三维制导律设计[J].航空学报,2009, 30(3):468-475.

[2] 彭双春,潘亮,韩大鹏,等.一种新型三维制导律设计的非线性方法[J].航空学报,2010,31(10):2018-2025.

[3] Xin M,Balakrishnan S N.A new method for suboptimal control of a class of nonlinear systems[J].Optimal Control Applications & Methods,2006,26(2):55-83.

[4] Xin M,Balakrishnan S N,Stansbery D T,et al.Nonlinear missile autopilot design with theta-Dtechnique[J].Journal of Guidance,Control, and Dynamics,2004,27(3):406-417.

[5] Xin M,Balakrishnan S N,Ohlmeyer E J.Integrated guidance and control of missiles withθ-Dmethod[J].IEEE Transactions on Control Systems Technology,2006,14(6):981-992.