扩展卡尔曼滤波确定飞机失速速度的方法
徐 骏 驰
(民航上海航空器适航审定中心 飞行性能室, 上海 200335)
0 引言
失速速度作为飞机的基本性能数据是确定起飞速度、进近速度等关键参数的基础。目前,大部分飞机型号合格审定申请人所采用的方法是:用拖锥提供基准静压源来修正机载静压传感器的位置误差以获得校正空速。采用该方法可以在大部分速度范围内提供较精确的静压参数,但是在低速段由于出现气流分离,飞机可能会出现抖振、飞机高度不断降低等不稳定状态,导致由拖锥直接测得的数据不理想。为此,部分申请人采用了结合DGPS高度和静温对拖锥测得的气压高度进行修正,进而得到相对精确的失速速度。该方法对数据的精确性有一定提升,但需要在试验点前后保持一段时间的稳定飞行状态,而且不能存在逆温层。
本文提出了一种不依赖于拖锥数据,采用扩展卡尔曼滤波算法估算静压值从而得到失速速度的方法。该方法经过飞行试验验证,并与拖锥法的结果进行了对比。试验表明,在对试验数据进行滤波处理后,可以成功地获取较为精确的结果。
1 扩展卡尔曼滤波
卡尔曼滤波的状态估计算法能较为准确地对目标的运动位置和速度做出预测,但简单卡尔曼滤波器仅适用于线性的随机系统,不能直接应用到非线性问题中。通过在当前估计值附近将非线性函数进行一阶或二阶泰勒展开,舍弃高阶分量,从而将非线性模型简化为线性函数,就可以继续使用卡尔曼滤波器,这种方法即扩展卡尔曼滤波(Extended Kalman Filter,EKF)[1]。
可以将民用大型运输类飞机和测量系统视为非线性系统,由此可以通过非线性随机微分方程建立相应的飞机动态模型和测量系统模型。
(1)
式中,f∈Rn,h∈Rm为非线性函数;x∈Rn为状态矢量;u∈Rn为输入/控制矢量;y∈Rm为输出矢量;z∈Rm为离散点上的样本点,具有一致的采样频率;矢量w和v为随机的过程噪声及测量噪声。尽管认为过程噪声是随机变量,但通过对模型进行近似处理可以确定一些动态参数。认为该噪声的平均值为0,是高斯白噪声。假定这些噪声相互独立,受初始状态x(0)的影响,有:
(2)
式中,R为测量噪声;Q为系统随机噪声。
对方程组(1)求偏导数,得到雅克比矩阵如下:
(3)
可以将扩展卡尔曼滤波的算法分为两步。第一步为预测:
(4)
式中,Φ=eAΔt。在上面的方程中输入测量值完成预测值计算,然后导入滤波器。
第二步为更新:
(5)
如果选用EKF来估算静压的话,需要建立状态和测量模型来构成滤波器。测量值可以由机载传感器直接获得。
2 相关数学模型
2.1 动力学模型
本文仅对纵向机动进行分析,将与横航向相关的状态作为输入。纵向动力学模型为:
(6)
式中,u,v和w为体轴系上飞机的速度;p,q和r为飞机转动矢量ω在体轴系上的投影;θ和φ为俯仰角和滚转角;ax,ay和az为体轴系上的三向加速度;Ts为外界静温;TISA为标准大气温度;h为几何高度;hp为气压高度;wpi为随机输入噪声;bi为待估计的偏差。
对标准大气,其温度的计算方程为:
TISA=Tsl(1-2.25574212×10-5hp)
(7)
式中,Tsl为海平面标准大气温度;hp的单位为m。该公式在11000 m以下有效。
可以用下式将气压高度转换为静压:
ps=101325(1-2.25574212×10-5hp)5.255863
(8)
式中,ps的单位为Pa。
可以从Kiel管获得精确的总压用于计算校正空速(vc,m/s),公式如下:
(9)
式(6)和式(7)构成了动力学模型的公式。将状态矢量x和输入矢量u定义为:
(10)
其他的输入方程为:
(11)
2.2 测量模型
测量模型是关于测量传感器的模型,需要考虑传感器的类型和校正公式。对于失速速度的测量一般需要考虑以下四个方面的因素:(1)由DGPS测量的速度;(2)由惯导测量的俯仰角;(3)由DGPS测量的几何高度;(4)ADC计算的校正气压高度。值得注意的是,由GPS测得的高度和速度应考虑伪距和多普勒漂移的问题。
测量模型的方程为:
(12)
以上方程中直接的测量参数有3个,wmi为噪声。可以写成矩阵的形式:
Z=[vm,θm,hm,hpm]T
(13)
在确定了动态模型和测量模型后,需要以适当的形式进行EKF滤波。
2.3 增益矩阵
EKF方程允许对模型参数和增益进行同步估算。如假定方程组(6)中的参数为常数,则将其转换为状态方程如下:
(14)
由此,得到增益状态方程为:
xaug=[u,w,θ,h,hp,bax,baz,bq]T
(15)
3 飞行试验及结果分析
为验证该计算方法的可行性,在一架支线飞机上进行了飞行试验。试验机安装了拖锥和Kiel管[2]。在进入失速前飞机保持稳定平飞20 s,然后拉杆减速直至进入自然失速。在失速改出后爬升回原配平高度保持稳定平飞20 s。共试飞了两个架次,一个架次用于验证卡尔曼滤波系数,命名为试验点A;另一个架次采用DGPS综合法,即基于DGPS数据综合计算静压和空速,命名为试验点B。试飞的几何高度变化曲线如图1和图2所示(横坐标S为采样点)。

图1 试验点A几何高度变化Fig.1 Geometric altitude variation for test point A
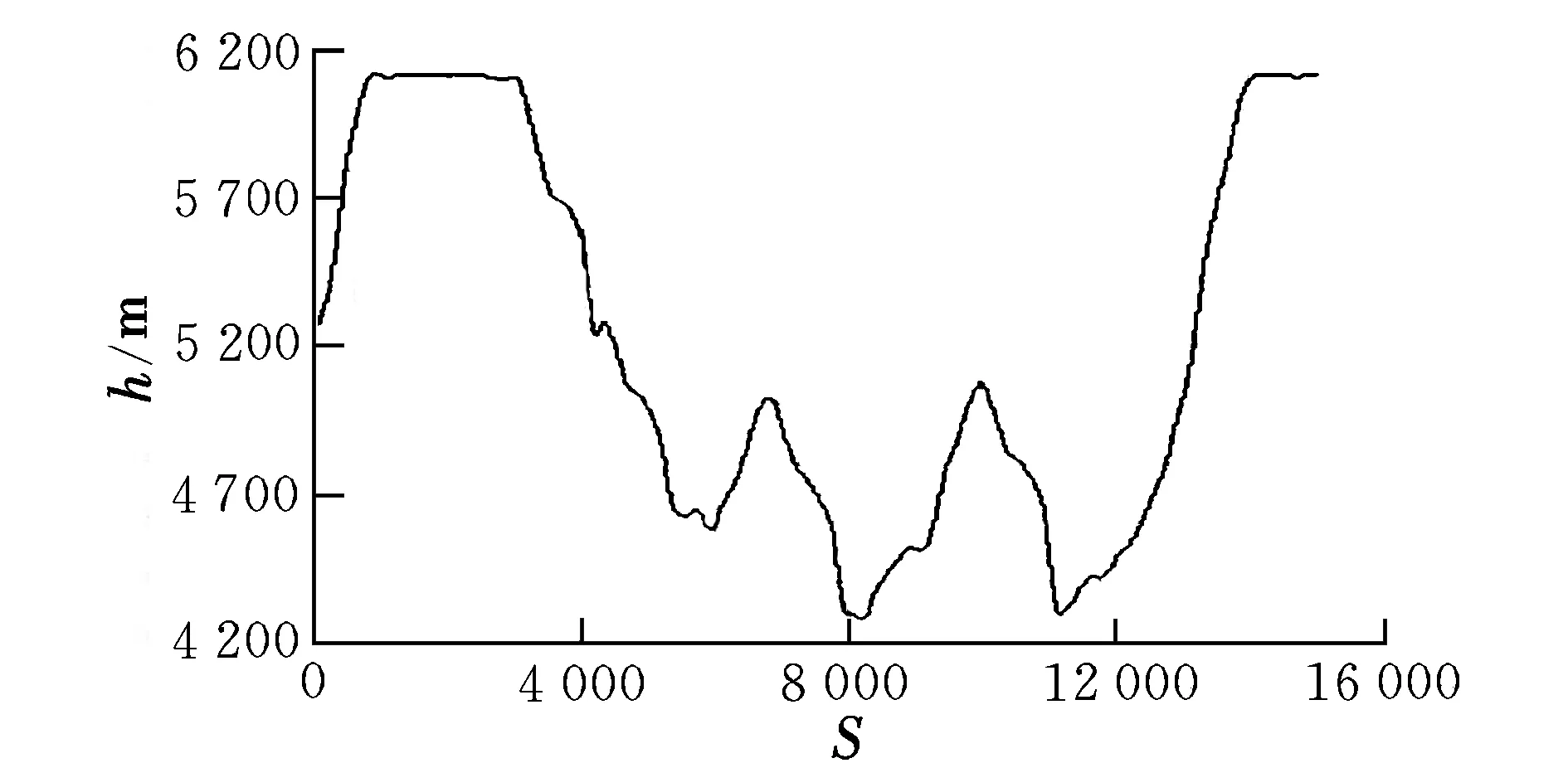
图2 试验点B几何高度变化Fig.2 Geometric altitude variation for test point B
尽管数据采集系统可以提供更高的采样频率,为与DGPS一致采用了每秒钟12.5个样本的采样率。
EKF的相关参数有测量噪声矩阵R和系统随机噪声矩阵Q。测量噪声R通过之前的传感器变化曲线进行计算,Q基于残差和理论分析并与参考方法的结果进行对比。
通过DGPS综合法得到的最小校准空速(CAS)和通过EKF滤波计算得到的结果在表1中进行了对比。两种校准空速的差异很小,绝对值小于0.2 kn或DGPS综合法数值的0.2%。

表1 失速速度结果对比Table 1 Comparison of stall speed results
通过对静压数据进行研究可以进一步分析该方法的可靠性。图3和图4为试验点A和B对应的EKF和ADC测量值相对DGPS综合法的差异。

图3 试验点A压力高度对比Fig.3 Comparison of pressure altitude for test point A

图4 试验点B压力高度对比Fig.4 Comparison of pressure altitude for test point B
图中,卡尔曼滤波法显示出了明显的回归趋势。初始时EKF依据静压测量值进行估算,当滤波器有了足够的数据来提高其预测能力后,其估算值与DGPS综合法的差值减小到了5 m以内。如图所示,经历了2000次采样或160 s后,差值保持小于3 m。在失速阶段ADC静压误差明显较大,接近10~15 m;而同一阶段的EKF估测误差仅1 m左右。
衡量EKF的一个主要指标是各状态参数误差协方差的时间历程曲线。经过卡尔曼滤波后这些误差协方差值均呈指数级递减,变化曲线如图5所示。
滤波器的更新特性意味着滤波器估算传感器测量值的能力,其受限于理论上的方差值“HPHT+R”[3],该方差可以视为高斯白噪声。就本试验而言,滤波器的性能已经足够优化,可以得到较理想的结果。
本文提出的方法可以应用到任何飞机上,但是需要谨慎选择过程和测量噪声协方差矩阵方程,并对滤波器进行适当调整。除使用拖锥外,还有其他有效地进行静压源位置误差校准的方法,如塔侧飞行法或使用DGPS。如果与本文中的方法结合,可以在整个空速校准中避免使用拖锥。
4 结束语
传统的飞机静压源误差校准试验方法在确定飞机失速速度时不够精确,需要对其进行改进。本文提出了一种基于扩展卡尔曼滤波通过计算确定静压,进而得到空速的方法。通过在一架支线飞机上进行实际飞行试验并将该方法的结果与DGPS综合法的结果进行对比,发现该方法的误差在0.2 kn或0.2%以内。说明该方法可以作为一种有效的进行失速速度确定的辅助或替代方法。为得到更高精度的结果可以考虑对更新方程中白噪声作进一步修正。同时,当系统存在较大模型误差和计算误差时,协方差矩阵有可能会产生畸变,容易导致结果发散。如果出现发散,可以考虑采用记忆衰减卡尔曼滤波以抑制滤波发散,提高数据的可靠性。
参考文献:
[1] 张建帆,丁胜,陈军,等.拓展卡尔曼滤波算法在目标跟踪中的改进及应用[J].现代计算机,2012,(32):11-14.
[2] Celso Braga de Mendonca.Aircraft stall speed determination with stochastic filtering approach[C]//39th Annual International Symposium.Texas USA:Society of Flight Test Engineers,2008.
[3] Arthur Gelb.Applied optimal estimation[M].Massachusetts: Massachusetts Institute of Technology Press,1974.

