旋转机翼无人机巡航状态飞行力学模型辨识
王斑, 詹浩, 黄晶
(西北工业大学 航空学院, 陕西 西安 710072)
0 引言
鸭式旋翼机翼无人机兼顾直升机和固定翼飞机的飞行特点,以直升机模式进行起飞、降落以及小速度前飞,以三翼面固定翼模式进行高速巡航[1]。为了兼顾直升机模式和固定翼模式的不同特性,中间旋翼机翼采用椭圆翼型。在飞行过程中,旋翼机翼与机身及后置平尾之间的干扰复杂,很难准确获得飞机的飞行力学模型。
通过传统的方法建立鸭式旋翼机翼无人机的飞行力学模型需要进行大量的测量和风洞试验,这将花费大量的人力、物力,因而是不经济的。为了满足无人机飞行控制系统的设计要求,系统辨识以其简洁、高效、低成本的特点成为传统建模思想的替代方法。并且,由于对无人机进行系统辨识易于开展、成本低廉,所以通过对无人机系统辨识的研究,也可以为其他飞行器飞行力学模型的系统辨识提供经验。
本文主要研究巡航状态下鸭式旋翼机翼无人机飞行力学模型的系统辨识方法。首先通过机理建模建立试验无人机的纵横向通道的参数化模型;然后进行扫频飞行试验,利用频域辨识技术从飞行数据中提取某个通道的线性模型,并从中获得关键参数的值;最后进行时域验证,通过比较模型预测数据和飞行试验数据表明,该模型很好地反映了无人机在巡航状态下的动态特性。该方法和纯机理建模相比,具有易工程化、工作点附近模型准确性高等优点,并且可以基于此模型进行飞行控制系统设计。
1 辨识机理模型建立
系统辨识的一个重要内容就是利用先验知识确定辨识对象的模型结构,辨识模型的结构决定了辨识结果与真实物理系统动力学特性的相符程度,这在很大程度上影响模型拟合的精度和模型的可靠性。
模型选择需要结合该型无人机的飞行特点,选择符合实际飞行动态的模型结构会大大降低辨识的难度,提高模型的精度和可靠性。在飞机设计及控制系统设计初期,通过传递函数可以了解飞机的动态特性及飞机的飞行品质。通过简化可以得到飞机纵、横向传递函数模型[2-3]:
(1)
(2)
式中,Tθ2为分子时间常数;τθ,τφ为时间延迟;Ts和Tr分别为螺旋模态和滚转模态的时间常数。
2 频域辨识算法
根据鸭式旋翼机翼无人机的动力学特性,设计飞行扫频试验,通过对试验数据进行一致性分析和滤波处理得到频域辨识所需的数据[4]。为了减少有限傅立叶变换引起的频谱泄露,使用复合窗函数法对原始试验数据进行处理,之后利用FFT算法将加窗后的数据转换到频域,得到优化的非参数频率响应。通过参数寻优的方法,拟合特定频段内待辨识模型与实测数据的频率响应,得到机理模型中待辨识参数的值。
2.1 基于功率谱密度函数的频率响应估计
典型的飞行器动态响应测量值,如角速率陀螺、加速度计、气动侧滑角和迎角测量值会明显受到来自机械、电子、大气扰动等方面的干扰,这些干扰是输出测量噪声的主要来源。因此认为噪声作用于输出端,并且输入测量不受噪声的干扰,系统的频率响应可用如下功率谱分析方法[5]得到:
H(f)=Gxy(f)/Gxx(f)
(3)
式中,H(f)为输入x与输出y之间的频率响应;Gxy(f)为输入与输出之间的互谱;Gxx(f)为输入数据的自谱。
由于不同通道之间存在耦合,在从输入到输出的系统中存在不能用频率响应H(f)描述的非线性特性、过程噪声和测量噪声的影响。因此引入相干函数,它是判断在频率点f上,输出谱Gyy中由输入谱Gxx线性地引起的部分在整个输出谱中所占的比例,其相干函数表达式为:
(4)
2.2 复合分窗分析
重复的机动首先连接成为串接记录,这些记录分段成为更短的时间重叠记录序列,称为窗口。数据分窗可以降低谱估计中的随机误差。
典型的窗口尺寸选择将在最小有效频率和最大感兴趣的频率ωmax之间提供至少10个数据带宽。最大窗口尺寸通常应限制于单个记录长度的50%。由此可得:
20×2π/ωmax≤Twin≤0.5Trec
(5)
式中,Twin为窗口长度;Trec为单个记录长度。
最终窗口长度的选择是权衡的结果,要兼顾低频增加信息量的需求(需要大窗口)和抑制随机误差的需求(需要小窗口)。本文采用加权的复合窗口法来提高频率响应精度。频率响应估计中的随机误差定义为:
(6)
使用的加权函数[6]为:
Wi=[(εr)i/(εr)min]-4
(7)
式中,(εr)i为该窗口下某频率响应对式(6)的随机误差。最终谱函数的目标函数为:

(8)
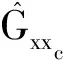
据此将飞行试验扫频得到的数据进行分窗分析,扫频数据为174 s,分别进行5 s,10 s,20 s,25 s,34 s分窗。
2.3 参数化模型辨识


(9)
式中,|·|为每个频率ω处的幅值;∠为每个频率ω处的相位;nω为频率采样点的数量;ω1,ωnω分别为拟合的起始频率值和结束频率值。
代价函数越小说明辨识得到的模型越精确。当代价函数J≤50,则基本可以认为拟合结果相对飞行数据的差异很小。
3 飞行试验设计和辨识结果分析
鸭式旋翼机翼无人机机身上装有一套数据采集系统,其中包括一个三轴陀螺、一个三轴加速度计、一个GPS和一个飞控计算机,数据采样频率为50 Hz。外形如图1所示。

图1 鸭式旋翼机翼无人机Fig.1 The unmanned canard rotor wing aircraft
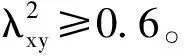
以纵向通道为例,其扫频频率响应和拟合频率响应以及相干函数值如图3所示。在低频及高频区模型与实际测量输出相干性很低。
根据纵、横向通道参数化模型式(1)和式(2),得到鸭式旋翼机翼无人机纵、横向通道传递函数为:



图3 纵向通道频率响应Fig.3 Frequency response of longitudinal channel
4 时域验证
时域验证是评估所辨识模型预测精度和可靠性的重要方法。必须确认模型没有相对该辨识依据的试验数据以及试验飞行条件被过调。为了能较好地验证模型的可信度,输入信号必须和辨识时所选用的输入信号不相似[7]。验证数据采用同一架飞机不同架次的飞行试验数据,并且试验数据相隔时间较短,这样能保证传感器状态等情况相似。
俯仰通道采用类似阶跃的激励信号,如图4所示。滚转通道采用类似双极方波的激励信号,如图5所示。两个通道的时域验证结果如图6、图7所示。可以看出,不论采用何种激励信号,辨识模型预测的响应与飞行试验数据基本吻合,响应趋势基本一致。
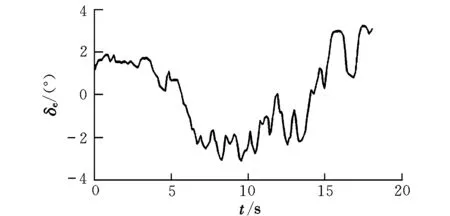
图4 俯仰通道激励信号Fig.4 Excitation signal of longitudinal channel
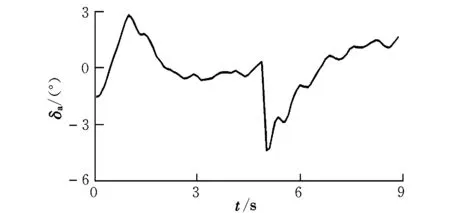
图5 滚转通道激励信号Fig.5 Excitation signal of lateral channel

图6 俯仰角速率的模型预测和实测输出比较Fig.6 Comparison between prediction and practise

图7 滚转角速率的模型预测和实测输出比较Fig.7 Comparison between prediction and practice
通过辨识获得的模型可以计算出飞机各个模态的特征根如表1所示[8]。可以看出,鸭式旋翼机翼无人机具有较大的滚转阻尼和俯仰阻尼,螺旋模态是缓慢发散的,这与实际试飞情况是一致的。

表1 纵、横向通道特征值比较Table 1 Comparison of eigenvalue between longitudinal and lateral channel
综上所述,得到的辨识模型能够很好地预测鸭式旋翼机翼无人机在此飞行条件下的动力学响应特性。辨识得到的传递函数是正确和可信的,可以用于无人机品质分析以及增稳控制系统设计。
5 结束语
本文首先采用机理建模方法确定了鸭式旋翼机翼无人机巡航状态下纵、横向的传递函数模型,然后利用飞机纵、横向扫频飞行试验数据及频域辨识技术确定了待辨识模型的参数。通过时域验证表明,模型预测的响应与飞行试验数据基本吻合,证明了本文所建立的辨识方法是正确可行的;对后续鸭式旋翼机翼无人机其他飞行模态的辨识工作有一定的借鉴价值,对分析鸭式旋翼机翼无人机飞行品质以及增稳控制系统设计具有指导意义。
参考文献:
[1] Mitchell C A,Vogel B J.The canard rotor wing(CRW) aircraft—a new way to fly[R].AIAA-2003-2517,2003.
[2] Tischler M B.Identification and verification of frequency-domain models for XV-15 tilt-rotor aircraft dynamics in cruising flight[J].Journal of Guidance,Control,and Dynamics,1986,9(4):446-452.
[3] Eggleston J M,Mathews C W.Application of several methods for determining transfer functions and frequency response of aircraft from flight data[R].Langley Field,Va:NACA TN 2997,1953.
[4] Tischler M B,Kaletka Jurgen. Modeling XV-15 tilt-rotor aircraft dynamics by frequency and time-domain identification techniques [R].Technical Report TM-89404,NASA,Moffett Field,CA,1986.
[5] Tischler M B,Remple R K.Aircraft and rotorcraft system identification:engineering methods with flight test examples[M].Blacksburg,Virginia:AIAA,2006:145-164.
[6] Strang G.Linear algebra and its applications[M].New York:Academic Press,1980:180-190.
[7] Theodore C R,Tischler M B,Colbourne J D.Rapid frequency-domain modeling methods for unmanned aerial vehicle flight control applications[J].Journal of Aircraft, 2004,41(4):735-743.
[8] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:288-346.

