高超声速滑翔飞行器多目标再入轨迹优化
任洋, 曹林平, 国海峰, 丁达理
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
0 引言
近年来,物理规划方法[1]在解决多目标优化问题上显现出较大的优势,特别是它能够根据设计者的偏好,得出合理的折中解。胡丹等[2]利用物理规划解决了数据中继卫星链路多目标配置决策问题,但对各项指标的产生办法没有做出解释。龙琼等[3]利用物理规划对路径诱导问题进行了定量描述,通过与A*算法的结合将路径决策与驾驶者的偏好结合起来。雍恩米等[4]运用物理规划解决了高超声速滑翔飞行器再入轨迹优化问题,但其运动学模型只考虑了二维平面,没有考虑地球自转,相对简单,且采用遗传算法作为优化算法,若要达到较高寻优精度,所需运算时间相对较长。
本文以高超声速滑翔飞行器三维再入段轨迹优化为研究对象,运用了hp自适应伪谱法,在物理规划的框架下对多目标再入轨迹进行了寻优;针对hp自适应伪谱法的寻优特点,对物理规划框架的偏好函数进行了改进,增大了其适用范围;对不同偏好的再入段最优轨迹进行了仿真对比,为优化方案选择提供了参考。
1 三自由度再入轨迹数学模型
飞行器再入轨迹数学模型包括飞行器三自由度动力学模型和气动力模型。
1.1 飞行器动力学模型
考虑地球为旋转圆球的三自由度再入运动模型为:
(1)
式中,r为地心距;θ为经度;φ为纬度;V为速度;γ为航迹角;ψ为航向角;ω,g,β,L,D分别为地球自转角速度、引力加速度、侧倾角、升力和阻力。
1.2 气动力模型
在高超声速飞行器再入过程中,要通过临近空间穿过大气层到达指定空域,而临近空间大气环境变化复杂,需对气动模型进行较为精确的拟合。飞行器受到的升力L和阻力D的计算公式如下:
(2)
式中,S为气动参考面积;ρ为大气密度;升力系数CL(α,Ma)和阻力系数CD(α,Ma)的表达式为:
(3)
式(3)中的系数l(j),d(j)通过对X-33飞行数据进行拟合得到[5],如表1所示。
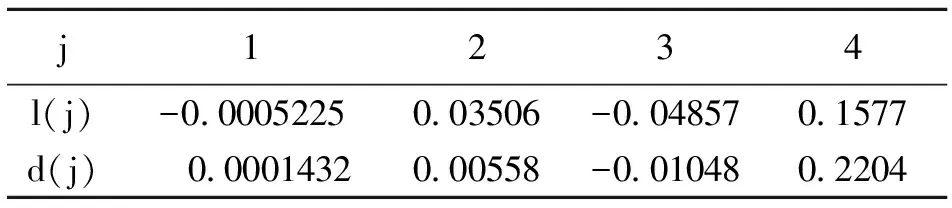
表1 l(j),d(j)的数值Table 1 The value of l(j),d(j)
本文中的大气密度计算公式用指数大气模型来近似代替:
ρ=ρ0e-h/H
(4)
式中,ρ0为海平面的大气密度;高度h=r-R0,R0为地球平均半径;H为标量高度系数。
1.3 约束条件
(1)终端约束
本文中再入终端约束包括高度、经度、纬度和速度约束,相关约束条件为:
h(tf)=hf,θ(tf)=θf
φ(tf)≥φf,V(tf)≥Vf
(2)热流、过载、动压约束
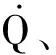
(5)
1.4 优化目标
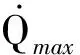
f1=min(tf)
f2=max(δ)=max|φf-φ0|
1.5 轨迹优化问题描述
轨迹优化问题实际上是最优控制问题,在满足各种约束条件下,寻求使某个指标最优的控制量。高超声速飞行器再入轨迹优化可以归结为如下最优控制问题:
(6)
式中,状态变量X(t)=[r(t),θ(t),φ(t),V(t),γ(t),ψ(t)];控制变量U(t)=[α(t),β(t)];路径约束为C[X(t),U(t),t]。
伪谱法在求解单目标轨迹优化问题时显现出很大的优势。本文采用hp自适应伪谱法作为轨迹寻优方法,hp自适应伪谱法的特点是运算所需时间较短,能够通过决定在某个网格时间区间中的状态量和控制量是否满足特定的偏差来调整当前的计算方式,以达到提高算法精度的目的。如果没有满足精度要求,则配置点的数目及分配方式要通过增加多项式的阶数或者更新网格来达到精度要求,具体算法参见文献[6-7]。
2 物理规划方法概述
2.1 设计思路
物理规划[1]是Messac提出的一种处理多目标优化设计问题的有效方法,是处理多目标优化问题的新框架。其基本思路是:通过求解单目标优化问题,确定区间边界,从而建立偏好函数,将不同物理意义的各种设计目标转换为具有相同数量级的无量纲的综合满意度目标,再对综合满意度目标进行优化,寻求使其最优的设计点,即为最优解。
2.2 数学模型
物理规划的决策模型为:
(7)
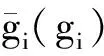
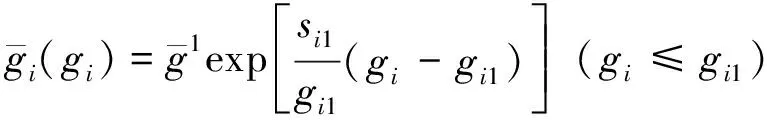
(8)
(9)
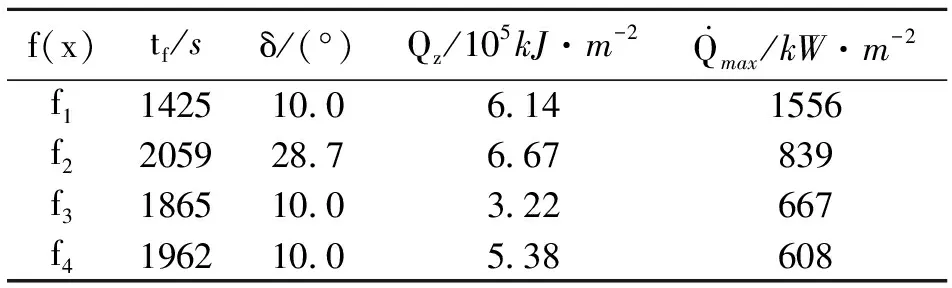
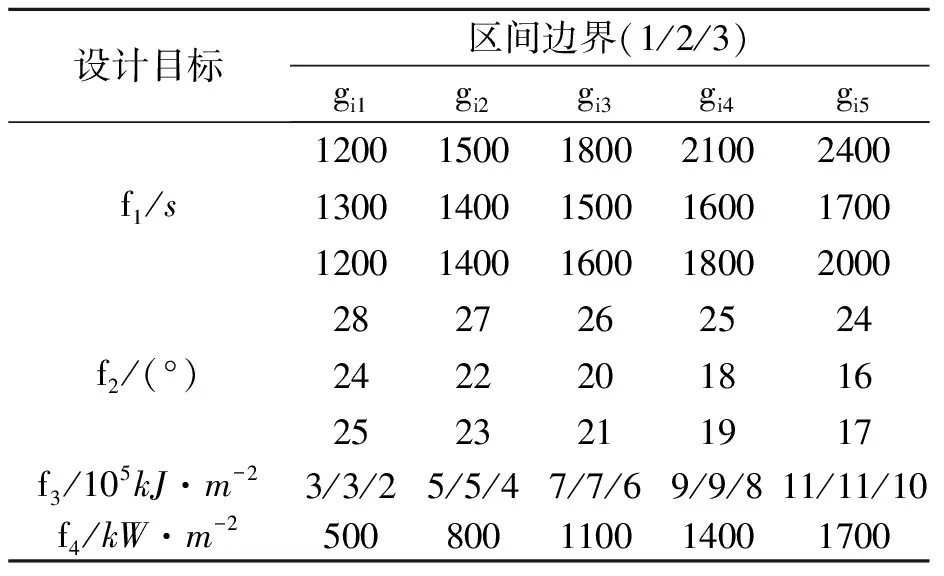
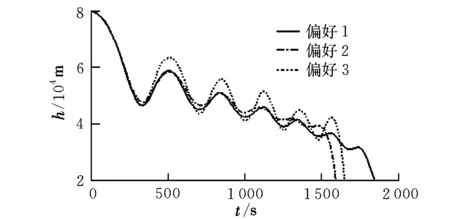
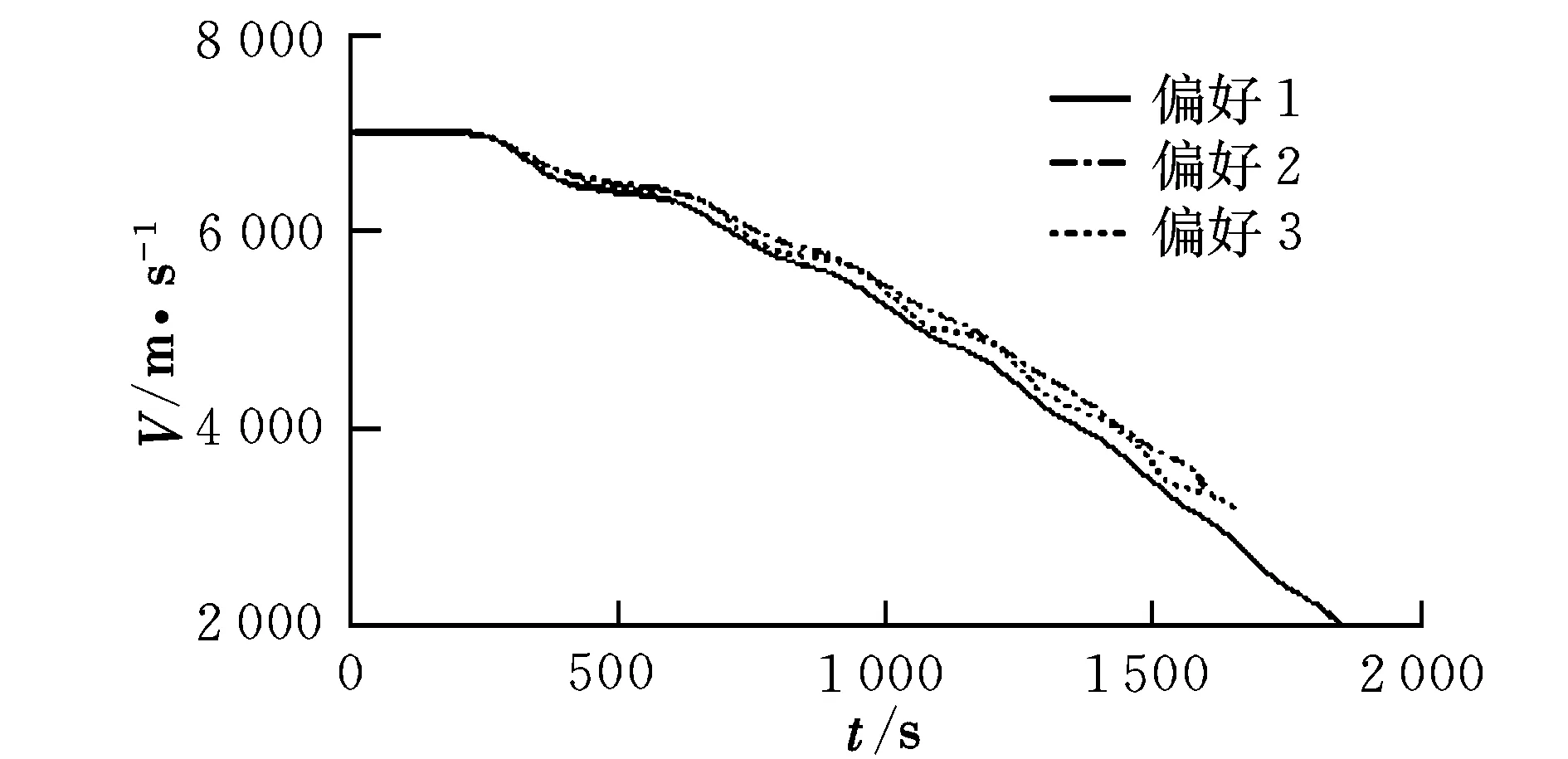
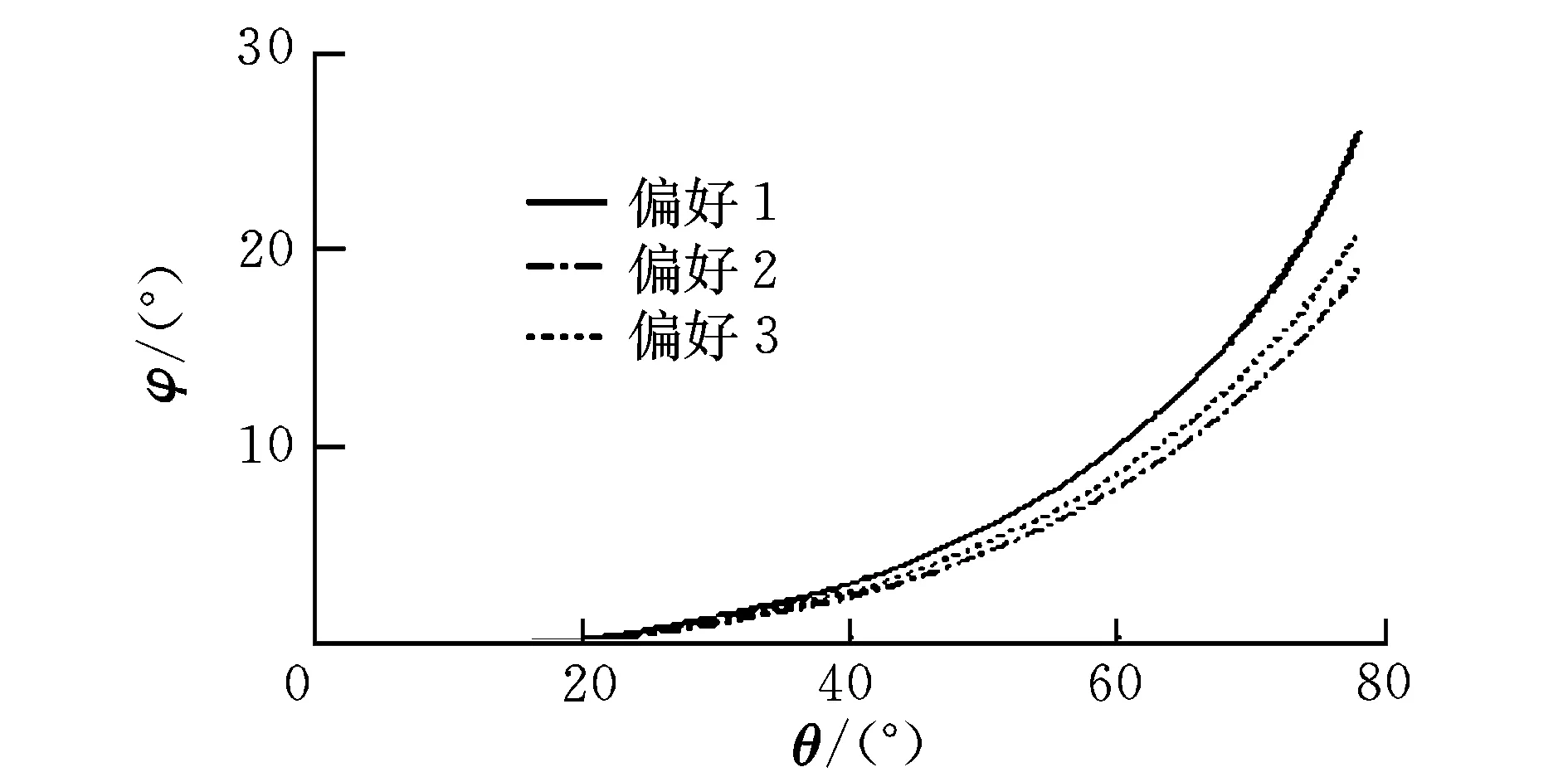
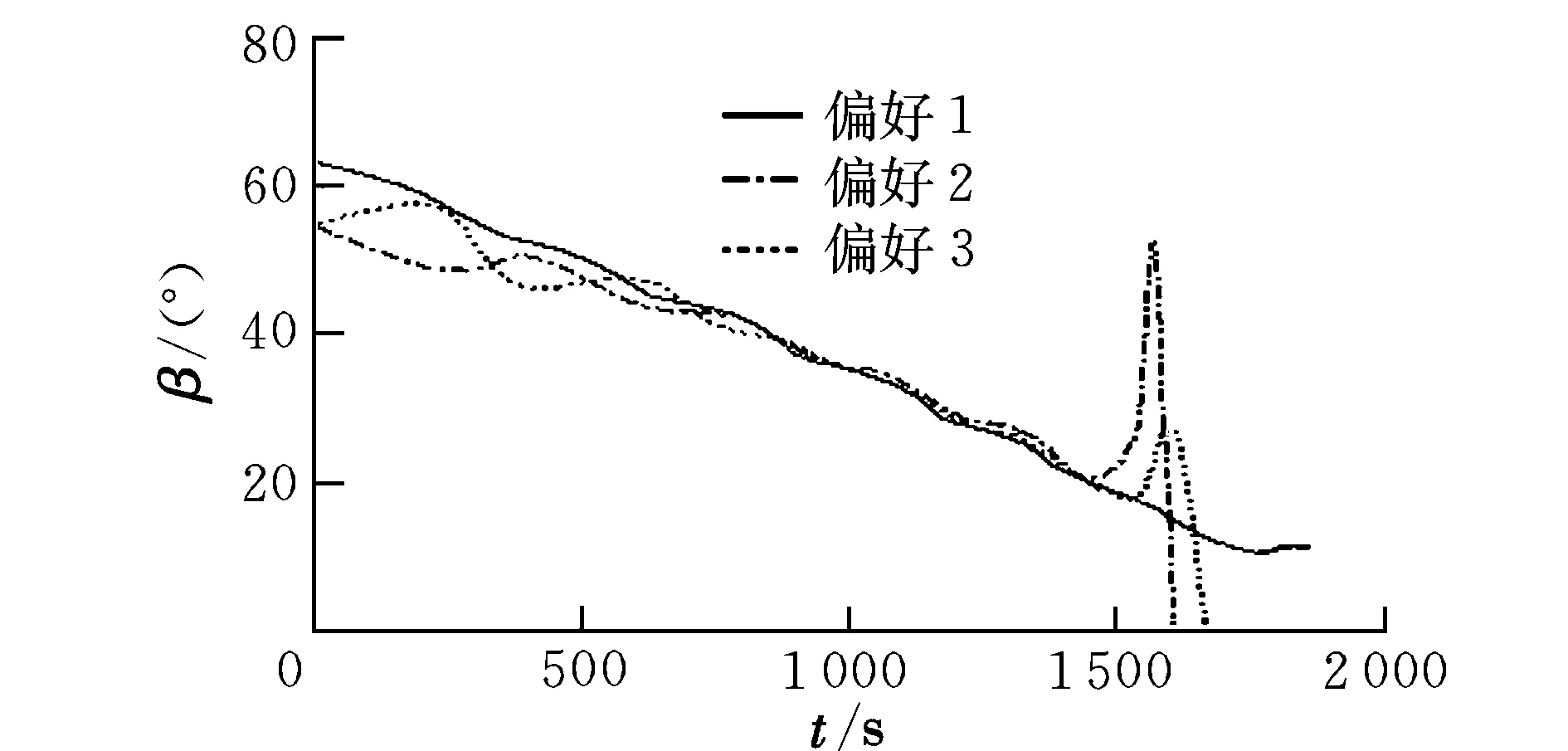
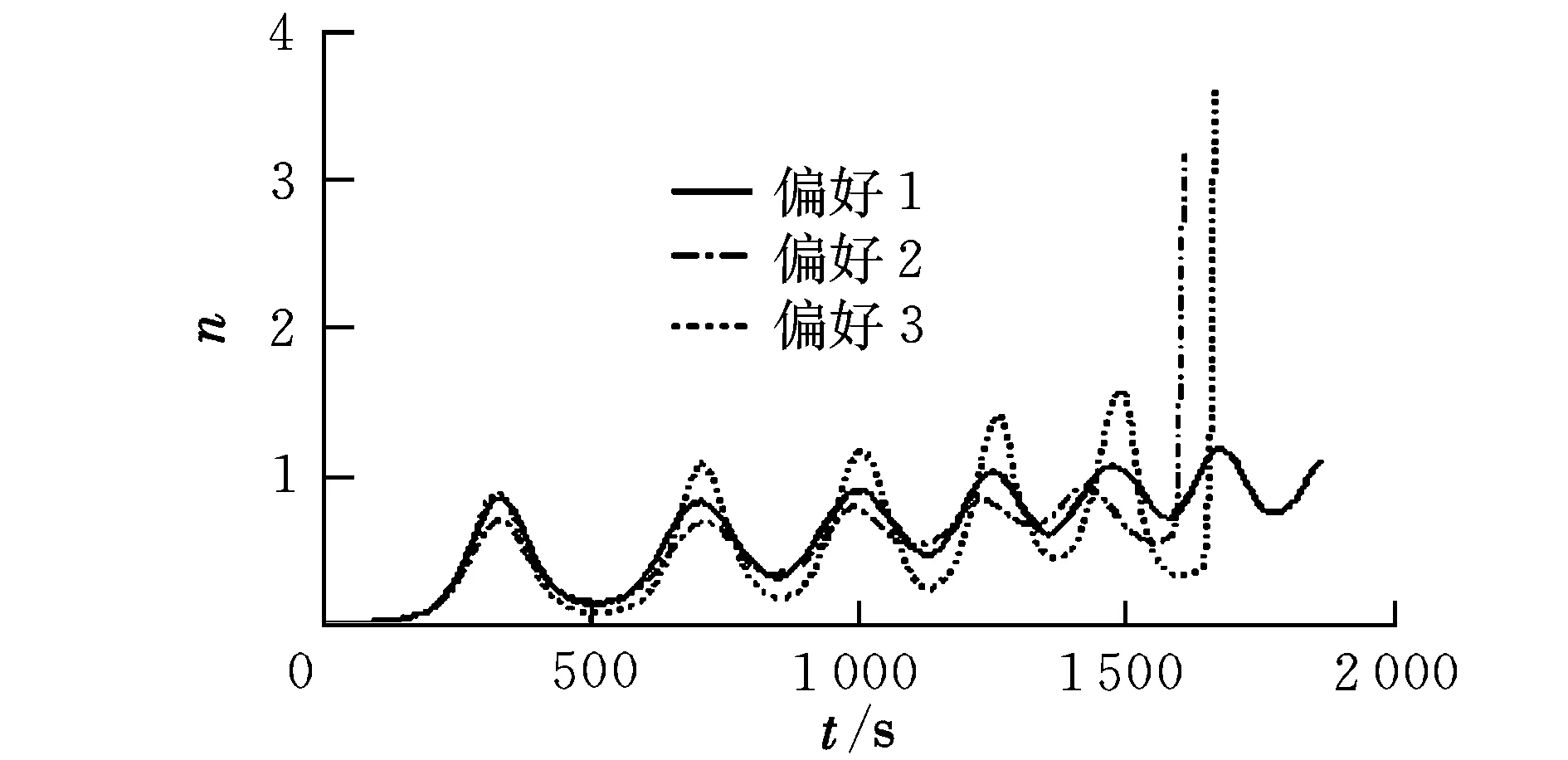
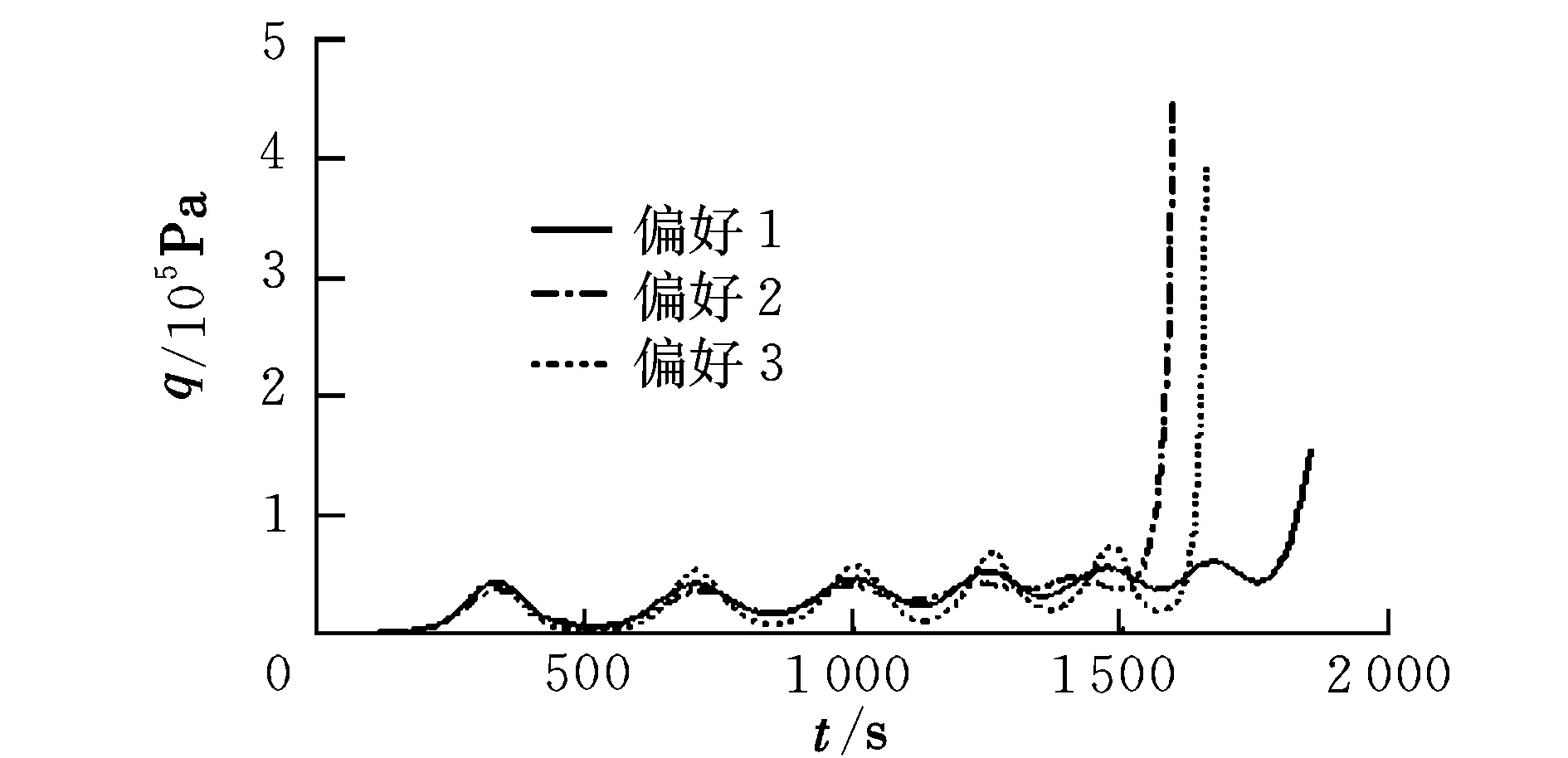
式中,gi(k-1) (10) λik=gik-gi(k-1) (11) (12) (13) (14) (15) 区间端点信息确定方法如下: (16) 构造偏好函数时,需要验证其是否满足二阶导数严格为正的特性,即对区间边界处的二阶导数进行验证,可由式(17)计算得出。 (17) 其中: (18) (19) 由于0≤ξik≤1,所以只需要验证a,b是否为正即可[2]。 (20) 由1.4节中确定的优化目标可知,偏好仅为Class1-S型和Class2-S型,其优化模型的综合满意度目标为: (21) 首先运用hp自适应伪谱法求解出单目标情况下的最优轨迹,利用得到的各目标参数确定物理规划偏好区间边界,建立物理规划框架。然后将物理规划优化模型的代价函数作为hp自适应伪谱法的寻优目标进行寻优,即将每次循环得到的各单目标值带入物理规划框架,得到综合满意度目标,对综合满意度目标进行寻优,得到最优解。这样就将多个目标轨迹优化问题转换为一个反映设计者偏好的单目标问题。具体流程如图1所示。 图1 算法流程图Fig.1 Flow chart of the algorithm 取飞行器质量m=907 kg,气动参考面积S=0.48 m2,初始再入点高度h=80 km,初始经度θ0=0°,初始纬度φ0=0°,初始速度V0=7000 m/s,初始航迹角γ0=0°,初始航向角ψ0=0°,设定最终高度hf=20 km,最终经度θf=78°,最终纬度φf≥10°,最终速度Vf≥2000 m/s。 状态变量及控制变量的约束条件如下: 为确定物理规划问题的偏好结构,首先求解和分析单目标最优轨迹。运用hp自适应伪谱法,分别以各单目标为优化目标寻优,可得到当满足某单目标最优时其余目标的数据如表2所示。 表2 单目标最优时其余目标对应值Table 2 Data corresponding to the rest when single objective is optimum 由于再入过程中各中间变量存在着较强的耦合关系,不存在使所有目标同时最优的设计点。通过对其整体分析可以看出,追求单个目标最优时,容易出现其他指标太过局限的情况,实用性不大。 根据相关约束的边界条件及表2计算结果,确定三组区间边界不同的偏好结构,记为偏好1,2和3,分别对应于期望横程较大、再入时间较短和总气动加热较小的三组偏好,如表3所示。 表3 多目标轨迹优化的偏好结构Table 3 Preference structure of multi-objective trajectory optimization 为作对比,本文分别采用hp自适应伪谱法和文献[4]中算法对该问题进行寻优,设定精度为10-5。 (1)优化结果对比 根据表3中的三组偏好结构,采用两种算法,得到的三组目标函数分别对应横程较大、再入时间较短、总气动加热较小。 本文算法所需运算时间分别为12.32 s,12.20 s,11.79 s。三组偏好函数为: f1=(1854 s,26.0°,6.48×105kJ/m2,844 kW/m2) f2=(1601 s,19.0°,6.49×105kJ/m2,794 kW/m2) f3=(1660 s,21.1°,6.05×105kJ/m2,859 kW/m2) 文献[4]算法所需运算时间分别为66.47 s,69.55 s,56.06 s。三组偏好函数为: f1=(1842 s,25.9°,6.48×105kJ/m2,846 kW/m2) f2=(1596 s,18.9°,6.48×105kJ/m2,789 kW/m2) f3=(1662 s,21.1°,6.07×105kJ/m2,861 kW/m2) 对比可知,两种算法所得各组目标函数均能体现出设计者的偏好,且各项设计指标都在可接受的范围内,是各目标之间相互妥协折中的反映,避免了因追求单个目标最优而出现的其他指标太过局限的情况。但本文算法在所需寻优时间上有明显优势,更接近于在线实时规划;验证了改进的物理规划方法的有效性,使其可在不改变约束边界值的情况下,增大适用范围。 (2)再入过程分析 对本文算法所得优化结果进行分析,最优轨迹及相应的控制变量、过程约束量如图2~图9所示。通过对比分析可以发现: ①在要求总气动加热较小时,高超声速滑翔再入轨迹的振荡幅值较大,即通过大幅振荡来减少动能和势能向热能的转换,但此时对飞行器机体结构要求较高。 ②当设计者要求较短时间再入时,飞行器为快速再入到指定高度,在很长一段时间内保持了较大的再入速度;末端迎角快速减小,导致飞行末端动压较大,同时引起其他变量的一系列大幅调整;对比三组偏好可发现,随着末端速度的减小,末端动压逐渐回归到较好的范围内。 ③初始下降段一般采用较大的迎角减速,对比图6可以看出,要求总气动加热较小时,初始段迎角平均值较其他偏好大,以增大振荡幅度;末端迎角大幅变小,以较快进入指定高度。 ④初始段倾侧角较大,以快速改变再入方向,增大横程;随着速度的减小,倾侧角逐渐减小,这是由于要兼顾纵程和再入时间,不能因为追求横程而使纵程过小或者再入时间太长;末端由于迎角的调整,倾侧角有相应的振荡变化,使末端再入过程满足过载、热流等约束。 图2 高度变化曲线Fig.2 Altitude variation curve 图3 速度变化曲线Fig.3 Velocity variation curve 图4 横程变化曲线Fig.4 Cross-range variation curve 图5 迎角变化曲线Fig.5 AOA variation curve 图6 倾侧角变化曲线Fig.6 Bank angle variation curve 图7 过载变化曲线Fig.7 Load variation curve 图8 动压变化曲线Fig.8 Dynamic pressure variation curve 图9 热流密度变化曲线Fig.9 Variation curve of heat flow density 本文对高超声速滑翔式再入飞行器三自由度最优轨迹进行了研究,在物理规划的框架下,对期望横程较大、再入时间较短以及总气动加热较小的三组偏好进行了仿真,验证了改进的物理规划方法与伪谱法结合求解多目标优化问题的有效性,得到了反映设计者偏好且实用性更强的三组折中解,所需优化时间相对较短,具有实时应用潜力,可为再入轨迹的优化选择提供一定借鉴。 参考文献: [1] Messac A.Physical programming-effective optimization for computational design[J].AIAA Journal,1996,34(1):149-158. [2] 胡丹,闫忠文.基于物理规划的数据中继卫星链路配置决策方法[J].中国空间科学技术,2009,10(5):54-60. [3] 龙琼,胡列格,张蕾,等.基于物理规划的路径诱导方法[J].中南大学学报(自然科学版),2012,43(8):3287-3293. [4] 雍恩米,唐国金,陈磊.基于物理规划的高超声速飞行器滑翔式再入轨迹优化[J].航空学报,2008,29(5):1091-1097. [5] Bollino Kevin P,Michael Ross,Doman David D.Optimal nonlinear feedback guidance for reentry vehicles[R].AIAA-2006-6074,2006. [6] Darby C L,Hager W W,Rao A V.An hp-adaptive pseudospectral method for solving optimal control problems[J].Optimal Control Applications and Methods,2011,32(4):476-502. [7] 国海峰,黄长强,丁达理,等.多约束条件下高超声速导弹再入轨迹优化研究[J].弹道学报,2013,25(1):10-15.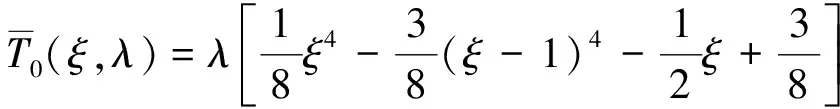
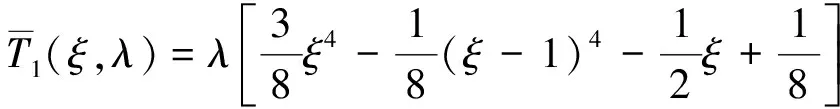
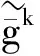
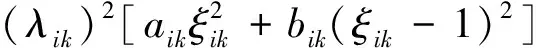
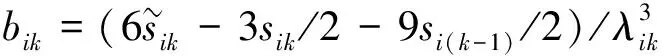
2.3 算法改进
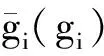

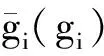
3 算法流程

4 仿真结果及分析
4.1 初始条件
4.2 偏好结构的确定
4.3 优化结果及分析


5 结束语

