平流层飞艇滑模姿态控制系统设计
王领, 郭建国, 周军, 王国庆
(1.西北工业大学 精确制导与控制研究所, 陕西 西安 710072;2.中国运载火箭技术研究院 研究发展中心, 北京 100076)
0 引言
随着对临近空间飞行器研究的不断深入,平流层飞艇越来越受到世界各国的重视[1-2],其控制技术也成为研究的热点。针对平流层飞行环境所带来的特殊问题,以及飞艇自身的飞行控制特性,不少学者开展了平流层飞艇的姿态控制技术研究。文献[2]针对平流层环境,较为详细地提出了飞艇的总体结构和动力学建模,并给出了控制方案;文献[3]针对一种自主飞艇提出动力学建模方法;文献[4]应用输入输出反馈线性化的控制方法设计了飞艇姿态鲁棒控制系统;文献[5]基于神经网络和变结构控制相结合方法设计了鲁棒自适应飞艇控制系统。
针对飞艇在平流层实现定点驻留的任务需求,同时考虑到在平流层飞行的特殊飞行环境中飞艇姿态所产生的通道耦合和不确定性,本文应用反演法[6]来设计动态的滑动模态,以抑制不确定性对姿态的影响,同时也避免了反演法的微分膨胀问题。通过两个滑动平面的设计,利用Lyapunov稳定理论,设计了一种新的飞艇姿态控制系统,实现了飞艇姿态的稳定控制,并通过数学仿真证明了设计方法的有效性。
1 飞艇姿态控制系统模型
平流层飞艇的姿态动力学模型可借助文献[2]中给出的非线性姿态动力学模型的建模方法。不失一般性,这里仅考虑俯仰通道姿态动力学模型,该模型不仅考虑到平流层飞行环境对飞艇姿态产生了许多不确定性因素,而且还包含了飞艇的建模误差和通道耦合。平流层飞艇俯仰通道姿态非线性动力学模型为[3]:
(1)
式中,θ,φ分别为俯仰角和滚转角;q,r和p分别为绕艇体各轴的角速度分量;Ix,Iy,Iz分别为x,y,z轴向的转动惯量;Ixz为惯性积;zG,xG为重心在艇体坐标系下的坐标;u,v和w分别为沿艇体各轴的速度分量;M1为除气动舵面之外产生的其他力矩;aδz为气动舵面控制力矩,a为飞艇的气动控制力矩系数。
这里不采用线性化的建模方式,直接针对非线性模型(1),令x1=θ,x2=q,u=δz,则模型(1)可写为:
(2)
其中:
b=a/Iy,d=x2(cosφ-1)-rsinφ
f(x)= -[(Ix-Iz)pr+Ixz(p2-r2)+
pv-qu)-M1]/Iy
2 非线性姿态控制系统设计
为了使飞艇俯仰通道获得姿态稳定,这里总体上采用变结构控制方法,在滑动模态上,基于反演法设计自适应的动态滑模,来设计飞艇的姿态控制系统。
设俯仰通道的指令姿态角为θm,则俯仰角跟踪误差为:
e=x1-θm
(3)
选择第一个滑动模态为:
s1=e
(4)
选择:
(5)
式中,k1>0;ε1>|d|。由此,可得虚拟控制:
x2m=-k1s1-ε1sgn(s1)
(6)
为了避免虚拟变量x2m的直接微分,设计一阶动态滤波器:
(7)
式中,τ>0。再选择第二个滑动模态为:
s2=x2-x2c
(8)
选择:
(9)
式中,k2>0;ε2大于通道间的未知耦合量的大小。可得姿态控制律:
(10)
由此可得以下定理:
定理1:针对给定的平流层飞艇姿态控制系统(1),如果控制律采取式(10),则在有限时间内飞艇姿态系统中俯仰角达到稳定,并具有一定的鲁棒性。
显然为了说明姿态系统的稳定性,可分别取Lyapunov函数为:
(11)
或
(12)
由式(5)可得飞艇姿态系统中俯仰角在有限时间内收敛到期望角度。只要式(5)成立和式(9)中ε2满足大于通道间的未知耦合量的大小条件,则飞艇姿态控制系统具有一定的鲁棒性。
此外,考虑到变结构控制律(10)含有不连续的符号函数,用饱和函数代替即可,控制律变为:
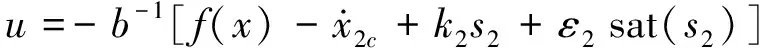
(13)
3 数学仿真及分析
为了说明所设计的飞艇姿态控制系统的有效性,以文献[2]提供的平流层飞艇数据为例,采用本文设计的滑模姿态控制系统进行数学仿真[7]。考虑飞艇的飞行高度为21 km,环境风速为20 m/s,飞艇初始姿态角均设为1°,同时设定期望的俯仰角为3°。具体仿真参数设定为:k1=0.1,ε1=1,k2=0.1,ε2=1,τ=0.1。
飞艇在俯仰通道上的俯仰角和舵面偏转角的变化曲线如图1和图2所示。从图1中可以看出,俯仰角在80 s内逐渐收敛并接近3°,由于存在一定的测量误差,最终俯仰角误差在0.5°之内;从图2中可以看出,采用式(13)的变结构控制律,可以有效地削弱原来变结构控制中固有的振荡问题。
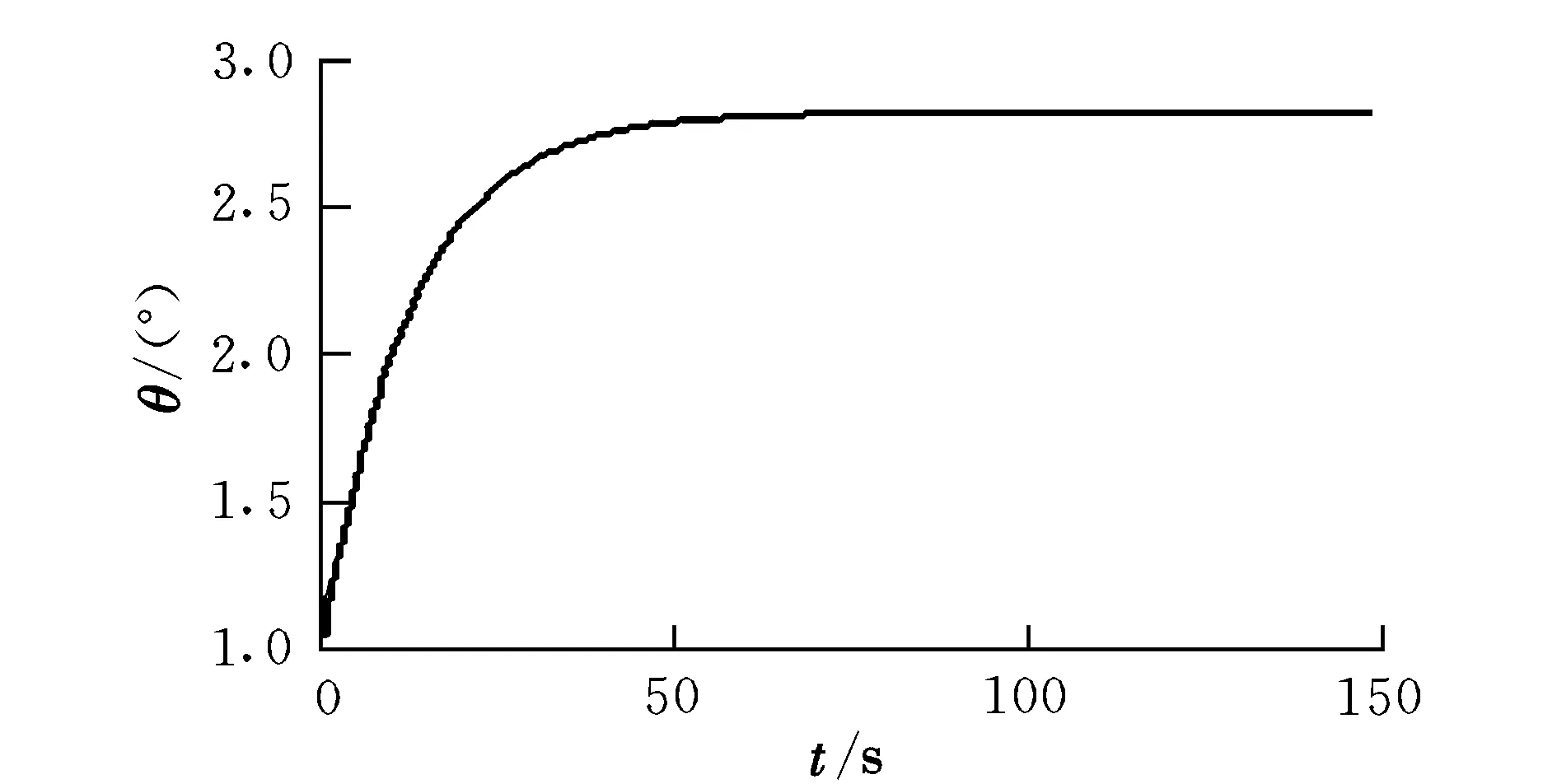
图1 俯仰角响应曲线Fig.1 Behaviour of pitch angle

图2 舵面控制指令Fig.2 Command of control surface
此外,从整个飞艇姿态所获得的其他通道的仿真结果和俯仰通道的情况相一致,因此,采用反演法和变结构相结合的姿态控制系统,能够使飞艇适应平流层环境和内部结构参数的影响,并实现良好的跟踪控制效果。
4 结论
本文针对平流层飞艇设计了鲁棒的非线性姿态控制,得到以下结论:采用反演法和变结构设计的动态滑模可以有效地解决飞艇在平流层飞行环境中所存在的不确定性因素,实现姿态的稳定,具有良好的鲁棒性。可以将该方法应用于飞艇的定点控制中,便于工程实现。
参考文献:
[1] Eguchi K,Yokomaku Y,Mori M.Feasibility study program on stratospheric platform airship technology in Japan [R].AIAA-1999-3912,1999.
[2] Joseph B M,Michael A P,Zhao Yiyuan.Development of an aerodynamic model and control law design for a high altitude airship[C]//AIAA 3rd Unmanned Unlimited Technical Conference,Workshop and Exhibit.Chicago,2004:415-431.
[3] Cai Z L,Qu W D,Xi Y G.Dynamic model for airship equipped with ballonets and ballast[J].Applied Mathematics and Mechanics,2009,26(8):1072-1082.
[4] 王晓亮,单雪雄.平流层飞艇姿态鲁棒控制研究[J].系统仿真学报,2006,18(5):1271-1274.
[5] 郭建国,周军.基于滑模神经网络的自主飞艇姿态控制[J].飞行力学,2009,27(1):40-42.
[6] Zhang T,Zhu Q,Yang Y.Adaptive neural control of non-affine pure-feedback nonlinear systems with input nonlinearity and perturbed uncertainties[J].International Journal of Systems Science,2012,43(4):691-706.
[7] 刘金琨.滑模变结构控制Matlab仿真[M].北京:清华大学出版社,2005:251-255.

