一种无人机气动参数辨识的实现方法
李寒冰, 吴大卫
(中国商用飞机有限责任公司 上海飞机设计研究院, 上海 201210)
0 引言
研制高性能无人机需要建立其飞行动力学模型,它是无人机控制系统设计与调校、飞行仿真及飞行品质评价的重要前提和基础,而获得准确的各项气动导数是成功建模的关键。
目前无人机的气动导数主要用以下两种方法求得:一种是理论计算法,采用传统工程估算和现代计算流体力学技术,但在计算精度、建模准确程度以及求解时间上往往难以兼顾;另一种是试验法,包括风洞试验法和参数辨识试验法。其中风洞试验法的缺点在于试验周期较长,成本较高。参数辨识试验法是以飞行试验测得的状态数据作为飞行动力学参数化方程的输入输出数据,选择合适的辨识方法在仿真环境下经过有限次迭代得到参数模型中未知参数的值。辨识结果能真实反映无人机的本身属性,因此成为求取无人机气动导数的一种有效手段[1-2]。
本文以某小型飞翼无人机为例,针对飞行试验测量条件有限,提出了一种根据可测数据估算迎角、侧滑角和气动系数的方法,从而得到完整的飞行数据用于无人机气动参数辨识中,并验证了该方法的有效性。
1 飞行试验限制及数据完善
1.1 小型无人机飞行试验的特点
相比有人驾驶飞机,无人机采用了不同的控制系统和配套机载设备,在飞行试验中表现出技术风险高、调控难度大、信息处理复杂、气动参数测量困难等[3-4],而对于小型无人机而言又具有自身承载能力小的特殊性。
反映无人机系统动态特性的参数有:线位移、线位移速度和加速度、角位移、角速度和角加速度等。一般可利用大气数据传感器、惯性测量单元和无线定位天线等设备测量和采集记录上述数据。但是,在缺少气动角数据的情况下,还不足以对无人机的气动参数进行辨识。气动角包括迎角和侧滑角,主要采用压差归零和风标式传感器进行测量[5]。而对于小型无人机的重量和尺寸限制,这些测量装置难以在保证精度的条件下实现同步小型化和轻量化,使小型无人机气动参数辨识工作难以展开。
1.2 迎角和侧滑角的估算方法
在现有试验条件下,可以测得体轴系下三轴过载nx,ny,nz和空速V的准确值。动坐标系下的加速度方程[6]为:
dV/dt=δVB/δt+ωVB
(1)
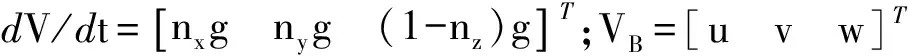
方程(1)写成体轴系标量形式,即:
(2)
本文采用四阶龙格库塔算法求解常微分方程组(2),可得到体轴系速度分量u,v,w关于过载nx,ny,nz和角速率p,q,r试验数据的数值解。解得体轴系速度分量并与空速测量值V联立可得迎角和侧滑角:

(3)
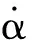
上述方法弥补了试验条件的不足,合理地估算了迎角和侧滑角这两个重要参数,完善了飞行数据,为无人机气动参数辨识提供了可行性。
1.3 方法适用范围
上述估算迎角和侧滑角的方法是在无人机试验条件有限、无法测得准确气动角的情况下提出的一种完善飞行数据的简化方法。试验证明,在无风或微风的飞行条件下,该方法所得估算结果能够很好地再现气动角的响应历程。另外,由于辨识模型使用了实际的飞行数据作为辨识输入输出数据,无需复杂的推导,具有通用性。因此,上述完善辨识试验数据的方法对其他布局形式的固定翼无人机也是普遍适用的。本文还采用三轴过载试验数据估算气动系数,详见下文。
2 研究对象和飞行试验设计
2.1 研究对象
本文以某小型飞翼布局无人机为研究对象(见图1),其基本参数如表1所示。

图1 用于飞行试验的飞翼无人机Fig.1 The flying wing UAV for flight test

机长L/m翼展b/m起飞质量WTO/kg有效载荷WPL/kg续航时间t/min1.21.761.545
飞机弹射起飞后采用人工对飞机姿态进行调整控制,完成配平后输入激励指令。飞行数据通过机载设备记录并传输给地面站。采集的数据主要包括:副翼偏角δa、升降舵偏角δe、姿态角(滚转角φ、俯仰角θ、偏航角ψ)、角速度(滚转角速度p、俯仰角速度q、偏航角速度r)、过载(nx,ny,nz)、空速V、气压高度H、升降速率、GPS速度和高度、航向及经纬度等。
飞行试验选择在初冬进行,微风无持续风向,低空飞行可近似视为无风条件。
2.2 飞行试验设计
飞行试验中需要充分激发飞机的各种运动模态,获取足够的信息量用于气动参数辨识。
常用的激励信号有阶跃输入、脉冲输入、偶极方波输入、3-2-1-1输入等。对于本文的研究对象而言,阶跃输入可能会导致飞机向某一方向偏离,对飞行安全不利;脉冲输入在实际应用中难以实现,而且由于舵机速率限制,过快的脉冲输入往往不能激励飞机的飞行模态;3-2-1-1输入信号的时间历程远远超过了飞机的短周期时间历程,因而无法激励飞机的短周期模态。因此,本文采用偶极方波输入,其数学模型为:
(4)
该信号频谱密度较宽,在高频区域也含有能量,适当调整Δt可以在感兴趣的模态频段含有足够的能量,且克服了其他信号的使用限制,是个简单而有效的输入信号[2,7]。
3 纵向参数辨识
3.1 迎角计算结果
在飞机纵向气动参数辨识试验中,对升降舵进行偶极方波激励,为了方便与正负过载对应,本文取拉杆时升降舵偏角为正值。
试验可以测得体轴系下三轴过载nx,ny,nz和空速V的准确值,由式(1)~式(3)可以得到迎角α的估算值。图2为升降舵偶极方波激励及其对应的α的响应曲线估算结果。
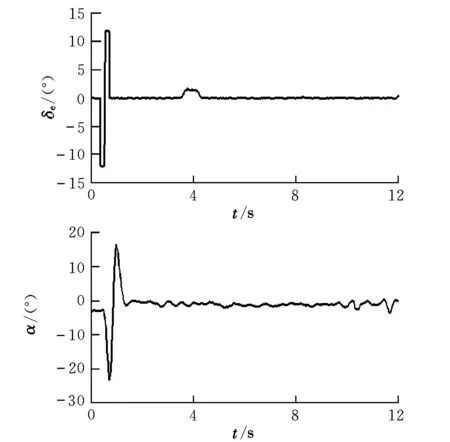
图2 升降舵激励信号及迎角响应估算曲线Fig.2 Elevator input and response of angle of attack
3.2 逐步回归法的基本原理
纵向参数辨识采用逐步回归法,其基本思想是:将变量逐个引入,引入变量的条件是其偏回归平方和经检验是显著的;同时每引入一个新变量,对已选入的变量要进行逐个检验,将不显著变量剔除。这样保证最后所得的变量子集中的所有变量都是显著的,经若干步可得“最优”变量子集[8]。具体思想如下:
设有m个自变量xj(j=1,2,…,m),因变量为y,有n个观测点。根据最小二乘原理,y的估计值为:
(5)
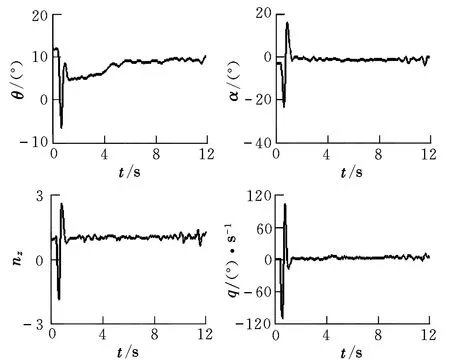
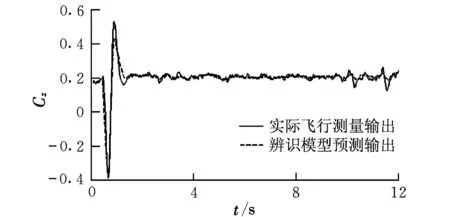
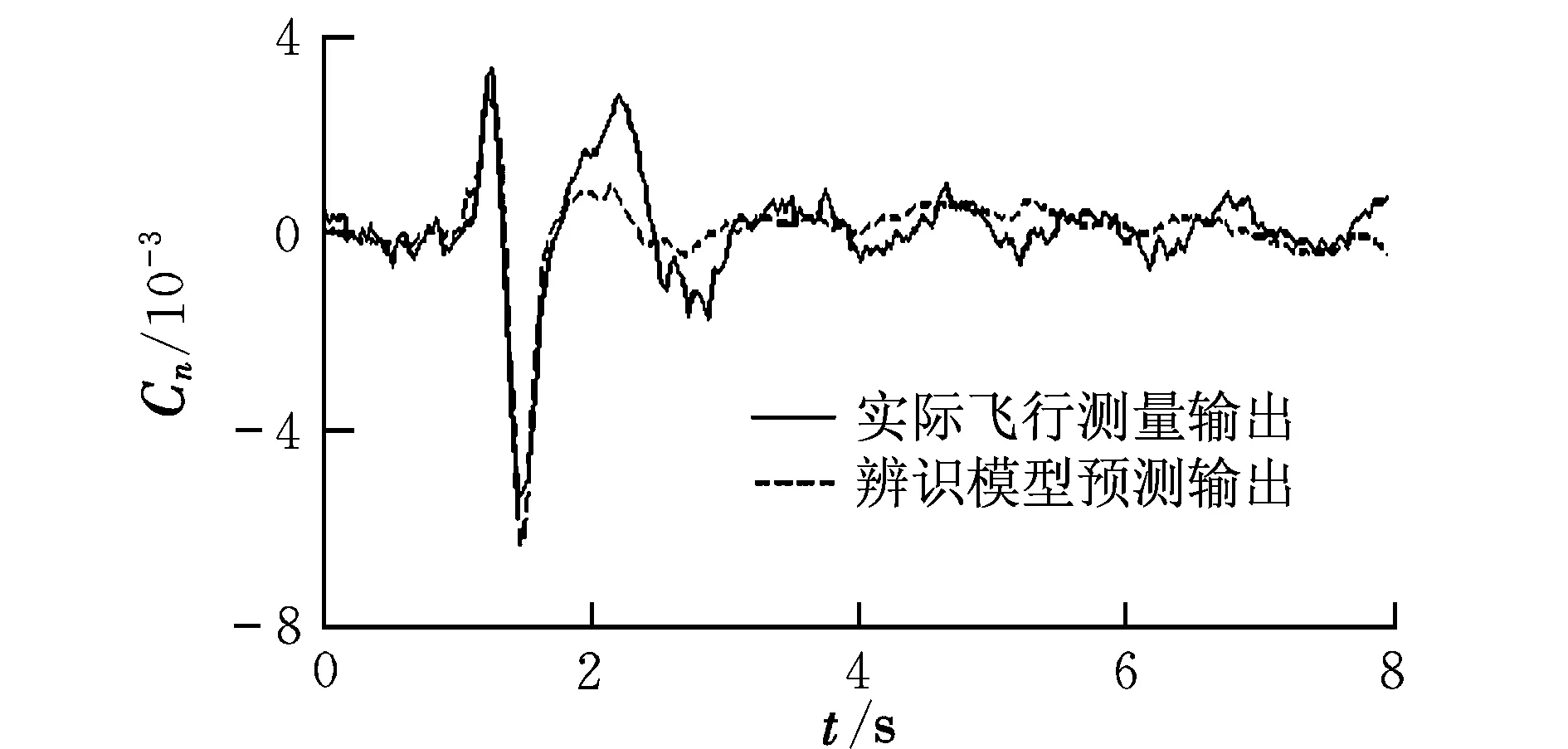
式中,l 推力T沿体轴系xB轴,此处xB轴向后,zB轴向上。飞机的纵向力平衡方程[9]为: (6) (7) 利用飞行试验数据,可得到相应的气动系数值用于参数辨识。Cz的回归方程可写为[10]: Cz=CzαΔα+CzqΔq+CzδeΔδe+Czα2Δα2+Cz0 (8) 待辨识参数有Czα,Czq,Czδe,Czα2,Cz0。 在图2所示激励下的部分状态量动态响应曲线如图3所示。 图3 无人机的纵向动态响应Fig.3 Longitudinal dynamic response of UAV 采用逐步回归法,对Cz的各项导数进行参数辨识,得到表2所示的辨识结果。 利用辨识所得参数计算得到Cz的辨识模型预测输出,与其试验曲线的对照如图4所示。 图4 垂向力系数辨识模型预测值与试验值对比Fig.4 Identification result and flight test result of vertical force coefficient 可以看出,Cz的辨识模型预测输出与其实际测量计算曲线能够很好地吻合。经计算,二者拟合误差为10.31%,辨识精度较为满意。由于辨识过程是在无风假设基础上进行的,大气扰动可能会对辨识精度带来一定误差。 将辨识得到的各项导数值代入式(8)可得到各状态量的辨识模型预测输出。与飞行试验测量曲线进行对照,可以用来检验辨识所得气动参数的正确性。以俯仰角速度为例,其辨识模型预测输出和实际飞行测量输出对比如图5所示。 图5 俯仰角速度的辨识模型预测值与试验值对比Fig.5 Identification result and flight test result of pitch rate 可以看出二者能够很好地吻合。经检验,其他相关状态量辨识曲线与试验测量曲线均能较好地吻合,说明以上辨识结果是可信的。 在飞机横侧向气动参数辨识试验中,对副翼进行偶极方波激励,取右副翼下偏为正偏角。 同上文所述,可得到侧滑角的估算值。图6为副翼偶极方波激励及其对应的侧滑角响应曲线估算结果。 图6 副翼激励信号及侧滑角响应估算曲线Fig.6 Aileron input and response of side slip angle 横侧向参数辨识采用最小二乘法。在系统辨识领域中,这是一种基本的估计方法。随机环境下使用最小二乘法时,并不要求观测数据提供其概率统计方面的信息,而其估计结果却有相当好的统计特性[11]。最小二乘估计算法的数学形式可以简要描述如下: (9) (10) (11) J为极小值的充分条件是: (12) 即矩阵ΦTΦ为正定矩阵,或者说矩阵ΦTΦ是非奇异的。 此处取欧美体轴系[6],由力矩平衡方程 (13) 可以得到基于飞行试验数据的力矩系数计算公式。其中以偏航力矩系数Cn为例: (14) 同理Cn的回归方程可写为[10]: Cn=CnβΔβ+CnpΔp+CnrΔr+CnδaΔδa+Cn0 (15) 待辨识参数有Cnβ,Cnp,Cnr,Cnδa,Cn0。 在图6所示激励下的部分状态量动态响应曲线如图7所示。 图7 无人机的横侧向动态响应Fig.7 Lateral dynamic response of UAV 用上述最小二乘法对Cn的气动导数和操纵导数进行参数辨识,其结果如表3所示。 表3 最小二乘法辨识结果Table 3 Least square method identification results 利用表3中的辨识结果,可以得到Cn的辨识预测输出,与实际试验值的对照如图8所示。 图8 偏航力矩系数辨识模型预测值与试验值对比Fig.8 Identification result and flight test result of yaw moment coefficient 从对比曲线可以看出,Cn的辨识曲线与其试验曲线吻合较好,计算可知二者拟合误差为14.36%。与前述Cz的辨识结果相比,Cn的辨识精度略低,其原因在于飞机横侧向运动比纵向复杂,存在横航向耦合。各状态量的测量误差和大气扰动都会对辨识精度产生一定的影响。 与纵向参数辨识结果检验方法类同,将所得Cn的导数值代入式(15),得到各相关状态量的辨识模型预测输出,与其实际飞行试验测量输出进行对照即可检验辨识结果的正确性。以偏航角速度r为例,其辨识模型预测输出和实际飞行测量值对比如图9所示。 图9 偏航角速率辨识模型预测值与试验值对比Fig.9 Identification result and flight test result of yaw rate 从图9可以看出,r的辨识模型预测输出与实际飞行测量输出能够很好地吻合。经验证,其他相关状态量辨识曲线与试验测量曲线均能较好地吻合,说明表3中的辨识结果是可信的。 逐步回归法与最小二乘法均适用于纵向和横侧向参数辨识,得到的结果较为接近,故本文不再赘述。 本文提出了根据试验可测数据估算迎角和侧滑角以及气动系数进而用于气动参数辨识的方法。该方法是在无人机试验条件有限、无法测得准确气动角的情况下完善飞行数据的一种简化方法。以某小型飞翼无人机飞行试验数据为例,验证了该方法用于无人机气动参数辨识的有效性,辨识结果满足一定精度要求。 考虑到辨识建模在数学本质上具有通用性,该方法不仅适用于本文研究的小型飞翼无人机,对其他布局形式的固定翼无人机的气动参数辨识也是普遍适用的。经检验,所得气动参数辨识结果具有正确性和工程实用性,可以进一步推广应用于无人机飞行仿真、飞行品质评价和控制系统设计等。 参考文献: [1] Younsaeng Lee,Seungjoo Kim,Jinyong Suk,et al.System identification of an unmanned aerial vehicle from automated fight tests[R].AIAA-2002-3493,2002. [2] 蔡金狮.飞行器系统辨识学[M].北京:国防工业出版社,2003:247-248. [3] Brad Seanor,Giampiero Campa,Yu Gu,et al.Formation flight test results for UAV research aircraft models[R].AIAA-2004-6251,2004. [4] Morelli E A.Identification of low oder equivalent system models from flight test data[R].NASA/TM-2000-210117,2000. [5] 中国人民解放军总装备部军事训练班教材编辑工作委员会.模型自由飞试验[M].北京:国防工业出版社,2002:181-182. [6] Etkin B.Dynamics of atmospheric flight[M].Newyork: John Wiley & Sons,Inc.,1972:108-110. [7] Jategaonkar R V. Flight vehicle system identification-a time domain methodology[M].USA:AIAA,2006:93-94. [8] 李言俊,张科.系统辨识理论及应用[M].北京:国防工业出版社,2006:51-63. [9] Vladislav Klein,Morelli E A.Aircraft system identification-theory and practice[M].USA:AIAA Education Series,2006:47. [10] Morelli E A.System identification programs for Aircraft[R].AIAA-2002-4704,2002. [11] Pinkelman J K,Batill S M,Kenoe M W.An investigation of the total least-squares criteria in time domain based,parameter identification for flight flutter testing[R].AIAA-1995-1247-CP,1995.3.3 辨识过程及结果

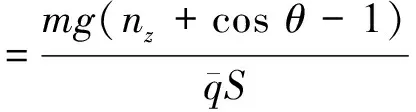

4 横侧向参数辨识
4.1 侧滑角计算结果
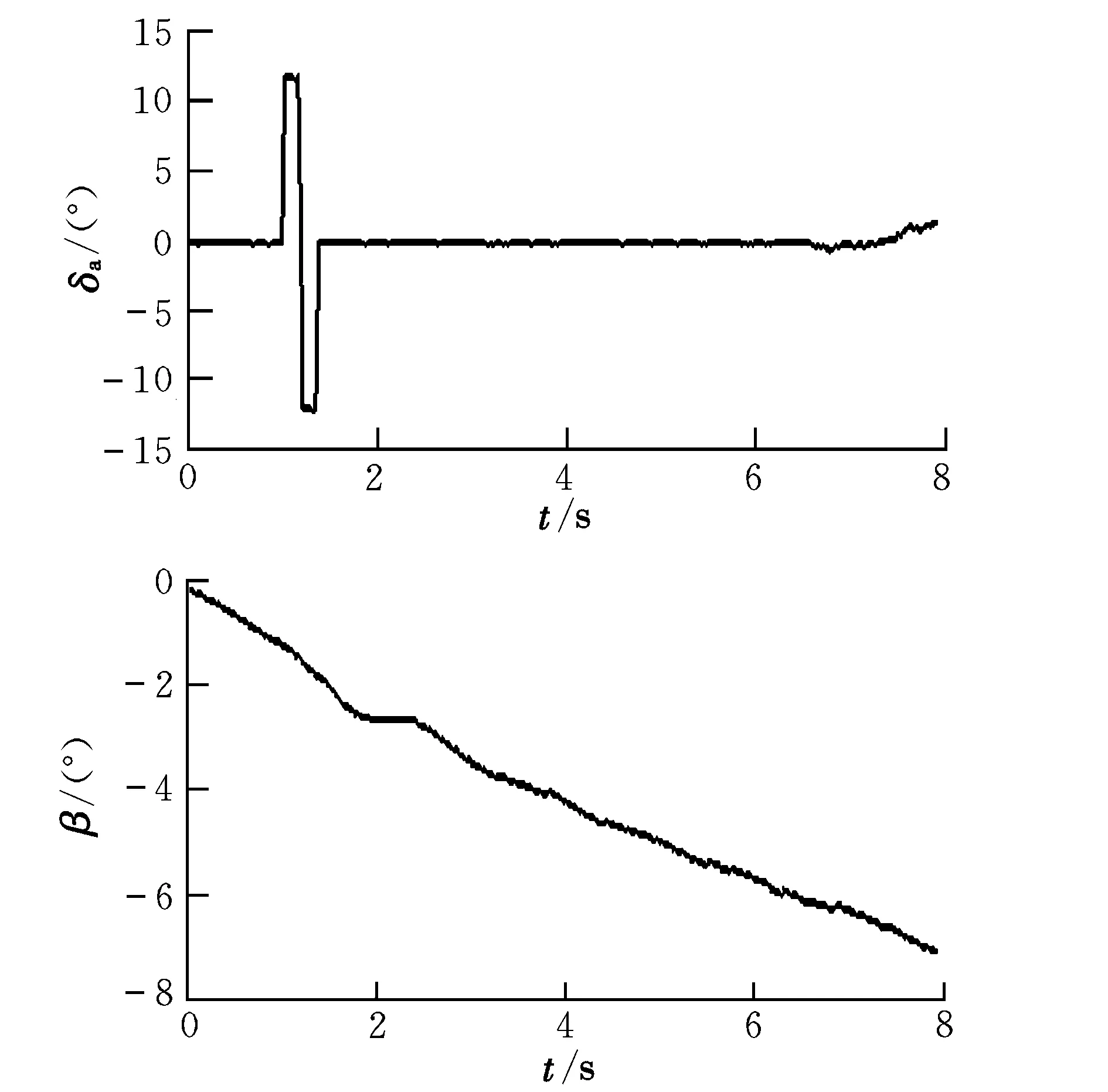
4.2 最小二乘法的基本原理
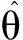
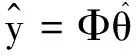
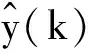
4.3 辨识过程及结果



5 结束语

