翼尖小翼对尾涡安全间隔的影响研究
魏志强, 刘菲, 刘薇
(1.中国民航大学 空中交通管理学院, 天津 300300;2.天津市空管运行规划与安全技术重点实验室, 天津 300300)
0 引言
飞机在飞行中形成的尾涡会在重力、大气湍流、风速、粘性等作用下,形成强度逐渐衰弱的尾涡流场。当后机进入前机所形成的尾涡流场时,在诱导下洗速度作用下,可能会发生倾斜、滚转、失速、急剧俯仰等影响飞行安全的危险情况。现行的尾涡安全间隔标准在尽可能避免此类危险的同时也在一定程度上限制了机场和终端区的容量[1]。
在尾涡形成及强度消散的建模研究方面,文献[1]建立了尾涡流场的快速仿真计算模型;文献[2]建立了三阶段尾涡消散模型,并与采用大涡模拟方法(LES)的数值计算结果进行了对比分析;基于LES方法的数值计算结果,文献[3]对快速仿真计算模型进行了精度评估分析;文献[4]研究了地面效应对尾涡模型的影响问题;周彬等[5]研究建立了飞机尾涡快速建模方法,所得结果详细描述了尾涡系统中保守被动量在不同时刻的状态分布特性;魏志强[6]对尾涡流场的仿真建模技术以及尾涡安全间隔仿真计算平台进行了编程开发;韩红蓉等[7]研究了飞机遭遇尾涡后的响应与安全间隔计算模型。
虽然国内外研究者在尾涡流场及安全间隔的建模方面开展了大量研究,但这些研究尚没有考虑飞机翼尖小翼的影响。为降低飞机的气动阻力、减少飞行油耗、提高运行经济性,航空公司在飞机厂家支持下对B737-800等飞机进行了融合式翼尖小翼改装[8]。由于降低了翼尖涡强度,使得加装翼尖小翼后的飞机尾涡初始强度、尾涡安全间隔也会有所降低。因此有必要基于对加装翼尖小翼后飞机诱导阻力的变化研究来分析其对尾涡安全间隔的影响。本文通过对飞机极曲线的拟合研究,分析了加装翼尖小翼后飞机诱导阻力的变化情况,提出用当量展弦比来表示翼尖小翼对尾涡涡强度的影响。然后以B737-800和B737-800W飞机的气动原始数据为例来对比分析翼尖小翼对尾涡初始强度、尾涡诱导力矩系数的影响,最后在尾涡安全间隔仿真计算平台上对加装翼尖小翼后的尾涡安全间隔进行了计算对比和分析。
1 翼尖小翼的气动效应分析
飞机的气动阻力从形成原因上可分为废阻力和诱导阻力两部分,其中诱导阻力的大小主要取决于翼尖涡的强度。加装翼尖小翼后,可以降低翼尖涡的强度,从而使飞机的诱导阻力降低,提高了飞机的气动性能。因此,可以通过对比加装翼尖小翼后飞机诱导阻力的变化情况来研究逆向翼尖涡的强度变化以及对尾涡安全间隔的影响。本文以B737-800和加装了翼尖小翼后的B737-800W飞机气动原始数据为例,来对比分析翼尖小翼对飞机气动参数的影响。
1.1 翼尖小翼对飞机气动阻力的影响
民航飞机的起降阶段属于低速飞行范畴,表1为B737-800飞机和B737-800W飞机的低速极曲线数据。从表中的数据对比可以看出,在相同升力系数下,加装翼尖小翼后的飞机在起降阶段的阻力系数减小量在3%左右,因此在其他条件一定时,起降阶段飞机的气动阻力会降低3%左右。
1.2 B737-800飞机气动特性的拟合分析
根据民航飞机的基本空气动力特性,飞机阻力系数的成分及影响因素可通过下式来表示:
CD=CD0+(CL2/πλ)δ
(1)
式中,CD0为废阻力系数;λ为B737-800飞机的展弦比,取9.45135;δ为飞机机翼平面形状系数。基于表1中CL和B737-800飞机的CD数据,对式(1)中的CD0和δ进行拟合,可得:
(2)
式中,xi=CLi2/πλ;yi=CDi;n为表1中极曲线数据的列数。将数据代入式(2)后可以得到CD0=0.018;δ=1.32345。
图1为拟合计算结果与原始数据的对比分析。可以看出,在飞机起降阶段的拟合精度一般不超过1%,满足后续研究的需要。
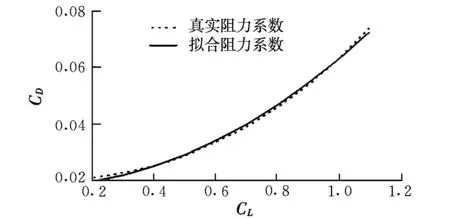
图1 真实阻力系数与拟合阻力系数的对比关系Fig.1 Comparison of real drag coefficient and fitting drag coefficient
1.3 B737-800W飞机气动特性的拟合分析
B737-800W飞机是在B737-800基础上加装了翼尖小翼。其对飞机翼尖涡强度的影响可以假定机翼平面形状系数不变,而展弦比发生变化,即需要根据B737-800W的低速极曲线数据(见表1)拟合出当量展弦比(λE)。根据式(1),经过二次曲线拟合后得到的当量展弦比为:
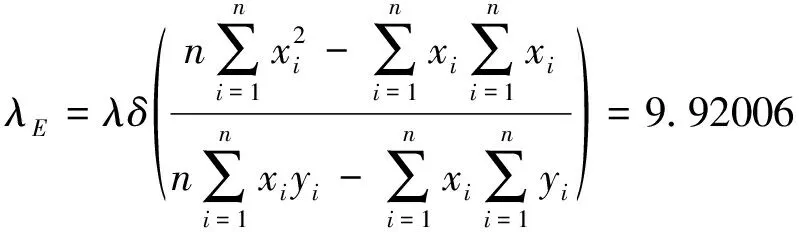
(3)
在式(3)中,xi和yi的表达式同式(2),但其中的升力系数和阻力系数取B737-800W飞机的气动数据。通过式(3)中当量展弦比和B737-800W真实展弦比(与B737-800相同,即9.45135)数据的对比,可以得到加装翼尖小翼后,对翼尖涡强度的影响相当于展弦比增加了4.96%。
2 翼尖小翼对尾涡安全间隔的影响
飞机加装翼尖小翼后对尾涡初始强度、强度消散和尾涡安全间隔影响可以通过当量展弦比的变化来分析。
2.1 翼尖小翼对尾涡初始强度的影响
根据亥姆霍兹涡定理,涡线不可能在流体内终止[1]。因此,当附着涡系的强度改变时,就会有同样环量改变的涡线离开附着涡而向下游拖出去,形成翼尖涡。在飞行中,飞机的升力又可以表示为飞机质量与过载系数之积。即:
L=ρVΓ0bπ/4=nymg
(4)
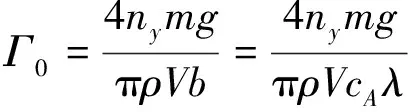
(5)
式中,Γ0为尾涡的初始强度,即尾涡环量;ρ为大气密度;V为飞机真空速;b为翼展;cA为几何平均弦长;m为飞机质量;ny为飞机法向过载。因此,展弦比的增加会导致尾涡初始强度的减少,具体影响如下式所示:
%=95.27%
(6)
式中,Γ为B737-800飞机的初始环量;ΓW为B737-800W飞机的初始环量。可以看出,在其他条件一定的情况下,加装翼尖小翼后的初始环量会降低4.73%。
2.2 翼尖小翼对尾涡强度消散的影响
飞机翼尖涡流场形成后的强度消散可以分为两个阶段。近场涡的范围从飞机机翼之后开始沿飞行反方向持续到大约6个翼展的距离,也叫尾涡的卷起区(起动区),强度基本不变;在远场涡阶段,强度快速消散。
利用已有的尾涡安全间隔仿真计算平台[6],对B737-800飞机和B737-800W飞机的尾涡消散情况分别进行了计算对比,其中B737-800W按当量展弦比来进行计算,以考虑翼尖小翼的影响,飞机质量为70000 kg,飞行高度600 m,速度80 m/s,涡消散率0.04,标准大气环境(ISA)。计算结果如图2所示。可以看出,在近涡消散阶段,加装翼尖小翼后尾涡的强度会有所降低,而在远涡阶段则基本没有影响。

图2 翼尖小翼对尾涡消散的影响Fig.2 Influence of winglets on vortex decaying
2.3 翼尖小翼对后机上诱导力矩的影响
后机进入前机所形成尾涡流场后,在诱导下洗和上洗气流的作用下,机翼上升力会发生变化[5]:
(7)

≈CαLVZ(y)/V
(8)

(9)
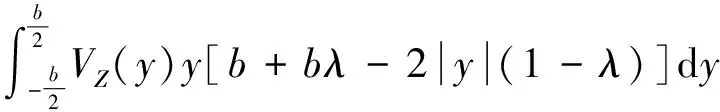
(10)
由于B737-800W飞机的当量展弦比大于B737-800,因此导致初始强度、后机上诱导滚转力矩系数会有所降低。本文以B737-300为后机进行计算分析,其中后机质量54000 kg,高度与前机相同,位置在前机之后4500 m,其他参数同2.2节。计算结果表明,加装翼尖小翼的B737-800W与B737-800相比,由于尾涡初始强度的降低,使得相同气象条件下对后机的诱导力矩系数降低了约6%~8%,具体如表2所示。

表2 前机加装翼尖小翼对后机上诱导力矩系数的影响Table 2 Influence of the front aircraft with winglets on induced moment coefficient of the following aircraft
2.4 翼尖小翼对尾涡安全间隔的影响
利用已有的尾涡安全间隔仿真计算平台,以B737-300飞机为后机,计算分析了前机加装翼尖小翼后对前后机之间尾涡安全间隔的影响,计算条件同2.3节。
结果表明,由于前机尾涡初始强度的降低,使得相同气象条件下的尾涡安全间隔会减小3.5%左右,具体如表3所示。

表3 翼尖小翼对尾涡安全间隔的影响Table 3 Influence of winglets on wake vortex safety spacing
3 结束语
国内外学者在尾涡建模方面开展了大量研究,但尚未考虑飞机翼尖小翼的影响。本文通过对飞机极曲线的拟合研究,提出用当量展弦比来表示翼尖小翼对尾涡涡强度的影响,进而计算分析了翼尖小翼对尾涡初始强度、诱导力矩系数和尾涡安全间隔的影响。相关研究可为更准确地计算尾涡流场影响区域和尾涡遭遇安全分析提供必要的理论依据。本文通过对气动数据拟合分析来类比翼尖小翼对尾涡的影响,更进一步的研究则可通过数值模拟或风洞试验的方法来更精确地计算分析翼尖小翼的影响。
参考文献:
[1] 魏志强,徐肖豪.飞机尾涡流场的建模与仿真计算研究[J].交通运输系统工程与信息, 2010,10(4):186-191.
[2] Proctor F H,Ahmad N N,Switzer G S.Three-phased wake vortex decay[R].NF1676L-10242,2010.
[3] Proctor F H,Hamilton D W.Evaluation of fast-time wake vortex prediction models[R].AIAA-2009-0344,2009.
[4] Sereno J L,Pereira J C F.Uncertainty quantification of two-dimensional wake vortices near the ground[J].Journal of Aircraft,2012,49(4):1175-1178.
[5] 周彬,王雪松,王国玉.飞机尾涡的快速建模方法[J].航空动力学报,2009,24(1):110-115.
[6] 魏志强. 动态尾涡安全间隔计算工具的开发与实现[J].航空计算技术, 2010,40(5):87-90.
[7] 韩红蓉,李娜,魏志强.飞机遭遇尾涡的安全性分析[J].交通运输工程学报,2012,12(1):45-49.
[8] Panagakos A,Lee T.Effect of wing let dihedral on a tip vortex[J].Journal of Aircraft, 2006,43(1):117-124.

