四阶行列式对角线法则的图解法

刘希强， 赵 颖， 王 璞， 毛 磊

(解放军理工大学理学院数学系，江苏南京211101)

1 引 言

在通常的《线性代数》或《高等代数》教材[1,2]中涉及到行列式的内容时，都会首先介绍二阶和三阶行列式的对角线法则，然后找出一般性的规律，从而给出n阶行列式的定义，广大师生也只能较好地掌握一些特殊行列式的计算，对于一般的四阶或者高阶行列式的展开缺少行之有效的方法.本文利用图解法，推导出四阶行列式的对角线法则，扩展了对角线法则的应用范围，使四阶行列式的计算更具有可操作性.

2 二阶和三阶行列式对角线法则的图解法

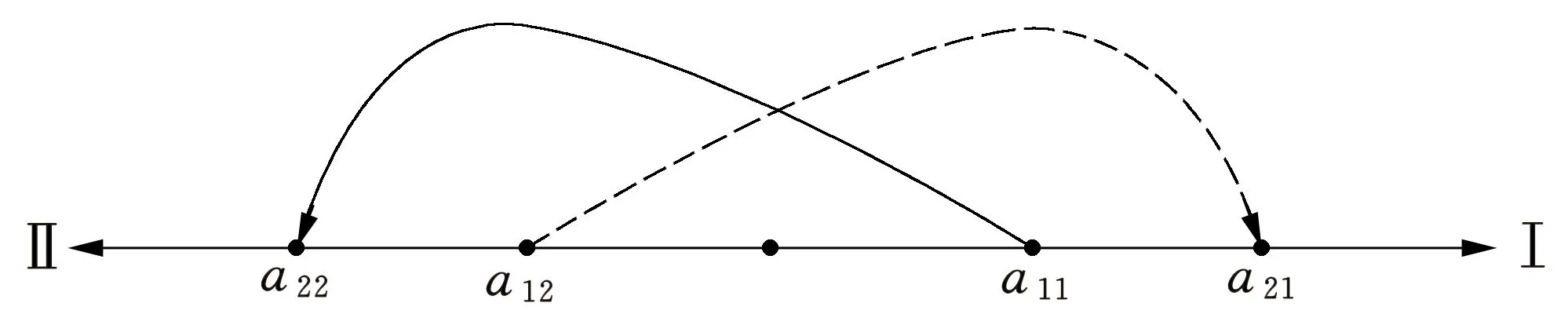
图1 二阶行列式图解法

即a21，这两个元素构成了行列式展开的第二项a12a21，只是它被冠以负号.这两项合在一起，就得到二阶行列式的值.

三阶行列式按照对角线法则展开，可以得到

图2 三阶行列式对角线法则的图解法

可按图2所示方法记忆.射线Ⅰ，Ⅱ，Ⅲ按逆时针方向排列，将行列式的三列元素仿照图1的规则依次标记在射线Ⅰ，Ⅱ，Ⅲ上.在射线Ⅰ上从第一个元素a11开始取，按照逆时针方向，第二个取射线Ⅱ上行标为2的元素a22，第三个取射线Ⅲ上行标为3的元素a33，这三个元素的乘积构成三阶行列式的第一项.若按照顺时针方向，第二个取射线Ⅲ上行标为2的元素a23，第三个取射线Ⅱ上行标为3的元素a32，这三个元素的乘积构成三阶行列式的第二项，并冠以负号.其余各项可按照类似的方法得到.可以发现，逆时针方向取正号，顺时针方向取负号.

3 四阶行列式的对角线法则

四阶行列式

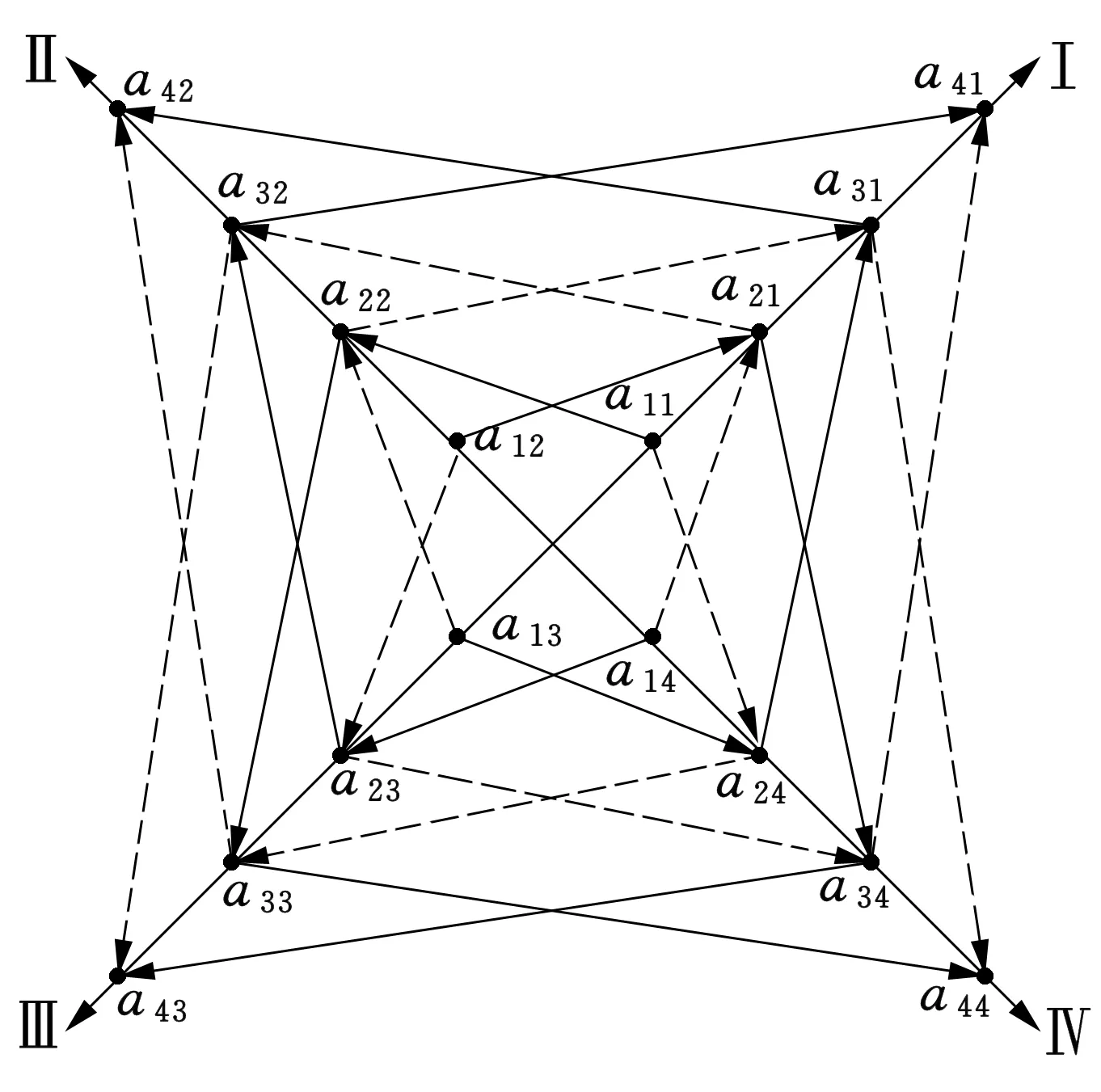
(a) ⅠⅡ Ⅲ Ⅳ上为第1234列的元素

=a11a22a33a44-a11a24a33a42+a12a21a34a43-a12a23a34a41

+a13a24a31a42-a13a22a31a44+a14a23a32a41-a14a21a32a43

+a11a23a34a42-a11a22a34a43+a13a21a32a44-a13a24a32a41

+a14a22a31a43-a14a23a31a42+a12a24a33a41-a12a21a33a44

+a11a24a32a43-a11a23a32a44+a14a21a33a42-a14a22a33a41

+a12a23a31a44-a12a24a31a43+a13a22a34a41-a13a21a34a42，

(b) Ⅰ Ⅱ Ⅲ Ⅳ上为第1342列的元素 (c) ⅠⅡ Ⅲ Ⅳ上为第1423列的元素图3 四阶行列式对角线法则的图解法

可按图3中的三个图进行记忆.射线Ⅰ上标记第一列的元素，在(a),(b),(c)中，射线Ⅱ，Ⅲ，Ⅳ上依次标记第234，342，423列的元素.射线Ⅰ，Ⅲ上逆时针方向取正号，顺时针方向取负号，射线Ⅱ，Ⅳ上顺时针方向取正号，逆时针方向取负号.最后，不同射线上不同行标元素乘积的代数和即为四阶行列式的展开式.

4 结 论

行列式的对角线法则不仅仅适用于二阶和三阶行列式，四阶行列式也可以用对角线法则来计算，具体地可以利用图解法来描述，但是它们的规律各不相同，这些规律与行列式的定义是一致的，其乘积项中各元素的逆时针或顺时针方向是与元素下标排列逆序数的奇偶性相对应的.n阶行列式的对角线法则是值得进一步探讨的问题，这将使得一般的n阶行列式的计算更具有可操作性，有一定的意义.

[参 考 文 献]

[1] 同济大学数学系.工程数学线性代数[M].5版. 北京:高等教育出版社,2009.

[2] 北京大学数学系几何与代数教研室代数小组.高等代数[M].2版. 北京:高等教育出版社,2000.