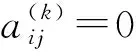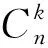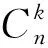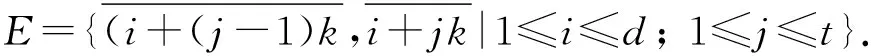循环逆M-矩阵的判定
林玉蕊, 陈绩馨
(福建农林大学计算机信息学院,福州350002)
1 引 言
逆M-矩阵是指其逆为M-矩阵的一类非负矩阵.这类矩阵有广泛的应用价值,受到国内外学者的很大关注.由于判定一般非负矩阵是否为逆M-矩阵非常困难,人们就着手研究一些特殊形式的非负矩阵[1-7].本文给出一个判定循环逆M-矩阵的简便方法.
2 预备知识
定义2.1设A=(aij)∈n×n满足aij≥0 (i,j=1,2,…,n),则称A为非负矩阵,记为A≥0.
定义2.2设A=(aij)∈n×n.若aij≤0 (i≠j;i,j=1,2,…,n),则称A为Z-矩阵,记为A∈Zn×n.
定义2.3设A∈n×n,A=sI-B,实数s>0且B≥0.如果ρ(B) 定义2.4若A≥0,且A-1存在,A-1∈Zn×n,则称A是逆M-矩阵. 定义2.5设A=(aij)∈n×n,B=(bij)∈n×n,如果aij=0当且仅当bij=0(1≤i,j≤n),则称A与B有相同的零位模式. 定义2.6形如 的矩阵C称为循环矩阵,记作C=Circ[c0,c1,…,cn-1]. 设〈n〉={1,2,…,n},有向图G=(N,E)由N个顶点1,2,…,n构成的顶点集N及有向边集E={(i,j)|i,j∈N}构成. 有向图G=(N,E)的路径是一个顶点序列v1,v2,…,vk,vk+1,vi∈N且(vi,vi+1)∈E,i=1,2,…,k,除了可能v1=vk+1外,其余的顶点均不相同.如果在路径中v1=vk+1,则称该路径为一个圈,记为{v1,v2,…,vk+1(=v1)},它的长度为k.如果对G=(N,E)的任意两个顶点vi,vj,在G中存在一条从vi到vj的路径,则称该有向图G是连通的,否则称G是不连通的.易知,长度为n的圈是连通的. 一个有向图G=(VG,EG)的子图是有向图H=(VH,EH),其中VH⊆VG,EH⊆EG且当u,v∈VH时(u,v)∈EH. 矩阵A=(aij)∈n×n的有向图记为D(A)=(N,E),其中顶点集是N=〈n〉且边集是E={(i,j)|aij≠0}. 给一个矩阵的图的顶点重新标号就相应于对矩阵作一个置换相似变换.因为逆M-矩阵在置换相似下是闭的,我们可以给一个逆M-矩阵的有向图以所需的标记.我们知道:矩阵A是不可约的充分必要条件是D(A)的有向图D(A)是连通的或者D(A)包含一个连通的子图. 为了研究循环逆M-矩阵的性质,下面引入一个新的有向图和一些记号.设gcd(n,k)是两个正整数n,k的最大公约数,即设 (3.1) 定义3.1如果一个有向图的顶点集是〈n〉且它的边集是 根据定义,我们有 引理4.1[8]如果n阶实矩阵A是不可约的逆M-矩阵,则A是正矩阵. 注 如果A是逆M-矩阵,则A,A2,…,Ak,…有相同的零位模式,这时称A是幂不变的零位模式. 引理4.3[8]设n阶非负矩阵A=(aij)有全为正的主对角元,则存在非负对角矩阵D使得A+D是逆M-矩阵的充分必要条件是A2与A有相同的零位模式. 引理4.4[9]设A是一个分块逆M-矩阵: 且Aii(i=1,2,…,r)是正主阵.如果Aij≠O,i≠j, 则Aij>0. (4.1) 引理4.6[10-12]如果A=Circ[c0,c1,…,cn-1]≠c0I是一个逆M-矩阵且存在一个正整数k使得ck>0,d=gcd(k,n)=1,则A是正的. 引理4.7设A是n×n循环矩阵Circ[c0,c1,…,cn-1]且n不是一个素数,则存在一个正整数k(k≥2),使得A置换相似一个带有循环块矩阵的块Toeplitz阵 (4.2) 这里所有的Bi都是循环矩阵, (4.3) 这里s=n-d+j.此外,若A是一个逆M-矩阵,k是使得ck≠0的最小整数,则B0是一个正逆M-矩阵. 由引理4.2易得下面推论: 推论4.1设A=Circ[c0,c1,…,cn-1]是逆M-矩阵,n有真因子n=pq(p≥2,q≥2),则循环矩阵 Circ[c0,cp,…,c(q-1)p], Circ[c0,cq,…,c(p-1)q] 是逆M-矩阵. 下面给出本文最主要的结果: 定理4.1设A=Circ[c0,c1,…,cn-1]≥0,A非正且A≠c0I.若存在一个正整数k,k是n的真因子,使得 (4.4) 且循环矩阵 C=Circ[c0,c1,…,c(t-1)k] (4.5) 是正逆M-矩阵,则A是逆M-矩阵. 证由假设条件,显然n不是一个素数,所以由引理4.2,A置换相似于(4.2)的块Toeplite矩阵B,其中每块是(4.3)中的循环矩阵.由条件(4.4)成立,则(4.2)中的B是对角矩阵diag(B0,B0,…,B0).因为A置换相似于B,而B0是逆M-矩阵,所以A是一个逆M-矩阵. 该结论表明:只有当正的C的下标是一个算术序列时,非负循环矩阵A=Circ[c0,c1,…,cn-1]≠c0I才有可能是一个逆M-矩阵.它可方便地判断一个非负但非正的循环矩阵是逆M-矩阵. [参 考 文 献] [1] Johnmn J C R. InverseM-Matrix[J]. Linear Algebra Appl, 1982, 47:195-216. [2] Xiang shuhuang, You Zaoyong. InverseM-Matrix problems[J]. Acta Mathematica Applicatae Siniea, 2001, 17(1): 14-19. [3] Johnson C R. InverseM-Matrices[J]. Linear Algebra and Its Application, 1982, 47: 195-216. [4] Lewin M. On inverseM-Matrix[J]. Linear Algebra and Its Application, 1989, 118: 83-94. [5] Willoughby R A. The inverseM-Matrix problem[J]. Linear Algebra and Its Application, 1977, 18: 75-94. [6] Markham T L. Nonnegative matrices whose inverses areM-Matrices[J]. Proc. Amer. Math. Soc, 1972, 36:326-330. [7] Soto R L. A sufficient condition for the existence of anM-Matrix with prescribed spectrum[J]. Comprters and Mathematics with Applications, 2001, 42: 849-859. [8] Yang C S and Xu C X. Propertise of Hadamard product of inverseM-Matrices[J]. Numerical Linear Algebra with Applications, 2004, 11: 343-354. [9] Berman A and Plemmons R J. Nonnegative matrices in the mathematical sciences[M]. SIAM Press, PL, 1994. [10] 张某成,黎稳.非负矩阵论[M].广州:广东高等教育出版社,1995. [11] 林玉蕊.分块逆M-矩阵的一个性质[J].福建农林大学学报(自然科学版),2006,35(1):109-110. [12] 陈景良,陈向晖.特殊矩阵[M].北京:清华大学出版社,2001.3 矩阵与图
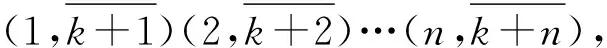

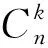

4 循环逆M-矩阵的判定