双中继无线电能传输系统建模及传输效率分析
王 维 黄学良 周亚龙 曹伟杰 谭林林
(东南大学电气工程学院 南京 210096)
1 引言
近几年来,随着无线电能传输技术研究的不断升温及其相关应用领域的不断拓宽,越来越多的研究学者对此项技术给予了足够的肯定。便携式小型家用电器的无线充电、植入式人体医疗设备的无线供电、电动汽车的无线充电等诸多领域竟相追逐,并在技术应用上取得了一定的突破[1,2]。相比之下,传统的电缆输电系统呈现出越来越多的弊端,在深海、煤矿、化工等特殊领域,存在火花、输电线路的铺设及维修困难等一系列安全性、建设性的问题,这使得这些行业迫切需要无线电能传输技术的支持。
在特斯拉打开了无线输电的思路之后,很长一段时间内,国内外学者对此技术都不感兴趣。自2007年 MIT在电磁共振原理上进行突破,并成功在2m以外点亮了一只60W的灯泡,才逐渐打破了电磁感应原理对以往多数科学家的束缚,为大功率、中距离无线电能传输技术的发展提供了一个新思路[3,4]。磁耦合谐振式无线电能传输技术是继激光、微波、电磁感应等传输方式后的一种新的传输方式。用于谐振耦合的能量收发线圈,通过电容补偿,使得线圈自身谐振频率保持一致,由此可进行电能的高效、长距离、大功率的传输[5,6]。
本文针对双中继无线电能传输系统进行建模,并从能量投递层面,通过理论及仿真分析、实验验证的方式,对其中继层发射与接收天线间的能量传输效率进行分析,同时引入耦合系数的概念,探讨线圈耦合强弱与其传输效率的关系,并着重从能量接收线圈的匝数设计入手,分析在给定的无线电能传输共振系统下,接收线圈是否存在最优化匝数,使得系统能量传输效率达到最高,避免在实际系统设计中,对线圈匝数设计的盲目和不确定。
2 系统建模与互感分析
系统物理模型如图1所示,其包含励磁电源、励磁线圈、能量传输天线、能量接收天线、负载耦合线圈及负载组成。励磁电源为高频电压源,产生高频正弦信号。通过励磁线圈的电磁变换并与能量传输天线间的互感强耦合关系将高频电磁信号耦合至能量传输天线侧。同理,基于互感耦合的方式,高频信号经由能量传输天线、能量接收天线及负载耦合线圈逐级传递至负载端,为负载提供其所需的能量。为了最大化传输电能,减少在空间耦合时不必要的能量辐射、内耗等能量耗散,本文采用能量逐级电容串联补偿式电路,如图1所示,补偿电容Cs、Ct、Cr、Cl分别为励磁线圈 Dl、能量传输天线Tx、能量接收天线Rx、负载耦合线圈Ll的补偿电容。通过补偿后的电磁共振模式,能量即可被高效率传输。同时通电导线在高频下具有很强的趋肤效应,故系统采用空心铜管来绕制上述各类线圈。图2为系统物理模型的侧视图。
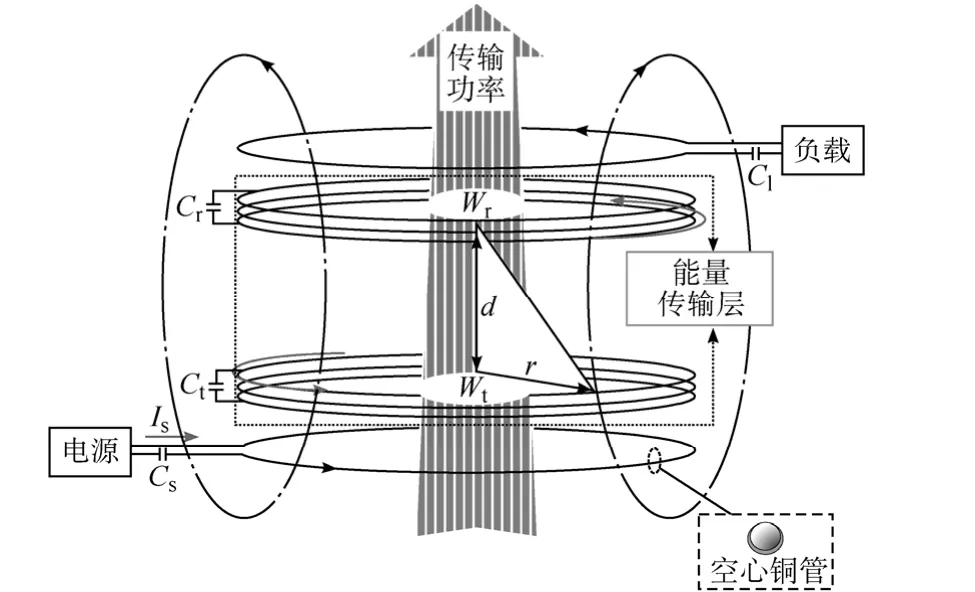
图1 系统物理模型图Fig.1 Physical model of system
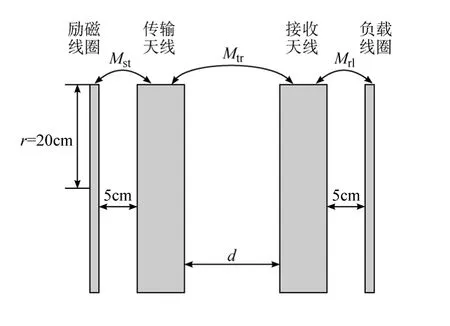
图2 系统物理模型侧视图Fig.2 The lateral view of physical model
电磁能量以磁共振模式在线圈间进行无线传输,线圈间的互感系数是能量耦合传输的关键因素所在。本文通过理论与仿真相结合的方法对线圈间互感系数进行分析,进而得出较为精确的系统电路模型,在此基础上,通过研究能量传输线圈与能量接收线圈间的耦合系数,进一步讨论系统能量传输层的传输效率与耦合系数的关系,从而对能量接收线圈进行最优化匝数设计。
对于本文所建立的无线电能传输系统,励磁与负载耦合线圈均为单匝铜管,能量传输天线与能量接收天线以多匝铜管螺旋绕制而成。对于空心线圈,其电感近似计算表达式为[7]

式中,L为电感量(μH);μ0为真空磁导率(4π×10-7H/m);N为线圈匝数;S为螺旋线圈的截面积(m2);l为螺旋线圈轴向长度(m);k为长冈系数,取决于2r/l的比值;r为线圈半径(m)。
如图2所示,在本文所设计的系统中,线圈半径r均为0.2m,铜管截面直径为0.002 7m,螺旋线圈轴向长度l为
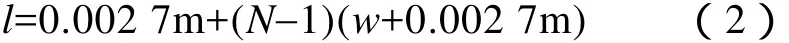
式中,w为两匝铜管间距,本文所设计系统中两匝铜管间距固定为w=0.005 5m。
表1中给出了由式(1)、式(2)及长冈系数k计算所得的电感理论值及由HIOKI公司的LCR测试仪的实测值,并对其进行了对比。
通过表1可看出,用式(1)、式(2)来描述本系统设计的螺旋线圈电感值较为精确。
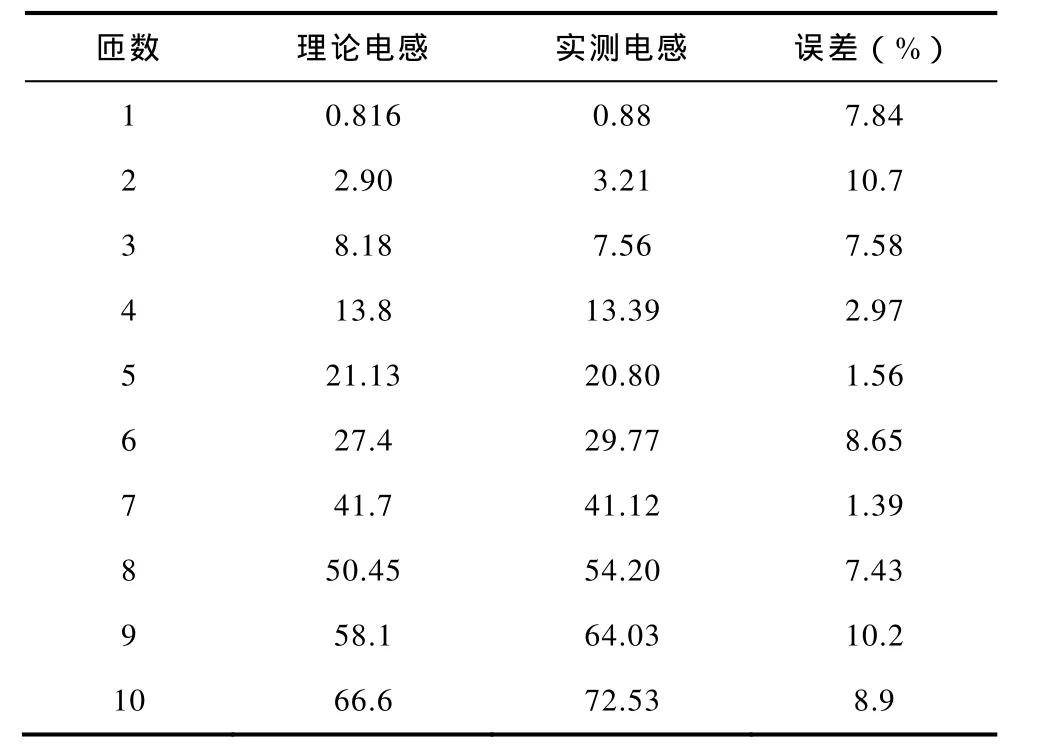
表1 不同匝数N下的空心螺旋线圈电感值Tab.1 Hollow spiral coil inductance value in different turns(单位:μH)
对于图2所示的无线电能传输系统,系统传输模型如图3所示,基于互感耦合机理,能量在线圈间传递主要依赖于励磁线圈与能量传输天线之间的互感Mst、能量传输天线与能量接收天线间的互感Mtr以及能量接收天线与负载耦合线圈间的互感Mrl。故本文采用理论与仿真相结合的方法对上述系统能量传递线圈间互感进行分析。
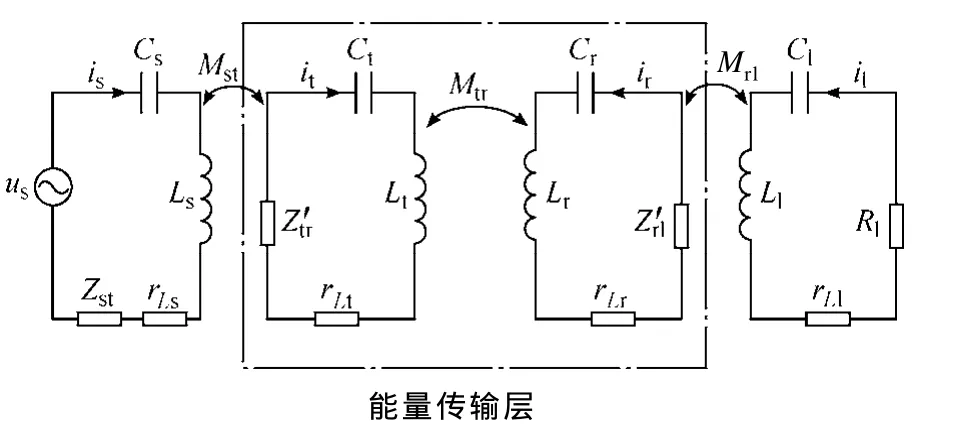
图3 磁耦合谐振式无线电能传输系统模型Fig.3 The model of magnetically coupled resonant wireless power transmission system
针对空间中两共轴平行线圈,其互感大小可由Neumann公式计算得出[8],即
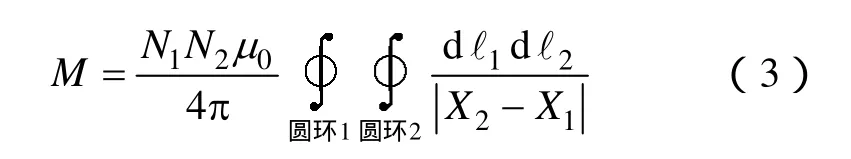
式中,μ0是磁常数;N1、N2为两线圈匝数;d ℓ1、 dℓ2为线圈1与线圈2上的微小线元素;X1为微小线元素dℓ1的坐标位置;X2为微小线元素dℓ2的坐标位置。
在图2所述各能量线圈中,线圈半径均为统一常量,即r=20cm;且励磁与负载耦合线圈均为单匝铜管,能量传输线圈为5匝,故线圈间互感可表示为
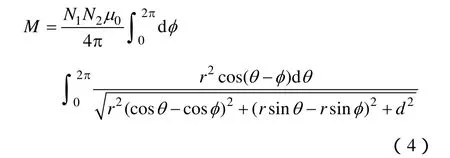
式中,θ、φ均为积分因子;d为两线圈间轴向距离。
通过Matlab仿真,令线圈1匝数为5,得出线圈1、2间互感随线圈匝数N、线圈轴向距离d的关系,如图4所示。
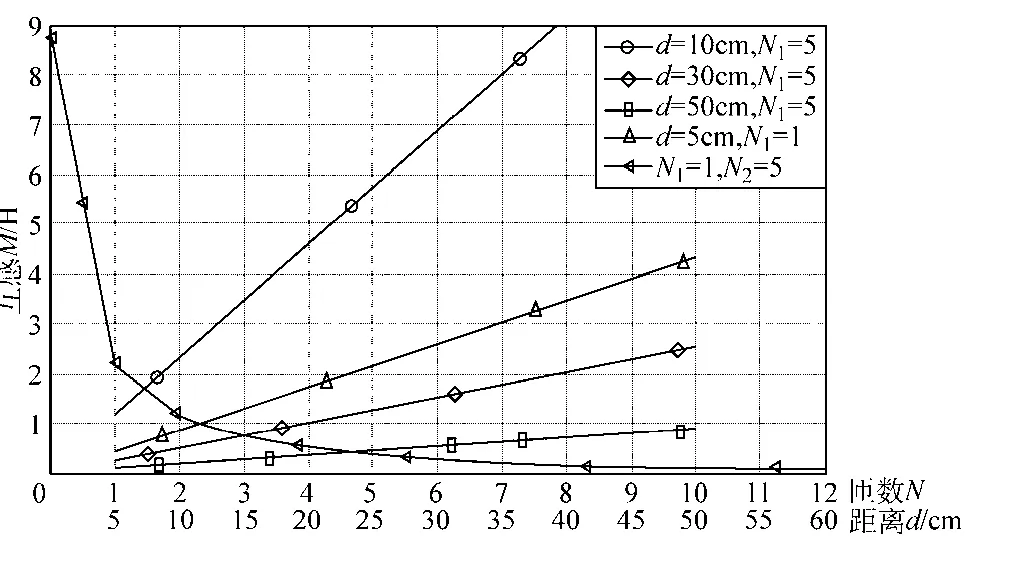
图4 互感随线圈匝数N或传输距离d变化图Fig.4 Mutual inductance varies with turns N of coils or transmission distance d
由图4可看出,当两线圈间轴向距离d及其中一个线圈匝数固定后(图中注视匝数为本文所设计系统中线圈采用的匝数),两线圈间互感值随另一线圈匝数呈线性变化,且匝数越多,互感值越大。当两线圈匝数均固定后,互感值随轴向距离d的增加几乎呈3次方衰减,故通过缩小两线圈间轴向距离或增加线圈匝数可显著提高线圈间的互感值。
3 系统传输效率分析
对于图3所示的无线电能传输系统互感耦合模型,本文着重从能量投递层面,分析能量传输层间系统传输效率与系统耦合系数之间的关系,并由此对给定系统其他参数条件下的接收线圈最优化匝数进行探究。
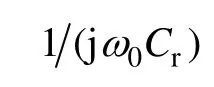
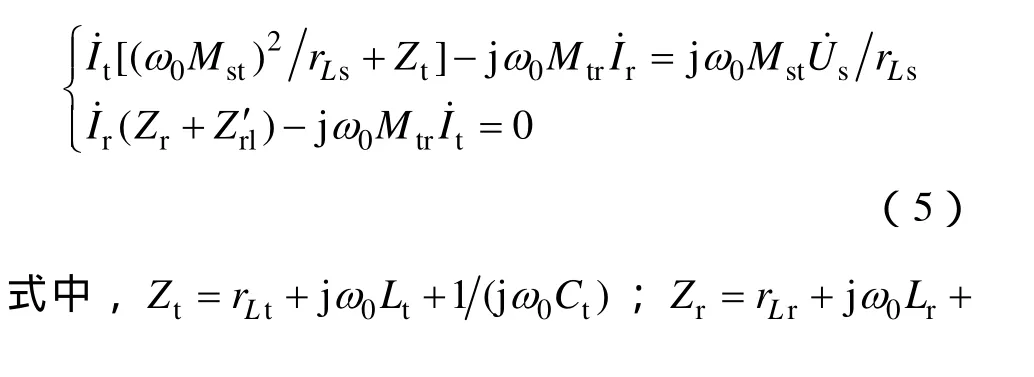
在本文效率分析时,考虑的是能量发射线圈与接收线圈之间的传输效率,因为负载回路可利用匹配电容使其保持谐振,故假设负载为确定的阻性负载,这不影响本文中线圈匝数对传输效率的分析。
由方程(5)可得
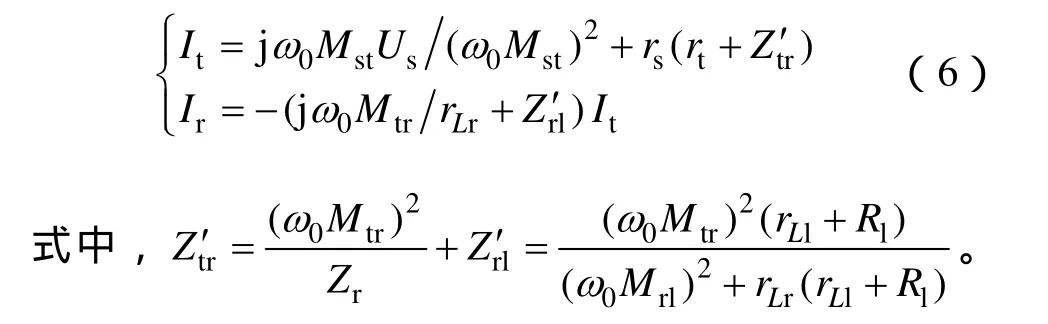
对于图3所示无线电能传输系统模型的能量传输层,能量传输在发射与接收天线之间,故能量传输层的传输效率与各线圈中储存的能量大小有密切关系,为了针对性研究线圈匝数与传输效率之间的关系,假定系统其余参数均为已知参数,能量接收线圈匝数Nr未知。式(7)给出了两线圈间传输效率及线圈中存储能量的基本表达式,即
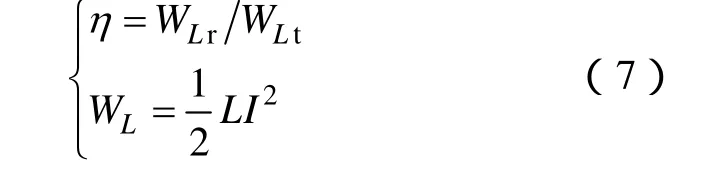
式中,WL表示线圈中存储的能量。
联立式(6)、式(7),可得能量发射、接收天线间的传输效率一般表达式为
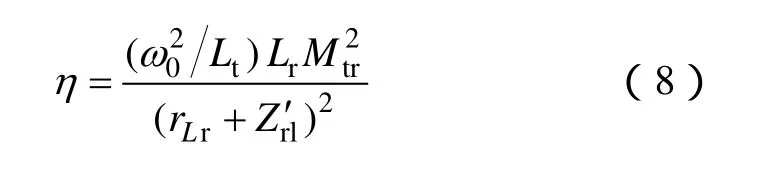
在式(8)中,因为各基本变量均为接收天线匝数Nr的函数,即
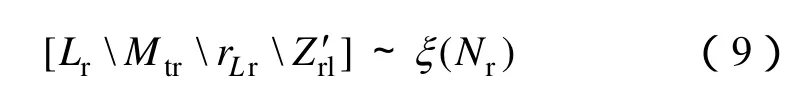
故能量传输层传输效率η亦为Nr的函数,即

对于线圈中的等效电阻rLr,由高频时线圈的损耗电阻rohm和辐射电阻rrad组成[9]。然而,辐射电阻rrad一般在10-4Ω数量级上, 所以相对于损耗电阻来说可忽略不计[10]。而螺旋线圈的损耗电阻可通过下式得出,即
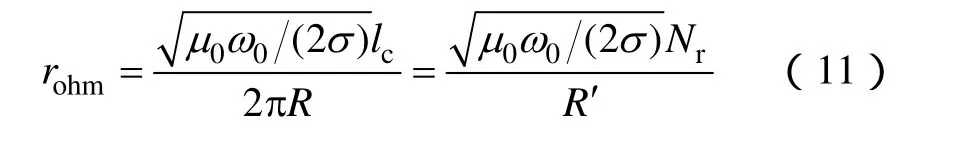
式中,N为线圈匝数;r为线圈半径(cm);R′为空心导线有效截面积半径(cm);σ为导体电导率(S/m)。
对于本文所述线圈,铜的电导率为 5.8×107S/m,R′=0.055cm。
结合上述各式,经化简可得能量传输层传输效率η与能量接收天线Nr的关系式为
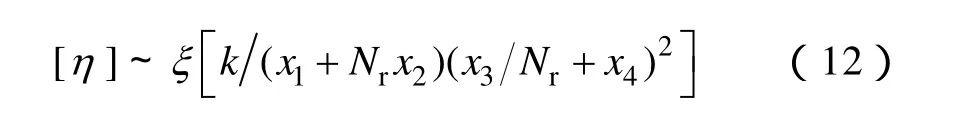
式中,x1、x2、x3、x4为包含r、R、R′、ω0、d、Rl等系统原始参数的组合定参数;k为随Nr增加的非线性增长系数。
由式(12)可以明显看出,η随Nr的增加并非为单调函数,对于任意如图1所述的无线电能传输系统,存在不止一个最优匝数Nr使得系统能量层传输效率达到局部最优值。而对于实际的系统,为使得系统始终处于共振状态,采用高频可调电容进行匹配。然而,一般情况下,匹配电容值是有限的,Nr与其匹配电容存在如下约束条件:
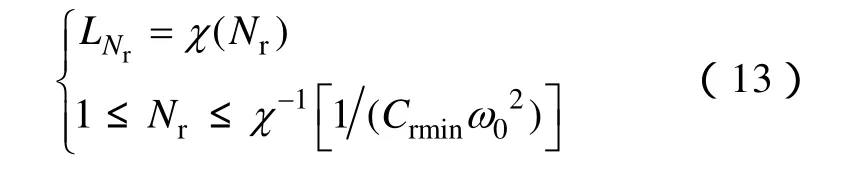
故综合考虑各项因素,传输效率η在有限接收线圈匝数下存在局部最优值。
为了更好的分析发射与接收线圈间耦合力与系统传输效率之间的关系,本文引入耦合系数k表示发射与接收线圈间的耦合关系[11],可由下式表示。

对于能量发射线圈及线圈间轴向距离d确定的无线电能传输共振系统,耦合系数k与接收线圈匝数存在如下式的关系,即
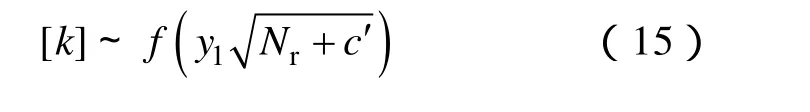
式中,c′为定常数;y1为不定常数,随着Nr的增加呈非线性衰减趋势。
由y1特性可知,耦合系数k随着Nr的增加,在某一区间内存在极大值,但随着Nr的继续增加,耦合系数则呈不断增长趋势,即通过增加线圈匝数可以增强两线圈间的耦合关系。同时,系统传输效率可表示为耦合系数k的函数关系,即
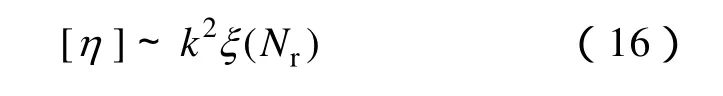
4 系统传输效率与耦合系数的仿真与实验分析
为了能够更加直观的描述系统能量传输效率与接收线圈设计之间的关系,本文采用Matlab软件对理论分析进行仿真研究,旨在验证理论分析的正确性,同时得出两者间的内在关系,并由此对接收线圈进行优化设计,以满足电能高效无线传输的要求。
同时,为了更好的验证本文所分析理论的正确性,本文对仿真结果进行了较为精确的实验验证,实验相关参数见表2,实验装置如图5所示。
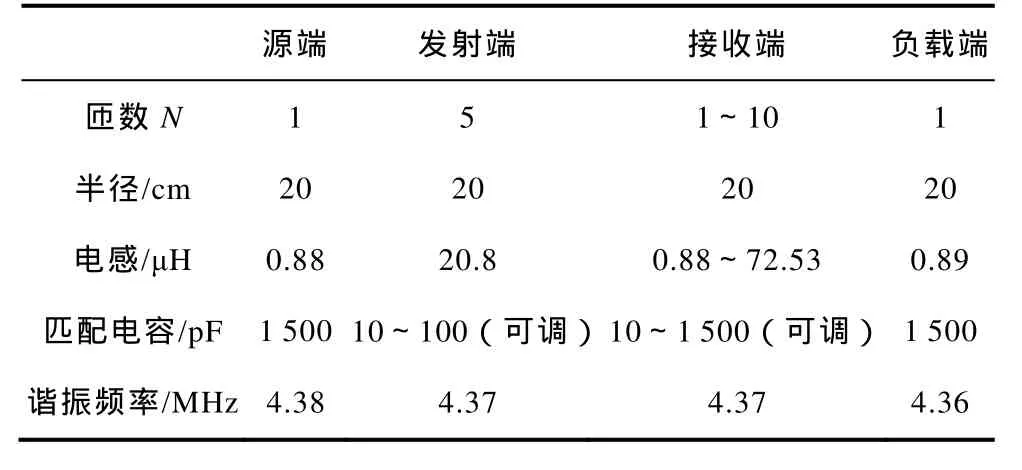
表2 磁耦合谐振式无线电能传输系统实验参数Tab.2 Experimental parameters of magnetically coupled resonant wireless power transmission system

图5 实验装置图Fig.5 The experiment device
当系统其余参数均确定时,效率、耦合系数分别可表示为与接收线圈匝数、传输距离之间的关系,如图6和图7所示。然而,系统传输效率与线圈内的损耗有着直接的关系,而随着线圈匝数的增加,能量发射与接收线圈间互感、自身电感、线圈内阻均随之增加,导致线圈内谐振电流呈非线性变化,这是导致传输效率随匝数增加而非线性变化的直接原因。同时,当系统传输效率最大时,线圈内谐振电流并非为最大值,故此时的输出功率并非最大值,这也导致了系统传输能力也随线圈匝数增加呈非线性变化。
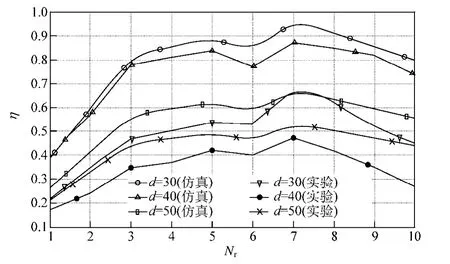
图6 η随Nr、d变化关系图Fig.6 η varies with Nr or d
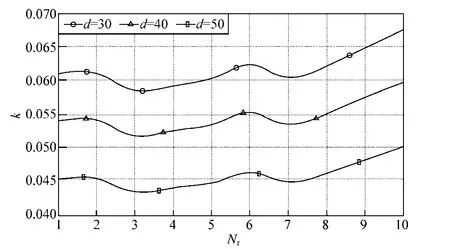
图7 k随Nr、d变化关系图Fig.7 k varies with Nr or d
由于线圈电感与其匝数并非呈正比关系,且线圈阻抗随匝数几乎呈正比增长,故当线圈匝数增大到一定值时,内阻对线圈内谐振电流的影响明显增大,故必存在一个最优匝数值,使得系统传输效率达到最大值。由图6可以看出,在能量发射线圈与能量接收线圈间距离固定时,接收线圈存在一个最优匝数值,使得系统能量传输层的传输效率最大,本文所设计系统中,Nr=7时,传输效率达到最大值,且发射线圈与接收线圈在不同的轴向距离下,接收线圈存在相同的匝数值使得传输效率最优化。但由于本文理论分析时忽略了辐射阻抗及趋肤效应的影响,加上实验中的不可抗误差,理论值与实验值存在一定的误差。由图7可明显看出,发射线圈与接收线圈间耦合系数在一定范围内存在极值点,但随着接收线圈的匝数继续增加而呈上升趋势,这是由于接收线圈电感随匝数增加呈非线性增长导致的。综合图 6、图7可知,系统能量传输层的传输效率与两线圈间的耦合程度并非呈正比关系,通过缩短传输距离,可以大幅度提高线圈间的耦合程度,同时也可以大大增加系统传输效率。相反,当传输距离确定时,决定传输效率最主要的因素是由线圈匝数增加而引起的线圈内阻、线圈间互感及线圈自身电感的变化,它们的变化会间接引起线圈内谐振电流的变化。
5 结论
本文通过对磁耦合无线电能传输系统进行建模分析,主要研究其系统能量层发射与接收线圈间的传输效率与接收线圈匝数间的关系,从而确定最大传输效率下的接收线圈匝数设计,即在系统其他参数固定情况下,接收线圈存在最优匝数值使得系统传输效率达到最大,且不同传输距离下的最优匝数值具有同一化的特点。通过缩短传输距离可以明显提高线圈间的耦合系数,更有助于系统传输效率的提高。针对系统传输效率性能指标,以上结论对磁耦合无线电能传输实际系统的搭建具有很好的指导意义。
[1]赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2012,32(3): 1-13.
Zhao Zhengming, Zhang Yiming, Chen Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Chinese Society for Electrical Engineering, 2012, 32(3): 1-13.
[2]杨庆新, 陈海燕, 徐桂芝, 等. 无接触电能传输技术的研究进展[J]. 电工技术学报, 2010, 25(7): 6-13.
Yang Qingxin, Chen Haiyan, Xu Guizhi, et al.Research progress in contactless power transmission technology[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 6-13.
[3]Tan Linlin, Huang Xuelang, Huang Hui, et al. Transfer efficiency optimal control of magneticresonance coupled system of wireless power transferbased on frequency control[J]. Science China, 2011, 54(6): 1428-1434.
[4]翟渊, 孙跃, 戴欣, 等. 磁共振模式无线电能传输系统建模与分析[J]. 中国电机工程学报, 2012,32(12): 155-160.
Zhai Yuan, Sun Yue, Dai Xin, et al. Modeling and analysis of magnetic resonance wireless power transmission systems[J]. Chinese Society for Electrical Engineering, 2012, 32(12): 155-160.
[5]黄学良, 吉青晶, 谭林林, 等. 磁耦合谐振式无线电能传输系统串并式模型研究[J]. 电工技术学报,2013, 28(3): 171-176.
Huang Xueliang, Ji Qingjing, Tan Linlin, et al. Study on series-parallel model of wireless power transfer via magnetic resonance coupling[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 171-176.
[6]Qiang Hao, Huang Xueliang, Tan Linlin, et al.Achieving maximum power transfer of inductively coupled wireless power transfer system based on dynamic tuning control[J]. Science China Technological Sciences, 2012, 55(7): 1886-1893.
[7]П·Л·卡兰塔罗夫, Л·А·采伊特林. 电感计算手册[M]. 陈汤铭, 刘保安, 罗应立, 等, 译. 北京:机械工业出版社, 1992.
[8]Ki Bong Kim, Zivan Zabar, Leo Birenbaum. Mutual inductance of noncoaxial circular coils with constant current density[J]. IEEE Transactions on Magnetics,1997, 33(5): 4303-4309.
[9]傅文珍, 张波, 丘东元, 等. 自谐振线圈耦合式电能无线传输的最大效率分析与设计[J]. 中国电机工程学报, 2009, 29(18): 21-26.
Fu Wenzhen, Zhang Bo, Qiu Dongyuan, et al.Maximum efficiency analysis and design of selfresonance coupling coils for wireless power transmission system[J]. Chinese Society for Electrical Engineering, 2009, 29(18): 21-26.
[10]黄辉, 黄学良, 谭林林, 等. 基于磁场谐振耦合的无线电力传输发射及接收装置的研究[J]. 电工电能新技术, 2011, 30(1): 32-35.
Huang Hui, Huang Xueliang, Tan Linlin, et al.Research on transmitter and receiver of wireless power transmission based on magnetic resonance coupling[J]. Advanced Technology of Electrical Engineering and Energy, 2011, 30(1): 32-35.
[11]Zhong Wenxing, Lee Chi Kwan, Hui Ron. General analysis on the use of tesla’s resonators in domino forms for wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 261-270.

