具有恒压特性的磁共振模式无线供电系统

翟 渊 孙 跃 苏玉刚 王智慧 李玉鹏

（重庆大学自动化学院 重庆 400030）

1 引言

感应电能传输技术是基于电磁感应原理，以电磁场为媒介，利用现代电力电子能量变换技术、高频变换技术和借助现代控制理论的一种新型、实用、灵活的供电技术[1-5]，但传输距离仍局限在较小尺度范围内，直到2007年MIT的科学家提出了磁共振模式的无线电能传输原理并成功利用该理论在 2m范围内点亮一个 60W的灯泡，磁共振模式无线电能传输技术的研究才成为国内外学者研究的热点[6-10]。在实际应用中，通常要求系统输出给负载的电压保持恒定，较为典型的应用是针对不同的目标分别引入闭环负反馈控制，这里面主要包括一次侧控制以及二次侧控制：一次侧控制是在一次侧加入控制器，通过一次侧在线辨识或者通过射频通信方式获得负载及输出参数，然后通过调节一次输入电压、能量注入时间或者软开关工作点来控制一次侧发射线圈电流，从而使输出电压保持恒定[11,12]。二次侧控制是通过在二次侧加入Buck或者Boost型DC-DC变换器，实现对输出电压的恒定控制[13]。

为实现系统输出电压恒压，传统的闭环控制策略均能达到较好的效果，但是需要引入闭环控制，从而导致系统设计的难度增大，稳定性降低。本文拟在前人研究基础上，围绕 PSSS型磁共振模式无线供电系统，通过互感耦合模型推导出使系统具有自然恒压特性的参数边界条件，使得系统在所设计的负载范围内，能自然实现发射线圈谐振电流，负载两端输出电压均近似恒定，从而可以在没有控制器的条件下，达到实际应用的需求，简化了系统的设计，提高了系统运行的鲁棒性，仿真及实验结果验证了本文理论的正确性。

2 磁共振无线电能传输系统工作原理与拓扑分析

2.1 磁共振模式无线电能传输系统工作原理

典型的磁共振模式无线电能传输系统的原理图如图1所示，输入电源经过能量变换后由一次侧发射线圈进行电磁变换，一次侧共振环节感应到此磁场能量后把能量以无线方式传递到二次侧共振环节，接收线圈感应到二次侧共振环节的能量后进行磁电变换，变换后的电能经过调理供用电设备使用。

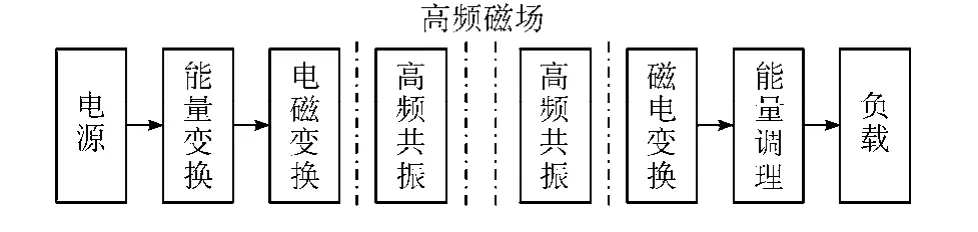
图1 磁共振模式无线电能传输系统的原理框图Fig.1 Block diagram of the magnetic resonance mode of wireless power transmission system

对于共振环节，由于没有接上电源以及负载，因此其拓扑结构固定，而发射和接收端则有不同的拓扑结构，本文以 PSSS型拓扑结构磁共振模式无线电能系统为研究对象。

2.2 PSSS型磁共振模式无线电能传输系统拓扑结构

为了实现系统的最大化能量传输，同时减少系统的无功功率容量，通常需要对发射端和接收端绕线电感进行补偿，共振线圈由于没有接负载和电源其拓扑结构固定为串联型结构，本文对 PSSS型拓扑结构进行分析介绍，也即发射端为并联补偿，接收端串联型补偿，其拓扑结构如图2所示。对于磁共振模式，电能的无线传输可在中距离下完成，所谓中距离也即共振线圈之间的距离可达到线圈直径的几倍以上[6]，此时发射线圈和共振线圈 2，发射线圈和二次侧接收线圈以及共振线圈1和二次侧接收线圈之间的互感可忽略不计。Edc是磁共振电能传输系统逆变电路的直流输入电压，Ls、Lr分别是共振线圈1和共振线圈2的电感，Cs、Cr是其相应的补偿电容，Cp、Cl分别是发射端和接收端电感Lp、Ll的补偿电容，Rp、Rl分别是发射端和接收端的等效串联电阻，Rs、Rr分别是共振线圈1，2的等效串联电阻，Req为等效负载，Uo为系统输出电压。Mps为发射端和共振线圈1之间的互感系数，Msr为两共振线圈之间的互感系数，Mrl为共振线圈2和接收端之间的互感系数。由于发射端为并联补偿，因此电压源Edc通过串联大电感Ldc形成准电流源，经开关网络 S1~S4逆变为准方波电流源，驱动一次侧谐振网络在能量发射线圈Lp上产生交变电流，激发高频磁场。

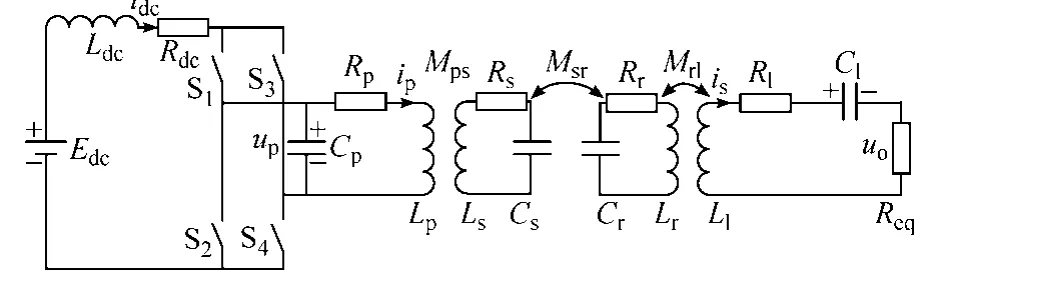
图2 PSSS型磁共振系统Fig.2 Magnetic resonance system of PSSS

3 系统输出功率和效率计算输出特性

高频下线圈损耗电阻主要包括欧姆损耗电阻Ro和辐射损耗电阻Rra，对于磁共振模式电能传输系统，Rra远小于Ro[9]，此时可忽略辐射损耗，由于线圈的阻抗相对于负载来说也很小，为简化分析此时也忽略线圈自身的内阻。

根据互感原理，对于 PSSS型拓扑结构，在四个线圈均处于谐振状态，谐振角频率为ω0，且逆变器输入电压为Edc情况下，共振线圈2，共振线圈1以及一次侧发射线圈的反射阻抗zrl、zsr、zps分别为

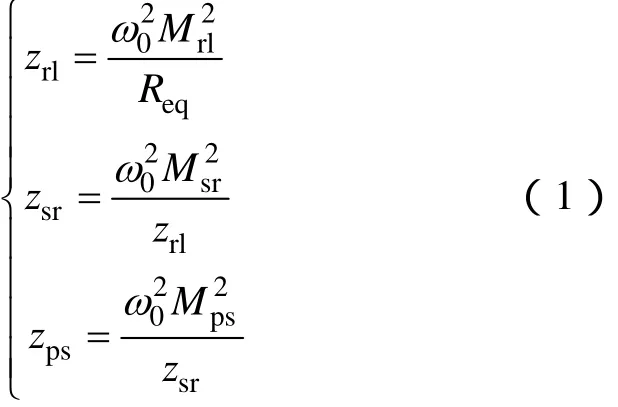
由式（1）经过化简，可得到系统的反射阻抗为

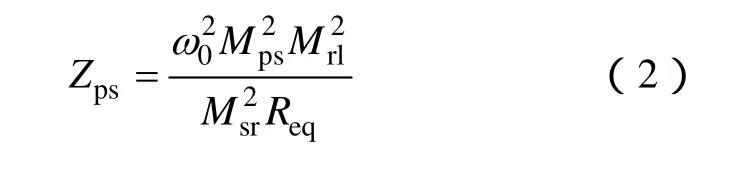
从而得到一次线圈的电流为

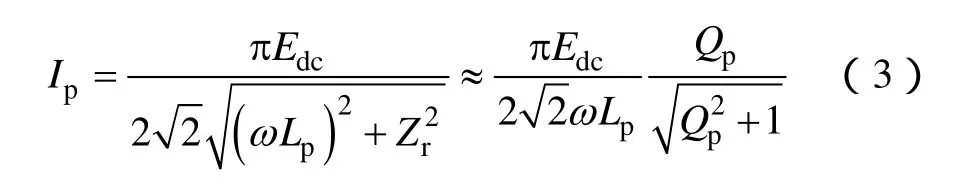
式中，Zr为一次谐振回路后端网络的反射阻抗；Qp为一次谐振网络的品质因数。

当满足Qp＞3，即等效负载Req满足边界约束条件时

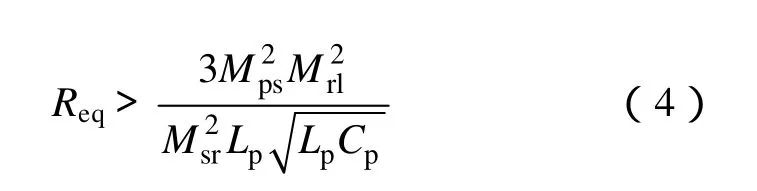
此时，PSSS型磁共振模式无线电能传输系统一次谐振电流Ip保持近似恒定，且其恒定的电流值为

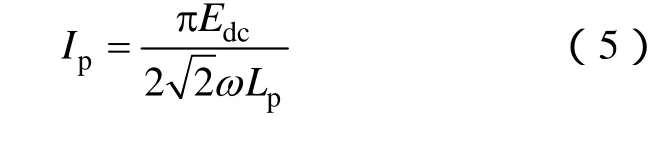
对于图2所示的磁共振系统，由交流阻抗法可得输出端谐振网络电流有效值为

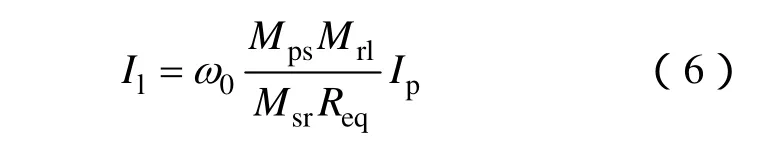
此时二次谐振网络电流Il是与Req有关的一个变量，Req两端的电压Uo为

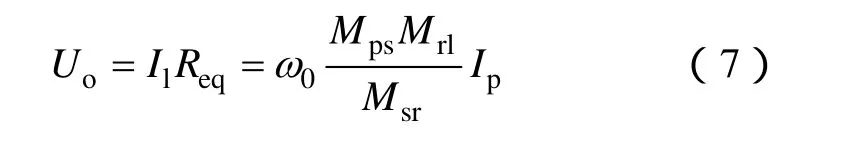
因此，当系统满足式（4）的条件时，负载发生变化时发射线圈电流保持恒定，由式（7）可知，当系统工作在恒频模式且线圈间距离保持不变的情况下系统输出电压Uo与负载阻抗值Req无关，系统负载输出电压恒定。当系统不满足式（4）所要求的临界条件时，在不增加控制器的条件下系统输出电压不能保持恒定，而是随着负载变小而逐渐减小。在实际系统设计中，若系统会工作在重载条件下，随着负载的变小系统可能会不满足临界条件，此时可通过合理设计参数如改变线圈间的互感、系统的工作频率等措施来改变系统的临界条件，从而使得系统能够在所要求的工作范围内具有自然恒压特性。

4 仿真与实验研究

为验证上述磁共振电能传输理论分析的正确性，搭建了一个工作频率为200kHz的PSSS型的磁共振无线电能传输系统仿真模型，对系统的输出恒压特性进行仿真设计，仿真中各主要元件参数见表。

表 磁共振电能传输系统仿真参数值Tab. Parameters of simulation of the magnetic resonance system

假设系统输入直流电压为Edc=310V，系统工作频率为 200kHz，Mps=3.2μH，Msr=0.9μH，Mrl=3.1μH，由式（4）计算可知，系统的临界电阻为 29Ω，用两个阻值和功率分别为 50Ω/200W，100Ω/200W 的电阻来作为系统的负载，由于这两个负载均大于29Ω，因此满足系统输出恒压的临界条件。初始负载为两个电阻串联，在t=3.5μs时把 100Ω 负载短路。在Simulink中按照上述参数建立磁共振系统的仿真模型，得出如图3所示的仿真结果。图3所示的分别是一次发射线圈电流有效值、负载输出电压的仿真图，t=3.5μs时负载由150Ω切换到50Ω。

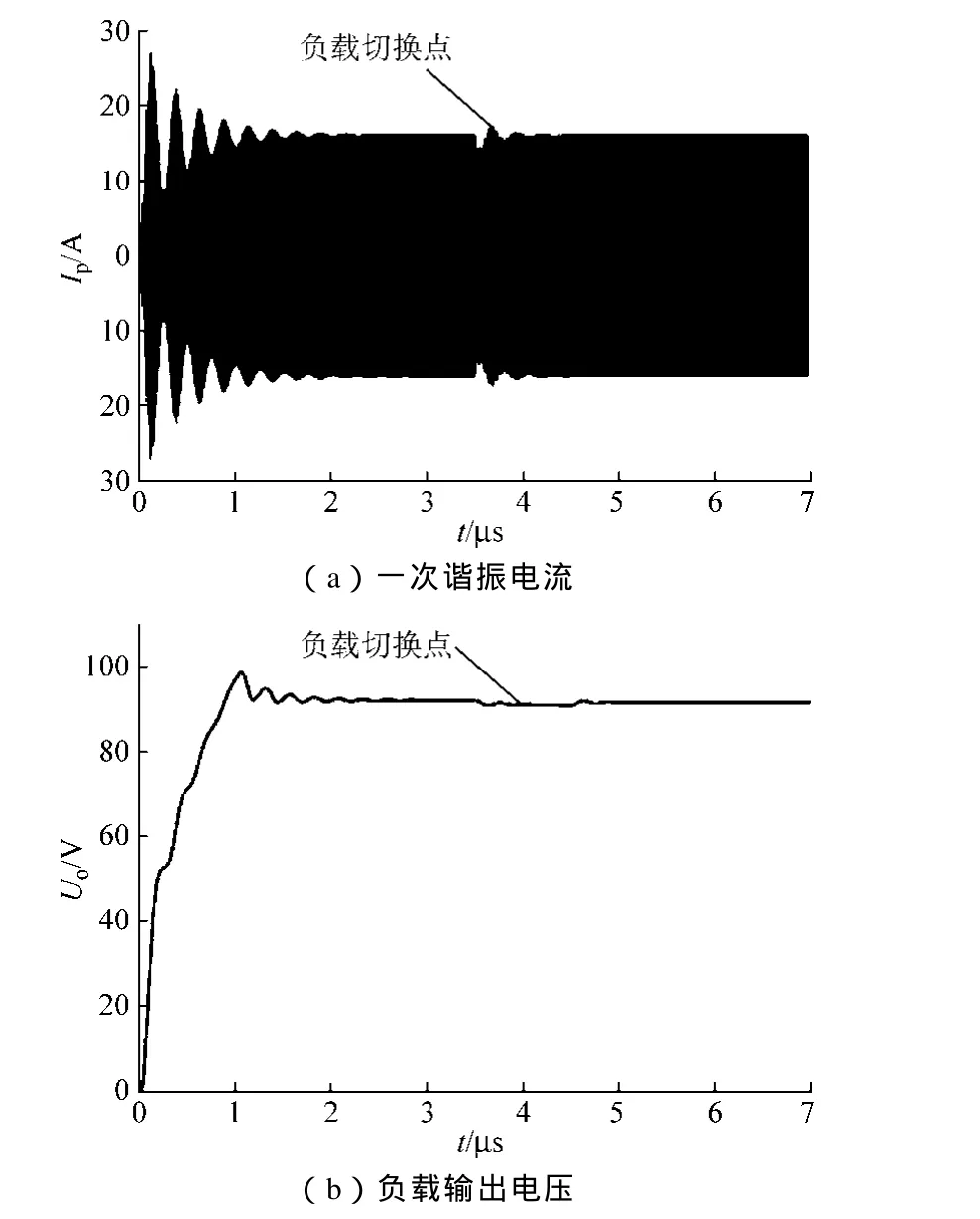
图3 系统仿真结果图Fig.3 Results of simulation system

由图3a可知，当负载切换时，一次谐振电流基本保持不变，由图3b可知，当负载由60W切换到160W，负载输出电压保持很好的恒定性；由于磁共振模式不允许浮频控制，系统工作频率应保持恒定，系统必须工作在恒频驱动模式，驱动频率为200kHz。仿真结果显示，当负载满足式（4）所要求的边界条件时磁共振模式无线供电系统具有自然恒压的电压输出特性。

为验证理论分析的正确性，按照表所示参数搭建一个工作频率为200kHz的磁共振模式试验系统，负载切换过程实验波形如图4所示，当负载从150Ω切换 50Ω，一次谐振电流有效值由 11.7A变化到11.6A，谐振电流有效值变化率仅为0.08%，因此可认为系统一次谐振电流处于恒流状态；负载输出电压平均值由 94.7V变化到 92.1V，电压变化率为2.7%，实现了负载输出电压的恒定。

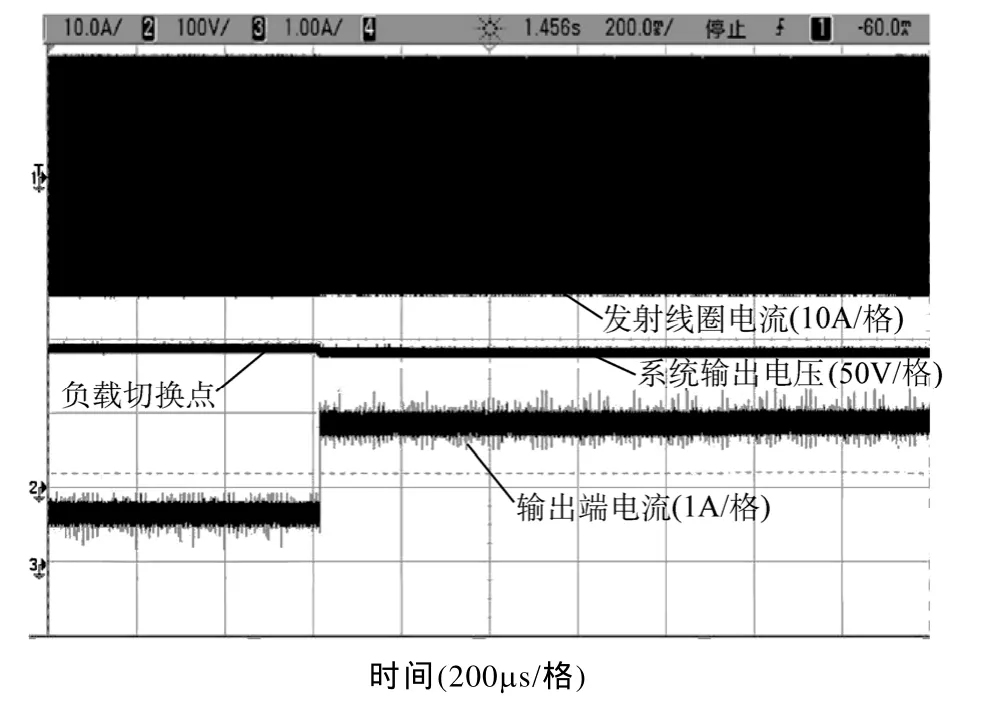
图4 负载切换过程实验波形Fig.4 Experimental waveforms as the load changes

系统的传输效率也是无线电能传输系统中需要关心的重要指标。在系统其他参数不变的情况下，从低于临界负载开始逐步增大系统的负载，得到负载变化与传输效率的曲线如图5所示。从图中可以看出随着负载的增大，电路的传输效率在逐渐减小，这是由于在轻载条件下，随着负载的变轻，电路本身会消耗越来越多的功率，因此系统的传输效率在逐渐减小。由于在重载条件下系统的输出电压已经不再恒定，为达到恒定输出的效果还需增加相应的控制电路或电压转换电路，这势必会降低系统的效率以及增加系统的复杂性，因此在实际应用中应根据式（4）合理设计参数来确保系统在重载条件下仍能满足恒压边界条件，使系统在要求的功率范围内均拥有恒压输出特性。

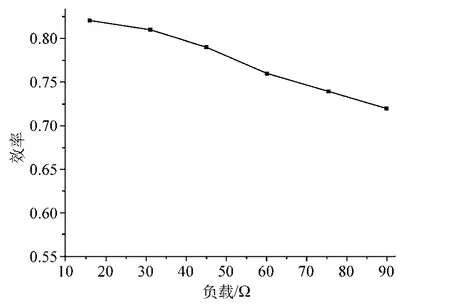
图5 输出功率随负载变化曲线图Fig.5 Curve of the output power as the load changes

5 结论

本文基于互感模型对 PSSS型磁共振模式无线电能传输系统的发射线圈电流，负载输出电压的特性进行了分析，给出了使系统能够恒流恒压工作的边界条件。由于磁共振模式的共振线圈具有很高的Q值，因此共振线圈的共振频率要保持恒定，否则系统的传输功率会急剧下降，这就要求磁共振系统必须恒频驱动。当系统恒频运行时，在不改变线圈之间距离的条件下，当负载满足本文所提出的边界条件时，不需要增加控制器便能够使得系统工作在恒流恒压状态。此方法不需复杂的控制策略，易于实现，具有较好的实际应用价值。

[1]Sallan J, Villa J L, Llombar A, et al. Optimal design of ICPT systems applied to electric vehicle battery charge[J]. IEEE Transactions on Industrial Electronics,2009, 56(6): 3060-3068.

[2]Green A W, Boys J T. 10kHz inductively coupled power transfer-concept and control[J]. Power Electronics and Variable Speed Drives, 1994, 399: 694-699.

[3]Bingnan W, Koon H T, Nishino T, et al. Experiments on wireless power transfer with metamaterials[J].Applied Physics Letters, 2011, 98(25): 1-3.

[4]Tang C S, Sun Y, Su Y G, et al. Determining multiple steady-state ZCS operating points of a switch-mode contactless power transfer system[J]. IEEE Transactions on Power Electronics, 2009, 24(1-2): 416-425.

[5]夏晨阳, 孙跃, 贾娜, 等. 耦合磁共振电能传输系统磁路机构参数优化[J]. 电工技术学报, 2012.27(11): 139-145.

Xia Chenyang, Sun Yue, Jia Na, et al. Magnetic circuit parameter optimization for coupled magnetic resonances power transfer system[J]. Transactions of China Electrotechnical Society, 2012, 27(11):139-145.

[6]Aristeidis Karalis, Joannopoulos J D, Marin Soljacic.Efficient wireless non-radiative mid-range energy transfer[J]. Annals of Phisics, 2007, 323(1): 34-48.

[7]Zhang Xiu, Zhao Yanpu, Ho S L, et al. Analysis of wireless power transfer system based on 3-D finiteelement method including displacement current[J].IEEE Transactions on Magnetics, 2012, 48(11): 3692-3695.

[8]Kiani M, Ghovanloo M. The circuit theory behind coupled-mode magnetic resonance-based wireless power transmission[J]. IEEE Transactions on Circuits and System, 2012,59(9): 2065-2074.

[9]Soljačić M, Kurs A, Karalis A, et al. Wireless power transfer via strongly coupled magnetic resonances[J].Sciencexpress, 2007, 112(6): 1-10.

[10]Rafif E Hamam, Aristeidis Karalis. Coupled-mode theory for general free-space resonant scattering of waves[J]. Physical Review A, 2007, 75(5): 1-5.

[11]戴欣, 孙跃, 等. 感应电能传输系统参数辨识与恒流控制[J]. 重庆大学学报, 2011, 34(6): 98-104.

Dai Xin, Sun Yue, et al. Study on constant current control of inductive power transfer with parameter identification[J]. Journal of Chongqing University,2011, 34(6): 98-104.

[12]唐春森. 非接触电能传输系统软开关工作点研究及应用[D]. 重庆: 重庆大学, 2009.

[13]Huang C Y, Boys J T, Covic G A. Practical considerations for designing IPT system for EV battery charging[C]. IEEE Vehicle Power and Propulsion Conference, Michigan, USA, 2009: 402-407.