考虑橡胶支座作用的桥梁多次竖向碰撞力的计算

杨海波， 尹晓春

(南京理工大学 力学与工程科学系，南京 210094)

地震诱发的桥梁结构碰撞破坏受到了工程界的高度关注。由水平地震诱发的邻桥之间、桥面与桥台之间的水平碰撞力[1]和桥梁水平碰撞响应等[2-3]已经得到了详细的研究，而竖向地震诱发的桥梁结构碰撞现象研究得非常少。

为了抵抗竖向重力荷载，桥梁结构的竖向刚度一般设计得较大，安全系数相对较高[4]。大量远场地震数据也显示，竖向地震的加速度分量要明显小于水平地震的加速度分量[4-5]，因此，认为竖向地震的破坏作用是次要的[6]。然而，随着地震监测网的加密和监测手段的更新，越来越多的近场地震的监测数据表明，竖向地震加速度幅值超出了预期值。例如，Northbridge地震记录到的竖向加速度最大值为1.18g，竖向地震加速度与水平加速度的比值(V/H)最大达到了1.79[4]，Kobe地震地面竖向加速度峰值是横向加速度峰值的两倍[5]，四川汶川地震距离断层20km内的9条地震记录曲线显示V/H的平均值为0.89，最大值为1.2[7]。对近场地震数据进一步的分析发现，近场竖向地震加速度反应谱有其独有的特征。V/H与反应谱周期、震中距以及局部场地条件相关，在0.2s的短周期内，V/H有一个明显的峰值，它超过了规范给定的取值2/3[6]。

在实际地震中，竖向地震总是先于水平地震到达桥梁，两种地震激励峰值存在时间差trc。基于 Imperial Valley地震和Morgan Hill地震的监测数据，Collier[8]的研究表明，trc与震级、震中距、场地条件、传播路径和震源深度等密切相关。当震中距为20 km时，trc=3～4 s，当震中距为10 km时，trc=1～2s，当震中距为3 km时，trc≤0.5s[8]。在近场地震中，桥梁结构有可能在水平地震峰值尚没有到达之前就已发生损坏。因此，研究在高幅值近场竖向地震单独作用下，桥梁结构是否会发生竖向碰撞，以及碰撞力的幅值是十分必要的。

Tanimura等[9]曾认为桥梁上部结构发生跳起后再次落下发生的碰撞，是造成Kobe地震中Nielson桥支座发生断裂的主要原因。部分学者采用梁-柱单元与弹簧相结合的有限元模型，研究了水平地震单独作用或者有竖向地震参与的桥面水平碰撞[2-3]。最近，徐然等[10]采用梁-杆连续体模型，把碰撞力作为组合体的内力，计算了竖向地震作用下桥面和桥墩之间的碰撞力。但是，忽略了桥梁中的吸能构件，如桥梁支座等对碰撞的作用。而橡胶支座由于降低了桥梁结构的竖向刚度，延长了桥梁结构自振周期，可能对竖向地震能量的吸收和桥梁的动力响应产生明显的影响[11]。

本文采用连续梁模型和连续杆模型模拟桥面和桥墩，采用线性弹簧模拟橡胶支座，在近场竖向地震激励作用下，建立了研究桥梁竖向碰撞的梁-弹簧-杆模型。应用瞬态波函数展开法和组合体瞬态内力法，建立了竖向碰撞力的理论计算方法。并通过数值算例，研究了竖向地震激励周期和幅值，以及桥梁固有振动周期对竖向碰撞力的影响。

1 波动方程

图1所示为双跨连续梁桥模型。根据等刚度原则，将主梁简化为两端简支的等截面梁，桥墩简化为一端固结的等截面杆，桥墩上的橡胶支座简化为一端固结于桥墩上的线性弹簧。将桥梁上部结构自重作为均布外荷载q施加在主梁上，将竖向地震激励的作用效果采用基础运动B(t)来等效。设桥梁的长为2x0，横截面积为A，截面惯性矩为I，弹性模量为E，密度为ρ。设桥墩高为L，横截面积为Ar，弹性模量为Er，密度为ρr。桥梁橡胶支座的线弹性刚度为K。主梁采用Bernoulli-Euler梁模型，桥墩采用St. Venant杆模型。

图1 双跨连续梁桥模型

主梁AB和桥墩CD的波动方程为:

(1)

其中，y1(x,t)和y2(x,t)为主梁沿梁长的挠度分布，u(ξ,t)为桥墩沿墩高的轴向位移分布。

根据桥梁端点铰支、桥墩底部固结和地震激励B(t)，波动方程的边界条件为:

(2)

两段梁之间的挠度、转角和弯矩连续条件为:

(3)

主梁、支座和桥墩之间的位移和剪力连续性条件为:

u(L,t)-y1(0,t)=δ

(4a)

(4b)

式中，δ为弹簧的压缩量，F为橡胶支座的反力，也就是碰撞接触力。

若桥梁初始时刻处于静止无载状态，则主梁和桥墩的初始位移和初始速度分别为:

y1(x,0)=

y2(x,0)=

(5)

其中，Fs为初始时刻的支座静反力:

(6)

若桥面与橡胶支座之间发生了多次碰撞，则当碰撞力为零时，桥面脱离橡胶支座，进入分离过程。当桥面与橡胶支座再次接触在一起时，进入碰撞过程。在整个竖向地震作用过程中，被分割为若干个交替出现的分离过程和碰撞过程。主梁和桥墩在碰撞接触的支座处力的连续性和位移连续性条件为：

F=0,u≤y

(7)

F(u-y-F/K)=0

(8)

F=Qb2-Qb1,F>0

(9)

其中，Qb1和Qb2分别为从左端和右端计算的梁中部的剪力。式(7)表示了主梁和桥墩在分离过程中的力特性和位移特性，式(8)表示了桥面与橡胶支座的碰撞接触条件和分离条件，式(9)表示了碰撞接触过程中主梁和桥墩的力连续性条件，碰撞接触过程的位移连续性条件表示于式(8)中。

2 竖向碰撞力的计算方法

2.1 碰撞过程桥梁响应的理论解

在碰撞接触过程中，采用特征函数展开法[10,12-13]，把左、右跨梁的挠度分布和桥墩的轴向位移分布分解为准静态项和动态项:

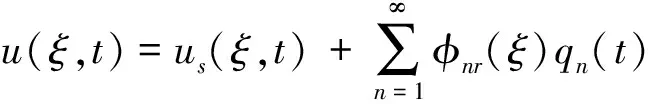
(10)

式中，φnb1，φnb2和φnr为左、右跨梁和桥墩的波模态函数，qn(t)为时间函数。准静态项满足静平衡方程、非齐次边界条件和连续性条件，动态项满足波动方程、齐次边界条件和连续性条件。准静态项和动态项叠加后的瞬态响应解满足波动方程、真实边界条件、连续性条件以及初始条件[12-13]。求解静平衡方程，容易得到准静态项的解ysi(x,t)和us(ξ,t)。

动态项是波模态函数和时间函数乘积的叠加，波模态函数由以下特征方程求解

(11)

根据特征方程(11)及其对应的齐次边界条件和连续性条件，以及主梁弯曲波模态和桥墩轴向波模态正交性和归一化条件[12-13]，由非平凡解存在的条件，可得到组合结构的共同频率方程为:

ErArkrncoskrnL(tankbnx0-thkbnx0)+

(12)

和波模态函数为:

如果发生了多次碰撞现象，则可设t*=t-t2k为第k次碰撞过程的时间变量，并设首次碰撞k=0，t2k为第k次碰撞的开始时间，由碰撞与分离条件(8)确定。将位移解(10)代入波动方程(1)，应用正交归一化条件，得到时间函数的微分方程，并采用Laplace积分变换方法，求出时间函数:

(14)

2.2 分离过程桥梁响应的理论解

在分离过程中，主梁和桥墩分别按照各自的波模态波动，而橡胶支座不受力，其求解方法与不考虑橡胶支座时相同[10]，本文不再叙述。在文献[10]中，第k次分离过程的初始位移和初始速度分布，同样为上次碰撞过程结束时刻的分布，因此，可以完成从碰撞过程到分离过程的连续求解。

2.3 碰撞力的计算方法

采用组合体瞬态内力法[10,13]，把碰撞过程的碰撞力看成是临时组合结构的内力，通过计算整个竖向地震激励过程的桥梁瞬态响应的理论解，提取作为内力的碰撞力，避免了求解强非线性方程和数值计算收敛性的问题。

可由桥墩上端面上的应力或弹簧的压力来计算出碰撞力:

(15)

式中,Γc为桥墩的上端面。

3 算例与分析

选择某高速公路两跨连续梁桥进行分析。该两跨连续梁桥的主梁采用预应力钢筋混凝土箱形梁，桥墩采用配有纵筋和螺旋箍筋的混凝土圆形柱。桥梁的单跨梁长为x0=38 m，根据公路钢筋混凝土及预应力混凝土桥涵设计规范[14]计算得到：主梁的换算截面面积A=6.4 m2，全截面换算惯性矩I=3.684 m4，混凝土标号为C40，弹性模量E=34.5 GPa，密度ρ=2 600 kg/m3，桥梁上部结构总重为1 948.34吨。桥墩的混凝土为C30，桥墩高度L=5.2 m，根据截面变形一致性假设，可计算得到等效弹性模量Er=31.7 GPa,等效面积Ar=3.077 2 m2，密度ρr=2 600 kg/m3。主梁和桥墩之间的板式橡胶支座的滞回曲线是狭长形的，可以近似简化为线性弹簧，弹簧刚度为K=2×109N/m。

由于复杂的地震激励可以用傅里叶级数展开为各谐波分量的叠加，如果能够求出单个谐波分量激励的响应形式，通过叠加方法即可求解全频谱地震激励下的响应。本文为简单起见，将竖向地震激励用主谐波分量的简谐运动代替。为了能够反映竖向地震的主要特征，将简谐运动的加速度峰值调整为竖向地震激励的加速度峰值。

为了研究在竖向地震单独作用下，桥梁结构是否会发生跳起和坠落碰撞现象，计算竖向碰撞力的变化特征，选取了不同的竖向地震反应谱进行研究。在场地为坚硬土层，震中距分别为3 km、10 km和20 km情况下，根据近场竖向地震反应谱特征的研究结果，选择适用的V/H谱形式[6]为:

(16)

在反应谱(16)中，α为V/H的峰值，β为线性衰减系数。当震中距为3 km时，α=1.5，β=5，trc= 0.5s；当震中距为10 km时，α=1.3，β=4，trc=2.0 s；当震中距为20 km时，α=1.1，β=3，trc=4.0s。

计算中选择在地震烈度为八度的地区，桥梁遭遇罕遇地震时的情况，取V/H的基准水平地震加速度峰值为510 gal(5.1 m/s2)[15]。

3.1 碰撞力随地震激励周期的变化

图2为反应谱(16)下的竖向碰撞次数和最大竖向碰撞/接触力随竖向地震激励周期的变化。计算结果显示，桥面与橡胶支座存在碰撞区和完全接触区两种形式。在碰撞区内，桥面发生跳起并脱离橡胶支座，坠落后与橡胶支座发生了竖向碰撞现象。在完全接触区内，桥面与橡胶支座始终接触在一起，没有发生桥面与橡胶支座的竖向碰撞。

仔细观察图2的计算结果可知，在水平地震加速度峰值尚未到达之前，也就是说在竖向地震激励单独作用的时段内，震中距分别为3 km、10 km和20 km的桥梁将发生1次、1～16次和1～36次的碰撞。最大竖向碰撞力的变化范围为23.11～72.70 MN，最大竖向碰撞力达7 270 t，为桥梁上部结构总重的3.73倍，说明竖向碰撞的确对桥梁具有危害作用。因此，在水平地震峰值到达之前，巨大的竖向碰撞力就有可能损坏桥梁结构。

在碰撞区内，桥梁的竖向碰撞次数多，竖向碰撞力急剧变化，并明显大于完全接触区的接触力。而在完全接触区内，桥面与橡胶支座的接触力变化缓慢，幅值较小。

图2 碰撞次数和最大碰撞/接触力(x0=38m)

图2的计算结果显示出一个重要的、奇特的现象，就是竖向碰撞现象集中发生在一个较窄的竖向地震激励周期范围内。图2表明该碰撞区范围为T=0.19～0.29 s，激励周期跨度区间仅为0.1 s。

3.2 碰撞力随桥梁固有频率的变化

理论计算图2参数桥梁的固有频率，可得到主梁的理论一阶弯曲振动周期为1.363 s，桥墩的理论一阶轴向振动周期为0.006 s，整座桥梁(桥梁-桥墩-橡胶支座)的理论一阶竖向振动周期Tb=0.236 s。对比分析可以发现，碰撞区位于Tb=0.236 s的附近，具体的竖向地震激励周期区间为80%Tb～120%Tb。因此，有理由怀疑当竖向地震激励周期逼近整座桥梁的固有振动周期时，会引发桥梁的大幅度振动响应，导致桥面跳起，从而产生显著的竖向碰撞现象。

图3给出了x0=38 m时，在竖向地震激励周期T=0.22 s激励下的桥梁响应曲线，包括碰撞/接触力、主梁碰撞端(中端)位移和桥墩碰撞端(顶端)位移响应曲线。计算中，取震中距为10 km的V/H谱(16)形式。图3清楚地显示，当竖向地震激励周期逼近桥梁的固有振动周期时，主梁的位移响应幅值明显加大，桥面的最大抛起量甚至达到35.0 mm。桥面的上抛导致与橡胶支座脱离跳起，然后下落剧烈碰撞橡胶支座，所产生的最大碰撞力为49.4 MN，达到了初期接触力的2.87倍。

为了进一步验证上述观点，增加计算桥梁单跨长度分别为25 m和45 m时的竖向碰撞力。当x0=25 m时，桥梁的整体固有振动周期Tb=0.123 s。当x0=45 m时，Tb=0.320 s。

图4计算结果表明，计算得到的碰撞区分别为：当x0=25 m时，T=73%Tb～178%Tb；当x0=45 m时，T=91%Tb～125%Tb。另外，在图3中，划分出了阴影部分的高幅值碰撞力区，它们分别为：当x0=25 m时，T=81%Tb～146%Tb；当x0=45 m时，T=91%Tb～119 %Tb。显然，x0=25 m和x0=45 m时的窄碰撞区特征，以及位于桥梁固有振动周期附近的特征，与x0=38 m时完全相同。

表1 桥梁周期Tb

如果进一步将单跨梁长x0从20 m变化到50 m，桥梁的固有振动周期也随之从0.095 7 s变化到0.391 s，其变化幅度达到400%之多(见表1)，并且，选择竖向地震激励周期分别为T=0.1 s、0.2 s和0.3 s，竖向地震激励反应谱为距震中20 km的V/H谱(16)形式，则可扫描计算竖向碰撞力随桥梁固有振动周期的变化，计算结果见表2和图5。

表2 碰撞区特性

由图5的计算结果可以计算出以单跨梁长表达的碰撞区和高幅竖向碰撞力区，以及高幅竖向碰撞力区的Tb/T，并列于表2中。可以发现，竖向碰撞区和高幅值碰撞力区同样位于竖向地震激励周期T与桥梁固有振动周期Tb相互逼近的区间。

图5 不同桥跨跨径下的碰撞次数和最大碰撞/接触力

综合§3.1和§3.2的研究结果表明，剧烈的竖向碰撞现象与T逼近Tb显著相关。

由于影响地震激励周期的因素多，地震激励周期变化大，桥梁的固有振动周期难以避开地震激励周期，因此，如果桥梁结构设计没有考虑振动特性的话，在竖向地震激励的作用下，桥梁结构发生竖向碰撞现象，并出现高幅值竖向碰撞力有一定的必然性。

3.3 碰撞力随竖向地震激励幅值的变化

为了研究竖向地震激励幅值对竖向碰撞力的影响，图6给出了单跨梁长x0=38 m的桥梁，在竖向地震激励周期分别为T=0.1 s、0.2 s和0.3 s时的碰撞次数和碰撞力随竖向地震激励幅值的变化。

当地震激励周期为T=0.1 s时，由于T与Tb= 0.236 s相距较远，所以，在V/H从0.1到2.0的变化范围内，桥梁始终没有发生竖向碰撞现象，桥面和橡胶支座一直处于完全接触状态，接触力随着竖向地震激励的增大而线性地缓慢增加。

当地震激励周期为T=0.2 s和0.3 s时，由于T与Tb= 0.236 s比较逼近，桥梁发生了竖向碰撞现象。但是，对于T=0.2 s的情况，只有当V/H超过0.5时，才会发生竖向碰撞；对于T=0.3 s的情况，只有当V/H超过0.7时，才会发生竖向碰撞。这说明，尽管T逼近了Tb，仍然需要竖向地震的激励幅值达到某个阀值，竖向碰撞现象才会发生。

图6 不同V/H下的碰撞次数和最大碰撞/接触力

图6的计算结果表明，碰撞次数随竖向地震激励幅值的变化并不是单调增加的，而最大碰撞力基本上是随V/H的增大而增加。

4 结 论

本文考虑橡胶支座的作用，建立了梁-弹簧-杆模型，采用瞬态波函数展开法和组合体瞬态内力法，提出了桥梁结构在竖向地震激励下的竖向碰撞力的理论求解方法，计算结果表明本文方法可以合理地求解桥面与橡胶支座的多次竖向碰撞力。

通过对不同竖向地震反应谱、不同桥梁跨度和不同竖向地震激励幅值下的碰撞次数和碰撞力的计算和分析，可以得到以下结论：

(1)在浅源近场V/H竖向地震反应谱下，桥梁可能出现竖向碰撞现象，竖向碰撞力的幅值大，对桥梁具有相当大的危害。

(2)并非在所有情况下桥梁都会发生竖向碰撞现象，只有当竖向地震激励周期与桥梁整体结构的固有振动周期逼近，并且竖向地震激励幅值超过某个阀值时，才会出现竖向碰撞现象。

(3)竖向碰撞力与竖向地震激励周期、幅值和桥跨长度呈现出复杂的非线性关系。

参 考 文 献

[1]Malhotra P K. Dynamics of seismic pounding at expansion joints of concrete bridges [J]. Journal of Engineering Mechanics, 1998, 124(7): 794-802.

[2]Kim S H, Lee S W, Mha H S. Dynamic behaviors of the bridge considering pounding and friction effects under seismic excitations [J]. Structural Engineer Mechanics, 2000, 10(6): 621-633.

[3]王军文，李建中，范立础. 非规则梁桥横桥向地震碰撞反应分析[J]. 振动与冲击,2010, 29(6): 25-30.

WANG Jun-wen, LI Jian-zhong, FAN Li-chu. Analysis on pounding effect of irregular girder bridge under transverse earthquake [J]. Journal of Vibration and Shock, 2010, 29(6): 25-30.

[4]Papazoglou A J, Elnashai A S. Analytical and fileld evidence of the damaging effect of vertical earthquake ground motion [J]. Earthquake Engineering and Structural Dynamics, 1996, 25(10): 1109-1137.

[5]Yang J, Lee C M. Characteristics of vertical and horizontal ground motions recorded during the Niigata-ken Chuetsu, Japan Earthquake of 23 October 2004 [J]. Engineering Geology, 2007, 94(1/2): 50-64.

[6]Bozorgnia Y, Campbell K W. The vertical-to-horizontal response spectral ratio and tentative procedures for developing simplified V/H and vertical design spectra [J]. Journal of Earthquake Engineering, 2004, 8(2): 175-207.

[7]Wang D, Xie L L. Attenuation of peak ground accelerations from the great Wenchuan earthquake [J]. Earthquake Engineering and Engineering Vibration, 2009, 8(2): 179-188.

[8]Collier C, Elnashai A S. A procedure for combining vertical and horizontal seismic action effects [J]. Journal of Earthquake Engineering, 2001, 5(4): 521-539.

[9]Tanimura S, Sato T, Umeda T. A note on dynamic fracture of the bridge bearing due to the great Hanshin-Awaji earthquake [J]. International Journal of Impact Engineering, 2002, 27(2): 165-175.

[10]徐 然，尹晓春. 竖向地震作用下桥面与桥墩的多次重碰撞力的计算[J]. 工程力学, 2010, 27(10): 124-130.

XU Ran, YIN Xiao-chun. Calculations of multiple pounding forces between girder and pier of bridges under vertical earthquakes [J]. Engineering Mechanics, 2010, 27(10): 124-130.

[11]叶爱君, 胡世德，范立础. 桥梁支座抗震性能的模拟分析[J]. 同济大学学报, 2001, 29(1): 6-9.

YE Ai-jun, HU Shi-de, FAN Li-chu. Simulation of seismic behavior for bridge bearings [J]. Journal of Tongji University, 2001, 29(1): 6-9.

[12]徐 然，尹晓春. 竖向地震作用下桥梁结构的瞬态波响应分析[J]. 振动与冲击,2012, 31(1): 49-55.

XU Ran, YIN Xiao-chun. Transient wave response analysis of a bridge under vertical earthquakes [J]. Journal of Vibration and Shock, 2012, 31(1): 49-55.

[13]Yin X C, Qin Y, Zou H. Transient responses of repeated impact of a beam against a stop[J]. International Journal of Solids and Structures, 2007, 44: 7323-7339.

[14]JTG D62-2004. 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京：人民交通出版社，2004.

[15]JB 50011-2001. 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2004.