环境激励下结构模态参数识别的改进ITD法

杨佑发， 李 帅， 李海龙

(1.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045；2.重庆大学 土木工程学院，重庆 400045)

近年来随机状态空间理论在结构系统识别的应用有了很大的发展，尤其是随机子空间辨识(Stochastic Subspace Identification, SSI)方法的出现使得激励未知的系统辨识(或工作模态分析)问题成为可能，其优点在于无需贵重的激励设别，不需要中断结构的正常使用[1]。张之颖等[2]利用随机减量技术和ITD方法相结合，从而有效地识别环境激励下建筑结构的模态参数。随机子空间法由于其不需要经过随机减量法或者NExT法得到结构的自由衰减曲线，且识别精度高等优点，得到了国内学者的广泛关注。任伟新[3]对15层钢筋混凝土建筑和钢拱桥进行了模态参数识别，通过对比得出结论：峰值法简单、快捷、适用，但精度不高；随机子空间法工作量大、耗时多，但识别精度高。徐良等[4]利用随机子空间法对虎门悬索桥进行了模态参数识别。章国稳等[5]提出了一种基于特征值分解的随机子空间算法，解决了数据驱动随机子空间法计算效率低下的问题，通过重庆朝天门大桥模型分析验证了该方法的计算效率。

随机子空间法[6-7]是一种时域模态参数识别方法。其主要思想是以状态空间模型为识别模型，以协方差为统计量，利用信号和噪声的不相关性来去除噪声，最后采用奇异值分解法来识别结构的模态参数。随机子空间法的识别精度高，但计算效率不高。ITD 法[8-9]是 S.R.Ibrahim 提出的一种利用结构自由振动响应的位移、速度或加速度时域信号来进行模态参数识别的方法。运用ITD法进行参数识别时必须先采用随机减量法或者自然激励技术(NExT法)得到数据的自由衰减曲线，而此过程会产生一定的误差，且这两种前处理方法的输出长度的取值方面有一定的人为主观影响，有时也会使得衰减曲线产生偏差。在这个情况下采用ITD法进行参数识别必然会产生误差。本文基于随机子空间算法和ITD 法的原理，提出了环境激励下结构模态参数识别的改进ITD法。

1 改进的ITD法

(1)ITD法的基本理论

一个多自由度系统的自由振动响应微分方程的解可以表示为：

{x(t)}N×1=[Φ]N×2N{est}2N×1

(1)

其中

{x(t)}=[x1(t),x2(t),…,xN(t)]T

(2)

[Φ]=[{φ1},{φ2},…,{φ2N}]

(3)

{est}=[es1t,es2t,…,es2Nt]T

(4)

(2)改进ITD法

随机子空间法中数据的协方差计算可以保留原始数据中的所有信息，同时去除了噪声，因此得到的Toeplitz矩阵中的数据可以作为ITD法的输入数据。这样不再需要进行随机减量法或者自然激励技术(NExT法)前处理，从而避免了这两种前处理方法的不准确性带来的误差。一般的随机子空间法的原理[10]，先是构造Hankel矩阵，然后定义输出协方差矩阵，再是对Hankel矩阵变换构建Toeplitz矩阵，即：

(5)

(6)

(7)

两者相除后，有：

(8)

为了降低噪声的影响，现将矩阵[A]采用双最小二乘解方法，即两种单边最小二乘法的平均值：

(9)

式中,[A]正是ITD法所要求解的特征矩阵。频率和阻尼比的求解就和ITD法完全相同了，即只要对[A]进行特征值分解：

[A][Φ]=[Φ][α]

(10)

式(10)是一个标准的特征值方程，矩阵[A]的第r阶特征值为esrΔt，相应的特征向量为特征向量矩阵[Φ]的第r列。设求的的特征值Vr为

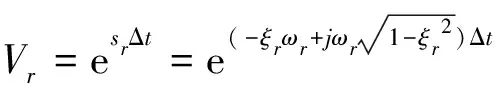
(11)

从而可以求得系统的模态频率和阻尼比分别为：

(12)

为计算系统的模态振型，需要先按式(13)求出测点p的第r阶模态留数为Arp：

(13)

2 改进的ITD法数值计算

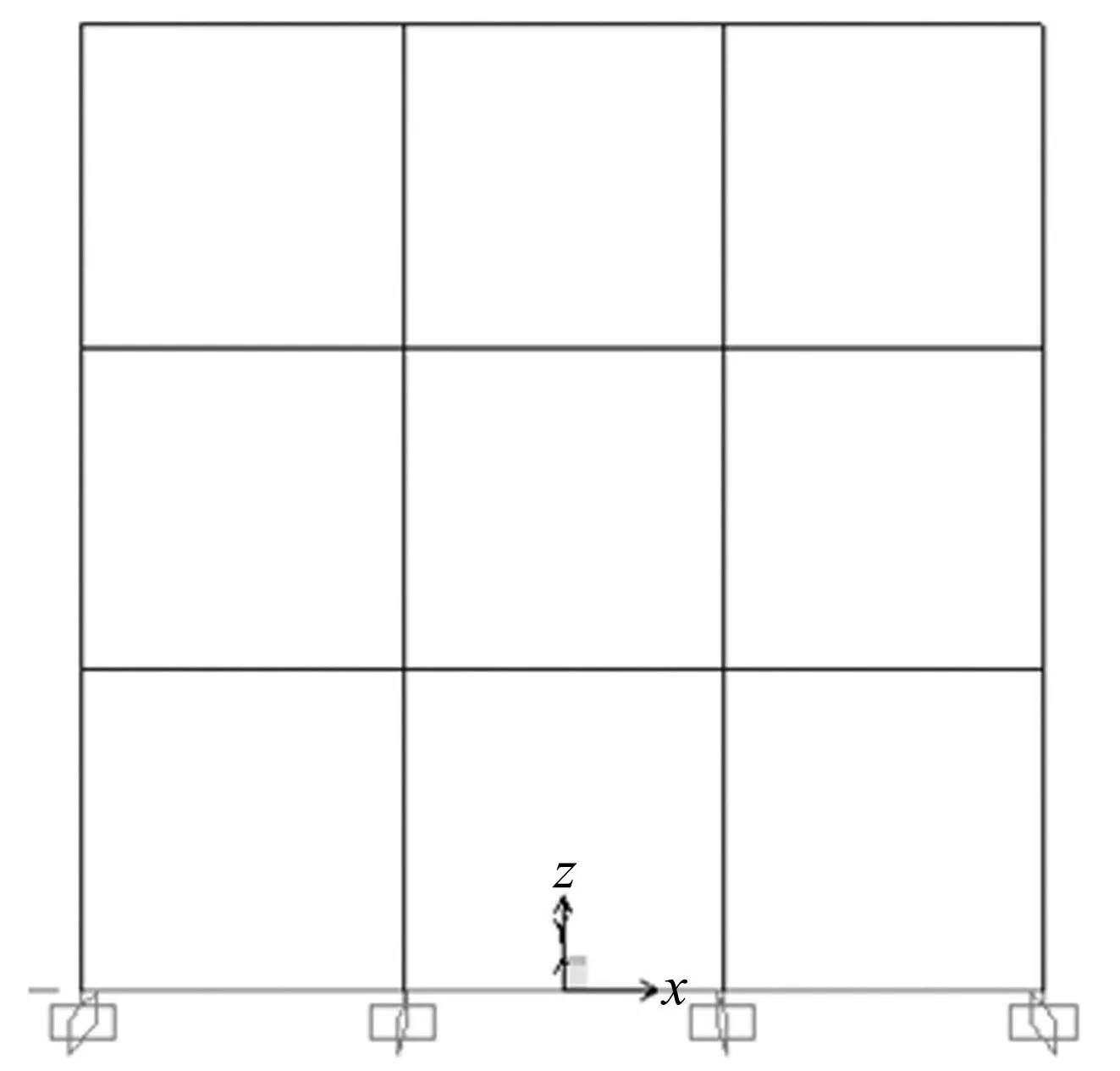
图1 框架模型

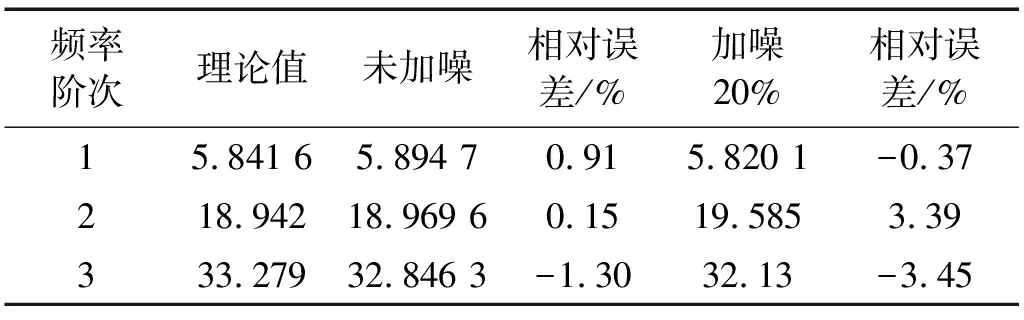
表1 改进ITD法频率识别值与理论值比较

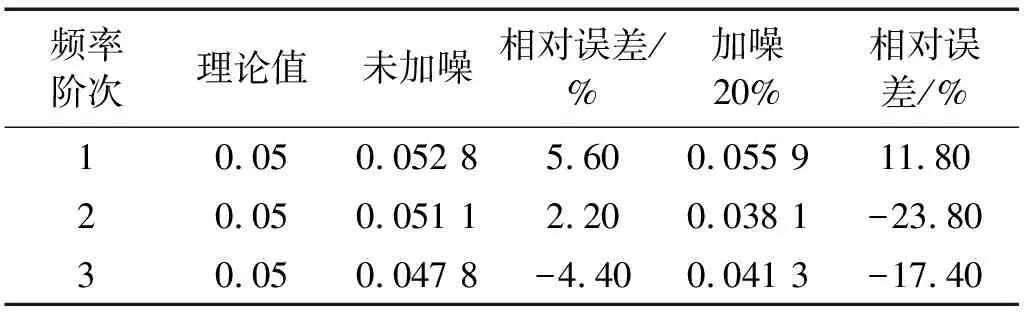
表2 改进ITD法阻尼比识别值与理论值比较

从表1和表2可以看出，用本文提出的改进ITD法识别频率值的精度非常高，加噪20%后的识别精度也能达到4%以内，识别的阻尼比值的精度也较高，说明此种方法的抗噪性能比较好，从而证明了改进ITD法理论的适用性。

3 框架结构模态辨识实验

实验模型为4层的剪切型钢框架结构，如图2所示，结构的外形尺寸为650(长)×400(宽)×1 700(高)mm，层高均为400 mm，1～4层楼板采用650×400×25 mm的钢板，底部连接钢板的尺寸为850×600×10 mm，每层柱采用4根375×60×5 mm(长×宽×厚)的扁铁。为了保证试验模型安装的可靠和连接的足够牢固，使用6根M12×60 mm的螺栓将模型底板锚固于实验室的钢梁上，柱和板之间焊接。实验所用的钢材的弹性模量为2.0×107N/m2，密度为7.85×103kg/m3。

图2 四层钢框架模型图

3.1 实验设备

主要的实验设备有：由扬州晶明科技有限公司生产的JM5840型号无线环境激励实验模态测试分析系统，主要用于动态信息的采集和分析。该仪器有三部分组成：即JM1801无线网卡、JM5840无线加速度传感器与JM5841无线振动节点和实验模态分析软件组成。

3.2 实验过程及数据采集

力锤锤击方向为沿板的长边方向，即沿Y向，现只记录Y方向的加速度响应信号， 35 s以后的响应信号可看作环境激励下的情况。采用一个传感器跑点的测量方法。具体操作流程是：

①先将传感器放到第四层，用力锤沿Y方向锤击第四层，测得加速度响应信号y44(第一个下标表示测点位置所在的楼层号，第二个下标表示激励所在的楼层号)；

②保持传感器放在第四层，用力锤沿Y方向锤击第三层，测得加速度响应信号y43，以此类推，得到y42、y41。

③将传感器放到第三层，同理分别锤击第四、三、二、一层，得到加速度响应信号y34、y33、y32、y31。

④同理将传感器放到第二、一楼层，依次可以得到其他加速度响应信号。

最终得到共计16条加速度响应曲线，限于篇幅所限，这里只给出传感器在第一层，分别锤击一、四层时的加速度响应曲线y12、y13如图3和图4所示。

3.3 数据处理

仪器测取的全是加速度数据，而前面所陈述的模态参数识别方法是针对位移数据的情况，所以先对加速度数据进行两次积分后得到位移数据。以加速度测量仪在第一层时的加速度数据y12、y13为例，对其两次积分后的位移曲线如图5和图6所示(z表示位移，第一个下标表示加速度测量仪所在的楼层号，第二个下标表示力锤锤击位置的楼层号)。

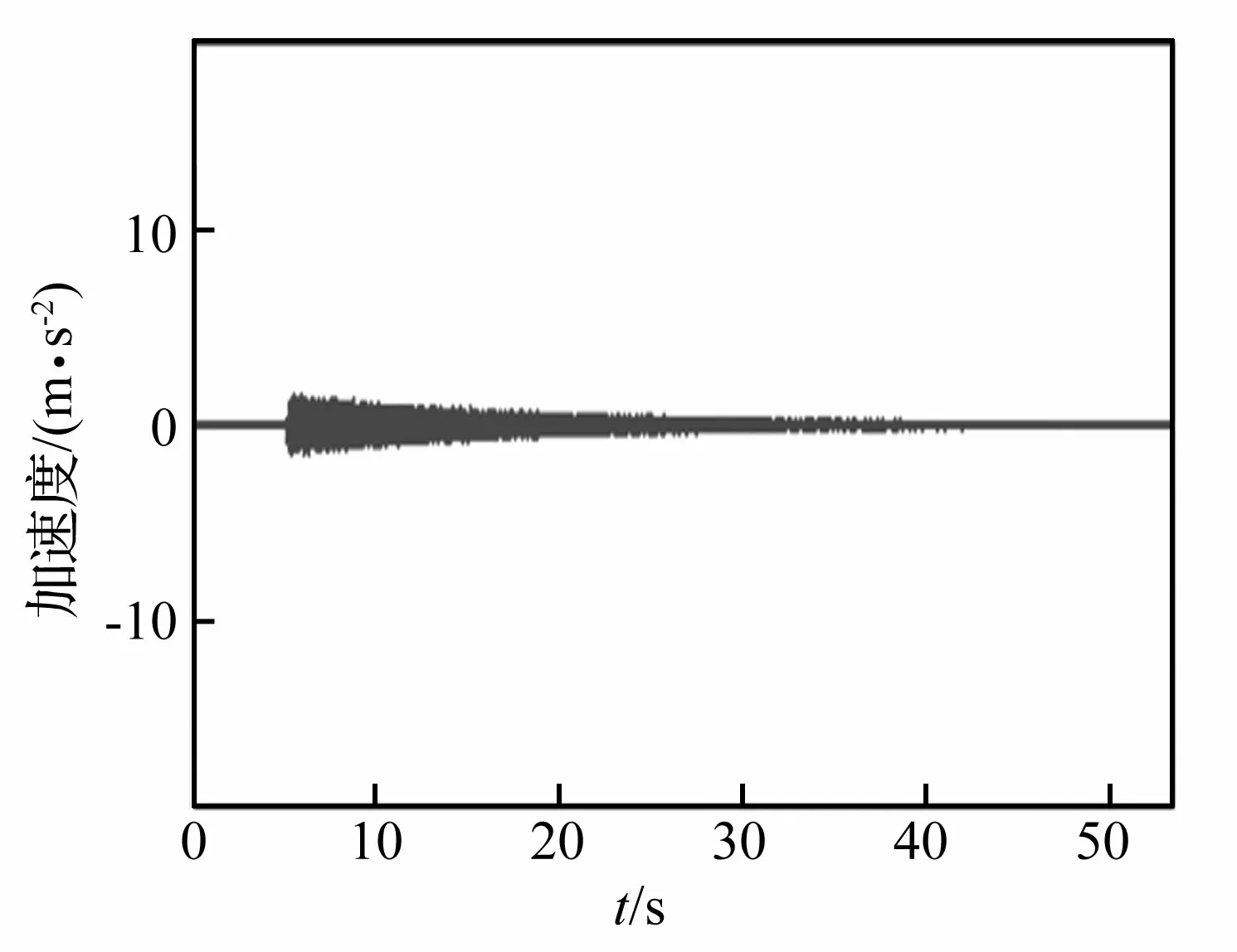
图3 加速度曲线y12

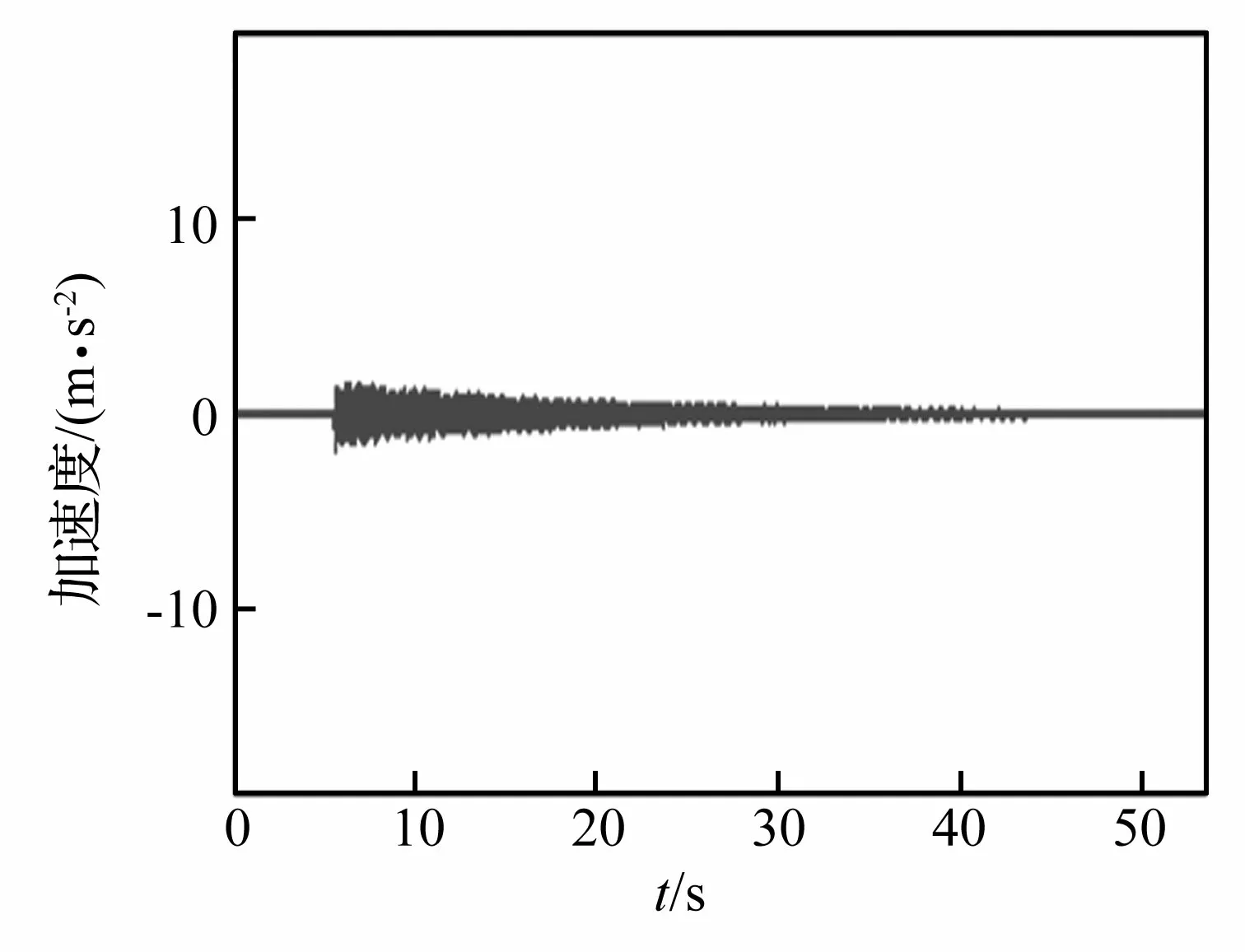
图4 加速度曲线y13

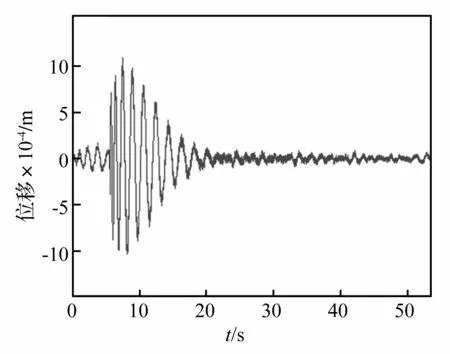
图5 位移曲线z12

将实验数据分成三段：第一段为锤击前的部分，即为钢框架结构在环境激励下的振动，大约在5或6 s以前的阶段；中间一段是钢框架在力锤敲击下的响应，大约在6 s以后到20 s之间的阶段；最后一段是20 s以后的阶段，仍可以看做是环境激励下的情况，为了完全排除力锤敲击的影响，结果分析时取35 s以后的响应信号。

3.4 环境激励下的模态参数识别

环境激励下钢框架的振动，比如加速度时程曲线y11的35 s以后的阶段，如图7；对应的位移曲线z11的35 s以后的阶段如图8所示。

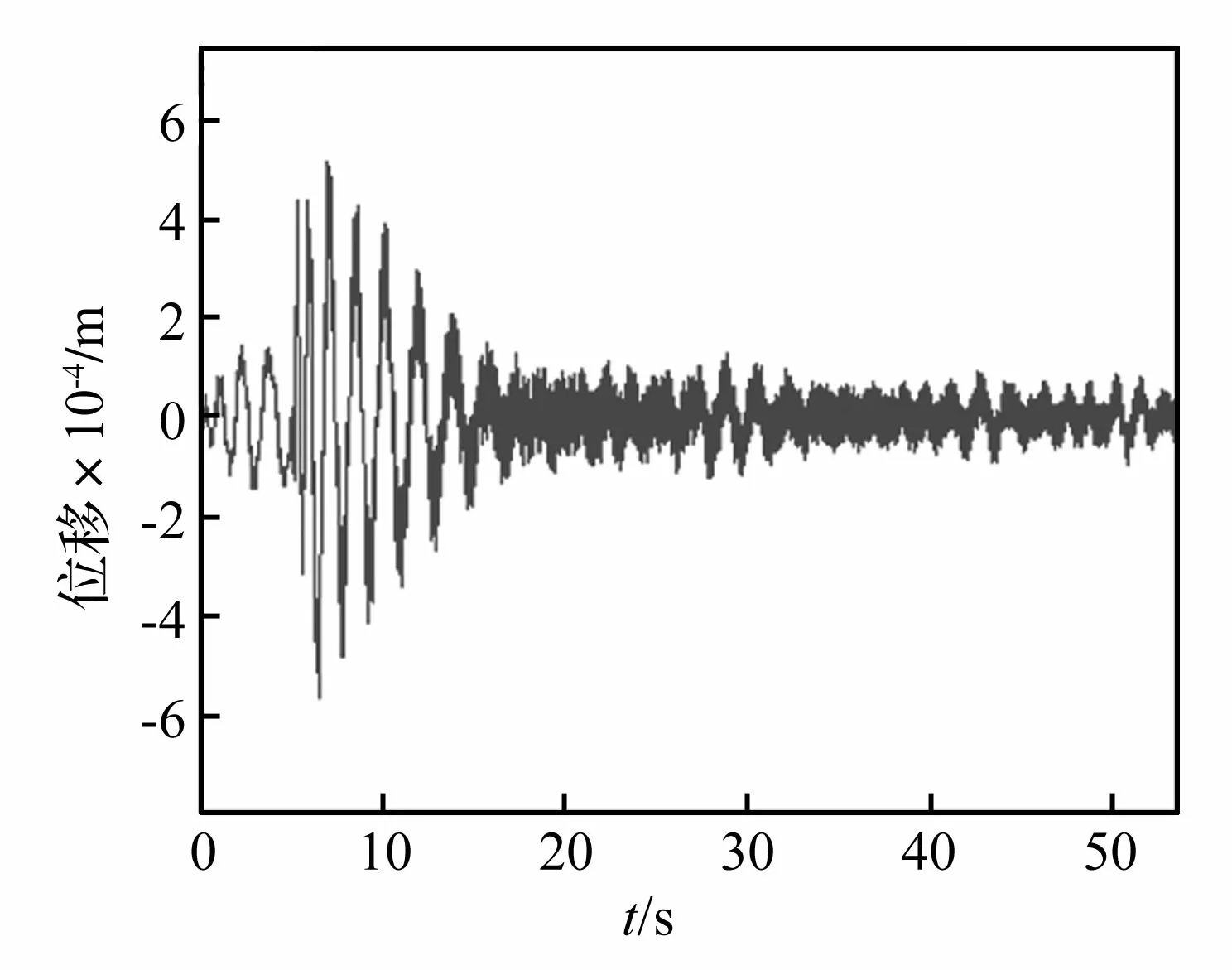
图6 位移曲线z13

图7 加速度曲线y11的35 s后时程图

图8 位移曲线z11的35 s后时程图

将环境激励下加速度仪所测得的每层楼的加速度时程曲线(4条)积分后，得到每层楼的位移时程曲线(4条)，以第一层楼的位移值为参考点，取35 s到50 s间的数据，分别得到一二三四层楼对第一层楼的相关函数。限于篇幅所限，这里只给出一、四层楼对第一层楼的相关函数曲线如图9和图10所示。

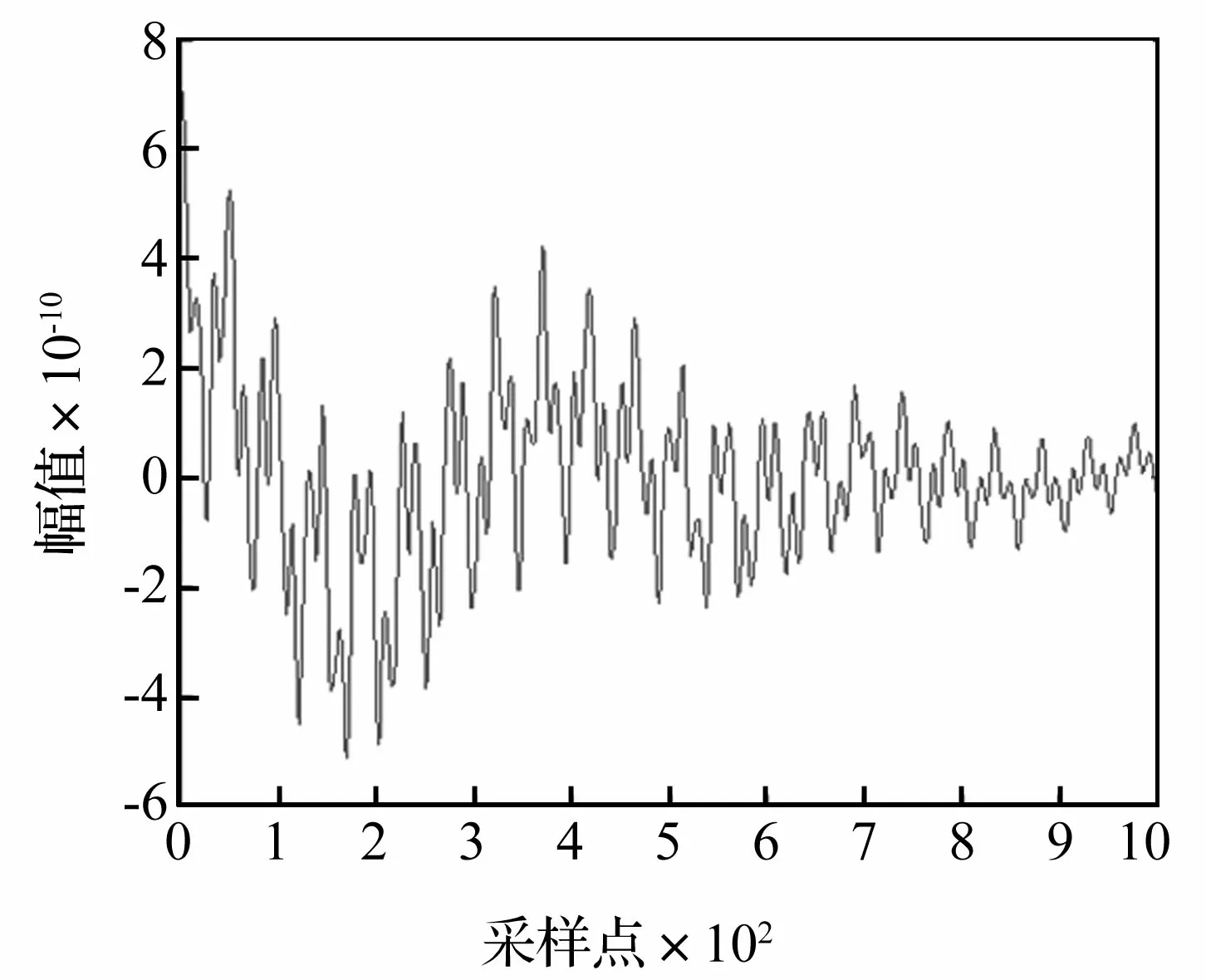
图9 一、一层位移相关函数曲线

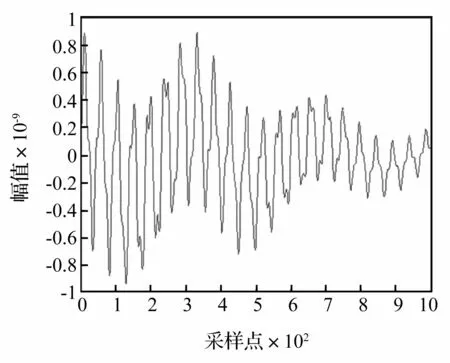
图10 一、四层位移相关函数曲线

直接运用协方差驱动SSI法识别时，稳定图如图11所示。当加速度仪放置在第一层，锤击位置为第四层时的位移响应数据为z14，取z14中35 s到50 s之间的数据作为环境激励下的响应，仅用单测点数据来识别。首先组建Hankel矩阵，取矩阵大小为1 000×1 000，再通过变换构造Toeplitz矩阵，Toeplitz也是1 000×1 000，取其任意行或列组成行(列)向量，作为ITD法的输入数据，采用改进 ITD法来进行模态参数识别,所求得的频率值与阻尼比值分别如表3和表4所示。

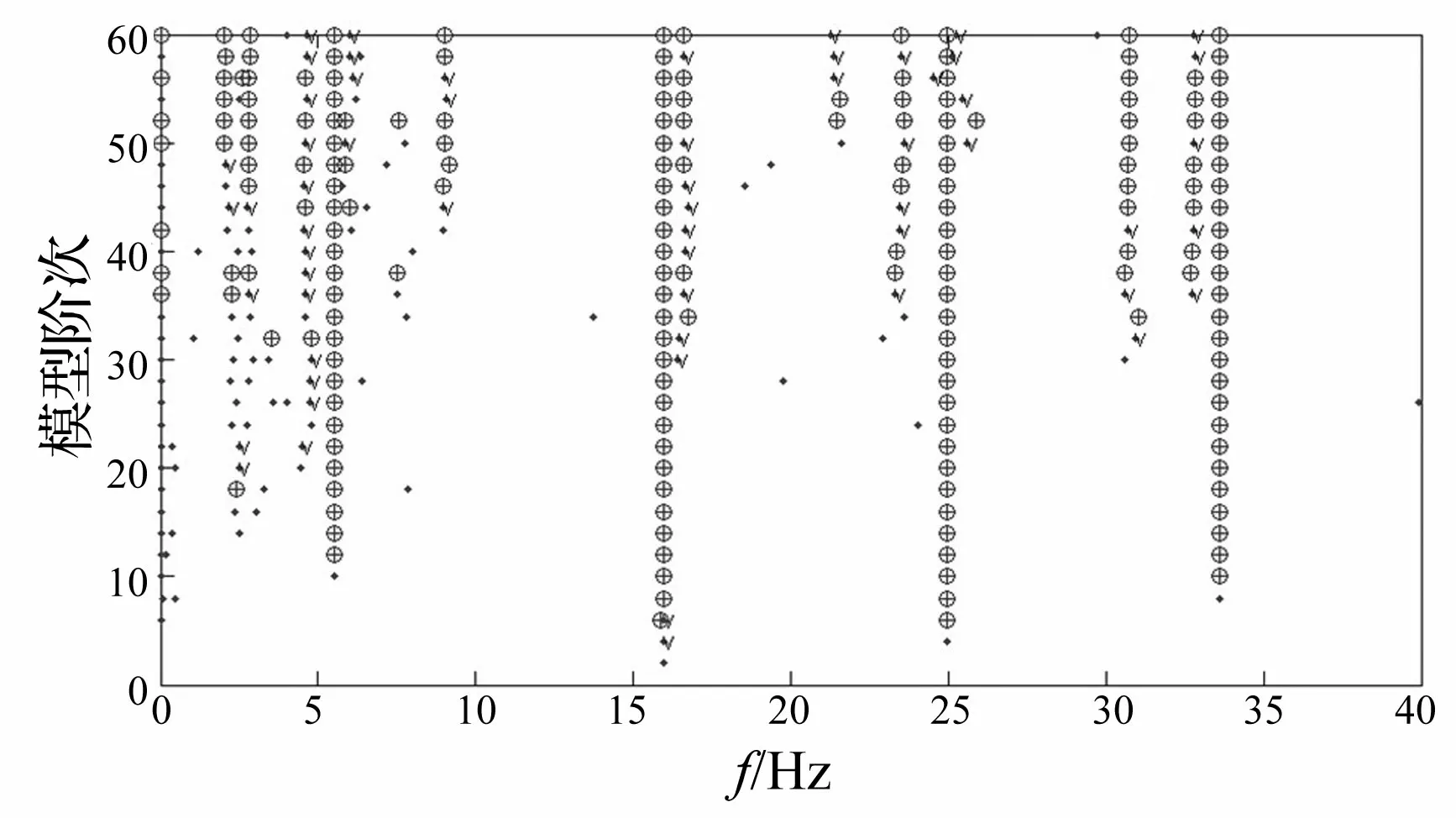
图11 协方差驱动SSI法稳定图

表3 环境激励下改进 ITD法的频率识别值比较(Hz)

表4 环境激励下改进ITD法的阻尼比识别值比较

从表3与表4可以看出，与ITD法相比，改进的ITD法明显提高了对频率和阻尼比等结构模态参数的识别精度。三种识别方法对频率是可以做到可靠识别，阻尼的作用机理很复杂，一般理论值只是对结构的阻尼作了近似的假设，通过试验识别第一阶阻尼比在1%左右。

Toeplitz矩阵中的数据可以作为ITD法的输入数据，这样不再需要采用随机减量法或者自然激励技术(NExT法)进行前处理，从而避免了两种前处理方法的不准确性带来的误差。改进的ITD法的辨识计算时间约为SSI法计算时间的50%，当输出信号较多时，这种优势更明显。从而可见，基于随机子空间法对ITD法进行改进后，精度没有降低，同时缩短了计算时间，这将为该方法应用到结构的实时监测提供了可能。

图12 环境激励下改进ITD法拟合值与输入数据比较

用求得的振型矩阵来反推原始数据，求得的拟合数据与原始数据对比图如图12所示。可以看出：求得的拟合数据与原始相应数据拟合度非常高，进一步证明了改进的ITD法所识别模态参数的准确性和识别方法的正确性。图13为该框架结构辨识出的四阶模态振型。由于将实测结果对理论计算模型进行反馈修正，使得理论模型基本能反映真实情况，固有频率和模态振型辨识结果均与有限元计算分析结构具有良好的一致性。

图13 结构的四阶模态振型辨识结果

4 结 论

基于环境激励下的模态参数识别，不需要专门的外界激励，而且不影响结构的正常使用。运用ITD法进行参数识别时必须先采用随机减量法或者自然激励技术(NExT法)得到数据的自由衰减曲线，而此过程会产生一定的误差，且这两种前处理方法的输出长度的取值方面有一定的人为主观影响，有时也会使得衰减曲线产生偏差，因此采用ITD法进行参数识别必然会产生误差。

(1)基于随机子空间算法和ITD 法的原理，提出了环境激励下结构模态参数识别的改进ITD法。通过数值计算和实验验证了改进ITD对模态参数识别的可行性，与ITD法相比，改进的ITD法明显提高了对结构模态参数的识别精度。

(2)改进ITD 法的计算结果的精度不比SSI法的计算结果的精度差，有时比SSI法的计算精度要高。同时改进ITD 法的计算时间要比SSI法的计算时间要短得多。当输出信号较多时，这种优势更明显。

(3)用求得的振型矩阵阵反推原始数据，求得的拟合数据与原始相应数据拟合度非常高，从而进一步证明了改进ITD法识别模态参数的准确性和识别方法的正确性。

参 考 文 献

[1]Juang J N. Applied system identification[M]. Englewood Cliffs, New Jersey：Prentice-Hall Inc, 1994.

[2]张之颖,谭高铭,吕西林. 环境激励下房屋建筑阻尼比的识别方法[J].西安建筑科技大学学报(自然科学版),2007,39(6):767-772.

ZHANG Zhi-ying,TAN Gao-ming, LÜ Xi-lin. Study on the identification method of damping for the building under ambient excitation[J]. Xi’an Univ. of Arch. & Tech.(Natural Science Edition), 2007,39(6):767-772.

[3]任伟新. 环境振动系统识别方法的比较分析[J].福州大学学报(自然科学版),2001,29(6):80-86.

REN Wei-xin. Comparison of system identification methods using ambient vibration measurements[J]. Journal of Fuzhou University(Natural Science Edition), 2001,29(6):80-86.

[4]徐 良,江见鲸,过静珺. 随机子空间识别在悬索桥实验模态分析中的应用[J].工程力学，2002,19(4)：46-49.

XU Liang, JIANG Jian-jing, GUO Jing-jun. Application of stochastic subspace method to experimental modal analysis of suspension bridges[J]. Engineering Mechanics, 2002,19(4)：46-49.

[5]章国稳,汤宝平,孟利波.基于特征值分解的随机子空间算法研究. [J].振动与冲击，2012，31(7)：74-78.

ZHANG Guo-wen,TANG Bao-ping,MENG Li-bo. Improved stochastic subspace identification algorithm based on eigendecomposition[J]. Journal of Vibration and Shock. 2012，31(7)：74-78.

[6]Koh C G, Hong B, Liaw C Y. Substructural and progressive structural identification methods[J].Engineering Structares.2003， 25(12):1551-1563.

[7]崔 飞. 桥梁参数识别与承载力评估[D]. 上海：同济大学，2003.

[8]姜 浩,郭学东,杨焕龙. 环境激励下桥梁结构模态参数识别的方法研究[J]. 振动与冲击.2008,27(11):126-128.

JIANG Hao, GUO Xue-dong, YANG Huang-long. Research on modal parameters identification of bridge structure under ambient excitation[J]. Journal of Vibration and Shock. 2008,27(11):126-128.

[9]纪晓东，钱稼茹，徐龙河. 模拟环境激励下结构模态参数识别试验研究[J]. 清华大学学报，2006,46(6):669-772.

JI Xiao-dong, QIAN Jia-ru, XU Long-he. Experimental study of modal parameter identification in a simulated ambient-excited structure[J]. J Tsinghua Univ(Sci &Tech), 2006,46(6):669-772.

[10]李海龙. 环境激励下结构模态参数识别方法研究[D]. 重庆：重庆大学，2012.