基于SBFEM的竖向地震重力坝动水压力算法研究

王 毅， 林 皋， 胡志强

(大连理工大学 建设工程学部，辽宁 大连 116024)

坝水相互作用问题一直以来都是研究的重点，从20世纪30年代开始，许多学者都致力于对坝水动力相互作用的研究。Westergaard[1]最早推导了动水压力的经典附加质量理论公式，为地震作用下动水压力的研究做出了开创性的工作。20世纪50年代，有限元方法的发展，对坝水相互作用问题的研究起到了极大的推动作用，其中最为著名的就是以Chopra等[2-5]在对重力坝以及拱坝的坝水动力相互作用进行了比较完善的研究。随后又有学者通过边界元[6-7]或者边界元与有限元耦合的方法[8]来求解坝水相互作用问题。Bouaanani 等[9-10]采用解析的方法得到了能够考虑库水的压缩性以及库底吸收的频域重力坝动水压力求解公式。

随着数值计算方法的不断发展，一种新的半解析数值方法-比例边界有限元方法(SBFEM)脱颖而出，由于其在处理无限域波动问题中存在的极大的优势，大大促进了坝水相互作用问题的研究。林皋等[11-15]最早开展了SBFEM对坝水相互作用的研究，全面考虑库水可压缩性、水库边界吸收等因素以及顺河向、横河向与竖向地震动作用对拱坝、重力坝的水动力相互作用的影响。SBFEM使很多复杂的坝水相互作用问题的计算在很大程度上得以简化，并从频域分析发展到时域分析，均取得了较好的效果。王翔等[16-18]采用比例边界有限元方法推导了二维高阶双渐进透射边界条件，并应用在求解大坝库水相互作用中。李上明[19]采用比例边界有限元方法与有限元相结合的方法分析了瞬态坝库耦合问题。

先前的理论大多忽略了竖向地震动对重力坝动水压力的影响，往往只是考虑了顺河向的地震动激励对其的影响，Chakrabarti等[20]给出了竖向地震动的影响，但是其仅仅是考虑了库水的可压缩性。著名学者Chopra[21]对Westergaard公式进行了适用性讨论并加以改进，而且还推导了竖向地震动激励情况下坝面动水压力的解析公式，讨论了竖向地震动激励对坝面动水压力的影响。

本文在比例边界有限元的体系下，重点讨论竖向地震动激励对动水压力响应的影响，不仅能够考虑库水的可压缩性还能够模拟库底的吸收作用，而且实现了动水压力的频域和时域求解。

1 基于比例边界有限元方法的动水压力基本理论

在地震动作用下，考虑水体的可压缩性，假设水体为小扰动无黏性液体，整个水域应满足Helmholtz方程

(1)

式中：p表示动水压力，2为Laplace算子，上标“··”表示对时间的二阶导数，c为水中压力波波速，忽略库水的可压缩性，c值就为无穷大，方程(1)退化为标准的Laplace方程，在考虑水的可压缩性的时候，c值取为1 440 m/s。

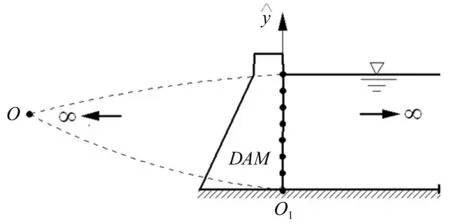
图1 坝水系统示意图

在坝水交界面上满足应力连续性边界条件：

(2)

为了考虑库底的柔性影响，采用Hall等[22]提出的一维吸收边界条件：

(3)

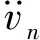
在无穷远处满足辐射条件：

(4)

本文采用SBFEM算法，由于仅存在坝水交界面的离散边界，无穷远处的边界不需要离散，因此能够自动满足无穷远处的辐射条件，在计算中不需要对此边界进行特殊处理。

库水表面，忽略微幅重力波的作用，此时库水表面的动水压力为零。

在比例边界有限元的框架下，可以把相似中心O选择在坝体的下游无穷远的地方(如图1所示O)，此时可以认为水库的上下表面是平行的关系，从而只需离散坝水交界面上的节点，从而大大的减少了计算量，得到整个求解域上的关于动水压力的积分弱形式。

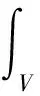
(5)

通过对积分弱形式的进一步的处理，可以得到在比例边界有限元框架下的控制方程和边界条件，积分域V表示整个水域，积分域S表示水库的各个边界面，w表示积分权函数。文献[14]给出了其详细的推导过程及其求解过程，坝面动水压力的频域结果表示为

(6)

其中的各个矩阵变量的含义以及求解方法都在都在文献[14]中有详细的求解方法。

为了便于下文的应用，此处需要对频域动水压力进行整理，把顺河向与竖直向地震动加速度激励写成一个列向量，p可以表示为

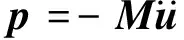
(7)

(8)

因此，坝面上所承受的压力在仅受到竖直向地震动激励时

(9)

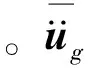
2 时域求解

考虑到坝水系统的线性假设，可以对频域的计算结果进行一次傅里叶逆变换(FFT)就能够得到时域的结果。具体操作步骤如下：

(10)

3 数值算例

(11)

式中：w为单位水重，g为重力加速度，H为坝前水深，y为坝体迎水面竖向坐标，c为水中波速，本文取为1 440 m/s。

图2 重力坝计算模型[14]

3.1 频域结果

3.1.1 激励频率影响

忽略库底的吸收作用，采用本文方法可以得到坝踵处竖向地震动激励的动水压力频响曲线

如图3所示，横坐标表示无量纲激励频率，其中ω1为水库的一阶自振频率(ω1=πc/2H)；纵坐标表示频域动水压力与静水压力的无量纲比值的绝对值。结果表明，采用本文方法与解析解吻合良好，即使是在水库的前三阶自振频率点附近，仍然能够得到具有较高精度的结果。另外，计算结果表明，对坝踵的动水压力影响较大的频率区间在水库的一阶自振频率之内以及水库的各阶自振频率附近的相对较小带宽的频率区域。不考虑库底的吸收作用，在激励频率达到水库的各阶自振频率时，坝面上的动水压力也将出现峰值，表明坝水系统的无阻尼共振特性。当激励频率超过水库的一阶自振频率之后，动水压力响应也急剧下降，尤其是激励频率在水库的两阶自振频率之间的时，坝水响应趋于零，其与解析解表达相吻合。

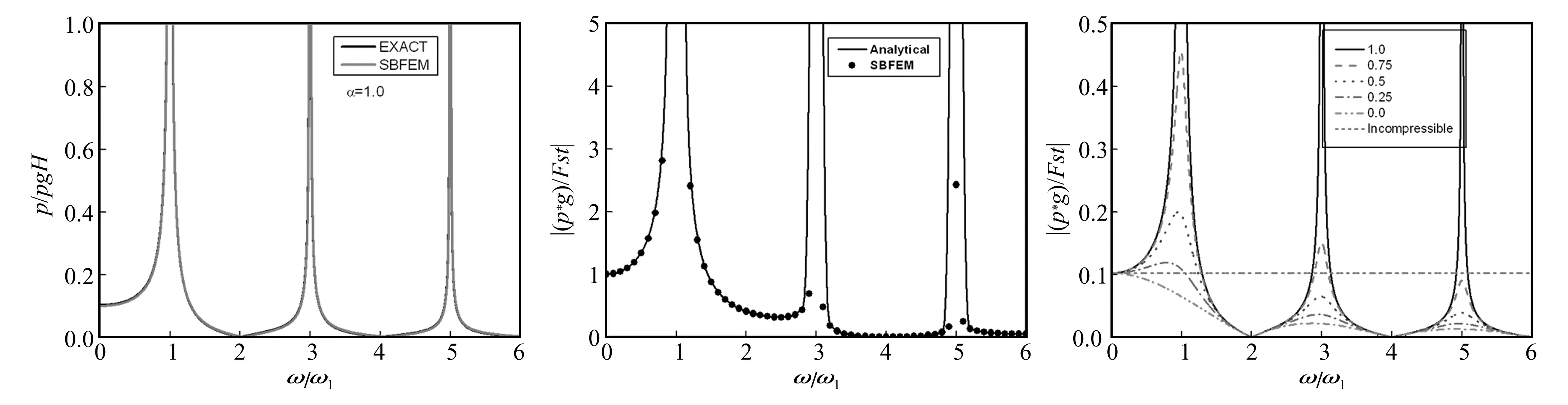
图3 坝踵处动水压力频响曲线

为了更加直观的表示竖向动水压力对整个坝面的作用，图4给出了坝面整体动水压力的频响曲线。横坐标仍为无量纲频率，纵坐标为坝体表面在受到竖向地震动激励情况下的总体动水压力，解析解仍为文献[21]所给出的

(12)

式中:H(Ω)为整个坝面上的动水压力，求解时需要在迎水面进行积分；F0=ρgH2/2，为坝面上的静水压力；Ω=ω/ω1，无量纲激励频率。

图4能够清晰的表示出整个坝面在竖向动水压力的作用下的响应情况：① 在水库的各阶自振频率点，动水压力响应存在相同的共振现象；② 动水压力响应的敏感频率区间在库水的二阶自振频率以内，与坝踵处的频响函数相比，在水库前两阶自振频率之间，动水压力响应有了显著的增大，原因在于坝体迎水面上的其他部位对其的贡献得到了累加；③ 动水压力响应在水库二阶自振频率之后急剧减小，逼近于零点，表明整个坝面的响应都与坝踵处相差不大，仅在库水的高阶自振频率点附近一个较小的窄带宽内存在一定的共振响应值，同时由于共振峰值的存在，本文计算结果与解析解之间在此点附近也存在一定的差异。

3.1.2 库底阻尼对坝水相互作用的影响

图3和图4的计算结果都是在忽略阻尼的情况下得到的理想意义的解。事实上，坝水系统也是存在阻尼的，尤其是库底的淤沙，对地震波有明显的吸收作用。本文采用库底反射系数的方法来模拟库底的阻尼，通过选择不同的反射系数来表示库底淤沙的阻尼作用，如图5所示。随着反射系数的降低，库底的吸收作用愈加明显，尤其是在水库的自振频率点处，峰值被明显削弱。当库底为完全柔性的情况下，坝水相互作用的频域特征几乎完全被改变，在整个频率范围之内，响应值都处于一个较低的水平，尤其是在ω<2ω1的频率区间内，响应几乎呈线性下降趋势，完全改变了刚性库底在水库的第一阶自振频率处出现峰值的特性，此外，完全柔性库底仍然保留了坝水相互作用在两阶自振频率中点处的驻值现象。动水压力峰值也随着反射系数的减低而逐渐降低，而且随着激励频率的增大，坝踵处的动水压力峰值也存在下降的趋势，但衰减趋势并不明显，这与垂直激励下关于动水压力的加速度脉冲响应函数并不衰减[21]密切相关。综上所述，库底阻尼对坝水系统的动水压力响应起着至关重要的作用，在实际工程应用中可根据库底的实际情况对库区的阻尼进行估计。

3.1.3 水的可压缩性的影响

以上算例都是在考虑了库水的可压缩性得到的结果，事实上，在相当长的一段时间内，都是忽略水的可压缩性来求解坝水系统的动力响应的。不考虑水的可压缩性，整个水库的水体控制方程将退化为Laplace方程，从而导致系统的反应将与频率无关，在频响曲线上将会是一条平行于频率轴的直线，其初值是以上各个算例得到的初值，即在ω=0处的响应值(如图5所示)。当库底的反射系数大于0.25时，水的可压缩性在库水一阶自振频率以内显著增大了坝面上的动水压力，相反在高频阶段，其仅在库水的自振频率附近的较小频率域内能够提高坝面上的动水压力，而且随着频率的不断增大，这种作用也在逐渐降低。如若库底的反射系数小于0.25时，忽略库水的可压缩性就在整个频率范围内较大的估计了在竖向地震动激励下坝面上的动水压力。在同时考虑库水的可压缩性以及库底的吸收作用所得到的效果与现行工程中所采用的不可压缩库水所得效果不尽相当，在库底条件相对较柔的情况下，即反射系数小于0.5时，前者所得的计算结果要明显小于后者；而当库底相对刚性情况下，即反射系数大于0.5，库底淤沙层较薄时，前者计算结果在水库的一阶自振频率之内要远远高于后者。

3.2 时域结果

以上给出的计算结果均为频域结果，在大坝遭受地震作用下，各个时刻的坝面上的动水压力往往是我们关注的重点问题，这就要求能够在时域中求解坝面上的动水压力，从而确定在整个地震过程中的最不利时刻。

为了更好地与解析解进行比较，本文选取比较具有代表性的三角形脉冲加速度时称曲线。脉冲激励的时长为2 s，峰值为1 m/s2。为了便于比较，本文还给出了在大坝受到水平方向上相同的地震动激励下，坝面动水压力的变化情况。

图6 三角形脉冲加速度

计算结果表明，水平向结果图7和竖向结果图8与解析解吻合良好。比较水平向与竖向时域结果的峰值，假设大坝在水平与竖向收到相同的地震加速度的激励，发现大坝坝踵处的动水压力接近静水压力的8%，而竖向情况下则超过11%。在竖向激励情况得到的峰值比水平向激励情况下更大。除了近场地震动之外，一般竖向地震动加速度小于水平相的地震加速度。假设av=(2/3)ah时，两者在坝踵处的动水压力也比较接近。因此，竖向激励是一个不可忽略的影响，不考虑竖向地震动的影响会明显低估坝面在地震过程中受到的动水压力。此外计算结果表明，动水压力的时程形式与激励的形式基本吻合，尤其是在坝体受到顺河向激励的情况下。在坝体受到竖向激励时候，在整个时程上，动水压力会出现较小幅度的振荡，如图8所示。

4 结 论

通过对竖向地震动激励对坝面动水压力的研究，不难做出以下论点：

(1)竖向地震动激励对大坝的考虑水库边界吸收影响时，竖向动水压力与水平动水压力存在一定的相位差，地震响应的影响是不可忽略的。频域结果和时域结果均表明竖向地震动引起的坝面动水压力在本文假设模型下不亚于同等幅值地震动激励下的顺河向结果，但由于垂直激励下动水压力响应与边界条件、淤沙本构等有很大关系，使得此项响应值在实测、实验和数值计算结果上存在一定的差异。因此，在进行大坝-库水系统的动力分析中应该对竖向地震动激励以足够的重视。

(2)水的可压缩性对坝体-库水系统的影响随着激励频率和库底反射系数的变化呈现出不同的特性，采用简单的不可压缩库水假设在处理坝水相互作用问题上具有明显的局限性。

(3)库底的柔性作用对地震波的吸收效果显著，合理地确定库底的反射系数能够更加真实地反映坝水相互作用问题中淤沙层的吸能效应。此外，反射系数法能够更加方便地体现库底的不同的淤沙条件。

(4)采用比例边界有限元方法对竖向地震动激励下坝面动水压力的计算仅需要离散坝面单元，计算量较之有限元方法有大幅度的降低，而且对于无穷远处的辐射条件能够较好的模拟，计算结果精度较高，适合推广应用于三维拱坝的计算中。

参 考 文 献

[1]Westergaard H M. Water pressures on dams during earthquakes [J]. Transactions (ASCE),1933, 98:418-433.

[2]Chakrabarti P, Chopra A K. Hydrodynamic effects in earthquake response of gravity dams [J]. Journal of the Structural Division, 1974, 100(s16):1211-1224.

[3]Porter C S, Chopra A K. Dynamic analysis of simple arch dams including hydrodynamic interaction [J]. Earthquake Engineering and Structural Dynamics, 1981,9(6):573-597.

[4]Porter C S, Chopra A K. Hydrodynamic effects in dynamic-response of simple arch dams [J]. Earthquake Engineering and Structural Dynamics, 1982,10(3):417-431.

[5]Hall J F, Chopra A K. Dynamic analysis of arch dams including hydrodynamic effects [J]. Journal of Engineering Mechanics (ASCE), 1983,109(1):149-167.

[6]Hanna Y G, Humar J L. Boundary element analysis of fluid domain [J]. Journal of Engineering Mechanics Division (ASCE),1982; 108(2):436-450.

[7]Humar J L, Jablonski A M. Boundary element reservoir model for seismic analysis of gravity dams [J]. Earthquake Engineering and Structural Dynamics, 1988, 16(8):1129-1156.

[8]Estorff O V, Antes H. On FEM-BEM coupling for fluid-structure interaction analyses in the time domain [J]. International Journal for Numerical Method in Engineering, 1991, 31(6):1151-1168.

[9]Bouaanani N, Paultre P, Proulx J. A closed-form formulation for earthquake-induced hydrodynamic pressure on gravity dams [J]. Journal of Sound and Vibration,2003, 261:573-582.

[10]Bouaanani N. Miquel B. A new formulation and error analysis for vibrating dam-reservoir systems with upstream transmitting boundary conditions [J]. Journal of Sound and Vibration, 2010,329：1924-1953.

[11]林 皋, 杜建国. 基于SBFEM的坝-库水相互作用分析[J]. 大连理工大学学报, 2005,45(5):723-729.

LIN Gao, DU Jian-guo. Analysis of dam-reservoir interaction based on SBFEM[J]. Journal of Dalian University of Technology, 2005,45(5):723-729.

[12]Lin G, Wang Y, Hu Z. Hydrodynamic pressure on arch dam and gravity dam including absorption effect of reservoir sediments [J]. IOP Conf. Series：Materials Science and Engineering,2010, 10(1)：012234.

[13]Lin G, Du J, Hu Z. Dynamic dam-reservoir interaction analysis including effect of reservoir boundary absorption [J]. Science in China Series E Technological Sciences, 2007, 50(1);1-10.

[14]Lin G, Wang Y, Hu Z Q. An efficient approach for frequency-domain and time-domain hydrodynamic analysis of dam-reservoir systems [J]. Earthquake Engineering and Structure Dynamics, 2012,41(7):1725-1749.

[15]杜建国，林 皋，谢清粮.一种新的求解坝面动水压力的半解析方法[J]. 振动与冲击,2008，27(3):31-34,45.

DU Jian-guo, LIN Gao, Xie Qing-liang. A new semi-analytical method for solving hydrodynamic pressure on dams[J]. Journal of Vibration and Shock,2008，27(3):31-34,45.

[16]王 翔, 金 峰. 动水压力波高阶双渐进时域平面透射边界I：理论推导[J]. 水利学报,2011, 42(7)：839-847.

WANG Xiang, JIN Feng. High-order doubly asymptotic time-domain plane transmitting boundary for hydrodynamic pressure I. Theoretical derivation[J]. Journal of Hydraulic Engineering, 2011, 42(7)：839-847.

[17]王 翔, 金 峰. 动水压力波高阶双渐进时域平面透射边界II：计算性能[J]. 水利学报,2011, 42(8)：986-993.

WANG Xiang, JIN Feng. High-order doubly asymptotic time-domain plane transmitting boundary for hydrodynamic pressure II. Computational performance[J]. Journal of Hydraulic Engineering, 2011,42(8):986-993.

[18]Wang X, Jin F, Prempramote S, et al. Time-domain analysis of gravity dam-reservoir interaction using high-order doubly asymptotic open boundary [J]. Computers and Structures, 2011,89(7-8):668-683.

[19]李上明. 基于比例边界有限元法的坝库瞬态耦合分析[J]. 华中科技大学学报(自然科学版),2011,39(9):108-111.

LI Shang-ming. Dam-reservoir transient coupling analysis based on SBFEM[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(9):108-111.

[20]Chakrabarti P, Chopra A K. Hydrodynamic pressures and response of gravity dams to vertical earthquake component [J]. Earthquake Engineering and Structural Dynamics, 1972,1(4):325-335.

[21]Chopra A K. Hydrodynamic pressures on dams during earthquakes [J]. Journal of the Engineering Mechanics Division, Proceeding of the American Society of Civil Engineers, 1967,93(EM6):205-223.

[22]Hall J F, Chopra A K. Two-dimensional dynamic analysis of concrete gravity dams and embankment dams including hydrodynamic effects[J]. Earthquake Engineering and Structural Dynamics, 1982, 10(2), 305-332.